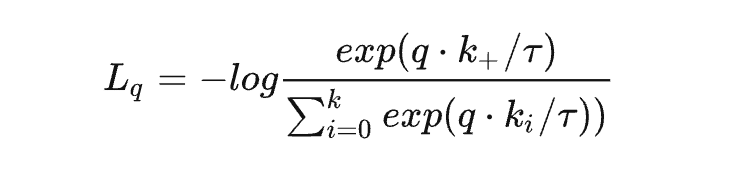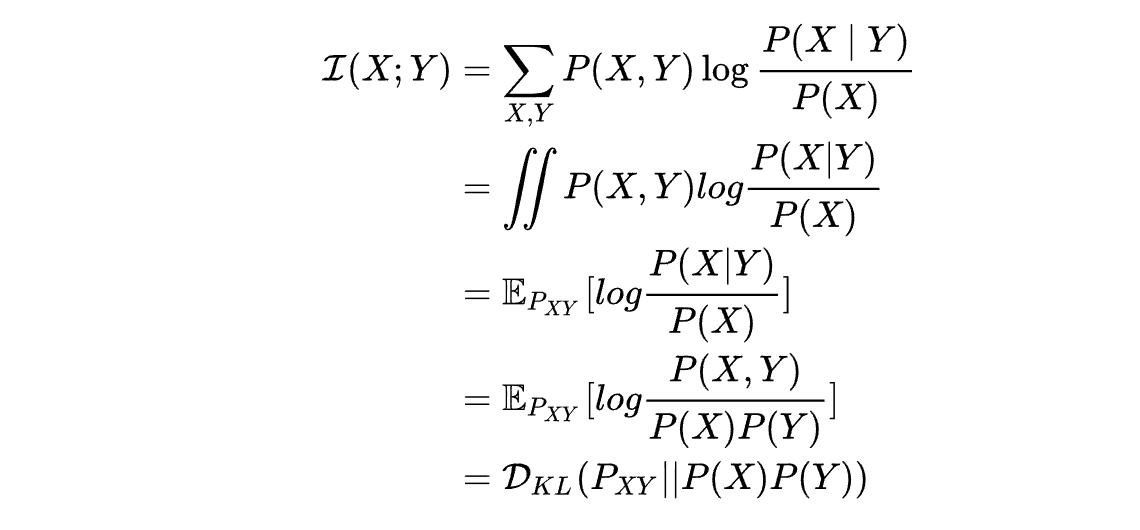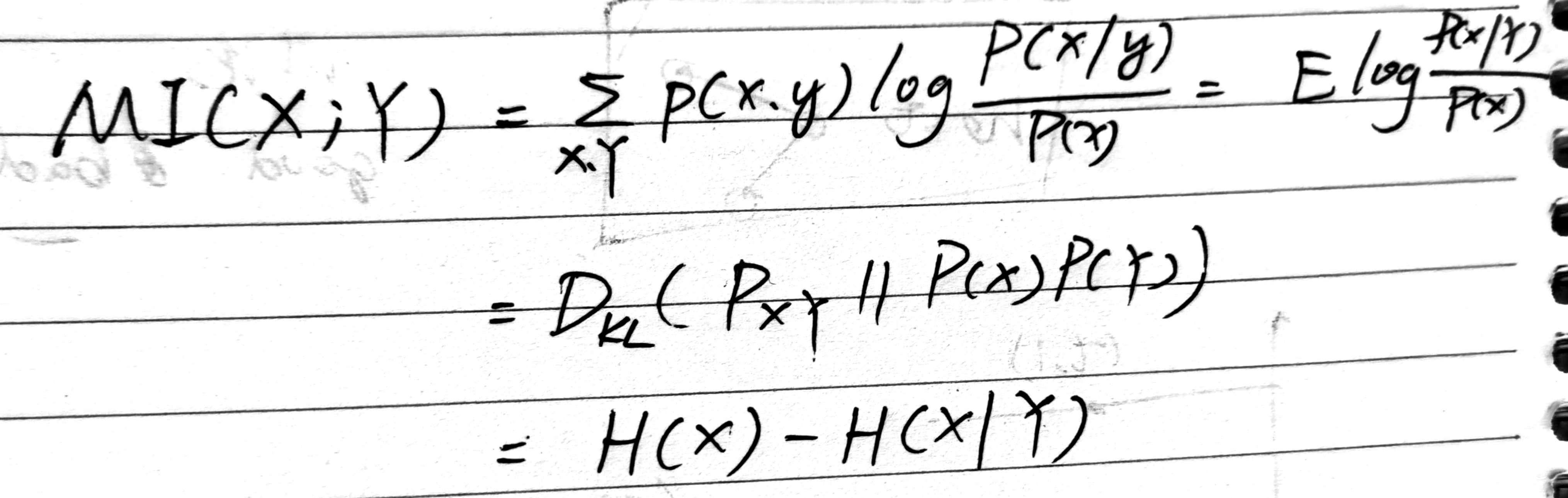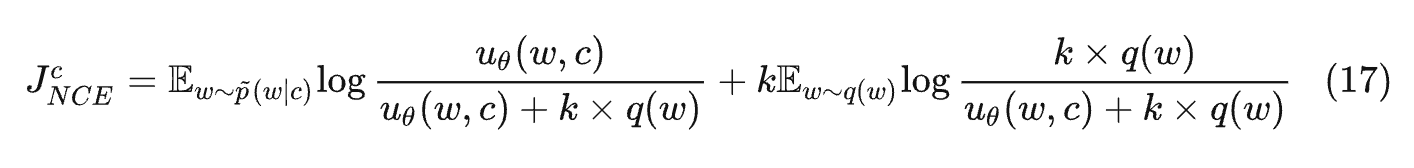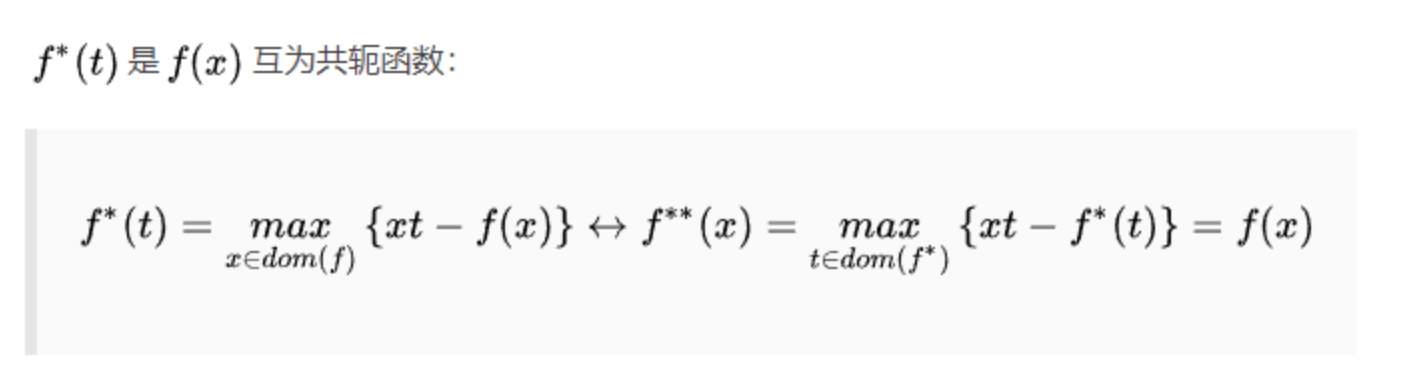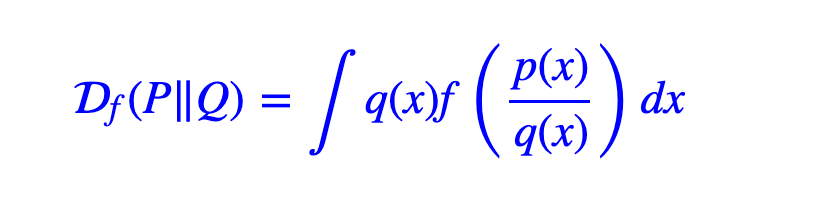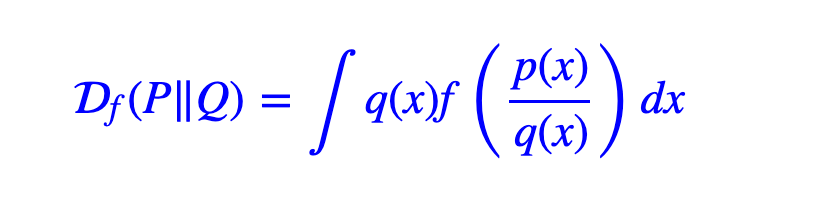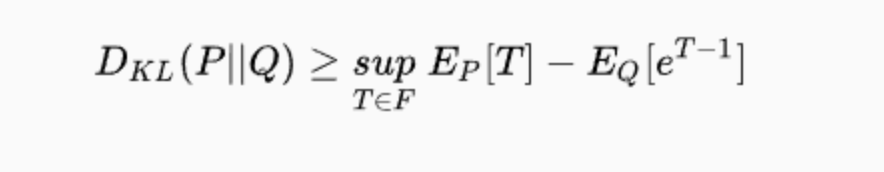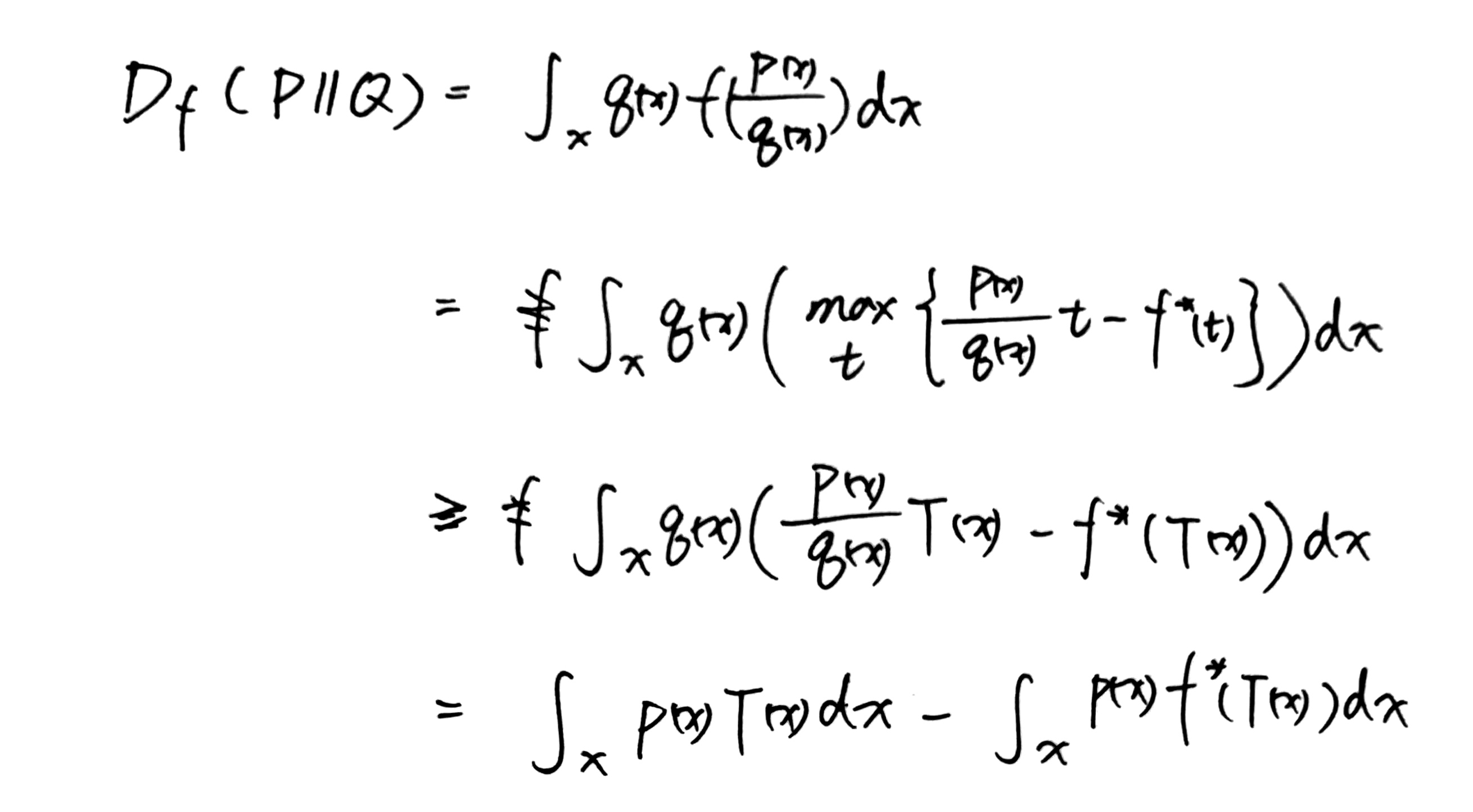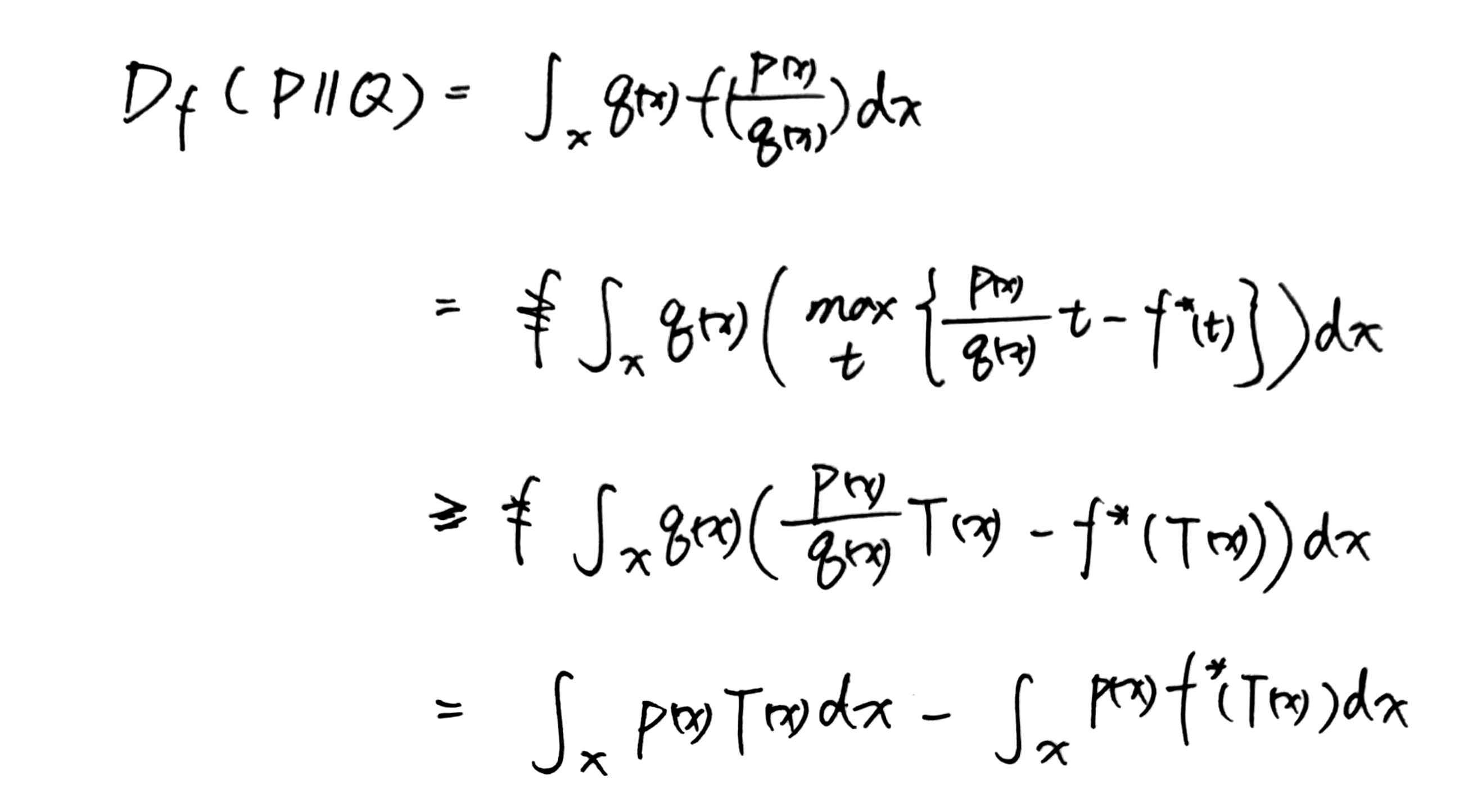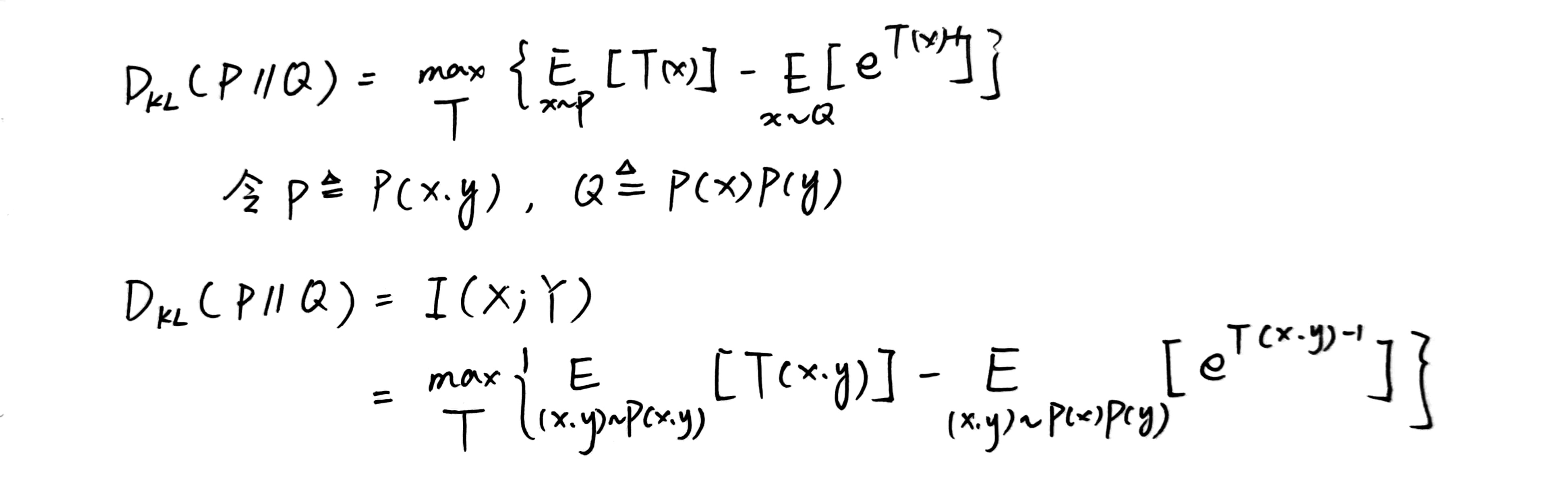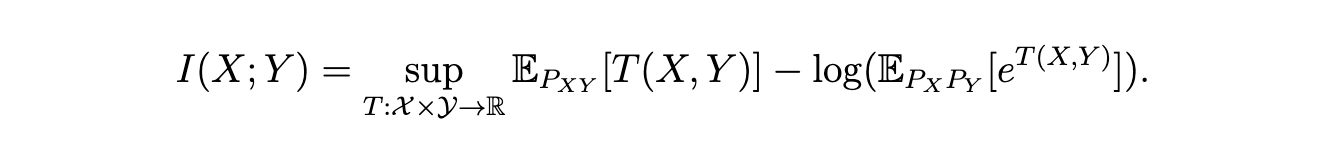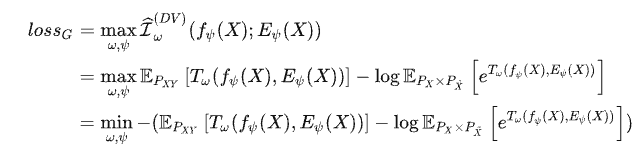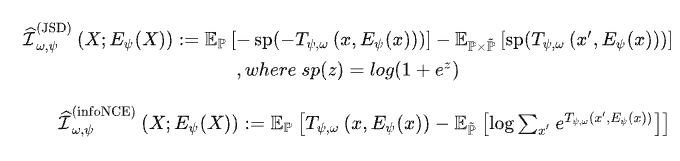一次组内的技术分享,没有什么涉密内容,记录下来方便以后回顾,也可以分享给有需要的朋友一起讨论。
Warning
- 很多内容是自己总结出来的,不保证正确性。
- heavy math!
- 对于大家日常工作应用作用可能不是特别大。
内容安排
- 问题引出:5~10分钟
- 数学推导:20分钟(能力有限,这段可能讲不清楚,不需要的同学可以关注问题与最后的结论)
- 回到目标问题:5~10分钟
- 推广到其他问题:10分钟
- 总结:5分钟
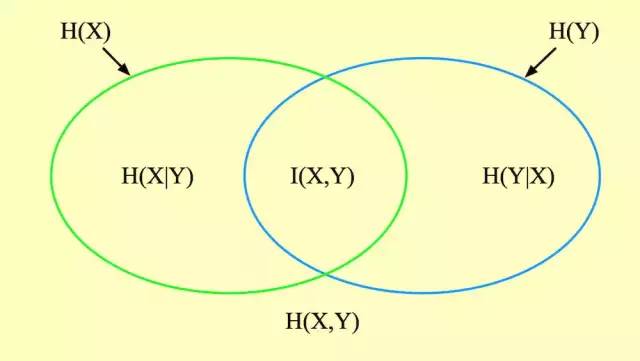
互信息
从对比学习 loss 形态开始谈起
概念与问题定义
对比学习常见的loss,但是为什么是这样?
比如softmax或者lr这样的模型,其问题假设与目标存在清晰的推导关系。即,为什么使用这样的激活,这样的loss函数,最终我们都能在GLM理论中找到依据。
正例比较近,负例比较远,那这个呢(refer DGI;2019 ICLR)?
L = 1 m Σ i = 0 m [ l o g T ( x i , y i ) − Σ j = 0 K l o g ( 1 − T ( x i , y j ) ) ] L=\frac{1}{m}\Sigma_{i=0}^m[logT(x_i,y_i)-\Sigma_{j=0}^Klog(1-{T(x_i,y_j)})] L=m1Σi=0m[logT(xi,yi)−Σj=0Klog(1−T(xi,yj))]
概念与问题定义
线索:
概念与问题定义
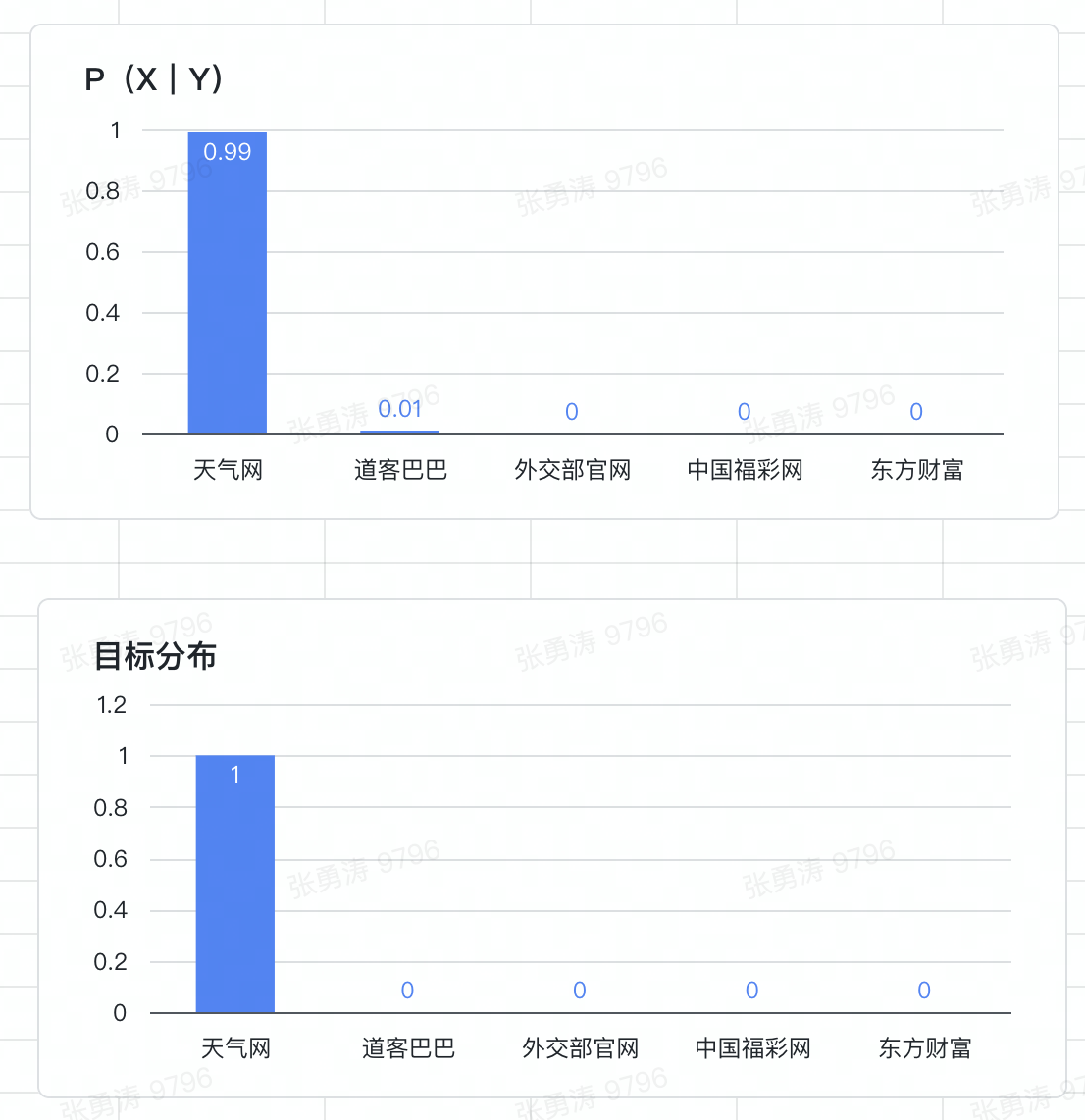
先明确互信息的物理意义,我们暂且用点击数据举例子。
其中 X 是站点,Y是Query。
概念与问题定义
如何计算(1): CrossEntropy
- 没有直接刻画先验分布(一个C可能有多个正例X),但是可以在训练数据分布中体现出来
- 计算复杂性:Vocab非常大。
如何计算(2): Noise Contrastive Estimation
可以参考 Noise Contrastive Estimation 前世今生——从 NCE 到 InfoNCE
通过最大化同一个目标函数来估计模型参数 和归一化常数,NCE 的核心思想就是通过学习数据分布样本和噪声分布样本之间的区别,从而发现数据中的一些特性.
如何计算:互信息估计器
方法3: MINE
难点:有时我们最多只知道其中一个概率分布的解析形式,另外一个分布只有采样出来的样本,甚至很多情况下我们两个分布都不知道,只有对应的样本(也就是说要比较两批样本之间的相似性)
有的函数写不出解析式,有的函数有解析式,但是非常不好算。互信息就属于这一种情况。
警告
(接下来数学含量有些高,尽量用5分钟说明白,但是不太可能,但是最后我会给出一个结论)
如何计算:屠龙刀——凸共轭
数学大佬们的工具箱里提供了一个很好的锤子来敲这个问题。
一定要注意,这个过程中,我们是换了一个自变量,这个新的自变量是旧的自变量的函数。
一个很棒的特点是,我们可以针对某个具体的点进行估计。
如何计算:屠龙刀——凸共轭
一个很棒的特点是,我们可以针对某个具体的点进行估计。
估计法的好处:可以对某个点去逼近指定的期望,不依赖状态数。(RL中传统方法更多的使用DP,复杂问题在nn时代更多的使用MC就是这个原因。)
注意:对于常见的凸函数f,我们可以精确计算出其凸共轭函数。
如何计算:倚天剑——f散度
为了方便理解,先举一个简单的例子:闵氏距离
如何计算:倚天剑——f散度
f-散度是对KL散度的一般化,同样是对两个分布的差异的测度。
如何计算:倚天剑——f散度
f需要满足:
- 它们都是非负实数到实数的映射(ℝ∗→ℝ);
- f(1)=0;
- 它们都是凸函数。
如何计算:倚天剑+屠龙刀 = 九阴真经
最后一步,把两个小工具组合起来,我们会得到一个很有用的工具:互信息下界估计器。
如何计算:九阴真经——互信息下界估计
对 f 散度内部的 f 函数转化为共轭函数。
如何计算:九阴真经——互信息下界估计
第一行:互信息的f散度表示方式
如何计算:九阴真经——互信息下界估计
第二行:利用共轭变换,并引入变量t。
如何计算:九阴真经——互信息下界估计
第三行:去掉max,并且把T表示为原始变量的函数。
第四行:简单数学变形。
如何计算:九阴真经——互信息下界估计
最终我们迎来了终点:
如何计算:变分估计
回忆 Page6 的一个变换:P、Q的互信息等价于PQ的独立分布和联合分布的KL散度。
其中,T是任意函数(这里我们会用神经网络来取代这个T,但也要注意,神经网络不是“任意函数”,不同的网络结构会影响下界的逼近程度,或者说,效果)。
Donsker-Varadhan表示
单看公式,比之前的下界估计公式只是多了一个log,我们在这里不深究其无偏性了,只需要知道,这里给了一个更紧的下界。
I ( X ; Y ) = Σ X , Y P ( X , Y ) l o g P ( X ∣ Y ) P ( X ) I(X;Y)=\Sigma_{X,Y}P(X,Y)log\frac{P(X|Y)}{P(X)} I(X;Y)=ΣX,YP(X,Y)logP(X)P(X∣Y)
警告关闭
(警告关闭,回到正常路况)
具体算法
这里是我最接近infonce的地步了,后面还没研究明白(汗):
L = 1 m Σ i = 0 m [ T ( x i , y i ) − l o g Σ j = 0 K e T ( x i , y j ) ] L=\frac{1}{m}\Sigma_{i=0}^m[T(x_i,y_i)-log\Sigma_{j=0}^Ke^{T(x_i,y_j)}] L=m1Σi=0m[T(xi,yi)−logΣj=0KeT(xi,yj)]
局部小结
- 互信息的核心思路在于“区分”,也就是那个T函数,而为了有更好地区分能力,T的输入,通常是embedding,需要学习最有区分能力的表示。
- 很多时候会用作中间层loss、辅助loss,自己单独是一个loss的时候通常以预训练任务的形式出现。(因为其encoder的目的是最大化对输入的表示的可分性,后面会给出具体例子,比如人脸识别、比如BI。)
- 核心思路是最大化P(x|y)/p(x),这个物理意义是点互信息,就是给了Y,最大化对X的区分能力。(后面在例子中会强调这一点。)
应用
知道了这个有什么用呢?
互信息 -> f散度 -> 具体化为某一个散度的对偶下界 -> 参数化下界 -> 抬高下界
所以优化 T 判别器帮助我们找到最好的下界最大值;优化x、y可能存在的对应的encoder才是真正优化这个“不太准”的互信息loss。
I ( X , Y ) > = E P ( X , Y ) [ T θ ( x , y ) − E q ( Y ~ ) [ l o g Σ y ∈ Y ~ e x p T θ ( x , y ~ ) ] ] I(X,Y) >= \mathbb{E}_{P(X,Y)}[T_\theta(x,y) - \mathbb{E}_{q(\widetilde{Y})}[log\Sigma_{y \in \widetilde{Y}}expT_\theta(x,\widetilde{y})]] I(X,Y)>=EP(X,Y)[Tθ(x,y)−Eq(Y )[logΣy∈Y expTθ(x,y )]]
关键是要确定,我们的业务问题中,X和Y是什么?以及对应的网络结构怎么设计来做到更好地归纳偏置。
可以想像,我们要隔着一层塑料薄膜找到一坑洼地的最小值?
- T的输入,也就是输入的encoder的作用是让薄膜尽可能的贴近地面。(比如host的embedding)
- T自身往往会比较简单,通常以内积或者cosine的形式
估计器之间对比
回忆一下,还记得前面的f-散度这个概念吗?我们上面给出了KL散度下界的推导和DV下界的推导。其实,每一个 f 我们都能自行对应出来一个新的互信息下界估计器。
这里只给出最常见的三种:JSD、InfoNCE、DV
估计器之间对比
回忆一下,还记得前面的f-散度这个概念吗?我们上面给出了KL散度下界的推导和DV下界的推导。其实,每一个 f 我们都能自行对应出来一个新的互信息下界估计器。
这里只给出最常见的三种:JSD、InfoNCE、DV
这里也给出了一种解释,为什么负例越多越好。
应用
- 看论文时好理解一些,对 loss 理解更深刻一些。
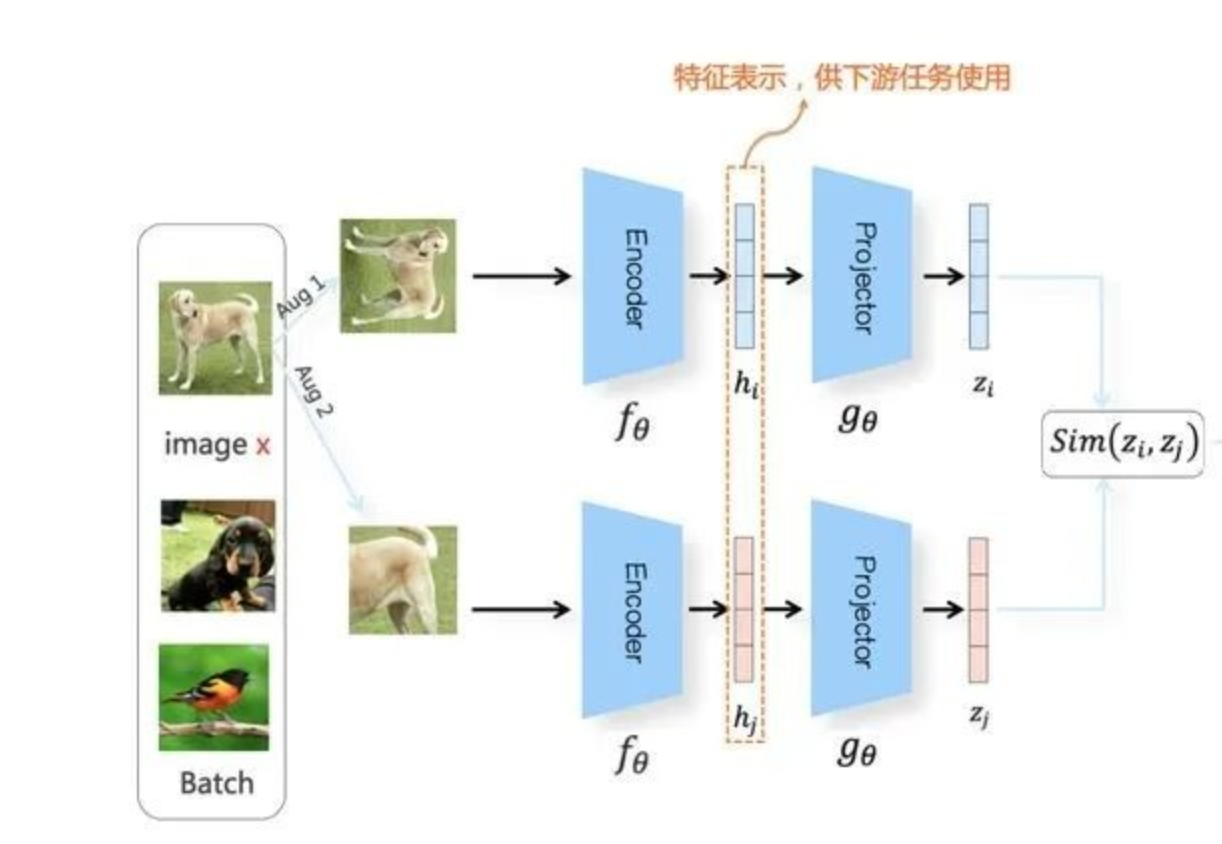
Example1: Moco & SimCLR
- 这里只考虑 Moco v1 和 SimCLR v1
- 整体思路往上面套:需要找一个Q、一个X,因为没有点击数据,所以Q和X都是自己,但是太简单怎么办,Q和X都是同一张图片的不同View。
- 两个工作核心改进点之一都是加大负例,前者是Memory Bank,后者是InBatch
Example2: Deep Infomax
CV领域一个很重要的工作就是如何设计出比较好的图片特征提取器或者压缩器。
(比较老套的)常规思路(不太了解最新业界的工作):
- 大规模分类任务预训练
- AutoEncoder or GAN 等生成模型。
Example2: Deep Infomax
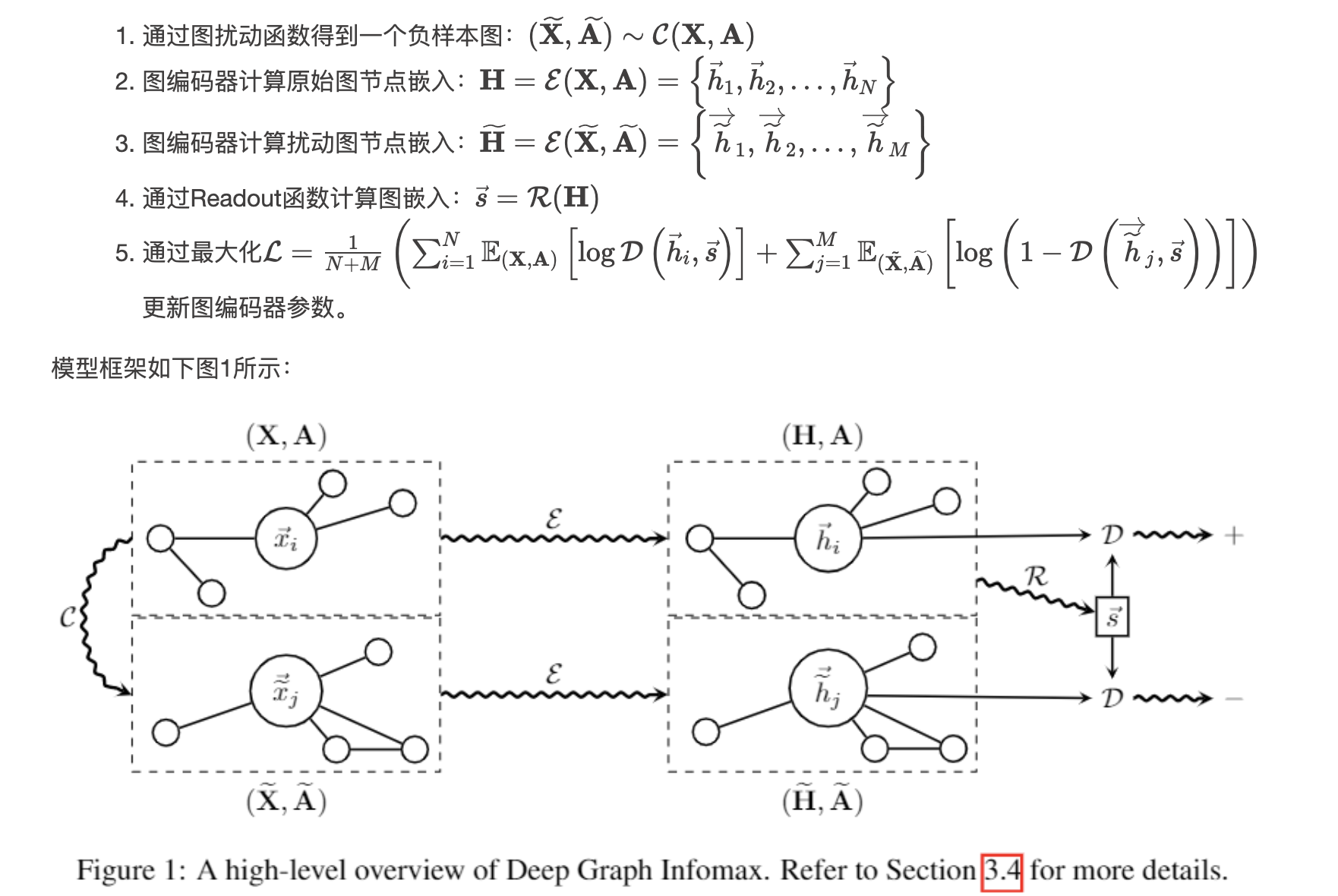
Example3: DGI(2019 ICLR)
其实就是汲取了DIM的思想,将Infomax准则运用到了graph领域中。
扰动方法是:保留原始图邻接矩阵不变,即将特征矩阵X进行随机row-wise shuffle。
Example4: Information Bottleneck
基本思路是,我们只需要量化和最小化神经网络产生的隐藏表征与相应的输入之间的依赖性,但也要量化和最大化同一隐藏表征与输出变量之间的依赖性。我们可以用相互信息量来量化这些信息。
m i n p ( t ∣ x ) I ( X ; T ) − β I ( T ; Y ) min_{p(t|x)}I(X;T)-\beta I(T;Y) minp(t∣x)I(X;T)−βI(T;Y)
举个例子,原始输入是X,中间层是T,label是Y,这个loss核心就是提取Y所必备的信息放在T中,把X中与Y无关的特征抛弃掉。
其中 beta 为拉格朗日乘子, 改变beta,可以让T在尽力保留Y信息与尽量丢掉X的信息之间选择合适的平衡,用信息瓶颈来比喻,T可以比作一个瓶子,将其含有的信息比作水,beta参数规定了瓶子大小的下限,在优化过程中,瓶子不断缩小,水不断被排出,最终瓶子减小到下限,保有的信息量也就收敛了。
Warning 保命
如果不看原始论文直接听我讲有的没的,容易被误导,原始论文就这么点东西。实际上我只是尽可能的往互信息理论上面套,套不上的我都没讲。
总结
我们用 ML 的思路解决一些问题的时候,往往要定义出一些目标函数或损失函数。一些时候,这个目标函数是易于计算的,那自然是方便的。但是有些时候,这个形式是很难以计算的,那怎么办呢?我觉得一般又三种情况:
在数学上或工程上进行良好的设计与化简:比如FM,大规模离散分布随机采样的alias method等,这一点其实即使是形式良好的目标函数,如果我们能做到其实也是要做的。前者场景下是雪中送炭,而后者是锦上添花。
通常是一些分布难以表达的场景。可能会使用蒙特卡洛估计计算期望来替换原始分布的方式,比如NCE(噪声对比估计)等思路。
后退法。也就是说,我们不计算原始损失函数最小化,我们找一个损失函数的下确界,这个下确界越紧致越好,或者我们可以不断提高紧致度。比如EM算法类似今天的方法,直接利用数学工具去优化一个确定的下界(往往更好算)。
Warning 保命
- 这个分享原本是出于做图自监督相关工作的时候碰到的疑问引发的思考,全文内容不敢保证正确性,如有错误欢迎指正或联系我
- 过于关注这个loss框架的话,可能会忽视一些论文中细节却重要的工作。比如DIM中的先验分布设计参考了VAE,不只是互信息最大化。比如SimCLR中的Projector结构的作用,以及最后的度量函数为什么用cosine而不是内积。
- 知道了这个,可以帮助我们提高对算法的理解,但是可能对我们日常工作帮助也没特别大,比如在做图对比学习相关工作中,虽然对infonce为什么这样有疑问,但是还是拿来就用,也没啥毛病。
Question
- InfoNCE 估计器到底怎么推出来的??
- InfoNCE 中的温度会影响互信息下界的紧致程度吗?如果会的话怎么影响?
Reference
- DIM 知乎:https://zhuanlan.zhihu.com/p/277660074
- MINE 知乎:https://zhuanlan.zhihu.com/p/113455332
- MINE 论文:https://arxiv.org/pdf/1801.04062.pdf
- f-GAN 科学空间:https://kexue.fm/archives/6016
- 从 NCE 到 infoNCE 知乎:https://zhuanlan.zhihu.com/p/334772391
- 局部变分法,PRML:https://mqshen.gitbooks.io/prml/content/Chapter10/local_variational_method.html