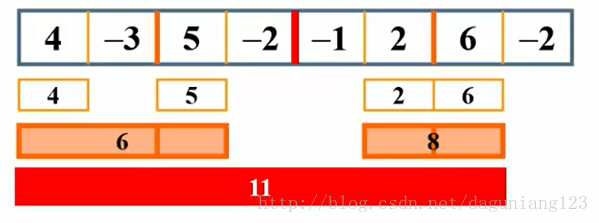
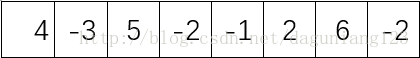题目：给你一组数，求它的子序列（连续的）最大和是多少（要是结果小于一输出0）；

如

4  -3  5  -2  -1  2  6  -2；

则是 4 -3 5 -2 -1 2 6 之和最大为11；

 本题采用分治的思想，就是先把这8个数对半分；

 然后在分 

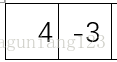
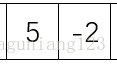
 最后

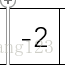
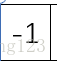
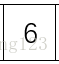
 我们把这一组数分到一个一个为止目的是求出每次分好之后这个序列的最大子序列和

这样的方便之处在于，假如你用暴力解决的话，你需要求出每种情况（也就是第1个数到第1，2，3.... ；第2个数到第2，3，4....），

然后比较，但是我们分完之后在合并的时候就无需考虑前面是否有情况会忽略，因为在此之前前面那一整个的最大子序列和已经求过了

 比如在合并4 -3 和5 -2 这一组的时候，你只需分别求出二组从中间向二边推的过程中的最大和值就行了，也就是左边先加-3，

 然后接着加4，最大和值就是1；右边先加 5 再加-2 最大和值就是5，因为加了-2反而小了，然后4 -3 5 -2 一整个的就是1+5=6；

同理

代码：

#include<stdio.h>
#define max(x,y) x>y?x:y
void f(int l,int r);
void mix(int l,int r);
int n;
int sum=0;
int a[100];
void f(int l,int r)
{

    if(l<r)
    {
        f(l,(l+r)/2);
        f((l+r)/2+1,r);
    }

    mix(l,r);
}

void mix(int l,int r)
{
    int mid=(l+r)/2;
    int maxl=0,suml=0;
    int maxr=0,sumr=0;
    for(int i=mid;i>=l;i--)
    {

        suml=suml+a[i];
        if(maxl<suml)
            maxl=suml;
    }

    for(int i=mid+1;i<=r;i++)
    {

        sumr=sumr+a[i];
        if(maxr<sumr)
            maxr=sumr;
    }

    if(sum<maxl+maxr)
        sum=maxl+maxr;


}


int main()
{

    scanf("%d",&n);
    for(int i=1;i<=n;i++)
    {
        scanf("%d",&a[i]);
    }
    f(1,n);
    printf("%d\n",sum);

    return 0;
}