算法力扣刷题记录六十【669. 修剪二叉搜索树】

前言

二叉搜索树操作。继续。
记录六十【669. 修剪二叉搜索树】

一、题目阅读

给你二叉搜索树的根节点 root ，同时给定最小边界low 和最大边界 high。通过修剪二叉搜索树，使得所有节点的值在[low, high]中。修剪树 不应该 改变保留在树中的元素的相对结构 (即，如果没有被移除，原有的父代子代关系都应当保留)。可以证明，存在唯一的答案。

所以结果应当返回修剪好的二叉搜索树的新的根节点。注意，根节点可能会根据给定的边界发生改变。

示例 1：
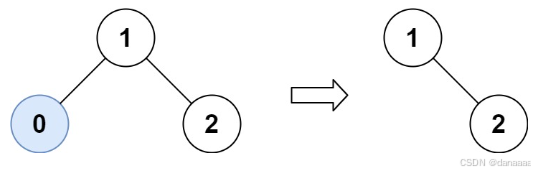
在这里插入图片描述

输入：root = [1,0,2], low = 1, high = 2
输出：[1,null,2]

示例 2：
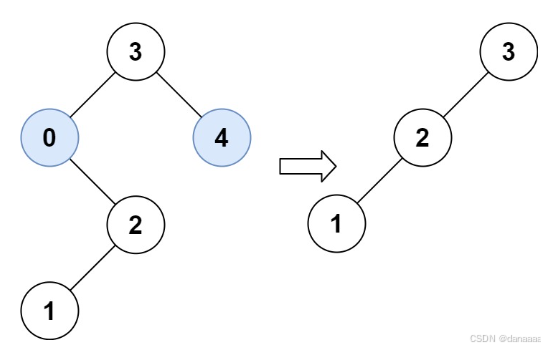
在这里插入图片描述

输入：root = [3,0,4,null,2,null,null,1], low = 1, high = 3
输出：[3,2,null,1]

提示：

树中节点数在范围 [1, 10^4] 内
0 <= Node.val <= 10^4
树中每个节点的值都是 唯一 的
题目数据保证输入是一棵有效的二叉搜索树
0 <= low <= high <= 10^4

二、尝试解答

理解题目

第一步：明白题目要求。把二叉搜索树中不在[low,right]之内的节点删除，但是不改变保留下来的节点原有的父子关系。这一定会修改二叉搜索树的结构。
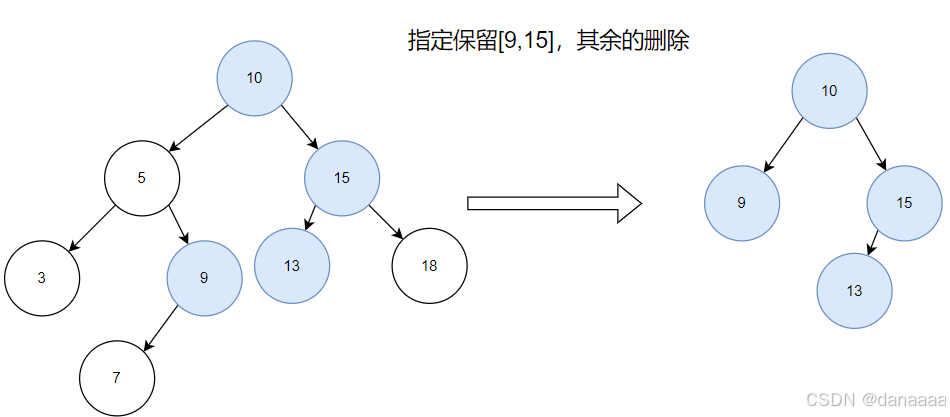
第二步：除了示例，画一个别的图，再研究一下过程。
在这里插入图片描述

思路

二叉搜索树：根据经验，先想根据节点的大小，能不能指明方向，只去一个方向呢？这种不遍历整个树，只是树中的一条路。pass，不行，因为上图显示，如果不遍历完整的树，无法保证所有边界外的节点都被删除。所以一定要遍历整个树。
遍历整个树，在二叉搜索树中：中序遍历得到有序递增的序列，判断边界进行剪枝，可以吗？分析：

先对左子树遍历，进行剪枝；返回剪枝之后的左子树。
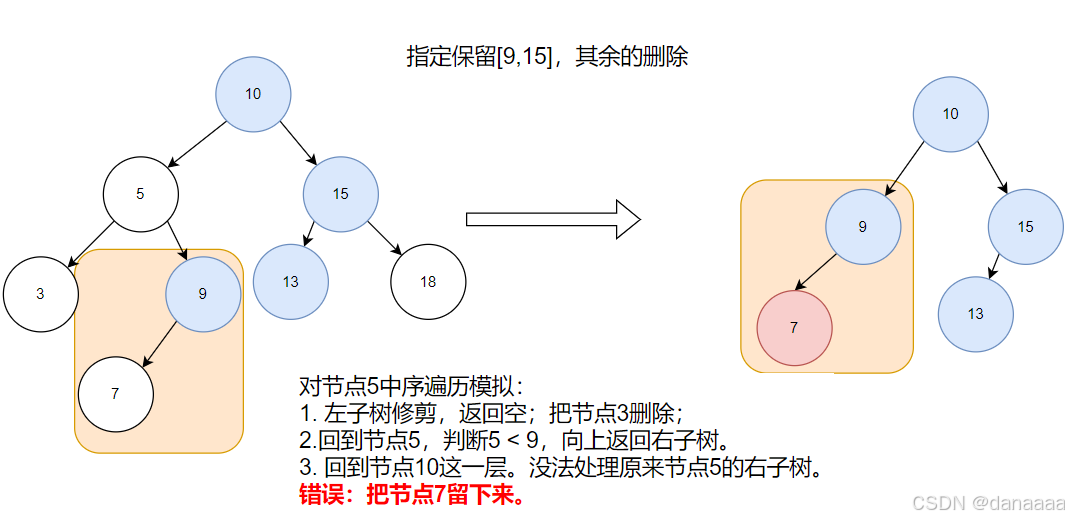
再对中间节点处理：如果中间节点 < 左边界，应该删除自己和左子树，返回右子树。可是这里返回上一层，右子树中存在 < 左边界的值怎么办，如下图？回到上一层就没办法再处理这一层的右子树。所以，中序遍历的逻辑不太正确。

所以应该后序遍历：先对左子树修剪；再对右子树修剪。回到中间判断向上一层返回哪边子树。接下来递归函数步骤完成：
递归参数：借助给定的主函数。参数：TreeNode* ，low和high。
递归返回值：返回修剪后的子树：TreeNode* 。
递归终止条件：root当前节点为空，说明到叶子节点return nullptr。
递归逻辑：

先修剪左子树，用root->left接住返回值；
再修剪右子树，用root->right接住返回值；
判断中间节点：如果小于low，返回右子树。如果大于high，返回左子树。剩余情况，返回root，自身修剪好的树。

代码实现【递归+后序遍历】

class Solution {
public:
    TreeNode* trimBST(TreeNode* root, int low, int high) {
        if(!root) return nullptr;
        //先对左子树剪枝
        root->left  = trimBST(root->left,low,high);
        //再对右子树剪枝
        root->right = trimBST(root->right,low,high);
        //在进行中间处理
        if(root->val < low){//在左边界之外
            return root->right;//返回右子树
        }else if(root->val > high){//在右边界之外
            return root->left;//返回左子树
        }else return root;//在界限之内，返回自身。
    }
};

三、参考学习

参考学习链接

学习内容

记录五十九【450.删除二叉搜索树中的节点】是删除一个指定的目标。也是删除节点：通过返回值向上一层返回，上一层用left或者right接住返回值，完成删除操作。
对比参考思路：

二、中思路，把一个树的左右子树都修剪完之后，再判断该节点是否符合条件，向上一层返回对应的子树；
参考思路：先判断中间节点和区间的关系，指明去哪个方向修剪：
- 如果root->val > high ，修剪右子树，可能右子树中存在符合区间的值，向上一层返回修剪的右子树。其实左子树不用做多余的操作；
- 如果root->val < high ，修剪左子树，可能左子树中存在符合区间的值，向上一层返回修剪的左子树。其实右子树不用做多余的操作；
- 如果root->val符合区间，修剪左子树和右子树。
- 总结：减少了一些节点操作，有针对性的修剪。

代码实现【递归+指明方向】：

class Solution {
public:
    TreeNode* trimBST(TreeNode* root, int low, int high) {
        if(!root) return nullptr;
        //判断中间节点，再针对修改
        if(root->val > high){
            TreeNode* left = trimBST(root->left,low,high);
            return left;
        }else if(root->val < low){
            TreeNode* right = trimBST(root->right,low,high);
            return right;
        }
        //自然如果该节点符合区间，那么去修剪左右子树。
        root->left = trimBST(root->left,low,high);
        root->right = trimBST(root->right,low,high);
        return root;
    }
};

迭代法：思路有些区别：

先把root根节点移到区间内；
先对左子树修剪，再对右子树修剪。

一般递归：需要一个栈或者队列来放节点。这里不需要因为二叉搜索树会指明方向。

参考代码【迭代法】：

class Solution {
public:
    TreeNode* trimBST(TreeNode* root, int low, int high) {
        if(!root) return nullptr;//如果根节点是空。说明给的整个树是空。

        //把root先调整到[low,high]之间
        while(root && (root->val < low || root->val > high)){
            if(root->val < low ) root = root->right;
            else root = root->left;
        }
        //先修剪左子树
        TreeNode* cur = root;
        while(cur){
            //下面必须是while，不能是if。把当前cur->left循环剪到区间内，再开始进一步子树的修剪。
            while(cur->left && cur->left->val < low ){//root已经在区间，左子树 < root，所以只可能小于low
                cur->left = cur->left->right;
            }
            cur = cur->left;
        }

        cur=root;//把cur回到root。
        //重新开始右子树修剪
        while(cur){
            while(cur->right && cur->right->val > high){//对照左子树。右子树只可能>high
                cur->right = cur->right->left;
            }
            cur = cur->right;
        }
        return root;
    }
};

总结

【669. 修剪二叉搜索树】
在这里插入图片描述
（欢迎指正，转载标明出处）

算法力扣刷题记录 六十【669. 修剪二叉搜索树】

前言