算法力扣刷题记录九十【739. 每日温度】

前言

单调栈第一篇。单调栈解题思路如何？

一、题目阅读

给定一个整数数组 temperatures ，表示每天的温度，返回一个数组 answer ，其中 answer[i] 是指对于第 i 天，下一个更高温度出现在几天后。如果气温在这之后都不会升高，请在该位置用 0 来代替。

示例 1:

输入: temperatures = [73,74,75,71,69,72,76,73]
输出: [1,1,4,2,1,1,0,0]

示例 2:

输入: temperatures = [30,40,50,60]
输出: [1,1,1,0]

示例 3:

输入: temperatures = [30,60,90]
输出: [1,1,0]

提示：

1 <= temperatures.length <= 10^5
30 <= temperatures[i] <= 100

二、思路

【739. 每日温度】参考学习链接

暴力两层for循环。第一层固定起始下标，内层for循环找第一个比它大的数值的下标，做减法。

class Solution {
public:
    vector<int> dailyTemperatures(vector<int>& temperatures) {
        vector<int> result(temperatures.size(),0);//初始化0
        for(int i = 0;i <temperatures.size();i++){
            for(int j = i+1;j < temperatures.size();j++){
                if(temperatures[j] <= temperatures [i]) continue;
                result[i] = j-i;
                break;//找到第一个大的数值，就可以break本层循环
            }
        }
        return result;
    }
};

时间复杂度是O(n²)，提交后超出时间限制。存在用例无法通过。

一维数组，寻找任一个元素的右边或者左边第一个比自己大或者小的元素的位置，就要想到用单调栈。 时间复杂度为O(n)。
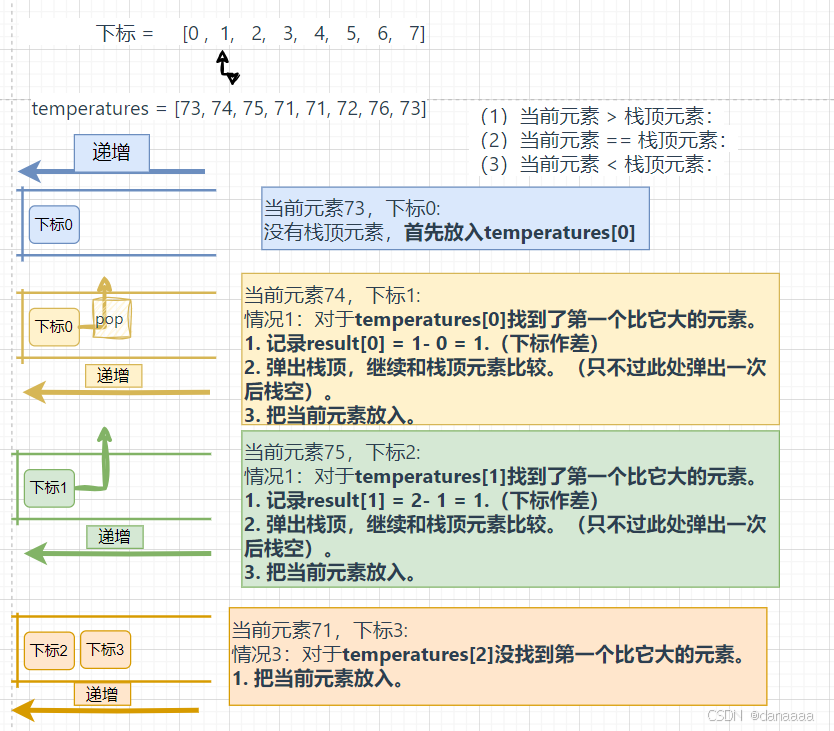
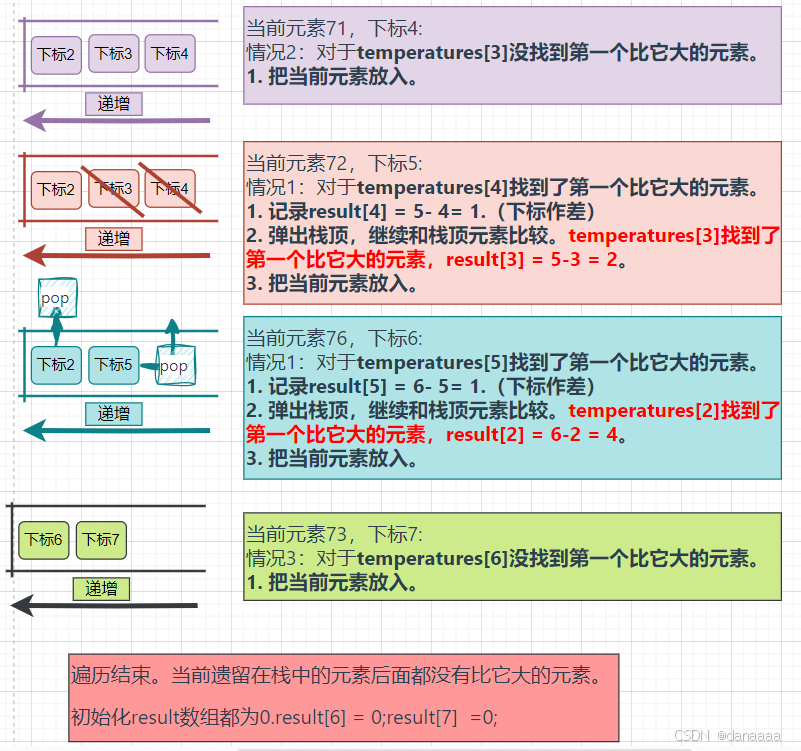
本题求：该元素右边第一个比它大的元素的位置，获得距离。所以用单调栈解决。那么这个栈维护的是什么元素? 栈中始终保持递增或者递减。

栈中放元素所在的下标。获得元素就通过数组temperature[i]。
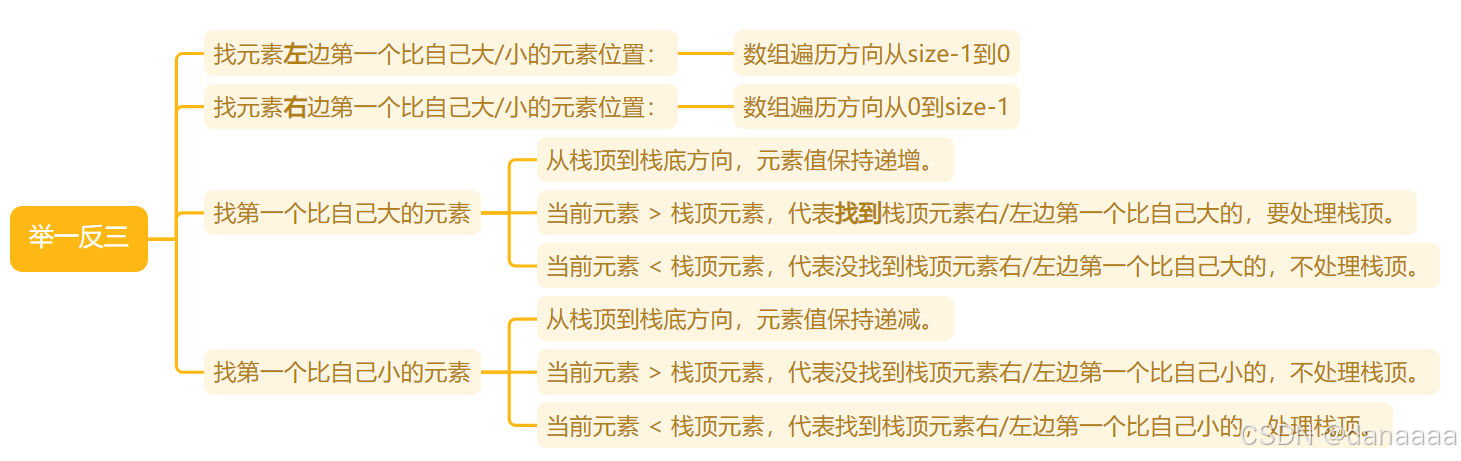
结论：从栈口到栈底 递增——求当前元素的右边/左边第一个比自己大的元素（的位置）；递减——求当前元素的右边/左边第一个比自己小的元素（的位置）；
原数组遍历顺序结论：
- 如果求当前元素的右边第一个比自己大/小的元素，那么从0到size-1；因为栈里放已经遍历过的元素，当前的元素在已经遍历过的元素的右边；
- 如果求当前元素的左边第一个比自己大/小的元素，那么从size-1到0；因为栈里放已经遍历过的元素，当前的元素在已经遍历过的元素的左边；
栈的作用：记录已经遍历过哪些元素。和当前遍历的元素比较，才知道当前的元素有没有比之前的元素大/小。

过程：记录结果的数组（即返回值），每一个结果的顺序不是依次确定的，可能跳跃性的确定。
总结：

单调栈中放下标
当前元素 > 栈顶元素：记录结果、pop元素、循环判断直至栈顶元素不大于当前元素、并放入当前元素；
当前元素 == 栈顶元素：直接放入。
当前元素 < 栈顶元素：直接放入。

三、代码实现【单调栈】

3.1 根据思路个人实现

时间复杂度O(N).

class Solution {
public:
    vector<int> dailyTemperatures(vector<int>& temperatures) {
        vector<int> result(temperatures.size(),0);//初始化0
        stack<int> st;
        if(!temperatures.empty()) st.push(0);//先放入下标0
        for(int i = 1;i < temperatures.size();i++){
            while(!st.empty() && temperatures[i] > temperatures[st.top()]){//当前元素temperature[i]大于栈顶元素
                result[st.top()] = i - st.top();
                st.pop();
            }
            st.push(i);//直接放入,要么栈已经空或者当前元素小于等于栈顶元素
        }
        return result;
    }
};

参考代码：第一个版本如下，上面是精简版本。

// 版本一
class Solution {
public:
    vector<int> dailyTemperatures(vector<int>& T) {
        // 递增栈
        stack<int> st;
        vector<int> result(T.size(), 0);
        st.push(0);
        for (int i = 1; i < T.size(); i++) {
            if (T[i] < T[st.top()]) {                       // 情况一
                st.push(i);
            } else if (T[i] == T[st.top()]) {               // 情况二
                st.push(i);
            } else {
                while (!st.empty() && T[i] > T[st.top()]) { // 情况三
                    result[st.top()] = i - st.top();
                    st.pop();
                }
                st.push(i);
            }
        }
        return result;
    }
};

四、举一反三

总结

在这里插入图片描述
（欢迎指正，转载标明出处）

算法力扣刷题记录 九十【739. 每日温度】

前言