目录:
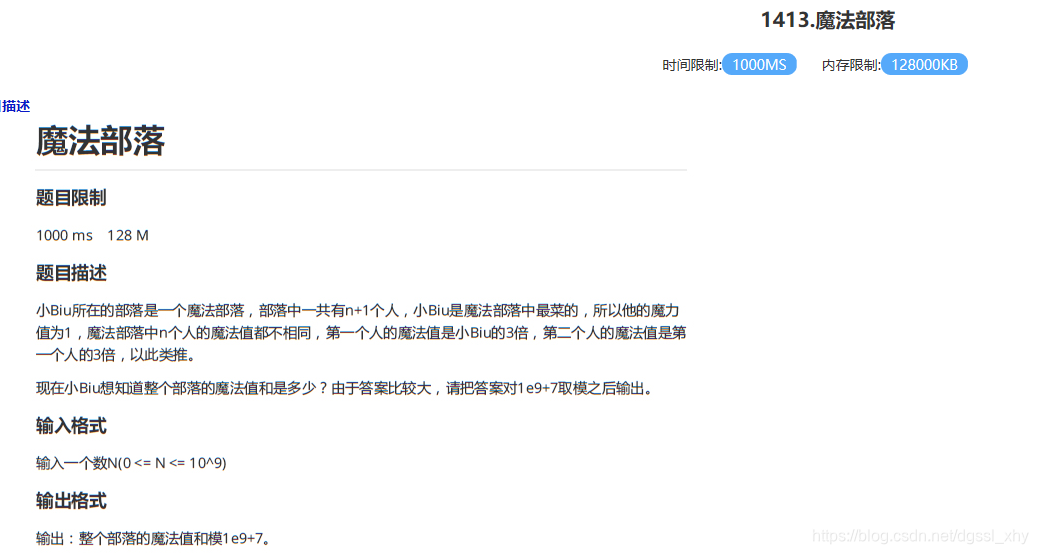
T1:魔法部落
T2:圆盘
T3:棋盘行走
T4:走方格
一套整体不难但需要细节的题
T1:
分析:
可以看出 这是个公比为
3
3
3的等比序列
q
q
q为公比
众所周知 等比数列前
n
n
n项之和为:
q
(
n
+
1
)
/
(
q
−
1
)
q^{(n+1)}/(q-1)
q(n+1)/(q−1)
也就是:
3
(
n
+
1
)
/
2
3^{(n+1)}/2
3(n+1)/2
所以这样再快速幂
+
m
o
d
+mod
+mod可喜提
60
p
t
s
60pts
60pts 而且会
w
a
wa
wa一些点
为什么呢?
因为
x
/
y
x/y
x/y再
m
o
d
mod
mod 可能会出现负数 所以要逆元求解
最后可得:
q
(
n
+
1
)
/
(
q
−
1
)
q^{(n+1)}/(q-1)
q(n+1)/(q−1)
m
o
d
(
1
e
9
+
7
)
mod(1e9+7)
mod(1e9+7)
=
q
(
n
+
1
)
×
(
1
e
9
+
7
+
1
)
/
2
=q^{(n+1)}\times(1e9+7+1)/2
=q(n+1)×(1e9+7+1)/2
m
o
d
(
1
e
9
+
7
)
mod (1e9+7)
mod(1e9+7)
=
q
(
n
+
1
)
×
5
e
8
+
4
=q^{(n+1)}\times5e8+4
=q(n+1)×5e8+4
m
o
d
(
1
e
9
+
7
)
mod(1e9+7)
mod(1e9+7)
CODE:
#include<iostream>
#include<cstdio>
#include<algorithm>
using namespace std;
typedef long long ll;
const long long p=1e9+7;
const long long s=5e8+4;
ll n,ans,qwq=1;
void ksm(ll n)
{
long long tmp=3;
while(n){
if(n&1){
qwq=(qwq*tmp)%p;
}
tmp=(tmp*tmp)%p;
n>>=1;
}
}
int main(){
scanf("%lld",&n);
ksm(n+1);
ans=(qwq-1)*s%p;
printf("%lld",ans);
return 0;
}