哈希表的定义

哈希存储的基本思想是以关键字Key为自变量，通过一定的函数关系（散列函数或哈希函数），计算出对应的函数值（哈希地址），以这个值作为数据元素的地址，并将数据元素存入到相应地址的存储单元中。

查找时再根据要查找的关键字采用同样的函数计算出哈希地址，然后直接到相应的存储单元中去取要找的数据元素即可。

哈希表的应用

哈希表(hash table)是实现字典操作的一种有效的数据结构。

尽管最坏的情况下，散列表中查找一个元素的时间与链表中查找的时间相同，达到了O(n)。然而实际应用中，散列的查找的性能是极好的。在一些合理的假设下，在散列表中查找一个元素的平均时间是O(1)。

建立哈希表操作步骤

1) step1 取数据元素的关键字key，计算其哈希函数值（地址）。若该地址对应的存储空间还没有被占用，则将该元素存入；否则执行step2解决冲突。

2) step2 根据选择的冲突处理方法，计算关键字key的下一个存储地址。若下一个存储地址仍被占用，则继续执行step2，直到找到能用的存储地址为止。

常用的哈希函数

构造哈希函数的方法有很多，总的原则是尽可能将关键字集合空间均匀的映射到地址集合空间中，同时尽可能降低冲突发生的概率。

1、除留余数法：

H(Key) = key % p  (p ≤ m)

取关键字除以p的余数作为哈希地址，p最好选择一个小于或等于m（哈希地址集合的个数）的某个最大素数

2、直接地址法

H(Key) = a * Key + b；这个“a，b”是常量。

3、数字分析法

比如有一组key1=112233，key2=112633，key3=119033，

针对这样的数我们分析数中间两个数比较波动，其他数不变。那么我们取key的值就可以是 key1=22,key2=26,key3=90。

4、平方取中法

此处忽略，见名识意。

5、折叠法

比如key=135790，要求key是2位数的散列值。那么我们将key变为13+57+90=160，然后去掉高位“1”,此时key=60，

以上五种哈希关系的目的就是地址与每一位的key都相关，来做到“散列地址”尽可能分散。

冲突处理方法

我们知道影响哈希查找效率的一个重要因素是哈希函数本身。当两个不同的数据元素的哈希值相同时，就会发生冲突。为减少发生冲突的可能性，哈希函数应该将数据尽可能分散地映射到哈希表的每一个表项中。

解决冲突的方法有以下两种：

(1) 开放地址法

如果两个数据元素的哈希值相同，则在哈希表中为后插入的数据元素另外选择一个表项。

当程序查找哈希表时，如果没有在第一个对应的哈希表项中找到符合查找要求的数据元素，程序就会继续往后查找，直到找到一个符合查找要求的数据元素，或者遇到一个空的表项。

①.线性探测法

这种方法在解决冲突时，依次探测下一个地址，直到有空的地址后插入，若整个空间都找遍仍然找不到空余的地址，产生溢出。

Hi =( H(Key) + di ) % m  ( i = 1,2,3,...,k , k ≤ m-1 )

地址增量 di = 1,2,...,m-1 , 其中 i 为探测次数

②.二次探测法

地址增量序列为：di = 1^2，-1^2，2^2，-2^2 ，...，q^2，-q^2  （q ≤ m/2）

③.双哈希函数探测法

Hi =( H(Key) + i * RH(Key) ) % m      ( i = 1,2,3,..., m-1 )

H(Key) , RH(Key) 是两个哈希函数，m为哈希表长度。

先用第一个哈希函数对关键字计算哈希地址，一旦产生地址冲突，再用第二个函数确定移动的步长因子，最后通过步长因子序列由探测函数寻找空余的哈希地址。

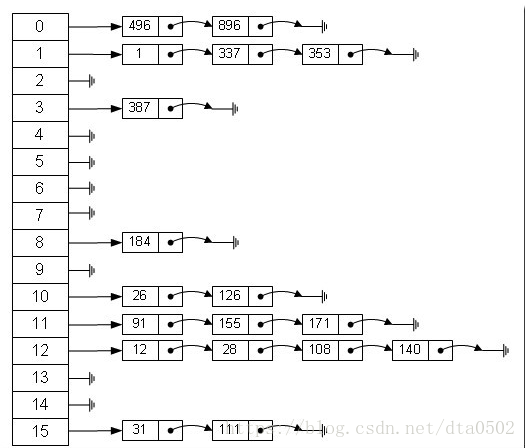
H1 = ( a+b )%m , H2 = ( a + 2b )%m , ... , Hm-1 = ( a+(m-1)*b )%m

(2) 链地址法

将哈希值相同的数据元素存放在一个链表中，在查找哈希表的过程中，当查找到这个链表时，必须采用线性查找方法。

Python字典dict的实现是使用开放寻址法中的二次探查来解决冲突的。

转载于：https://www.cnblogs.com/5poi/p/7273743.html

参考链接：https://stackoverflow.com/questions/327311/how-are-pythons-built-in-dictionaries-implemented