目录
一 人工智能、机器学习和深度学习的区别
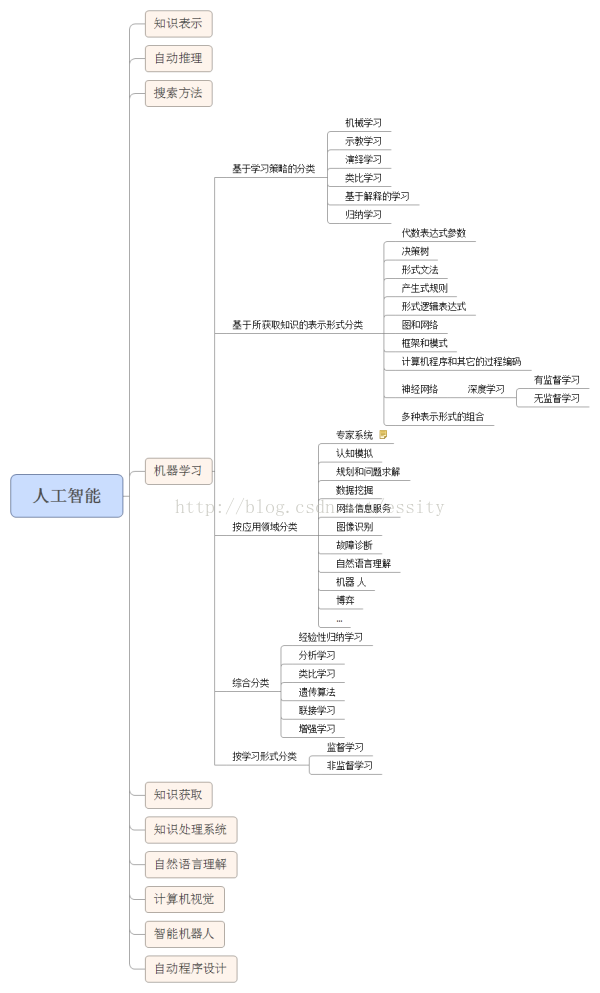
从1956年夏季首次提出“人工智能”这一术语开始,科学家们尝试了各种方法来实现它。这些方法包括SVM、决策树、K近邻、K-Means、回归算法、专家系统、归纳逻辑、聚类等等,但这些都是假智能。直到人工神经网络技术的出现,才让机器拥有了“真智能”。训练深度神经网络的过程就叫做深度学习。
机器学习,实现人工智能的方法之一;深度学习,实现机器学习的技术之一。尤其是2015年以来,人工智能开始大爆发。人工智能的学习能力分为两大部分,知识的学习和思维逻辑的学习重组。前者起点甚低,适应性训练都可以看作是学习;后者起点甚高,至今只可遥望和意味。
二 机器学习
机器学习是一种概念:不需要写任何与问题有关的特定代码,泛型算法(Generic Algorithms)就能告诉你一些关于你数据的有趣结论。不用编码,你将数据输入泛型算法当中,它就会在数据的基础上建立出它自己的逻辑。机器学习方法是计算机利用已有的数据(经验),得出了某种模型(迟到的规律),并利用此模型预测未来(是否迟到)的一种方法。
What is Machine Learning?
Two definitions of Machine Learning are offered. Arthur Samuel described it as: “the field of study that gives computers the ability to learn without being explicitly programmed.” This is an older, informal definition.
Tom Mitchell provides a more modern definition: “A computer program is said to learn from experience E with respect to some class of tasks T and performance measure P, if its performance at tasks in T, as measured by P, improves with experience E.”
Example: playing checkers.
E = the experience of playing many games of checkers
T = the task of playing checkers.
P = the probability that the program will win the next game.
In general, any machine learning problem can be assigned to one of two broad classifications:
Supervised learning and Unsupervised learning.
-----吴恩达《Machine Learning》
三 深度学习
“深度学习”已成为用于描述使用多层神经网络的过程的标准术语, 多层神经网络是一类极为灵活的可利用种类繁多的数学方法以及不同数学方法组合的模型。深度学习的强大之处在于当决定如何最有效地利用数据时, 它能够赋予模型更大的灵活性。 人们无需盲目猜测应当选择何种输入。 一个调校好的深度学习模型可以接收所有的参数, 并自动确定输入值的有用高阶组合。
四 准备
- 目前用计算机处理得较多的数学计算主要分为以下两类:
第一类是数值计算,它以数值数组作为运算对象,给出数值解;计算过程中可能会产生误差累积问题,影响了计算结果的精确性;计算速度快,占用资源少。
第二类是符号计算,它以符号对象和符号表达式作为运算对象,给出解析解;运算不受计算误差累积问题的影响;计算指令简单;占用资源多,计算耗时长。
- 数值计算方法成为了科学计算的重要手段, 它研究怎样利用计算丁.具来求出数学问题的数值解。 数值计算方法的计算对象是微积分 、 线性代数 、 插值与逼近及最小二乘拟合 、 数值积分与数值微分、 矩阵的特征值与特征向量求解 、 线性方程组与非线性方程求根, 以及微分方程数值解法等数学问题, 这些是模式识别 、 数据分析及自动制造等机器学习领域需要应用的数学。
- 符号计算是专家系统等机器学习领域需要应用的数学, 在符号计算中, 计算机处理的数据和得到的结果都是符号。 符号既可以是字母和公式, 也可以是数值, 其运算以推理解析的方式进行, 不受计算误差积累问题闲扰, 汁算结果为完全正确的封闭解或任意精度的数值解, 这意味着符号计算给出的结果能避免因舍人误差而引起的问题。
- 现代科学研究的方法主要有三种:理论论证、科学实验、科学计算。计算机进行科学计算,都必须建立相应的数学模型,并研究其适合于计算机编程的计算方法。科学计算平台已经成为科学研究必要的基础条件平台,有力地推动了科学研究的发展和工程技术的进步。
五 卷积
六 傅里叶变换
七 模型推理部署——基础概念篇
本节内容来自这里。
1 训练(training)vs推理(inference)
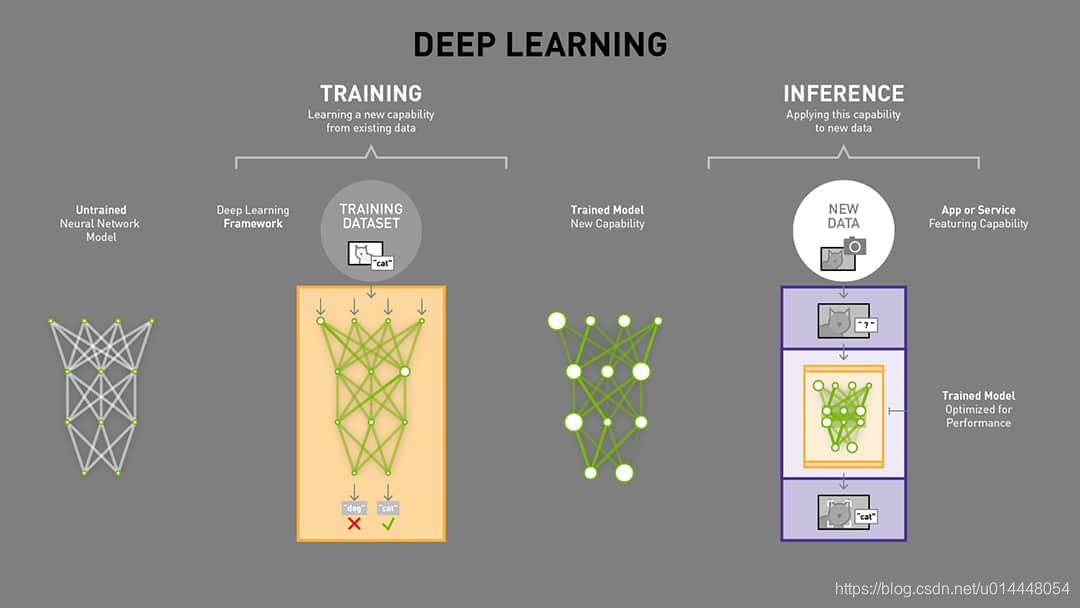
训练是通过从已有的数据中学习到某种能力,而推理是简化并使用该能力,使其能快速、高效地对未知的数据进行操作,以获得预期的结果。
训练是计算密集型操作,模型一般都需要使用大量的数据来进行训练,通过反向传播来不断的优化模型的参数,以使得模型获取某种能力。在训练的过程中,我们常常是将模型在数据集上面的拟合情况放在首要位置的。而推理过程在很多场景下,除了模型的精度外,还更加关注模型的大小和速度等指标。这就需要对训练的模型进行一些压缩、剪枝或者是操作上面的计算优化。
我们做算法的最终目的都是希望自己的方法可以真正的应用起来,那么在对模型部署上面,每一个算法工程师都应该有一些基本的sense。下面本文会简单介绍一些推理时比较关注的指标。
2 重要指标
2.1 Throughput 吞吐量
单位时间内所处理的数据量 一般用 推理/秒 或者 样本/秒 衡量。每台服务器的吞吐量对于数据中心能否合算的扩展至关重要。
# 包含并行情况
def calc_ips(batch_size, time):
# 全局进程个数
world_size = (
torch.distributed.get_world_size() if torch.distributed.is_initialized() else 1
)
tbs = world_size * batch_size
return tbs / time
2.2 Latency 延迟
执行一次推理所花的时间,单位一般为ms。低延迟对于实时且快速增长地推理服务至关重要。一般在压测时,我们都是通过增加并发数,来观察 Latency 平均线、90线、 95线和99线
# time_list 为每个请求从发送到返回的时间列表
avg = np.mean(time_list)
cf_90 = max(time_list[:int(len(time_list) * 0.90)])
cf_95 = max(time_list[:int(len(time_list) * 0.95)])
cf_99 = max(time_list[:int(len(time_list) * 0.99)])
或者直接使用numpy提供的方法来求
# 根据不同的线来改变q
np.quantile(time_list, q, interpolation=“nearest”)
2.3 Accuracy 准确率
训练后的模型能够提供正确结果的能力。一般推理时,我们会评估模型在模型压缩或者优化后能够和训练时达到一样或者可接受的相似效果。模型是否正确部署,结果具有幂等性。同时根据应用场景的情况,我们可以针对自己在意的指标进行衡量(和训练时相同)。例如:一般针对图像分类而言,我们会参考top-1 or top-5的准确率。
2.4 Memory usage 内存使用情况
在众多场景下,在推理过程中很关注内存的使用情况。尤其是在多个网络模型并且内存资源有限的系统中尤为重要。另外,有时也需要在意内存的利用率情况,这对于评估资源是否浪费以及模型外工程方面的优化方向至关重要。在GPU设备上,我们可以使用下面命令来监控内存的使用情况。
nvidia-smi
watch -n 1 nvidia-smi #每个1s更新显示
2.5 Efficiency 效率
单位功率的吞吐量, 一般单位为 performance/watt。Efficiency是数据中心扩展合算分析的另一个关键因素。因为服务器、服务器机架和整个数据中心必须在固定的功率预算内运行。
3 FLOPs
是floating point operations的缩写(s表复数),意指浮点运算数,理解为计算量。可以用来衡量算法/模型的复杂度。
4 FLOPS
是floating point operations per second的缩写,意指每秒浮点运算次数,理解为计算速度。是一个衡量硬件性能的指标。
5 硬件相关
在大数据的时代,对于各种卡的选择我们也是需要有一点点了解的,很多优化操作都是针对不同的卡进行的。我现在用到比较多的就是 V100和T4,两者相关信息对比:
更多详见:List of Nvidia graphics processing units
6 参考文献
https://en.wikipedia.org/wiki/List_of_Nvidia_graphics_processing_units
https://blogs.nvidia.com/blog/2016/08/22/difference-deep-learning-training-inference-ai/
https://docs.nvidia.com/deeplearning/tensorrt/developer-guide/index.html#overview
八 平方差(difference of two squares)
平方差公式,是数学公式的一种,它属于乘法公式、因式分解及恒等式,被普遍使用。平方差指一个平方数或正方形,减去另一个平方数或正方形得来的乘法公式:
a
2
−
b
2
=
(
a
+
b
)
(
a
−
b
)
a^2-b^2 = (a+b)(a-b)
a2−b2=(a+b)(a−b)
九 方差(variance/deviation Var)
方差(variance)是衡量随机变量或一组数据时离散程度的度量。概率论中方差用来度量随机变量和其数学期望(即均值)之间的偏离程度。统计中的方差(样本方差)是每个样本值与全体样本值的平均数之差的平方值的平均数。
概率论中的方差表示方法 :
样本方差,无偏估计、无偏方差(unbiased variance)。对于一组随机变量,从中随机抽取N个样本,这组样本的方差就 是Xi^2平方和除以N-1。这可以推导出来的。
S
2
=
1
n
−
1
∑
i
=
1
n
(
X
i
−
X
‾
)
2
S^2=\frac{1}{n-1} \sum_{i=1}^{n}(X_i-\overline{X})^2
S2=n−11i=1∑n(Xi−X)2
总体方差,也叫做有偏估计,其实就是我们从初高中就学到的那个标准定义的方差,除数是N。
S
2
=
1
n
∑
i
=
1
n
(
X
i
−
X
‾
)
2
S^2=\frac{1}{n} \sum_{i=1}^{n}(X_i-\overline{X})^2
S2=n1i=1∑n(Xi−X)2
X
‾
\overline{X}
X表示集合D的数学期望(即均值):
E
(
D
)
=
X
‾
=
1
n
∑
i
=
1
n
x
i
E(D)=\overline{X}=\frac{1}{n}\sum_{i=1}^nx_i
E(D)=X=n1∑i=1nxi
统计中的方差表示方法 :
σ
2
=
∑
(
X
−
μ
)
2
N
\sigma^2=\frac{\sum(X-\mu)^2}{N}
σ2=N∑(X−μ)2
σ
2
\sigma^2
σ2为总体方差,
X
X
X为变量,
μ
\mu
μ为总体均值,
N
N
N为总体均例数,这里的
μ
\mu
μ有时也用
X
‾
\overline{X}
X表示,也就是所有样本的均值。
十 标准差(Standard Deviation)
又常称均方差或者标准偏差,是方差的算术平方根,用
σ
\sigma
σ表示。标准差能反映一个数据集的离散程度。其实方差与标准差都是反映一个数据集的离散程度,只是由于方差出现了平方项造成量纲的倍数变化,无法直观反映出偏离程度,于是出现了标准差。公式为:
σ
=
1
N
∑
i
=
1
N
(
x
i
−
μ
)
2
\sigma=\sqrt{\frac{1}{N}\sum_{i=1}^N(x_i-\mu)^2}
σ=N1i=1∑N(xi−μ)2
同样也存在与方差一样的情况:如是总体(即估算总体方差),根号内除以
N
N
N;如是抽样(即估算样本方差),根号内除以
(
N
−
1
)
(N-1)
(N−1)。
十一 均方误差(MSE)
衡量“平均误差”的一种较方便的方法。是参数估计值与参数真值之差的平方的期望值(均值)。常运用在信号处理的滤波算法(最小均方差)中,表示此时观测值observed与估计值predicted之间的偏差,即:
M
S
E
=
1
N
∑
t
=
1
N
(
o
b
s
e
r
v
e
d
t
−
p
r
e
d
i
c
t
e
d
t
)
2
MSE=\frac{1}{N}\sum_{t=1}^N(observed_t-predicted_t)^2
MSE=N1t=1∑N(observedt−predictedt)2
十二 均方根值(RMS)
称方均根值或有效值,它的计算方法是先平方、再平均、然后开方。
X
r
m
s
=
∑
i
=
1
N
N
=
X
1
2
+
X
2
2
+
⋯
+
X
N
2
N
X_{rms}=\sqrt{\frac{\sum_{i=1}^N}{N}}=\sqrt{\frac{X_1^2+X_2^2+\cdots+X_N^2}{N}}
Xrms=N∑i=1N=NX12+X22+⋯+XN2
十三 均方根误差(Root Mean Squared Error,RMSE)
是均方误差的算术平方根。
R
M
S
E
=
1
N
∑
t
=
1
N
(
o
b
s
e
r
v
e
d
t
−
p
r
e
d
i
c
t
e
d
t
)
2
RMSE=\sqrt{\frac{1}{N}\sum_{t=1}^N(observed_t-predicted_t)^2}
RMSE=N1t=1∑N(observedt−predictedt)2
十四 梯度
1 梯度
梯度的本意是一个向量(矢量),表示某一函数在该点处的方向导数沿着该方向取得最大值,即函数在该点处沿着该方向(此梯度的方向)变化最快,变化率最大(为该梯度的模)在单变量的实值函数的情况,梯度只是导数,或者,对于一个线性函数,也就是线的斜率。(—百度百科)
一元函数
y
=
f
(
x
)
y=f(x)
y=f(x)在点
x
0
x_0
x0处的梯度是:
d
f
d
x
∣
x
=
x
0
\frac{d_f}{d_x}|_{x=x_0}
dxdf∣x=x0;
二元函数
z
=
f
(
x
,
y
)
z=f(x,y)
z=f(x,y)在点
(
x
0
,
y
0
)
(x_0,y_0)
(x0,y0)处的梯度是:
(
∂
f
∂
x
∣
(
x
0
,
y
0
)
,
∂
f
∂
y
∣
(
x
0
,
y
0
)
)
(\frac{\partial{f}}{\partial{x}}|_{(x_0,y_0)},\frac{\partial{f}}{\partial{y}}|_{(x_0,y_0)})
(∂x∂f∣(x0,y0),∂y∂f∣(x0,y0));
简而言之,对多元函数的的各个自变量求偏导数,并把求得的这些偏导数写成向量的形式,就是梯度。常把函数
f
f
f的梯度简记为:
∇
f
\nabla{f}
∇f或者
grad
f
\text{grad}f
gradf。
例子:
函数 φ = 2 x + 3 y 2 + s i n ( x ) \varphi=2x+3y^2+sin(x) φ=2x+3y2+sin(x)的梯度是:
∇ φ = ( ∂ φ ∂ x , ∂ φ ∂ y , ∂ φ ∂ z ) = ( 2 , 6 y , − c o s ( z ) ) \nabla\varphi=(\frac{\partial{\varphi}}{\partial{x}},\frac{\partial{\varphi}}{\partial{y}},\frac{\partial{\varphi}}{\partial{z}})=(2,6y,-cos(z)) ∇φ=(∂x∂φ,∂y∂φ,∂z∂φ)=(2,6y,−cos(z))
(注意:梯度是一个向量)
要明确梯度是一个向量,是一个n元函数
f
f
f 关于n个变量的偏导数,比如三元函数
f
f
f 的梯度为
(
f
x
,
f
y
,
f
z
)
(fx,fy,fz)
(fx,fy,fz) ,二元函数f的梯度为
(
f
x
,
f
y
)
(fx,fy)
(fx,fy) ,一元函数
f
f
f 的梯度为
f
x
fx
fx。然后要明白梯度的方向是函数
f
f
f 增长最快的方向,梯度的反方向是
f
f
f 降低最快的方向。
2 梯度下降的场景假设
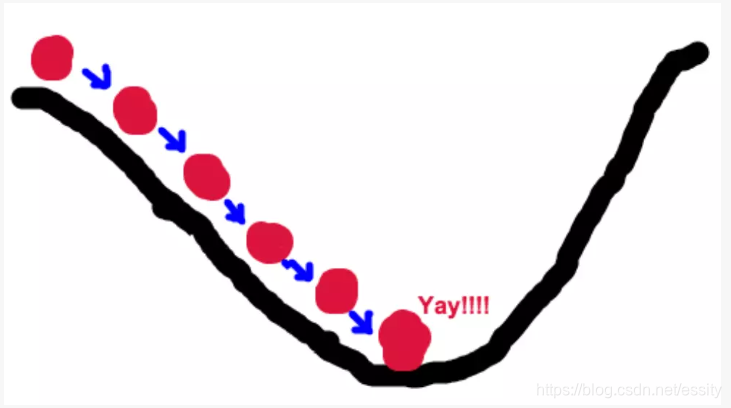
梯度下降法的基本思想可以类比为一个下山的过程。假设这样一个场景:一个人被困在山上,需要从山上下来(i.e. 找到山的最低点,也就是山谷)。但此时山上的浓雾很大,导致可视度很低。因此,下山的路径就无法确定,他必须利用自己周围的信息去找到下山的路径。这个时候,他就可以利用梯度下降算法来帮助自己下山。具体来说就是,以他当前的所处的位置为基准,寻找这个位置最陡峭的地方,然后朝着山的高度下降的地方走,同理,如果我们的目标是上山,也就是爬到山顶,那么此时应该是朝着最陡峭的方向往上走。然后每走一段距离,都反复采用同一个方法,最后就能成功的抵达山谷。
我们同时可以假设这座山最陡峭的地方是无法通过肉眼立马观察出来的,而是需要一个复杂的工具来测量,同时,这个人此时正好拥有测量出最陡峭方向的能力。所以,此人每走一段距离,都需要一段时间来测量所在位置最陡峭的方向,这是比较耗时的。那么为了在太阳下山之前到达山底,就要尽可能的减少测量方向的次数。这是一个两难的选择,如果测量的频繁,可以保证下山的方向是绝对正确的,但又非常耗时,如果测量的过少,又有偏离轨道的风险。所以需要找到一个合适的测量方向的频率,来确保下山的方向不错误,同时又不至于耗时太多!
引自:六尺帐篷 链接:https://www.jianshu.com/p/c7e642877b0e
3 代价函数(Cost Function)
注:文中使用的符号
:
=
:=
:= 是赋值运算符,它本身是计算机语言中的符号,屋恩达使用这个符号,所以网上很多资料也为了保持一致使用这个符号,但是在数学中,并没有见过这个符号!!!!!!
代价函数(有的地方也叫损失函数,Loss Function),因为训练模型的过程就是优化代价函数的过程,代价函数对每个参数的偏导数就是梯度下降中提到的梯度,防止过拟合时添加的正则化项也是加在代价函数后面的。
我们可以用成本函数来衡量假设函数的准确性。它取输入x后的假设值和实际输出y的所有结果的平均值差(实际上是平均值的更漂亮的版本)。
J
(
θ
0
,
θ
1
)
=
1
2
m
∑
i
=
1
m
(
y
^
i
−
y
i
)
2
=
1
2
m
∑
i
=
1
m
(
h
θ
(
x
i
)
−
y
i
)
2
J(\theta_0, \theta_1) = \dfrac {1}{2m} \displaystyle \sum _{i=1}^m \left ( \hat{y}_{i}- y_{i} \right)^2 = \dfrac {1}{2m} \displaystyle \sum _{i=1}^m \left (h_\theta (x_{i}) - y_{i} \right)^2
J(θ0,θ1)=2m1i=1∑m(y^i−yi)2=2m1i=1∑m(hθ(xi)−yi)2
说明一下这个式子的含义:
m
m
m 是数据集中点的个数;
1
/
2
1/2
1/2这样是为了在求梯度的时候,二次方乘下来就和这里的
½
½
½抵消了,自然就没有多余的常数系数,方便后续的计算,同时对结果不会有影响;
y
y
y 是数据集中每个点的真实值;
h
h
h 是预测值。
这个函数因此也称为 “Squared error function”,或者"Mean squared error"。
J
J
J 表示给定的函数预测值和实际值Y的均方差,它反映的是预测值与实际值的一个偏离的程度。
我们是否可以用梯度下降算法来快速的无限逼近
θ
\theta
θ,使得
J
J
J 达到最小,当
J
J
J 达到最小的时候,那么我们这个时候的
θ
\theta
θ,不就是无限接近真实且理想的的那个权重
θ
\theta
θ 么?
4 梯度下降实例分析
梯度下降的基本过程就和下山的场景很类似。
首先,我们有一个可微分的函数。这个函数就代表着一座山。我们的目标就是找到这个函数的最小值,也就是山底。根据之前的场景假设,最快的下山的方式就是找到当前位置最陡峭的方向,然后沿着此方向向下走,对应到函数中,就是找到给定点的梯度 ,然后朝着梯度相反的方向,就能让函数值下降的最快!因为梯度的方向就是函数之变化最快的方向。所以,我们重复利用这个方法,反复求取梯度,最后就能到达局部的最小值,这就类似于我们下山的过程。而求取梯度就确定了最陡峭的方向,也就是场景中测量方向的手段。那么为什么梯度的方向就是最陡峭的方向呢?
通过实例说明:
对于Rosenbrock函数:
f
(
x
,
y
)
=
(
1
−
x
)
2
+
100
(
y
−
x
2
)
2
f(x,y)=(1-x)^2+100(y-x^2)^2
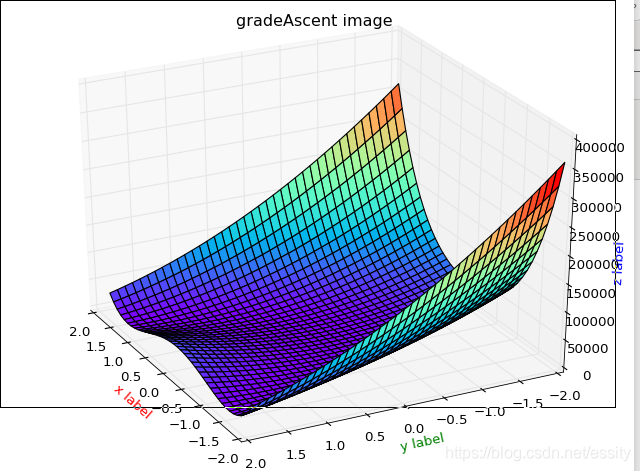
f(x,y)=(1−x)2+100(y−x2)2,使用梯度下降算法求解最小值,函数模型:
模型的代码:
# -*- coding: utf-8 -*-
import numpy as np
from matplotlib import pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from matplotlib import animation as amat
"this function: f(x,y) = (1-x)^2 + 100*(y - x^2)^2"
def Rosenbrock(x, y):
return np.power(1 - x, 2) + np.power(100 * (y - np.power(x, 2)), 2)
def show(X, Y, func=Rosenbrock):
fig = plt.figure()
ax = Axes3D(fig)
X, Y = np.meshgrid(X, Y, sparse=True)
Z = func(X, Y)
plt.title("gradeAscent image")
ax.plot_surface(X, Y, Z, rstride=1, cstride=1, cmap='rainbow', )
ax.set_xlabel('x label', color='r')
ax.set_ylabel('y label', color='g')
ax.set_zlabel('z label', color='b')
amat.FuncAnimation(fig, Rosenbrock, frames=200, interval=20, blit=True)
plt.show()
if __name__ == '__main__':
X = np.arange(-2, 2, 0.1)
Y = np.arange(-2, 2, 0.1)
Z = Rosenbrock(X, Y)
show(X, Y, Rosenbrock)
我们求解出它的梯度方向
g
r
a
d
(
f
(
x
,
y
)
)
=
(
−
2
∗
(
1
−
x
)
−
400
(
y
−
x
∗
x
)
∗
x
grad(f(x,y)) = ( -2*( 1 - x ) -400( y - x*x )*x
grad(f(x,y))=(−2∗(1−x)−400(y−x∗x)∗x,
200
(
y
−
x
∗
x
)
)
200(y - x*x))
200(y−x∗x)) 沿着该梯度的反方向就可以快速确定
x
x
x,
y
y
y 位置的最小点。即最小值
f
(
1
,
1
)
m
i
n
=
0
f(1,1)_{min} = 0
f(1,1)min=0
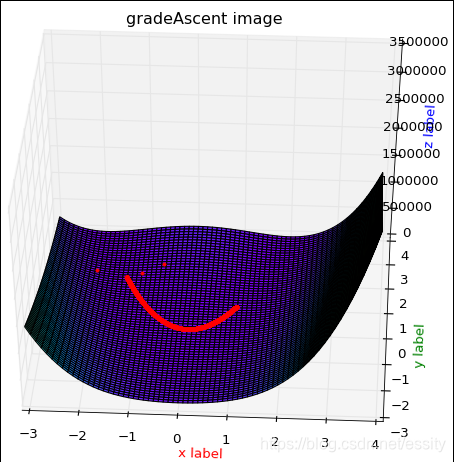
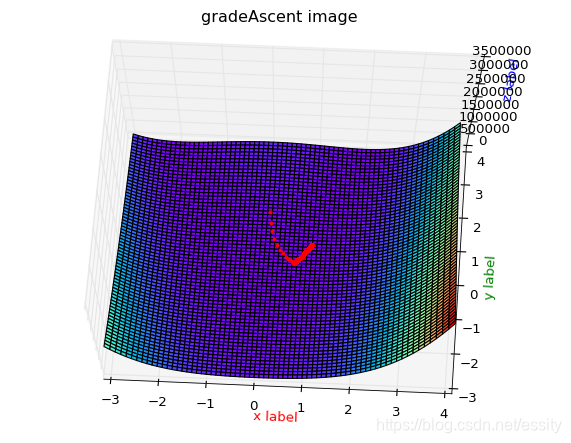
数据变化1:
效果图2:
数据变化截图:
代码:
# -*- coding: utf-8 -*-
import random
import numpy as np
from matplotlib import pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from matplotlib import animation as amat
"this function: f(x,y) = (1-x)^2 + 100*(y - x^2)^2"
def Rosenbrock(x, y):
return np.power(1 - x, 2) + np.power(100 * (y - np.power(x, 2)), 2)
def show(X, Y, func=Rosenbrock):
fig = plt.figure()
ax = Axes3D(fig)
X, Y = np.meshgrid(X, Y, sparse=True)
Z = func(X, Y)
plt.title("gradeAscent image")
ax.plot_surface(X, Y, Z, rstride=1, cstride=1, cmap='rainbow', )
ax.set_xlabel('x label', color='r')
ax.set_ylabel('y label', color='g')
ax.set_zlabel('z label', color='b')
plt.show()
def drawPaht(px, py, pz, X, Y, func=Rosenbrock):
fig = plt.figure()
ax = Axes3D(fig)
X, Y = np.meshgrid(X, Y, sparse=True)
Z = func(X, Y)
plt.title("gradeAscent image")
ax.set_xlabel('x label', color='r')
ax.set_ylabel('y label', color='g')
ax.set_zlabel('z label', color='b')
ax.plot_surface(X, Y, Z, rstride=1, cstride=1, cmap='rainbow', )
ax.plot(px, py, pz, 'r.') # 绘点
plt.show()
def gradeAscent(X, Y, Maxcycles=10000, learnRate=0.0008):
# x, Y = np.meshgrid(X, Y, sparse=True)
new_x = [X]
new_Y = [Y]
g_z=[Rosenbrock(X, Y)]
current_x = X
current_Y = Y
for cycle in range(Maxcycles):
"为了更好的表示grad,我这里对表达式不进行化解"
current_Y -= learnRate * 200 * (Y - X * X)
current_x -= learnRate * (-2 * (1 - X) - 400 * X * (Y - X * X))
X = current_x
Y = current_Y
new_x.append(X)
new_Y.append(Y)
g_z.append(Rosenbrock(X, Y))
return new_x, new_Y, g_z
if __name__ == '__main__':
X = np.arange(-3, 4, 0.1)
Y = np.arange(-3, 4, 0.1)
x = random.uniform(-3, 4)
y = random.uniform(-3, 4)
print x,y
x, y, z = gradeAscent(x, y)
print len(x),x
print len(y),y
print len(z),z
drawPaht(x, y, z, X, Y, Rosenbrock)
5 回归算法
在实际过程中,需要使用电脑处理一些数据的时候,在此过程中,需要找到数据之间的关系,我们会使用生成函数方式来构造一个,我们称之为生成函数,或者母函数或者其他。
电脑处理数据的过程是:需要我们手动给予一个通用表达式,比如线性的,我们需要设定它为
y
=
k
x
+
b
y=kx+b
y=kx+b,然后在给电脑这些数据,告诉它说,这些个数据是线性相关的,你去找到一个
k
,
b
k,b
k,b,使这些点尽可能的满足这个方程吧!而这个过程我们又将它称之为拟合过程。
所以呢?面对一堆数据,而我们给定了一个通用的表达式比如:
h
θ
(
x
)
=
θ
0
+
θ
1
x
1
+
θ
2
x
2
h_\theta(x) = \theta_0+\theta_1x_1+\theta_2x_2
hθ(x)=θ0+θ1x1+θ2x2
其中,
θ
\theta
θ 为每一个特征变量的权重,比如特征
x
1
x_1
x1 的权重为
θ
1
\theta_1
θ1,我们设定
x
0
=
1
x_0=1
x0=1,然后我们将其简化为:
h
(
x
)
=
∑
i
=
0
n
θ
i
x
i
h(x)=\sum_{i=0}^n\theta_ix_i
h(x)=i=0∑nθixi
如果我们在将其转化成多维空间的话,其实可以使用还可以这样:
h
(
x
)
=
∑
i
=
0
n
θ
i
x
i
=
θ
T
x
,
h(x)=\sum_{i=0}^n\theta_ix_i=\theta^Tx,
h(x)=i=0∑nθixi=θTx,
但是到这里,这里依旧还只是一个通试而已,那么我们该如何使用其那些数据呢?
这时候,我们需要来引入一个新的函数,来评估这个通式(我们可以随机给这个式子权重赋值)与实际的值是否在可接收的范围!
但是到这里,这里依旧还只是一个通试而已,那么我们该如何使用其那些数据呢?
这时候,我们需要来引入一个新的函数,来评估这个通式(我们可以随机给这个式子权重赋值)与实际的值是否在可接收的范围!
J
(
θ
)
=
1
2
m
∑
i
=
0
m
(
h
θ
(
x
(
i
)
−
y
(
i
)
)
2
,
J(\theta)=\frac{1}{2m}\sum_{i=0}^{m}(h_\theta(x^{(i)}-y^{(i)})^2,
J(θ)=2m1i=0∑m(hθ(x(i)−y(i))2,
这个函数称谓有两种,一种是损失函数(Loss function),一种是误差函数(Error function)。
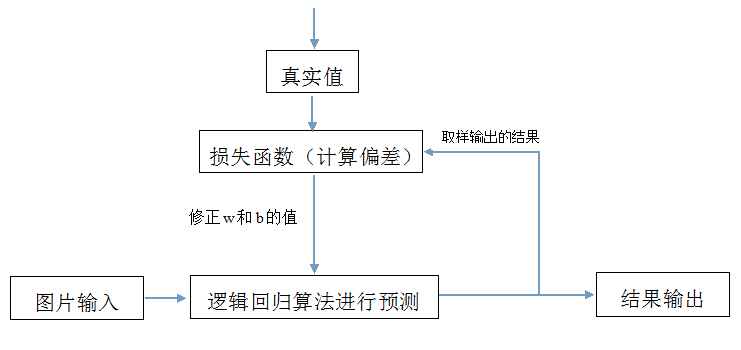
6 逻辑回归算法、损失函数、梯度下降算法之间的关系
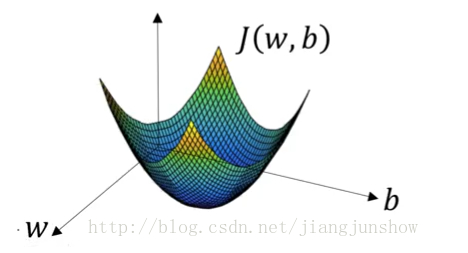
由上面的公式可以看到,损失函数是一个关于w和b的函数。所谓“学习”或“训练神经网络”,就是找到一组最合适的w和b的值,使这个损失函数的值最小,同样也是使逻辑回归算法中w和b的值最合适,进而使预测结果更准确。损失函数的图形如下图所示。
7 批量梯度下降算法(BGD)
然后我们再按照梯度的方向逐步的移动,慢慢的逼近收敛值。用表达式表示为:
θ
j
:
=
θ
j
−
α
∂
∂
θ
j
J
(
θ
)
.
\theta_j := \theta_j - \alpha\frac{\partial}{\partial\theta_j}J(\theta).
θj:=θj−α∂θj∂J(θ).
其中,
α
\alpha
α 表示一个学习率(详解见后文),之所以添加这个学习率,是因为我们使用的是均方差,如果我们随机的方程预测的值与实际的值偏差比较大的话,均方差的值将会非常巨大,这样的话,可能造成我们的这个损失函数出现大幅度的偏移,我们称之为摆钟行为,所以为了避免出现这种情况,这个值就这么的诞生了,这个值的大小,表示每次向着
J
J
J 最陡峭的方向迈步的大小,可以用来调整我们移动的的步子大小。还需要解释的是:
∂
∂
θ
j
J
(
θ
)
\frac{\partial}{\partial\theta_j}J(\theta)
∂θj∂J(θ)
表示的是损失函数的权重梯度,那么对于这个梯度,简化为:
∂
∂
θ
j
J
(
θ
)
=
∂
∂
θ
j
1
2
(
h
θ
(
x
)
−
y
)
2
=
2
∗
1
2
(
h
θ
(
x
)
−
y
)
∗
∂
∂
θ
j
(
h
θ
(
x
)
−
y
)
=
(
h
θ
(
x
)
−
y
)
∗
∂
∂
θ
j
(
∑
i
=
0
n
θ
i
x
i
−
y
)
=
(
h
θ
(
x
)
−
y
)
x
i
\begin{aligned} \frac{\partial}{\partial\theta_j}J(\theta)&=\frac{\partial}{\partial\theta_j}\frac{1}{2}(h_\theta(x)-y)^2 \\ &=2*\frac{1}{2}(h_\theta(x)-y)*\frac{\partial}{\partial\theta_j}(h_\theta(x)-y) \\ &= (h_\theta(x)-y)*\frac{\partial}{\partial\theta_j}(\sum_{i=0}^n\theta_ix_i-y) \\ &= (h_\theta(x)-y)x_i \end{aligned}
∂θj∂J(θ)=∂θj∂21(hθ(x)−y)2=2∗21(hθ(x)−y)∗∂θj∂(hθ(x)−y)=(hθ(x)−y)∗∂θj∂(i=0∑nθixi−y)=(hθ(x)−y)xi
得到上面的推导之后,所以可以用
(
h
θ
(
x
)
−
y
)
x
i
(h_\theta(x)-y)x_i
(hθ(x)−y)xi 替换掉
θ
j
:
=
θ
j
−
α
∂
∂
θ
j
J
(
θ
)
\theta_j := \theta_j - \alpha\frac{\partial}{\partial\theta_j}J(\theta)
θj:=θj−α∂θj∂J(θ) 中的
∂
∂
θ
j
J
(
θ
)
\frac{\partial}{\partial\theta_j}J(\theta)
∂θj∂J(θ),然后得到:
θ
j
:
=
θ
j
+
α
(
y
(
i
)
−
h
θ
(
x
i
)
)
x
j
(
i
)
.
\theta_j := \theta_j+\alpha(y^{(i)}-h_\theta(x^{i}))x_j^{(i)}.
θj:=θj+α(y(i)−hθ(xi))xj(i).
方程中的,
i
i
i 表示的是样本数据中第 i 组训练数据,
j
j
j 其实就是我们的对应的第 j 个权重。伪代码表示:
"这里权重用W表示 , trainingSet 表示训练数据集合 "
for i in range(len(trainingSet)):
"n 表示有多少个特征Xj (j属于[1,n])"
for j in range(n):
w -= a*(yi - h(xi))Xij
而这种方式,是将所有的样本M都参与进去训练,然后得到一个权重值w。这种方式,我们称之为批量梯度下降算法,也就是BGD。
但是这个算法有个缺点,算法时间复杂度为
O
(
n
2
)
O(n^2)
O(n2),当样本量比较大的话,计算量就会变得很大,所以这种方式适用的范围,仅是对那些样本较小的数据而言,对于大数据量样本而言,这个还是不太好的。
8 随机梯度下降算法(SGD)
它的大体思路就是:在给定的样本集合M中,随机取出副本N代替原始样本M来作为全集,对模型进行训练。这种训练由于是抽取部分数据,所以有较大的几率得到的是,一个局部最优解。但是一个明显的好处是,如果在样本抽取合适范围内,既会求出结果,而且速度还快。
9 梯度下降存在的问题
一:参数调整缓慢
梯度下降算法走到接近极小值的时候,由于谷底很平,梯度很小,参数调整会变得缓慢。
在曲线/曲面的平坦区、或者鞍点,也会有这个问题。
二:收敛于局部极小值
没有收敛到全局最小值,只收敛到局部最小值。
10 学习率
对于梯度下降算法,这应该是一个最重要的超参数。如果学习速率设置得非常大,那么训练可能不会收敛,就直接发散了;如果设置的比较小,虽然可以收敛,但是训练时间可能无法接受;如果设置的稍微高一些,训练速度会很快,但是当接近最优点会发生震荡,甚至无法稳定。不同学习速率的选择影响可能非常大,如图:
[外链图片转存失败(img-uwr7xoTL-1563013699045)(https://ss.csdn.net/p?https://mmbiz.qpic.cn/mmbiz_png/iaTa8ut6HiawCqPA5kQ1vBfvWgFicTkRtOaSsic0zzdnwI9I08lfdCbnibWicicslia5LRTDle6PCibibsSpG9McIED8xGUw/0?wx_fmt=png)]
理想的学习速率是:刚开始设置较大,有很快的收敛速度,然后慢慢衰减,保证稳定到达最优点。所以,前面的很多算法都是学习速率自适应的。除此之外,还可以手动实现这样一个自适应过程,如实现学习速率指数式衰减:
η
(
t
)
=
η
0
∗
1
0
−
t
r
\eta(t)=\eta_0*10^{\frac{-t}{r}}
η(t)=η0∗10r−t
在TensorFlow中,你可以这样实现:
initial_learning_rate = 0.1
decay_steps = 10000
decay_rate = 1/10
global_step = tf.Variable(0, trainable=False)
learning_rate = tf.train.exponential_decay(initial_learning_rate,
global_step, decay_steps, decay_rate)
# decayed_learning_rate = learning_rate *
# decay_rate ^ (global_step / decay_steps)
optimizer = tf.train.MomentumOptimizer(learning_rate, momentum=0.9)
training_op = optimizer.minimize(loss, global_step=global_step)
参考文章
【机器学习】代价函数(cost function):https://www.cnblogs.com/Belter/p/6653773.html
学习率(Learning rate)的理解以及如何调整学习率:https://www.cnblogs.com/lliuye/p/9471231.html
深入浅出–梯度下降法及其实现:https://www.jianshu.com/p/c7e642877b0e
关于梯度下降算法的的一些总结:https://www.cnblogs.com/gongxijun/p/5890548.html
最清晰的讲解各种梯度下降法原理与Dropout:https://baijiahao.baidu.com/s?id=1613121229156499765&wfr=spider&for=pc
一文看懂常用的梯度下降算法:https://blog.csdn.net/u013709270/article/details/78667531
动态图和静态图
目前神经网络框架分为静态图框架和动态图框架,PyTorch和TensorFlow、Caffe等框架最大的区别就是他们拥有不同的计算图表现形式。TensorFlow1.*使用静态图(在TensorFlow2.*中使用的是动态图),这意味着我们先定义计算图,然后不断使用它,而在PyTorch中,每次都会重新构建一个新的计算图。
静态图和动态图有各自的优点。动态图比较方便DEBUG,使用者能够使用任何他们喜欢的方式进行debug,同时非常直观,而静态图是通过先定义后运行的方式,之后再次运行的时候就不再需要重新构建计算图,所以速度会比动态图更快。
import torch
from torch.autograd import Variable
x=Variable(torch.randn(1,10))
prev_h=Variable(torch.randn(1,20))
W_h=Variable(torch.randn(20,20))
W_x=Variable(torch.randn(20,10))
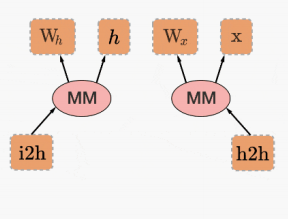
i2h=torch.mm(W_x,x.t())
h2h=torch.mm(W_h,prev_h.t())
比较while循环语句在TensorFlow和PyTorch中的定义。
TensorFlow
import tensorflow as tf
first_counter=tf.constant(0)
second_counter=tf.constant(10)
def cond(first_counter,second_counter,*args):
return first_counter<second_counter
def body(first_counter,second_counter):
first_counter=tf.add(first_counter,2)
second_counter=tf.add(second_counter,1)
return first_counter,second_counter
c1,c2=tf.while_loop(cond,body,[first_counter,second_counter])
with tf.Session() as sess:
counter_1_res,counter_2_res=sess.run([c1,c2])
print(counter_1_res)
print(counter_2_res)
可以看到TensorFlow需要将整个图构成静态的,每次运行的时候图都是一样的,是不能够改变的,所以不能直接使用Python的while循环语句,需要使用辅助函数tf.while_loop写成TensorFlow内部形式。
PyTorch
import torch
first_counter=torch.Tensor([0])
second_counter=torch.Tensor([10])
while(first_counter<second_counter):
first_counter+=2
second_counter+=1
print(first_counter)
print(second_counter)
tensor([20.])
tensor([20.])
可以看到PyTorch的写法和Python的写法是完全一致的,没有任何额外的学习成本。动态图的方式更加简单且直观。