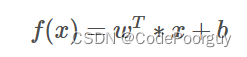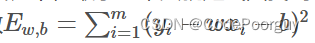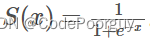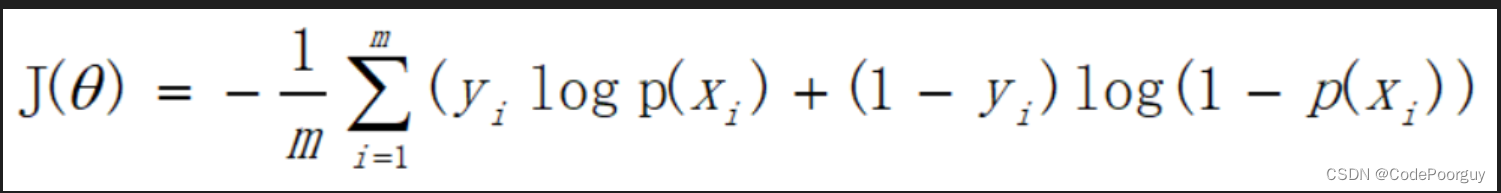提示：文章写完后，目录可以自动生成，如何生成可参考右边的帮助文档

前言

逻辑回归（Logistic Regression）是一种常用的机器学习算法，用于解决分类问题。尽管名字中带有"回归"一词，但逻辑回归实际上是一种分类算法，用于预测实例属于某个类别的概率。在本篇博客中，我们将深入探讨逻辑回归算法的原理、实现和应用。

一、逻辑回归简介

逻辑回归是一种用于解决二分类问题的线性模型。与线性回归不同，逻辑回归不是直接预测数值，而是预测某个实例属于某个类别的概率。通常情况下，逻辑回归的输出值在0到1之间，可以看作是对正类别的预测概率。

二、算法原理

1.线性回归模型

线性回归是一种用于建立特征与连续目标变量之间关系的线性模型的统计学习方法。其目标是找到一条最佳拟合直线（或者更高维的超平面），使得特征和目标变量之间的差异最小化。在线性回归中，通过调整模型参数来最小化数据的残差平方和，从而找到最适合数据的线性关系。

其中，w和b都是通过学习得到的，最常用的方法就是最小二乘法。在线性回归中，最小二乘法就是试图找到一条直线，使得所有样本到直线上的欧氏距离之和最小。我们只需要将函数

求导并令导数为0即可求解出w和b的最优解。

2.sigmoid函数

sigmoid函数是一种常用的数学函数，在机器学习中常用于逻辑回归等模型中作为激活函数使用。它的数学表达式为：

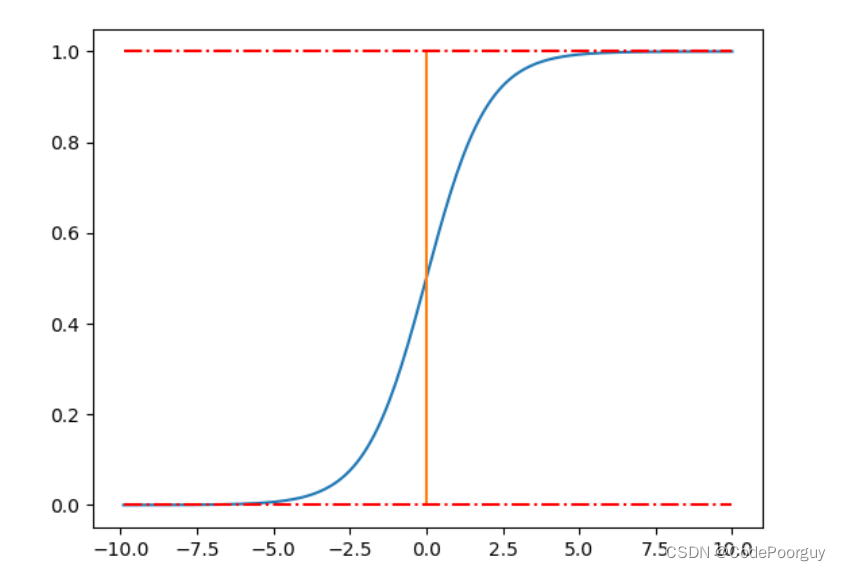
其中，z为输入值。sigmoid函数的输出值范围在0到1之间，具有平滑的S形曲线特点，常用于将输入值映射到概率值。sigmoid函数在神经网络中常被用来在输出层处理二分类问题。

3.梯度的计算

梯度计算是优化算法中的关键步骤，用于求解损失函数对于参数的偏导数，以便更新参数来减小损失函数的值。在逻辑回归等机器学习算法中，梯度计算常用于参数更新的过程中。
逻辑回归中使用的损失函数是交叉熵损失函数，它衡量的是真实标签与预测标签之间的差距。交叉熵损失越小，模型的预测越准确。它的公式为：

损失函数对参数求偏导——>梯度

梯度计算的目标是求解损失函数对于参数向量 w 的偏导数，以便更新参数来减小损失函数。
通过上述公式，我们可以计算出损失函数相对于每个参数的梯度。梯度的值表示损失函数在当前参数取值处的下降速度。

然后，利用梯度下降法或其他优化算法，不断迭代更新参数向量 w，使得损失函数不断减小。
所以，对于逻辑回归问题，我们就是要找到最优的w和b，使得损失函数J（w）最小，在这里，我们使用梯度下降法来求解。

总结起来，梯度计算的原理是求解损失函数对于参数的偏导数，表示损失函数在当前参数取值处的下降速度。

4.梯度下降法

梯度下降法的步骤如下：

# 使用梯度下降法来更新权重
# 初始化权重
# 进行iterations次迭代
    # 计算梯度
    # 更新权重
# 返回更新后的权重.

初始化权重：首先需要对模型的权重进行初始化。

计算梯度：梯度是损失函数关于参数的偏导数，表示损失函数在当前参数取值下的变化方向及速度。通过求解梯度，可以知道在当前参数取值下，应该如何更新参数才能使得损失函数更小。

更新权重：根据梯度信息，使用学习率来控制参数更新的步幅，通过更新规则将参数更新为更优的值。通常使用梯度乘以学习率得到的调整量来更新参数。

重复步骤2和3：重复进行步骤2和3，直到满足指定的停止条件，例如达到最大迭代次数、损失函数几乎不再变化等。每次迭代都会使参数取值向着损失函数更小的方向更新，从而逐步接近损失函数的最小值。

4.优缺点

优点：

简单和高效：逻辑回归是一种线性模型，计算速度快，适合处理大规模数据集。

可解释性强：逻辑回归给出了类别的概率预测，同时可以通过参数的正负和大小来解释特征对分类的影响。

可以处理非线性关系：通过引入高阶项或交互项，逻辑回归能够模拟一定程度的非线性关系。

适用于二分类问题：逻辑回归适用于二分类问题，但也可以通过一些技巧（如一对多）来处理多分类问题。

缺点：

假设线性可分：逻辑回归在建模时假设样本是线性可分的，当数据集存在较复杂的非线性关系时，效果可能不佳。

对异常值敏感：由于逻辑回归使用的是最大似然估计，对于异常值较敏感，异常值的存在可能会导致模型的性能下降。

容易欠拟合：当特征和目标变量之间的关系比较复杂时，逻辑回归可能难以捕捉到所有的特征之间的关联性，容易导致欠拟合。

特征选择的限制：逻辑回归对特征选择的限制较多，对于高维特征空间和特征相关性较强的情况，模型性能可能不佳。

三、代码实现

1.数据集使用

0.406704    7.067335    1
0.667394    12.741452   0
-2.460150   6.866805    1
0.569411    9.548755    0
省略部分......
-0.763693   11.044718   0
-0.025898   1.628767    1

2.数据集预加载

import numpy as np
import matplotlib.pyplot as plt

# 加载数据集
data = np.genfromtxt('D:\L.txt')
X = data[:, :-1]
y = data[:, -1]

使用np.genfromtxt()方法从文件中加载数据集。该方法可以从文本文件中读取数据，并返回一个NumPy数组。

同时将数据分割为2个特征和1个标签

3.参数初始化

# 添加偏置项
X = np.insert(X, 0, 1, axis=1)

# 初始化权重
def initialize_weights(dim):
    return np.zeros(dim)

在逻辑回归中，通常将偏置项作为权重向量的第一个元素，即将其插入特征矩阵的第0列位置。

权重的初始化根据实际需要，可以根据经验设定为全零数组、随机数数组或其他方式。这里采用的是全零数组初始化。

4.实现sigmoid函数

def sigmoid(z):
    return 1 / (1 + np.exp(-z))

sigmoid函数常用于逻辑回归中，用于将线性函数的输出转化为概率形式。值域在[0, 1]之间的sigmoid函数输出，可以表示样本属于某一类别的概率。当输入z趋近于正无穷大时，sigmoid函数趋近于1；当输入z趋近于负无穷大时，sigmoid函数趋近于0。

5.梯度计算

# 计算梯度
def compute_gradient(X, y, weights):
    # 获取数据集大小
    m = len(y)
    # 计算sigmoid函数的输出
    h = sigmoid(np.dot(X, weights))
    # 计算梯度
    gradient = np.dot(X.T, (h - y)) / m
    # 返回梯度
    return gradient

根据给定的特征矩阵X、标签向量y和权重向量weights计算逻辑回归模型的梯度。梯度反映了损失函数关于权重的变化率，可以用于更新权重以最小化损失。

5.梯度下降法

# 使用梯度下降法来更新权重
def gradient_descent(X, y, alpha=0.1, iterations=10000):
    # 初始化权重
    weights = initialize_weights(X.shape[1])
    
    # 进行iterations次迭代
    for _ in range(iterations):
        # 计算梯度
        gradient = compute_gradient(X, y, weights)
        # 更新权重
        weights -= alpha * gradient

    # 返回更新后的权重
    return weights

梯度下降法的核心思想是根据梯度的反方向来更新权重，以找到损失函数的局部最小值。
返回最终更新后的权重weights。

这段代码的功能是通过梯度下降法来更新逻辑回归模型的权重，以达到最小化损失函数的目标。梯度下降法是一种常用的优化算法，通过迭代地沿着梯度的反方向更新权重，逐步减小损失函数的值，从而找到模型的最优解。

6.分类结果绘制

# 绘制分类结果图形
def plot_classification(X, y, weights):
    # 创建图形
    plt.figure()
    # 绘制分类0的点，颜色为红色
    plt.scatter(X[y == 0, 1], X[y == 0, 2], color='red', label='Class 0')
    # 绘制分类1的点，颜色为蓝色
    plt.scatter(X[y == 1, 1], X[y == 1, 2], color='blue', label='Class 1')
    
    # 创建x轴和y轴的最小值和最大值
    x_values = np.array([np.min(X[:, 1]), np.max(X[:, 1])])
                    
    # 根据weights计算y轴值
    y_values = - (weights[0] + weights[1] * x_values) / weights[2]
    
    # 绘制决策边界
    plt.plot(x_values, y_values, label='Decision Boundary')
    
    # 添加x轴和y轴的标签
    plt.xlabel('Feature 1')
    plt.ylabel('Feature 2')
    # 添加图例
    plt.legend()
    # 显示图形
    plt.show()

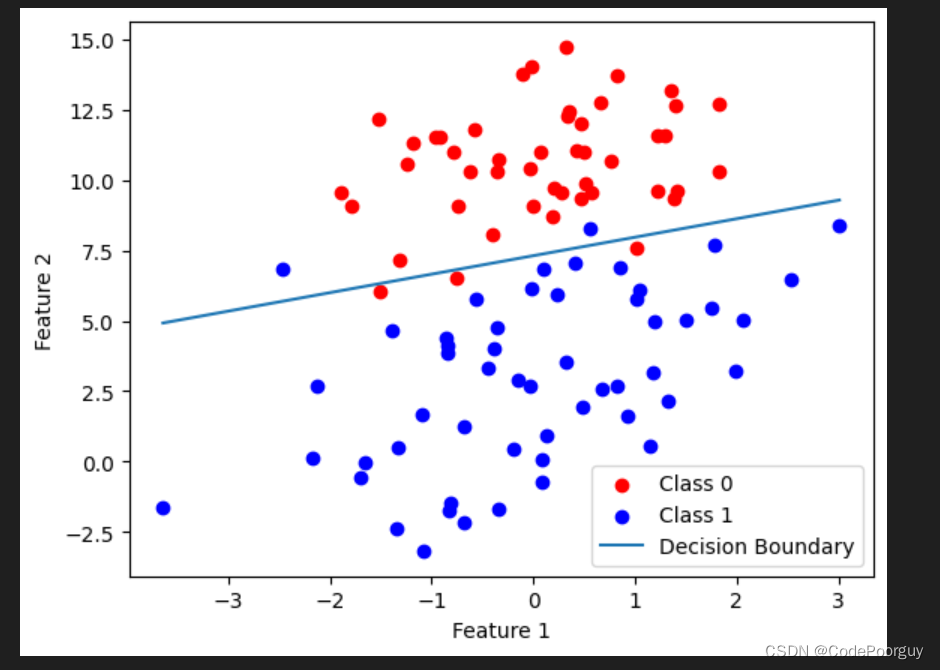
根据逻辑回归模型的权重和特征矩阵X绘制分类结果图形，将标签为0和标签为1的样本点以不同颜色展示，并绘制逻辑回归模型的决策边界。

7.预测函数及主函数

# 定义一个函数，用于预测单个样本
def predict_sample(X_sample, weights):
    # 在输入数据的前面添加一个维度1，以适应矩阵乘法
    X_sample = np.insert(X_sample, 0, 1)
    # 使用训练好的权重参数对输入数据进行计算，然后使用sigmoid函数进行激活
    prediction = sigmoid(np.dot(X_sample, weights))
    # 如果激活值大于等于0.5，则预测结果为1，否则为0
    return 1 if prediction >= 0.5 else 0


# 训练逻辑回归模型
weights = gradient_descent(X, y, alpha=0.01, iterations=100000)
plot_classification(X, y, weights)


# 给定一个新样本
new_label = [1, 0, 1]
new_sample = np.array(new_label)  # 示例新样本，包含两个特征

# 使用训练好的模型进行预测
predicted_class = predict_sample(new_sample, weights)

if predicted_class == 1:
    print("新样本为类别1")
else:
    print("新样本为类别0")

使用逻辑回归模型和权重对单个样本进行二分类预测。根据样本的特征值和权重值，经过计算得到样本属于类别1的概率，然后根据预测概率的阈值（0.5）进行分类预测，将预测结果设为0或1。

最后对新样本的结果进行判断

8.实验结果

由上图可知，本次实验的实验结果错分了5个点。

总结

综上所述，逻辑回归模型通过引入Sigmoid函数，将线性回归的输出转化为概率值，从而实现对二元分类问题的预测。其算法简单且有效，广泛应用于医学、生物统计学、市场营销等领域。尽管面临一些挑战，如对异常值的敏感性和对数据集的特定要求，但通过适当的数据处理和模型调优，逻辑回归仍然是一个非常有力的工具。在未来，随着机器学习和数据科学的发展，逻辑回归及其变种将继续在解决实际问题中发挥重要作用。