前言
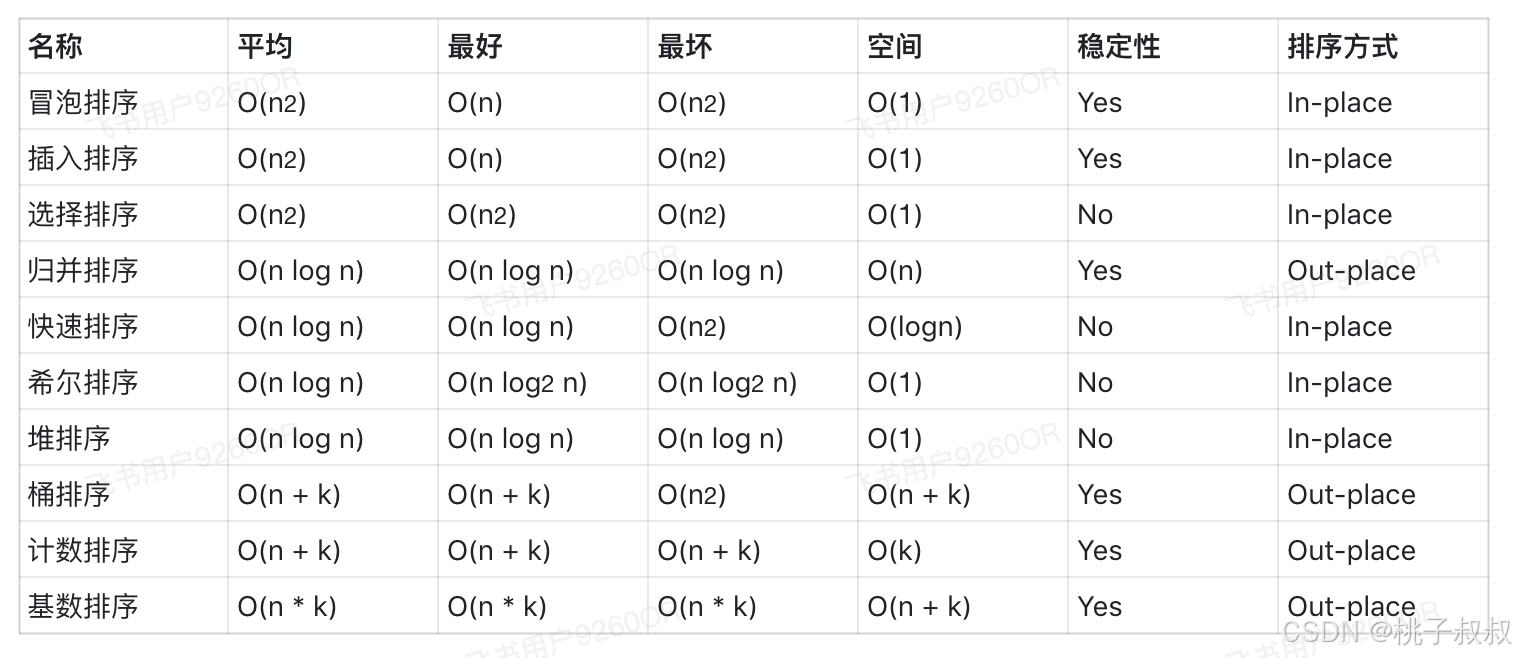
十大经典排序算法的 时间复杂度与空间复杂度 比较。
名词解释:
- n:数据规模;
- k:桶的个数;
- In-place: 占用常数内存,不占用额外内存;
- Out-place: 占用额外内存。
本文主要探讨高频算法排序中的几个常见的冒泡、插入、选择、归并和快速
-
冒泡排序和选择排序是最常见的两种排序,语法简单,容易实现,冒泡排序、插入排序和选择排序虽然在时间复杂度上相对较高,但对于小规模数据或者部分已排序的数据,它们可能更加高效,因为它们的算法简单,不需要额外的内存空间。
-
归并排序和快速排序在平均情况下具有较好的时间复杂度,归并排序的时间复杂度始终为
O(nlogn),快速排序在平均情况下也是O(nlogn),并且它们可以对大规模数据进行高效排序。
有的下盆友会提出疑问,为什么js语法中有了sort函数给数组排序了,为什么还要研究和使用冒泡、插入、选择、归并和快速排序方法?
原因也很简单
sort方法的性能在不同的 JavaScript 引擎中可能有所不同,并且其实现方式通常是比较通用的,不一定针对特定的数据类型或场景进行优化。
例如,对于基本类型数据(如数字)的排序,自定义的快速排序等算法在某些情况下可能比sort方法更快,尤其是对于大规模数据的排序。
对于包含复杂对象的数组,可能需要提供自定义的比较函数,而不同的排序算法在处理自定义比较逻辑时的性能表现也可能不同。
一、排序算法
1、 如何分析一个排序算法
复杂度分析是整个算法学习的精髓。
- 时间复杂度: 一个算法执行所耗费的时间。
- 空间复杂度: 运行完一个程序所需内存的大小。
学习排序算法,我们除了学习它的算法原理、代码实现之外,更重要的是要学会如何评价、分析一个排序算法。
分析一个排序算法,要从 执行效率、内存消耗、稳定性 三方面入手。
2、执行效率
- 最好情况、最坏情况、平均情况时间复杂度
我们在分析排序算法的时间复杂度时,要分别给出最好情况、最坏情况、平均情况下的时间复杂度。
除此之外,你还要说出最好、最坏时间复杂度对应的要排序的原始数据是什么样的。 - 时间复杂度的系数、常数 、低阶
我们知道,时间复杂度反应的是数据规模 n 很大的时候的一个增长趋势,所以它表示的时候会忽略系数、常数、低阶。
但是实际的软件开发中,我们排序的可能是 10 个、100 个、1000 个这样规模很小的数据,所以,在对同一阶时间复杂度的排序算法性能对比的时候,我们就要把系数、常数、低阶也考虑进来。 - 比较次数和交换(或移动)次数
基于比较的排序算法的执行过程,会涉及两种操作,一种是元素比较大小,另一种是元素交换或移动。
所以,如果我们在分析排序算法的执行效率的时候,应该把比较次数和交换(或移动)次数也考虑进去。
3、内存消耗
也就是看空间复杂度。
还需要知道如下术语:
- 内排序:所有排序操作都在内存中完成;
- 外排序:由于数据太大,因此把数据放在磁盘中,而排序通过磁盘和内存的数据传输才能进行;
- 原地排序:原地排序算法,就是特指空间复杂度是 O(1) 的排序算法。
4、稳定性
- 稳定:如果待排序的序列中存在值相等的元素,经过排序之后,相等元素之间原有的先后顺序不变。
比如: a 原本在 b 前面,而 a = b,排序之后,a 仍然在 b 的前面; - 不稳定:如果待排序的序列中存在值相等的元素,经过排序之后,相等元素之间原有的先后顺序改变。
比如:a 原本在 b 的前面,而 a = b,排序之后, a 在 b 的后面;
二、冒泡排序(Bubble Sort)
1、思想
- 冒泡排序只会操作相邻的两个数据。
- 每次冒泡操作都会对相邻的两个元素进行比较,看是否满足大小关系要求。如果不满足就让它俩互换。
- 一次冒泡会让至少一个元素移动到它应该在的位置,重复 n 次,就完成了 n 个数据的排序工作。
2、特点
- 优点:排序算法的基础,简单实用易于理解。
- 缺点:比较次数多,效率较低。
3、实现
// 冒泡排序(已优化)
const bubbleSort2 = arr => {
console.time('改进后冒泡排序耗时');
const length = arr.length;
if (length <= 1) return;
// i < length - 1 是因为外层只需要 length-1 次就排好了,第 length 次比较是多余的。
for (let i = 0; i < length - 1; i++) {
let hasChange = false; // 提前退出冒泡循环的标志位
// j < length - i - 1 是因为内层的 length-i-1 到 length-1 的位置已经排好了,不需要再比较一次。
for (let j = 0; j < length - i - 1; j++) {
if (arr[j] > arr[j + 1]) {
const temp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = temp;
hasChange = true; // 表示有数据交换
}
}
if (!hasChange) break; // 如果 false 说明所有元素已经到位,没有数据交换,提前退出
}
console.log('改进后 arr :', arr);
console.timeEnd('改进后冒泡排序耗时');
};
上面代码中通过参数hasChange进行了优化:当某次冒泡操作已经没有数据交换时,说明已经达到完全有序,不用再继续执行后续的冒泡操作。
4、冒泡排序的时间复杂度是多少 ?
最佳情况:T(n) = O(n),当数据已经是正序时。
最差情况:T(n) = O(n(2)),当数据是反序时。
平均情况:T(n) = O(n(2))。
三、插入排序
插入排序又为分为 直接插入排序 和优化后的 拆半插入排序 与 希尔排序(下文讲),我们通常说的插入排序是指直接插入排序。
1、思想
一般人打扑克牌,整理牌的时候,都是按牌的大小(从小到大或者从大到小)整理牌的,那每摸一张新牌,就扫描自己的牌,把新牌插入到相应的位置。
插入排序的工作原理:通过构建有序序列,对于未排序数据,在已排序序列中从后向前扫描,找到相应位置并插入。
2、步骤
- 从第一个元素开始,该元素可以认为已经被排序;
- 取出下一个元素,在已经排序的元素序列中从后向前扫描;
- 如果该元素(已排序)大于新元素,将该元素移到下一位置;
- 重复步骤 3,直到找到已排序的元素小于或者等于新元素的位置;
- 将新元素插入到该位置后;
- 重复步骤 2 ~ 5。
3、实现
// 插入排序
const insertionSort = array => {
const len = array.length;
if (len <= 1) return
let preIndex, current;
for (let i = 1; i < len; i++) {
preIndex = i - 1; //待比较元素的下标
current = array[i]; //当前元素
while (preIndex >= 0 && array[preIndex] > current) {
//前置条件之一: 待比较元素比当前元素大
array[preIndex + 1] = array[preIndex]; //将待比较元素后移一位
preIndex--; //游标前移一位
}
if (preIndex + 1 != i) {
//避免同一个元素赋值给自身
array[preIndex + 1] = current; //将当前元素插入预留空位
console.log('array :', array);
}
}
return array;
};
4、插入排序的时间复杂度是多少 ?
最佳情况:T(n) = O(n),当数据已经是正序时。
最差情况:T(n) = O(n(2)),当数据是反序时。
平均情况:T(n) = O(n(2))。
四、选择排序
冒泡排序和选择排序是最常见的两种排序,语法简单,容易实现,冒泡排序、插入排序和选择排序虽然在时间复杂度上相对较高,但对于小规模数据或者部分已排序的数据,它们可能更加高效,因为它们的算法简单,不需要额外的内存空间。
1、思路
选择排序算法的实现思路有点类似插入排序,也分已排序区间和未排序区间。但是选择排序每次会从未排序区间中找到最小的元素,将其放到已排序区间的末尾。
2、步骤
- 首先在未排序序列中找到最小(大)元素,存放到排序序列的起始位置。
- 再从剩余未排序元素中继续寻找最小(大)元素,然后放到已排序序列的末尾。
- 重复第二步,直到所有元素均排序完毕。
3、实现
const selectionSort = array => {
const len = array.length;
let minIndex, temp;
for (let i = 0; i < len - 1; i++) {
minIndex = i;
for (let j = i + 1; j < len; j++) {
if (array[j] < array[minIndex]) {
// 寻找最小的数
minIndex = j; // 将最小数的索引保存
}
}
temp = array[i];
array[i] = array[minIndex];
array[minIndex] = temp;
console.log('array: ', array);
}
return array;
};
4、选择排序的时间复杂度是多少 ?
无论是正序还是逆序,选择排序都会遍历 n(2) / 2 次来排序,所以,最佳、最差和平均的复杂度是一样的。
最佳情况:T(n) = O(n(2))。
最差情况:T(n) = O(n(2))。
平均情况:T(n) = O(n(2))。
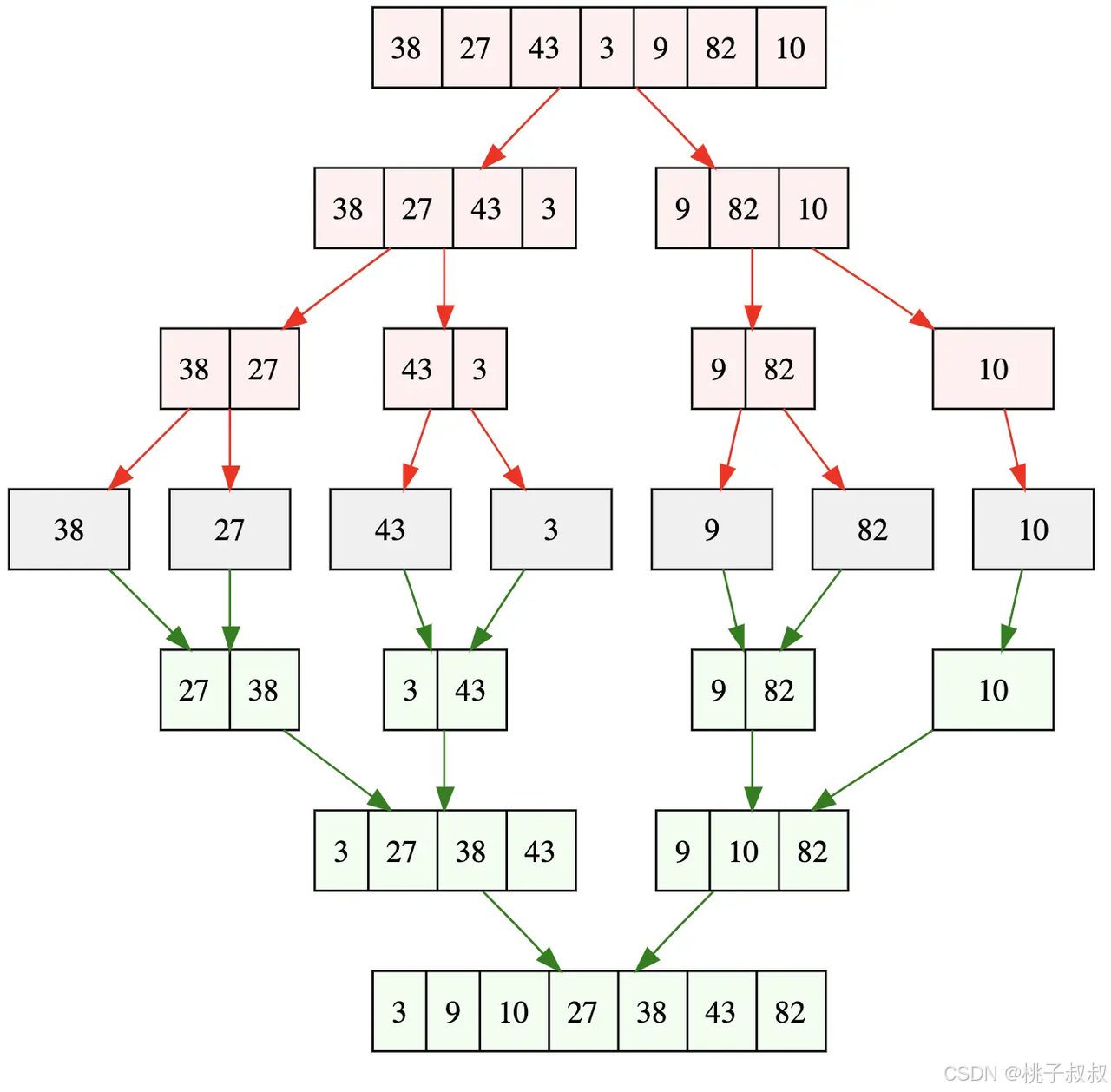
五、归并排序
归并排序采用的是分治思想。
分治,顾名思义,就是分而治之,将一个大问题分解成小的子问题来解决。小的子问题解决了,大问题也就解决了。
1、归并排序有以下优点:
1. 时间复杂度稳定
归并排序的时间复杂度始终为(O(n log n)),其中(n)是待排序数组的长度。无论输入数据的初始状态如何,归并排序都能在相对较短的时间内完成排序任务。这使得它在处理大规模数据时非常高效,不会因为数据的特殊分布而导致性能急剧下降。
相比一些时间复杂度较差的排序算法(如冒泡排序、选择排序、插入排序的平均和最差时间复杂度为O(n^2)),归并排序的效率更高。
2. 稳定排序
归并排序是一种稳定的排序算法。这意味着当对包含相等元素的数组进行排序时,相等元素的相对顺序在排序前后保持不变。在某些应用场景中,数据的相对顺序具有重要意义,归并排序的稳定性就显得尤为重要。
3.适用于外部排序
对于非常大的数据集,可能无法一次性加载到内存中进行排序。归并排序可以很容易地应用于外部排序,即将数据分成较小的块进行排序,然后逐步合并这些已排序的块。这种方法可以有效地处理超出内存容量的大数据集。
4. 易于并行化
归并排序的分治策略使其易于并行化。可以将不同的子问题分配给不同的处理器或线程进行处理,然后再将结果合并。在现代多核处理器和分布式计算环境中,这一特性可以大大提高排序的效率。
5. 适用于多种数据类型
归并排序可以应用于各种数据类型,包括基本数据类型(如整数、浮点数等)和复杂的数据结构(如对象、结构体等)。只需要定义合适的比较函数,就可以对不同类型的数据进行排序。
2、代码实现
const mergeSort = arr => {
//采用自上而下的递归方法
const len = arr.length;
if (len < 2) {
return arr;
}
// length >> 1 和 Math.floor(len / 2) 等价
let middle = Math.floor(len / 2),
left = arr.slice(0, middle),
right = arr.slice(middle); // 拆分为两个子数组
return merge(mergeSort(left), mergeSort(right));
};
const merge = (left, right) => {
const result = [];
while (left.length && right.length) {
// 注意: 判断的条件是小于或等于,如果只是小于,那么排序将不稳定.
if (left[0] <= right[0]) {
result.push(left.shift());
} else {
result.push(right.shift());
}
}
while (left.length) result.push(left.shift());
while (right.length) result.push(right.shift());
return result;
};
六、快速排序 (Quick Sort)
快速排序的特点就是快,而且效率高!它是处理大数据最快的排序算法之一。
1、思想
- 先找到一个基准点(一般指数组的中部),然后数组被该基准点分为两部分,依次与该基准点数据比较,如果比它小,放左边;反之,放右边。
- 左右分别用一个空数组去存储比较后的数据。
- 最后递归执行上述操作,直到数组长度 <= 1;
2、特点:
快速,常用。
3、缺点:
(1)需要另外声明两个数组,浪费了内存空间资源。
(2)快速排序是一种不稳定的排序算法。这意味着在排序过程中,相等元素的相对顺序可能会发生改变。在某些对稳定性有要求的场景中,这可能是一个缺点。
4、实现
const quickSort1 = arr => {
if (arr.length <= 1) {
return arr;
}
//取基准点
const midIndex = Math.floor(arr.length / 2);
//取基准点的值,splice(index,1) 则返回的是含有被删除的元素的数组。
const valArr = arr.splice(midIndex, 1);
const midIndexVal = valArr[0];
const left = []; //存放比基准点小的数组
const right = []; //存放比基准点大的数组
//遍历数组,进行判断分配
for (let i = 0; i < arr.length; i++) {
if (arr[i] < midIndexVal) {
left.push(arr[i]); //比基准点小的放在左边数组
} else {
right.push(arr[i]); //比基准点大的放在右边数组
}
}
//递归执行以上操作,对左右两个数组进行操作,直到数组长度为 <= 1
return quickSort1(left).concat(midIndexVal, quickSort1(right));
};
const array2 = [5, 4, 3, 2, 1];
console.log('quickSort1 ', quickSort1(array2));
// quickSort1: [1, 2, 3, 4, 5]
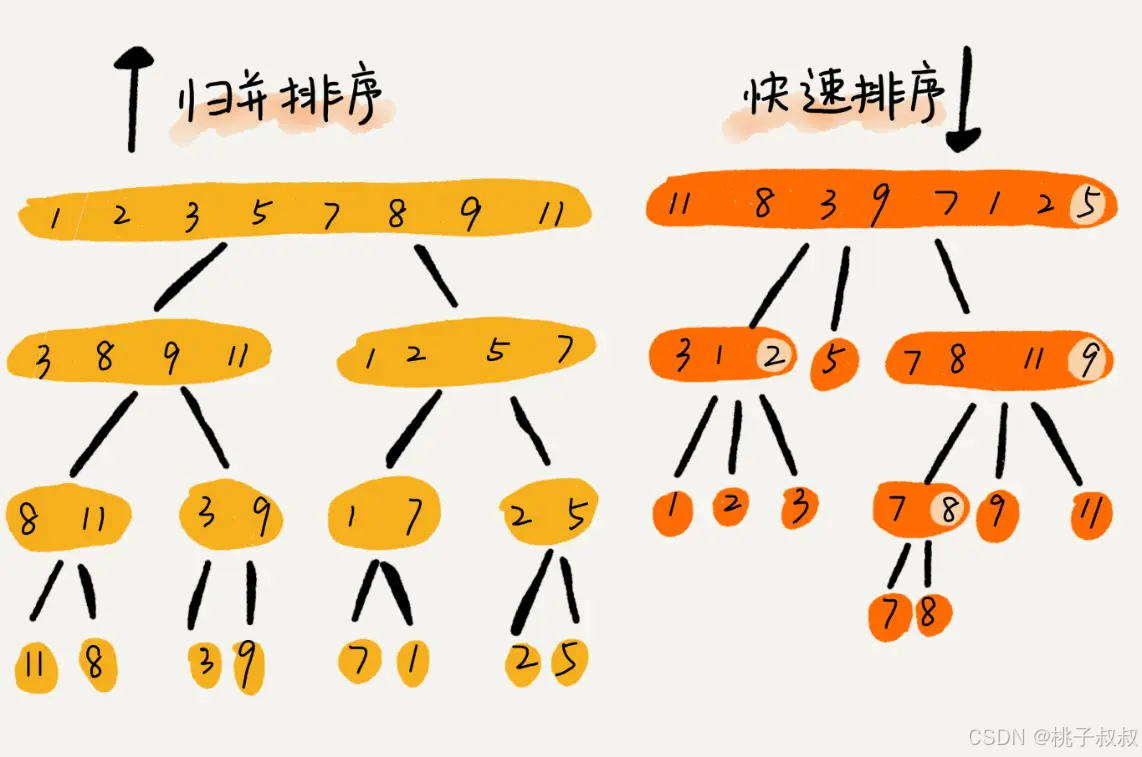
七、 归并排序和快速排序的区别
- 归并排序的处理过程是由下而上的,先处理子问题,然后再合并。
- 而快排正好相反,它的处理过程是由上而下的,先分区,然后再处理子问题。
- 归并排序虽然是稳定的、时间复杂度为 O(nlogn) 的排序算法,但是它是非原地排序算法。
- 归并之所以是非原地排序算法,主要原因是合并函数无法在原地执行。
- 快速排序通过设计巧妙的原地分区函数,可以实现原地排序,解决了归并排序占用太多内存的问题。