数据结构复习之线性表

开始之前，先说下，概述的一个比较重要的考点，时间复杂度的计算步骤？这点在软考中其实是总结过的，详见《软考考点之如何估算一个算法的时间复杂度和空间复杂度》
再次说下要点：1、找出最基本的语句，关键就看这个基本语句的循环的次数阶 2、找到基本语句大体的阶即可。没有必要太精确。3、对应到时间复杂度的数量级即可。时间复杂度按数量级递增排列依次为：常数阶O（1）、对数阶O（log2n）、线性阶O（n）、线性对数阶O（nlog2n）、平方阶O（n^2 ）、立方阶 ( O^3 ）、……k次方阶O（n^k ）、指数阶O（2^n）、阶乘n!.
软考考点之如何估算一个算法的时间复杂度和空间复杂度

什么是线性表呢？

指的是逻辑结构，n个数据元素(结点)a1，a2，…，an组成的有限序列，记为(a1，a2，…，ai-1，ai，ai+1，…，an)。
单纯从上面的定义，还是比较模糊，从其非空线性表特征上，可以明确了回答上面问题，如下：
①. 有且仅有一个称为开始元素的a1，它没有前趋，仅有一个直接后继a2；
②. 有且仅有一个称为终端元素的an，它没有后继，仅有一个直接前趋；
③. 其余元素ai(2≤i≤n-1)称为内部元素，它们都有且仅有一个直接前趋ai-1和一个直接后继ai+1

基本运算？？

(1)置空表 InitList(L)，构造一个空的线性表L。
(2)求表长ListLength(L)，返回线性表L中元素个数，即求的表长。
(3)取表中第i个元素GetNode(L，i)，若1≤i≤ListLength(L)，则返回第i个元素ai。
(4)按值查找LocateNode(L，x)，在表L中查找第一个值为x的元素，并返回该元素在表L中的位置，若表中没有元素的值为x，则返回0值。
(5)插入InsertList(L，i，x)，在表L的第i元素之前插入一个值为x的新元素，表L的长度加1
(6)删除DeleteList(L，i)，删除表L的第i个元素，表L的长度减1。
实际遇到的复杂运算可以由有各种基本运算组合实现。

线性表的顺序存储？

数据元素按其逻辑次序依次存入一组地址连续的（也就是在物理上或计算机里也是连续的）存储单元里，也就是顺序表,c中用一维数组来表示这样的结构。已知第一个无素的地址，可通过公式 Loc（ai）= Loc（a1）+（i-1）*d求任意结点的物理空间地址。

顺序表的数据结构定义

#define MAXSIZE 10
typedef int DataType;
typedef int status;
typedef struct
{
 DataType listData[MAXSIZE];
 int listLen;//实际存储的元素个数
}SeqListType;

基本运算的算法实现：

插入：

算法实现：
插入时一定是从最后一元素legth-1到第i-1个元素依次向后移（腾位置）这里要注意为什么都是-1的位置呢？算法是用c实现的，c中数组是从0开始的所以从哪个位置开始其实是-1的位置.

     /**
      * @name:
      * @test: 在某个位置前插入到顺序表
      * @msg:
      * @param {SeqListType} *sl 顺序表指针
      * @param {int} n 插入的位置，从1开始数
      * @param {int} data 插入的数
      * @return {*}成功返回1，失败返回0
      */
     int SeqListInsert(SeqListType *sl, int n, DataType data) {
         if (sl->listLen > MAXSIZE) {
             printf("the order sheet is full\n");
             return 0;
         }
         if (n < 1 || n > sl->listLen + 1) {  // n是从1开始，所以肯定不能小于1，可以插到最后一个
                                              //位置listLen之后，即lenList+1,但大于这个位置就
                                              //有错误了。
             printf("the postion error\n");
             return 0;
         }
     
         for (int j = sl->listLen - 1; j > n - 1; j--) {  //这里就要操作数组了，数组是从0开始的，所以
                                                          //从最后一个元素到插入位置依次往后移一位
             sl->listData[j + 1] = sl->listData[j];
         }
     
         //移完之后，插入数值就可以了
         sl->listData[n - 1] = data;
         sl->listLen++;  //实际表长加1
         return 1;
     }

删除：

步骤是从第i到最后一个元素legth-1,依次往前赋值。i就是实际i位置的下一元素的下标，这里指数组里的下标表示。最后把数组长度减减。

算法实现：

/**
* @name:
* @test: test font
* @msg:
* @param {SeqListType} *sl
* @param {int} n 删除的位置，也是从1开始
* @return {*}删除成功返回被删除的值
*/
DataType SeqListDelete(SeqListType *sl, int n) {
 if (n < 1 || n > sl->listLen) {
     printf("position error\n");
     exit(0);
 }
 DataType x = sl->listData[n-1];
 for (int i = n; i <= sl->listLen - 1; i++) {
     sl->listData[i - 1] = sl->listData[i];
 }
 sl->listLen--;
 return x;
}

运算算法分析：

插入：

① 合法的插入位置共n+1个，即第1个位置到到第n+1个位置。
② 最坏情况是插入到第1个位置，共需要移动n个元素。故插入算法的最坏情况时间复杂性是O（n）。
③ 最好情况是插入到第n+1个位置，不需要移动元素。
④ 在插入位置等概率情况下，平均移动元素的个数为：（n +（n - 1）+（n -2）+ …+ 2 + 1+0）/（n+1）= n / 2。故插入算法平均时间复杂性是O（n）。

删除：

① 合法的删除位置共n个，即第1个位置到第n个位置。
② 最坏情况是删除第1个位置上的元素，共需要移动n-1个元素。故插入算法的最坏情况时间复杂性是O（n）。
③ 最好情况是删除第n个位置上的元素，不需要移动元素。
④ 在删除元素的位置等概率情况下，平均移动元素的个数为：（（n-1）+（n -2）+ … + 2 + 1+0）/ n=（n - 1）/ 2。故删除算法平均时间复杂性是O（n）。

线性表的链式存储结构？

单链表:

由结点数据域和结点指针域两部分组成。逻辑次序与存储次序不一定相同，通过指针来反映结点间的逻辑关系。

单链表数据结构定义：

typedef int ElemType;

typedef struct Node {
    ElemType date;
    struct Node* next;
} ListNode;

typedef  ListNode* LinkList;  //定义指向链表的指针
ListNode *p;//定义一个指向结点的指针变量
LinkList head;//定义指向单链表的头指针

单链表基本运算：非常重要的考点

动态建立单链表：

头插法：

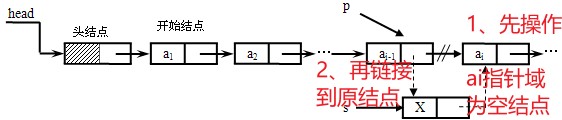
从一个空表开始，重复读入数据，生成新结点，将读入的数据存放到新结点的数据域中，然后将新结点插入到当前链表的表头上，直到读入结束标志为止。如图：

在这里插入图片描述
算法实现，还是符合，指针在表达式左面就是指针，表达式右面就是结点的规律。

LinkList InsertHead(LinkList l, ElemType data)
{
  LinkList head;
  ListNode *p;
  char ch;
  head = NULL; //置空单链表
  ch = getchar();
  while (ch != '\n') {
      p = (ListNode *)malloc(sizeof(ListNode));//申请一个新的结点
      p->data = ch; //将读入的值 赋给数据域
      p->next = head; //新申请的结点指针域指向谁呢？应该指向最头的结点，最头的结点用head标识
      head = p; //此时，最头结点变了，所以要把最头结点指针，指向新插入的结点
      ch = getchar(); //读下一个字符
  }
  return head;
}

尾插法：

先把p赋给rear的next,然后把p结点的指针域填空，最后把rear指向最后一个结点。在空链表时，还需要一个head指针。如图：

在这里插入图片描述
算法实现

LinkList InsertRear()
{
  LinkList head，rear;
  ListNode *p;
  char ch;
  head = NULL;
  rear = NULL; //置空单链表
  ch = getchar(); //读入第一个字符
  while (ch != '\n') { //读入字符不是结束标志符时作循环
      p = (ListNode *)malloc(Sizeof(ListNode)); //申请新结点
      p->data = ch; //数据域赋值
      if (head == NULL) head = p; //空表，head指向p
      else rear->next = p; //新结点*p插入到非空表的表尾结点*rear之后
      rear = p; //表尾变了，更新表尾为新插入的结点
      ch = getchar(); //读入下一个字符
  }
  if (rear != NULL) rear->next = NULL; //最尾结点存在，将尾结点指针域清空
  return head;
}

带头结点的尾插法：

所谓简化单链表主要是指引入头结点后，不再判断是否是从空开始连接，如下图带头结点尾插法：在这里插入图片描述
算法实现

LinkList InsertRearH() //这里的头结点是一个数据域为空的结点,起到标识的作用,注意与头指针不同,名字是不一样的,但作用差不多
{
    LinkList head = (ListNode *)malloc(Sizeof(ListNode)); //申请头结点
    ListNode *p，*rear;
    DataType ch;
    rear = head; //最尾结点为头结点,此时其实是空表
    while ((ch = getchar()) != '\n') {
        p = (ListNode *)malloc(sizeof(ListNode)); //申请新结点
        p->data = ch;
        rear->next = p; //最尾结点指针域指向新插入结点
        rear = p; //更新尾指针
    }
    rear->next = NULL; //终端结点指针域置空
    return head;
}

查找算法：

查找位号为i的结点

ListNode *GetNodei(LinkList head，int i)
{
    //head为带头结点的单链表的头指针，i为要查找的结点序号
    ListNode *p;
    int j;
    p = head->next;//因为是带头结点，所以头指针->next，表示的是第一个结点
    j = 1; //j表示位号
    while (p != NULL && j < i) { //顺指针向后查找，直到p指向第i个结点或p为空为止
        p = p->next;
        ++j;
    }
    if (j == i) //若查找成功，则返回查找结点的存储地址(位置)，否则返回NULL
        return p;
    else
        return NULL;
}

查找值为k的元素

LiStNode *LocateNodek(LinkList head，DataType k)
{
    //head为带头结点的单链表的头指针，k为要查找的结点值
    ListNode *p = head->next; //p指向真正的第一个结点
    while (p && p->data != k) //循环直到p等于NULL或p->data等于k为止
        p = p->next; //指针指向下一个结点
    return p; //若找到值为k的结点，则p指向该结点，否则p为NULL
}

算法分析

时间复杂度都是O(n)

插入算法：

先使p指向ai-1的位置，然后生成一个数据域值为x的新结点*s，再进行插入操作,如图：在这里插入图片描述

算法实现：

void InsertList(LinkList head, int i, DataType X)
{
//在以head为头指针的带头结点的单链表中第i个结点的位置上
//插入一个数据域值为X的新结点
    ListNode *p, *s;
    int j;
    p = head;
    j = 0;
    while (p != NULL && j < i - 1) { //使p指向第i-1个结点
        p = p->next;
        ++j;
    }
    if (p == NULL) { //N入位置错误,i-1位置就是最后一个结点
        printf("ERROR\n");//个人觉得这里不这样写也可以，反正就是在最后面插入
        return;
    } else {
        s = (ListNode *)malloc(Sizeof(ListNode));//申请新结点
        s->data = X;
        s->next = p->next;//新申请的结点指针域，指向i-1的下一个结点
        p->next = s;//i-1的指针域指向新申请的结点
    }
}

删除运算：

先使p指向ai-1的位置，然后执行p->next指向第i+1个结点，再将第i个结点释放掉。如图：在这里插入图片描述
算法实现：

DataType DeleteList(LinkList head, int i)
{
    //在以head为头指针的带头结点的单链表中删除第i个结点
    ListNode *p, *s;
    dataType x;
    int j;
    p = head;
    j = 0;
    while (p != NULL && j < i - 1) { //使p指向第i-1个结点
        p = p->next j++;
    }
    if (p == NULL) { //删除位置错误
        printf("位置错误\n");
        exit(0); //出错退出处理
    } else {
        s = p->next; //s指向第i个结点
        p->next = s->next; //使i-1的指针域指向i+1
        x = s->data; //保存被删除结点的值
        free(s);
        return x; //删除第i个结点,返回结点值
    }
}

单循环链表：

与单链表区别

最后一个结点的指针域不再为NULL,而是指向头结点。

优点：

可以从任意结点出发，遍历链表。
将头指针改为尾指针rear,头结点rear–>next,开始结点rear–>next–>next,尾结点rear

基本运算

详见数据结构考点之链表算法整理里关于单链表操作部分

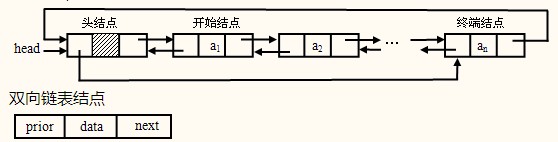
双向循环链表：

在这里插入图片描述

每个结点有两上指针域，分别指向直接前驱和后继。

对称性：

双链表结构是一种对称结构，既有前向链，又有后向链，这就使得插入操作及删除操作都非常方便。

p->prior ->next == p->next->prior == p

数据结构表示

typedef struct dlnode
{
    DataType data;
    struct dlnode *prior, *next;
} DLNode; //双向链表结点的类型定义
typedef DLNode *DLinkList;
DlinkList head; //head为指向双向链表的指针

基本运算

在双链表上实现求表长、按序号查找、定位、插入和删除等运算与单链表上的实现方法基本相同，不同的主要是插入和删除操作。

删除操作：

如图: 在这里插入图片描述
① p ->prior ->next=p->next；② p ->next ->prior=p->prior；

算法实现

DataType DLDelete(DLNode *p)
{
    //删除带头结点的双向链表中指定结点*p
    p->prior->next = p->next;
    p->next->prior = p->prior; //上面两条语句的顺序可以调换，不影响操作结果。
    x = p->data;
    free(p);
    return x;
}

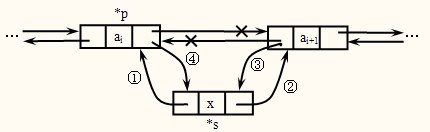
插入操作：

前插操作

如图：
在这里插入图片描述

前插算法实现

void DLInsertF(DLNode *p，DataType x)
{
    //将值为x的新结点插入到带头结点的双向链表中指定结点*p之前
    DLNode *s = (DLNode *)malloc(sizeof(DLNode)); //申请新结点
    s->data = x;
    s->prior = p->prior; //完成①步操作
    s->next = p; //完成②步操作
    p->prior->next = s; //完成③步操作
    p->prior = s; //完成④步操作
}

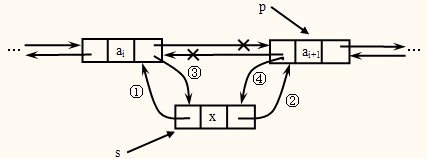
后插操作

如图：
在这里插入图片描述
① s->prior= p； ② s->next=p->next；
③ p->next->prior=s； ④ p->next=s；

后插算法实现

void DLInsertB(DLNode *p，DataType x)
{
    //将值为x的新结点插入到带头结点的双向链表中指定结点*p之后
    DLNode *s = (DLNode *)malloc(sizeof(DLNode)); //申请新结点
    s->data = x;
    s->prior = p; //完成①步操作
    s->next = p->next; //完成②步操作
    p->next->prior = s; //完成③步操作
    p->next = s; //完成④步操作,③与④顺序不能调换，若先操作p->next,则3步中的p->显然已经变化了
}
//与下面的四步等同，也可以实现后插操作
① s->prior=p； ② s->next=p->next；
③ p->next=s； ④ s->next->prior=s；

顺序表和链表比较：

①对线性表的操作是经常性的查找运算，以顺序表形式存储为宜。因为顺序存储可以随机访问任一结点，访问每个结点的复杂度均为O (1)。而链式存储结构必须从表头开始沿链逐一访问各结点，其时间复杂度为O (n)。
②如果经常进行的运算是插入和删除运算，以链式存储结构为宜。因为顺序表作插入和删除操作需要移动大量结点，而链式结构只需要修改相应的指针。
③对于线性表结点的存储密度问题，也是选择存储结构的一个重要依据。所谓存储密度就是结点空间的利用率。它的计算公式为
存储密度=(结点数据域所占空间)／(整个结点所占空间)
结点存储密度越大，存储空间的利用率就越高。