一、 Antialiasing (反走样)
1. Sampling theory (采样原理)
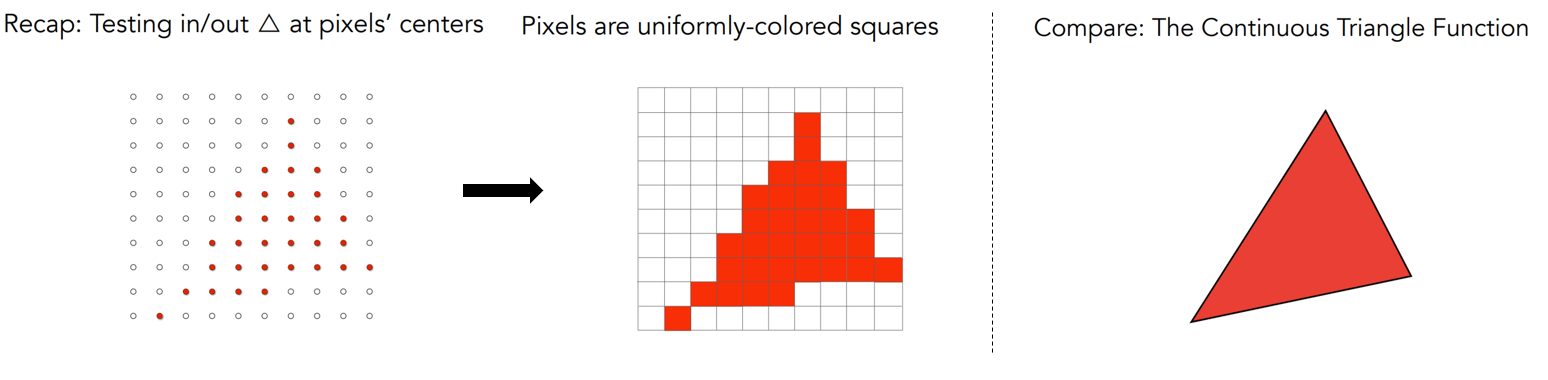
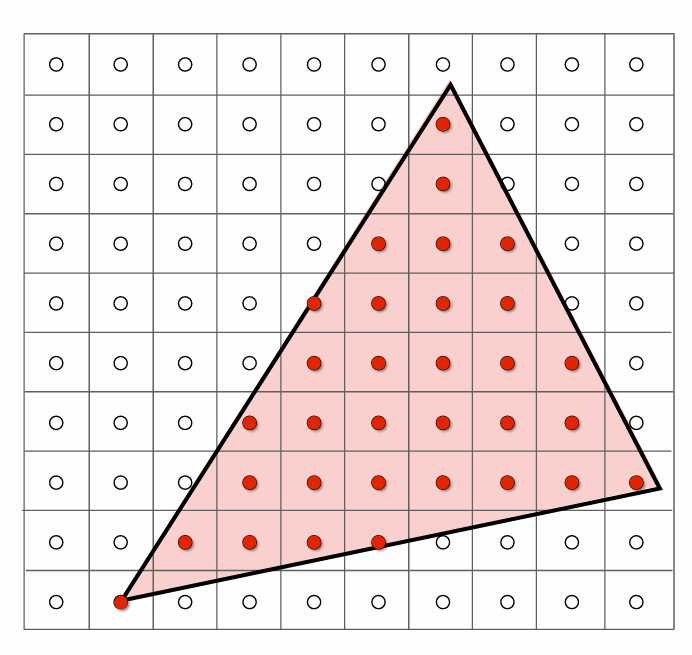
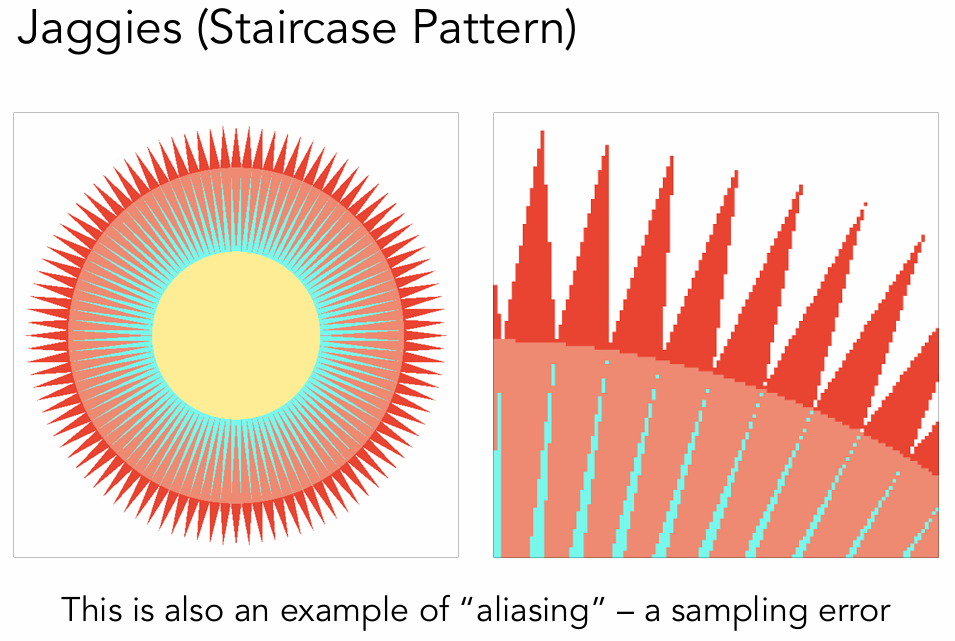
在上一讲我们做完采样工作以后,得到了如下图左边的图片,将所有红点所在的像素填充颜色后,我们得到了中间的图片,但是与最右边我们想要得到的效果相对比,还是差了很远,出现了严重的锯齿(走样)问题。我们接下来要解决的问题就是反锯齿(走样)Aliasing。
1.1 采样基本表达
光栅化:二维点位置采样
图像:到达感光元件平面的采样
视频:对时间采样
Sampling Artifacts (Errors / Mistakes / Inaccuracies) in Computer Graphics ,举例:
摩尔纹:
时间采样种的车轮效应。
出现上述三种情况的主要原因是信号变化太快而采样过慢。
1.2 反走样技术
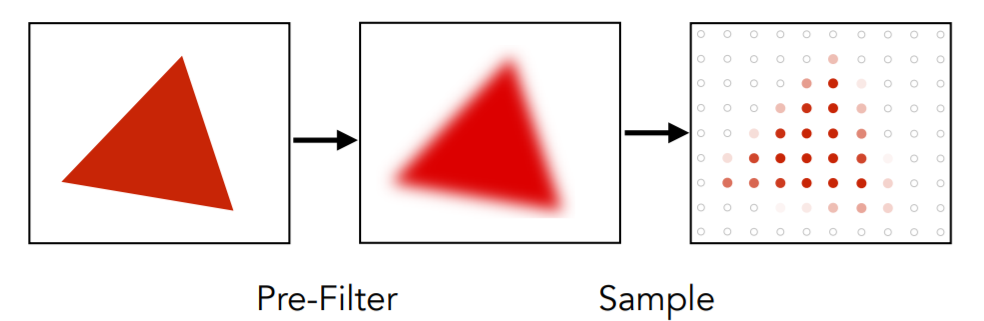
要解决上述问题,就需要用到反走样技术,在这里先给出操作的方法:先模糊(滤波)后采样
Blurring (Pre-Filtering) Before Sampling
先采样再滤波->效果很差
先滤波再采样->效果很好
2. Frequency Domain (频域)
2.1 Fourier Transform
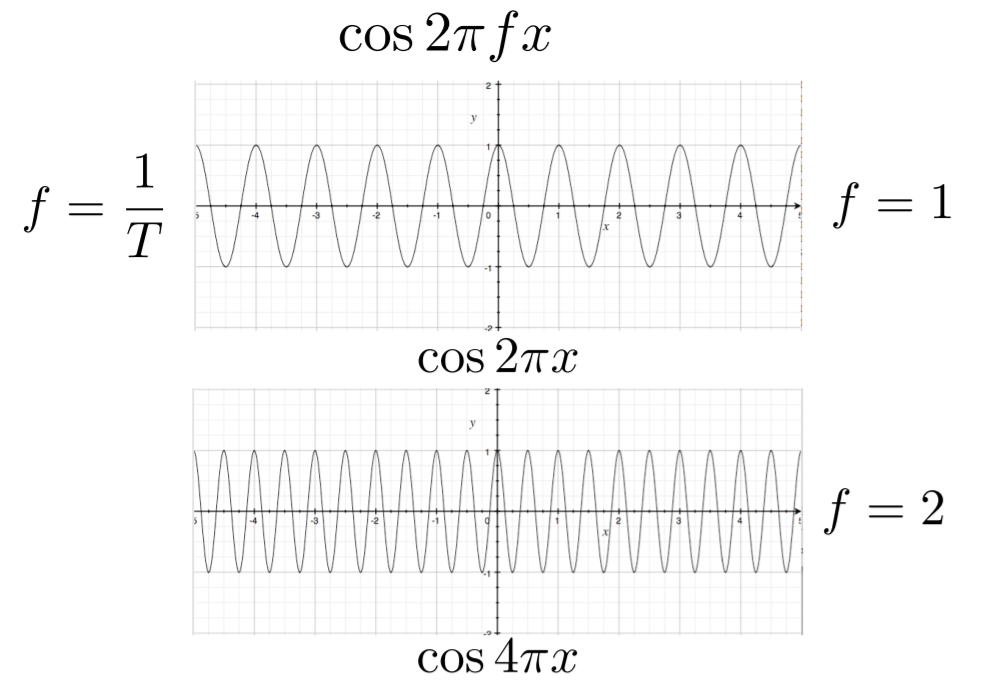
通过这张图我们可以看到,影响这个余弦波变化快慢的因素是f,即为频率,2Πfx->f=1,周期是频率的倒数。
2.2 傅里叶级数展开
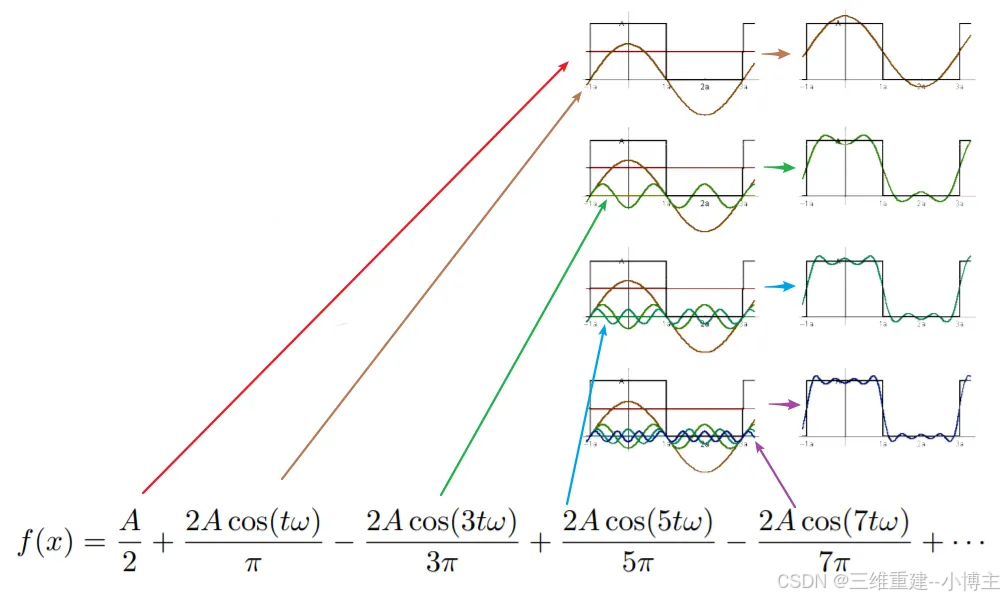
傅里叶级数展开:任何一个周期函数都可以写成一系列正弦和余弦函数的线性组合以及一个常数项
上图描述了一个像城墙一样(一个个凸起的矩形)的函数被一系列正余弦函数和一个常数项表示的过程。
从f(x)=A/2(最低的频率)开始,每次不断地向式子中加入一些正余弦函数(函数的频率不断增高),然后画出新的图像,会发现当加入的项越多时,整个f(x)函数的图像越接近于原始的那个像城墙一样(一个个凸起的矩形)的函数。
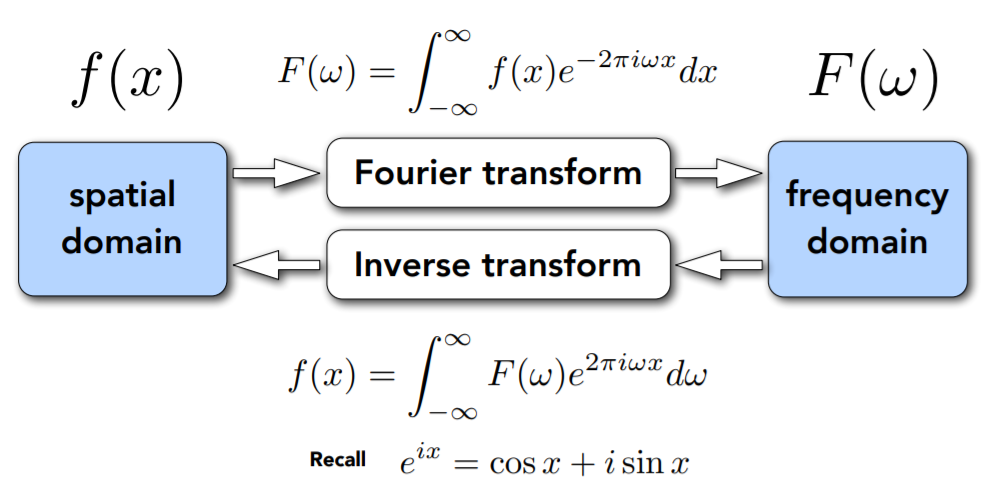
傅里叶变换:给定任何一个函数,都可以通过一系列复杂的函数变换变成另一个函数,变换后的函数还可以通过一系列操作变回原函数。这个操作就叫傅里叶变换和逆傅里叶变换。(与傅里叶级数展开相似,但本质不同,不要混淆)
所谓傅里叶变换实际就是把函数变成不同频率的段,并且我们把这些不同频率的段给显示出来。(从刚刚傅里叶级数展开的图中,我们也可以看出分解开的函数频率是不断增高的)
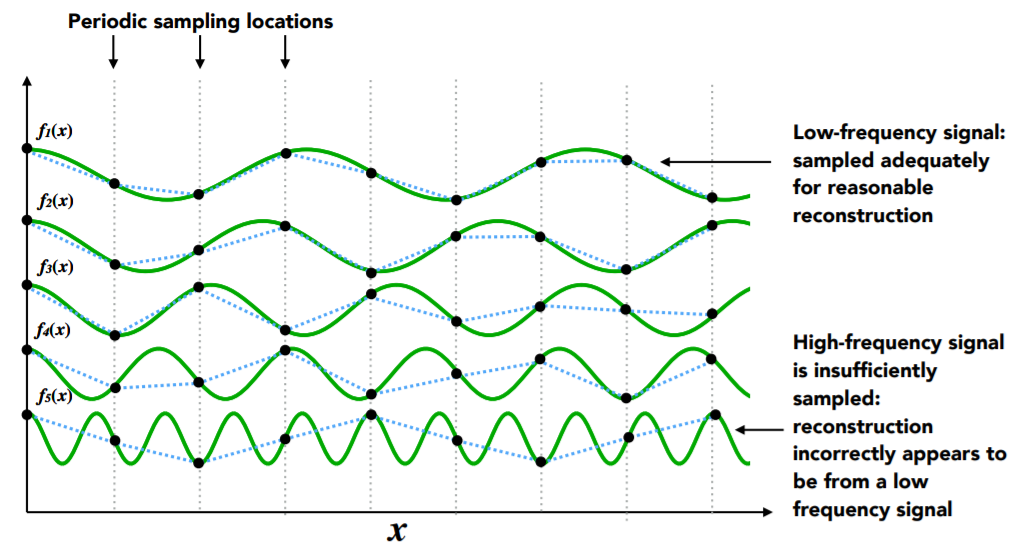
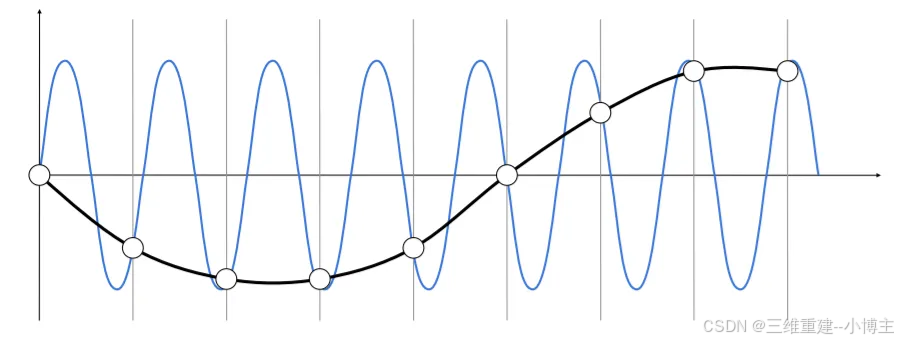
我们把一个函数分解成不同频率的函数,从上到下频率由低到高,我们用相同的采样方法(间隔相同的时间段)对这些函数进行采样。将采样后的点连起来。我们会发现,低频的函数采样后通过采样点相连依然可以大致还原出原来的函数样子,而当频率逐渐变高时,采样点相连就慢慢无法看出原来函数的样子。(说明采样和函数的频率关系很大)
通过这个例子我们可以看出,当函数频率很低的时候,我们用低频的采样就可以大致得出原来的函数,而当函数频率变高时,如果再用低频的采样,那么采样频率跟不上函数的变化,就无法恢复出原始的函数。因此我们必须用相对高的采样频率,才能还原出原来的函数。
通过频率分析走样:
假如此处我们对蓝色的函数采样,恢复出来会得到一条黑色的线。
但是假如有两个函数,一个是蓝色的函数,另一个就是这个黑色的函数,那么通过这样一个频率的采样方法,会得到一个结果:用同样的一个采样方法采样两种频率截然不同的信号,但是采样的结果却是完全相同的!
这种现象就称作走样。
3.Filtering(Filtering = Getting rid of certain frequency contents)-滤波
滤波实际就是去掉一系列的频率。
傅里叶变换实际就是把时域变换到频域。
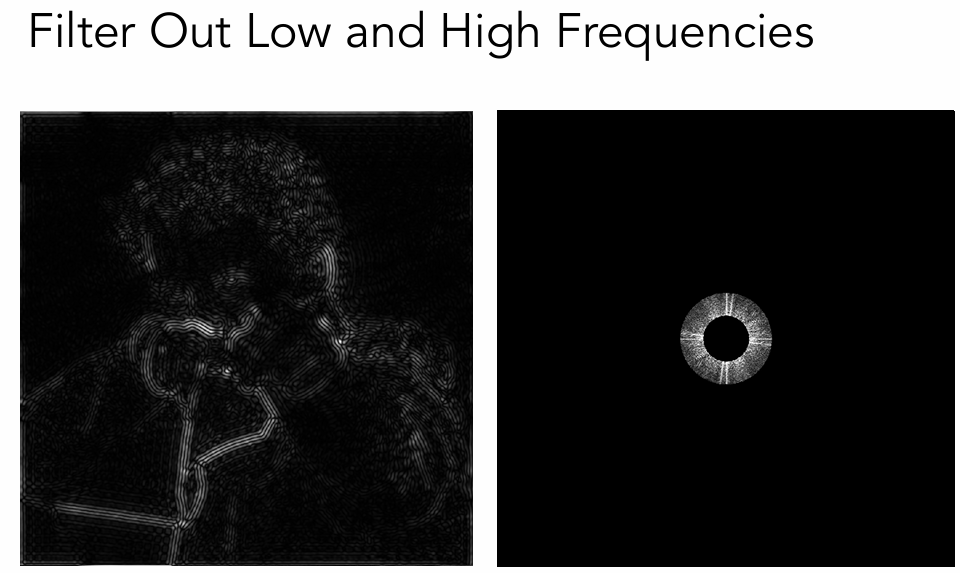
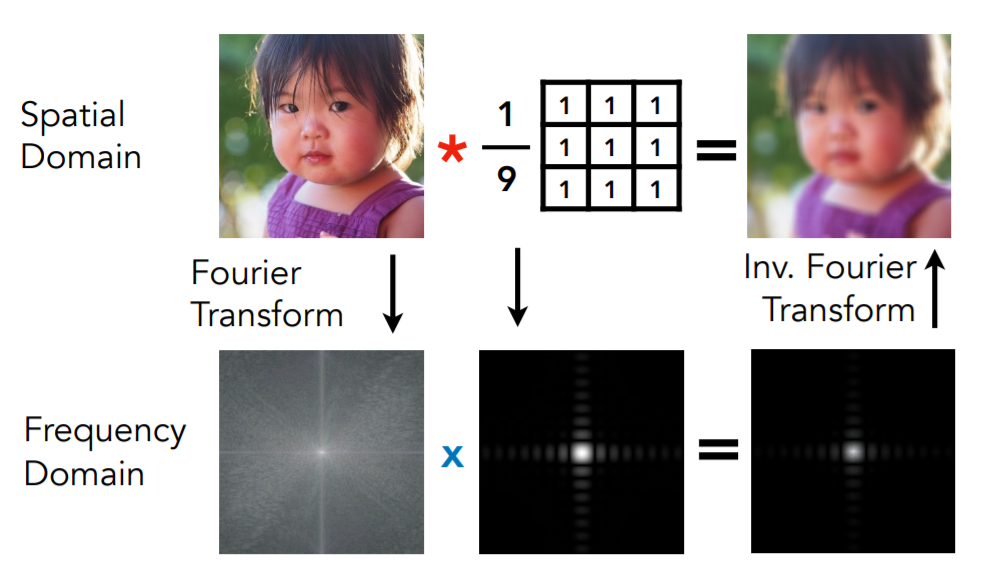
左侧的图片,通过离散傅里叶变换,得到了右边这张图。那么这张图如何去分析?
我们定义,中间为低频区域,四周为高频区域(这里的低频和高频指的是灰度图中相邻像素(假设黑是0白是1)的差,差越大频率越高)
把低频信息滤除,高频表示的图像内容的边界。—>高通滤波
我们如果去掉刚刚那副图的低频区域,那么高频区域就是图像的边缘(可以想想原因:我们平时在判断物体的边缘时,就是看颜色的突变)
而如果去掉刚刚那副图的高频区域 ,逆变换回去,那么留下的低频区域就是模糊的图像。
滤除高低的部分信息。
4. Filtering = Convolution (= Averaging) 滤波=卷积和平均
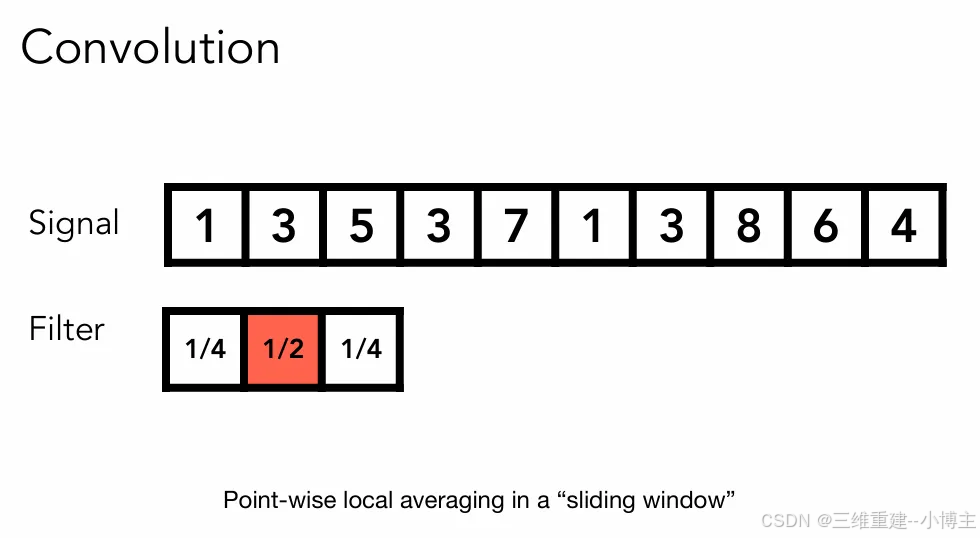
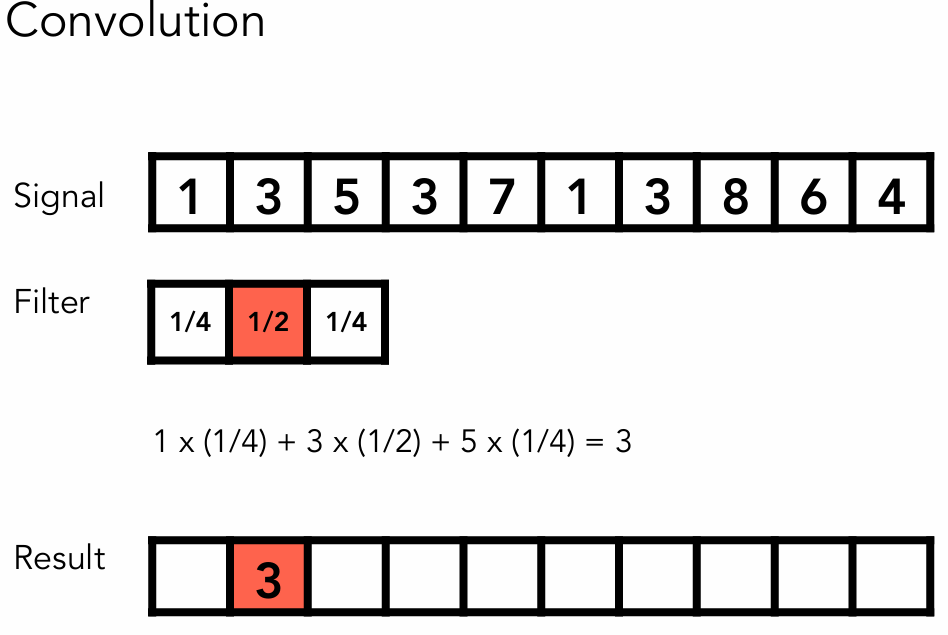
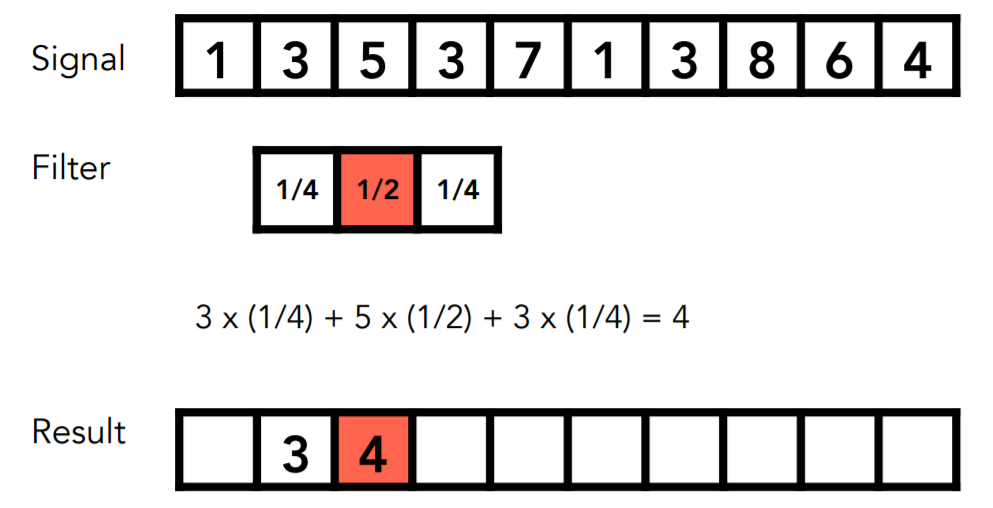
通过这个例子来理解卷积的概念:假设有一个滤波器Filter,每次用他中间的位置对应要处理的像素,周围的方块也会分别对应一个像素,用滤波器(卷积盒)和对应的像素作点乘(用相应的比例去乘以对应的像素值),得到的结果写回中间位置,即为卷积。
在这里这个例子中我们可以看到,用一个3×3的卷积盒,任何一个像素都是他周围对应的9个格子的像素的平均,那结果也就是一个模糊的图像。图像和卷积盒都可以通过傅里叶变换在频域上表示出来,时域上做的卷积就相当于在频域上的信号相乘。最终得到的频域变换通过傅里叶逆变化得到卷积变换后的图像。
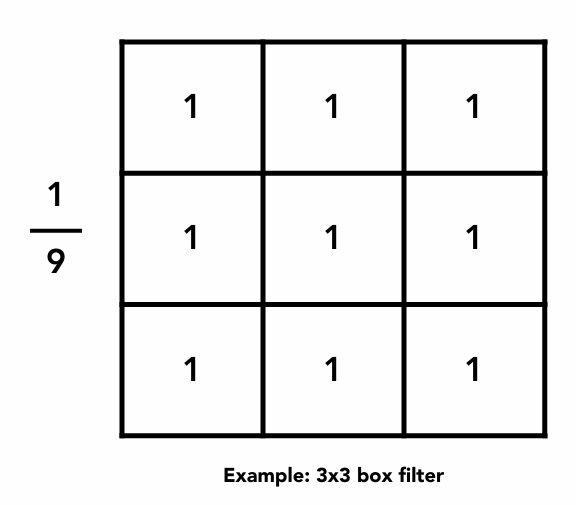
4.1 Box Filter (相当于卷积核)
卷积核变小->频域上变大
卷积核变大->频域上变小
理由如下:用一个小的卷积盒(假设3×3),模糊的程度可能不是很大,但是要用一个很大的卷积盒(假设63×63)去对这个图像进行卷积操作,得到的图像肯定会越来越模糊,那么也就只能留下更低的频率。
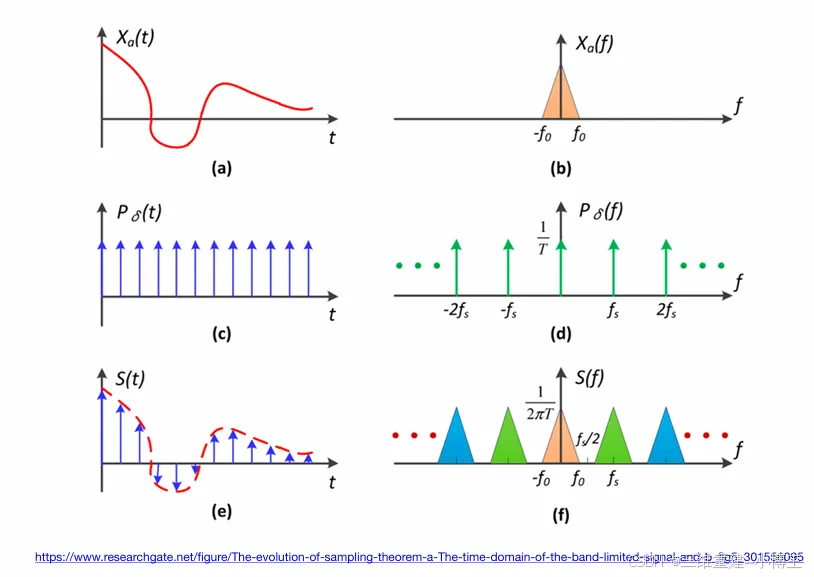
5. Sampling = Repeating Frequency Contents (采样就是在重复频率上的内容)
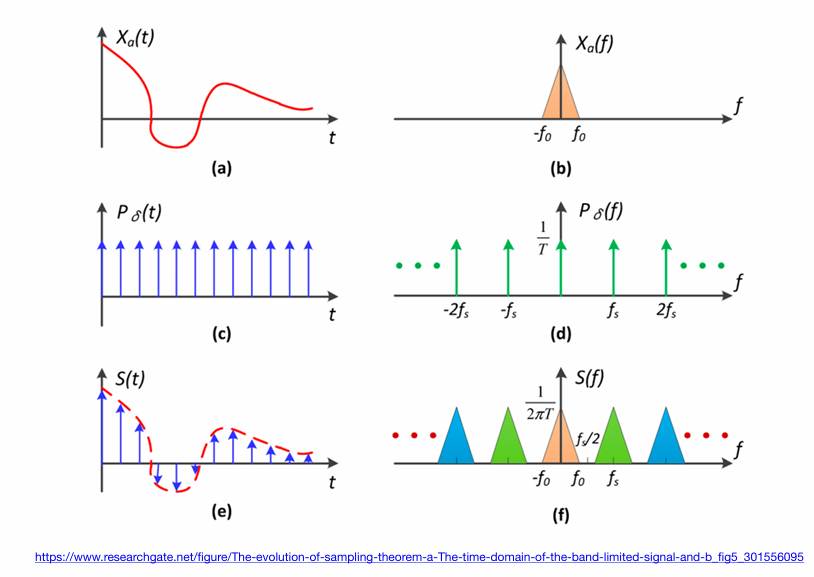
(a)是某个连续的函数,假设他通过傅里叶变换反应在某个频域上是(b),假如要采样这个函数,就要在这个函数上乘以另外一个只在固定位置上有值的函数(冲激函数,如(c)),用(a)乘以(c),得到的就是(a)函数上的一系列连续的点(e)
由于时域上的乘积等于频域上的卷积,所以(f)就是(b)卷积(d)的结果。我们可以发现(f)不过是(b)复制粘贴的重复过程。
5.1 Aliasing = Mixed Frequency Contents
如果采样率合适,如图上方的图,则没有什么问题,如果采样率不足(采样不够快),那么信号“复制粘贴”中间的间隔就会非常小(采样间隔时间大,换算成频率的话就是频率间隔小(两者是倒数关系)),所以原始信号和“复制粘贴”的信号就会出现叠加,这种情况就叫发生了走样。所谓走样在频率的角度上来讲就是频率的频谱在经过“复制粘贴”的情况下发生了混合(混叠)。
5.2 思考如何消除走样
How Can We Reduce Aliasing Error?
Option 1: Increase sampling rate(增加采样率)
• Essentially increasing the distance between replicas in the Fourier domain
• Higher resolution displays, sensors, framebuffers…
• But: costly & may need very high resolution
Option 2: Antialiasing
• Making Fourier contents “narrower” before repeating
• i.e. Filtering out high frequencies before sampling
Antialiasing = Limiting, then repeating
先模糊,后采样。先通过一个低通滤波,把信号的高频的信息拿掉,然后再采样。如图,我们就会发现,信号对应的频谱就不会发生混叠了。
5.3 Antialiased Sampling
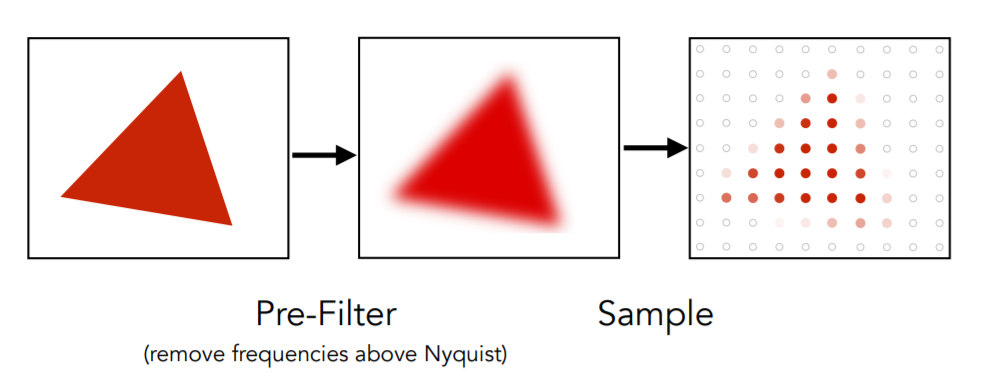
回到这节课一开始的问题,我们如何将这个三角形变模糊,答案也就很明确了。
用一个合适的低通滤波器。
Antialiasing by Computing Average Pixel Value
Solution:
Convolve f(x,y) by a 1-pixel box-blur
--Recall: convolving = filtering = averaging
Then sample at every pixel’s center
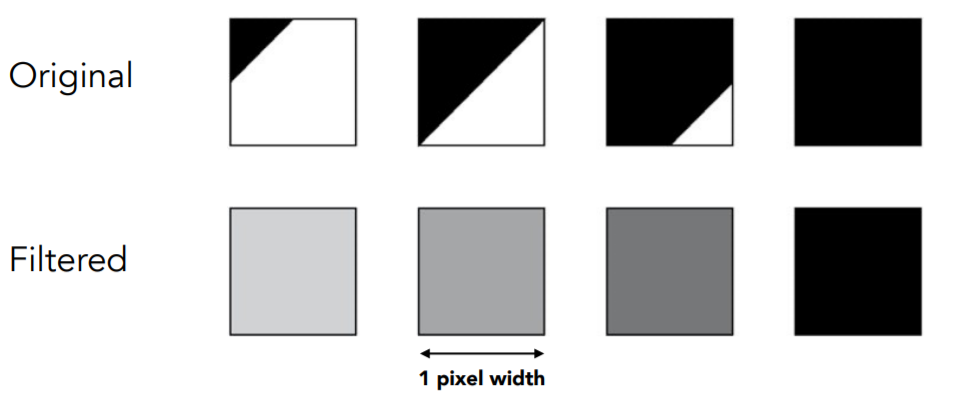
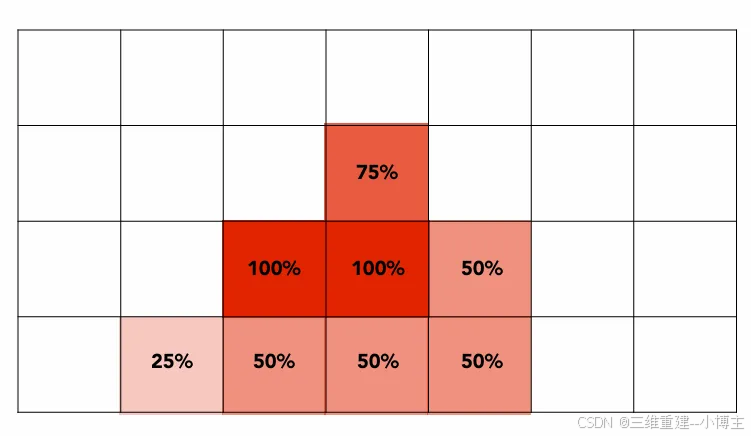
In rasterizing one triangle, the average value inside a pixel area of f(x,y) = inside(triangle,x,y) is equal to the area of the pixel covered by the triangle
如图,假设最左边的黑色覆盖了1/8,即有7/8没覆盖,也就是有87.5%的白色,最右边的黑色全部覆盖,也就是有0%的白色(纯黑色)。
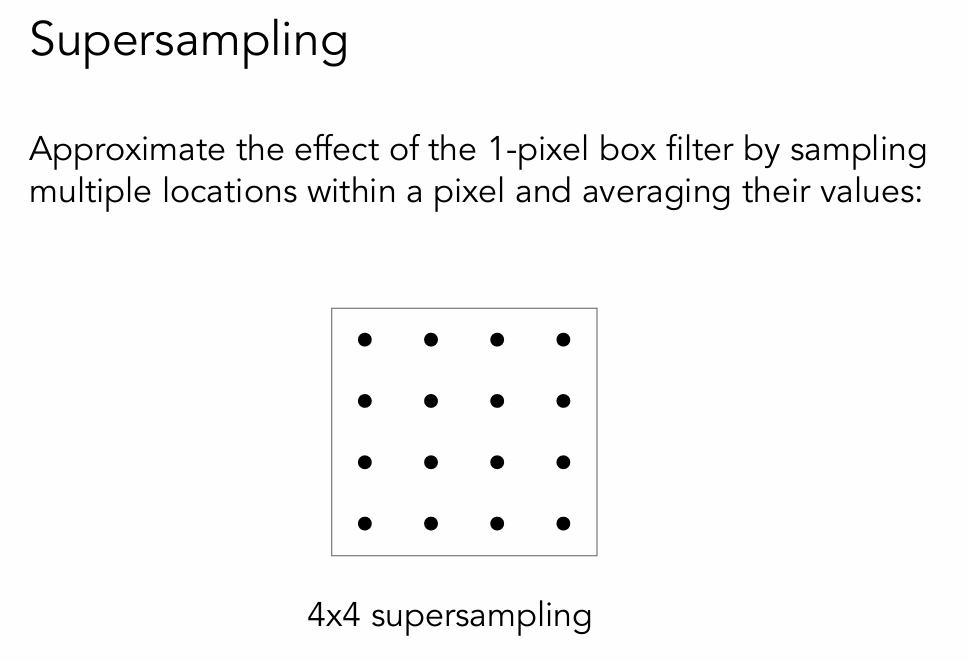
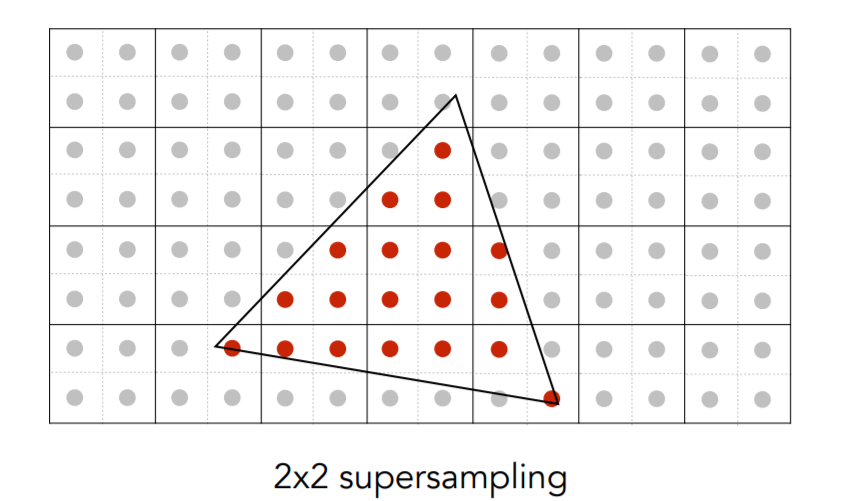
6.Antialiasing By Supersampling (MSAA)->反走样的近似,并不能严格意义上解决反走样
对于任何一个像素里面,我再把这个像素划分成好多小的像素,每个小的像素也有各自的中心,再利用同样的方法去操作。
Supersampling: Step 1
Take NxN samples in each pixel.
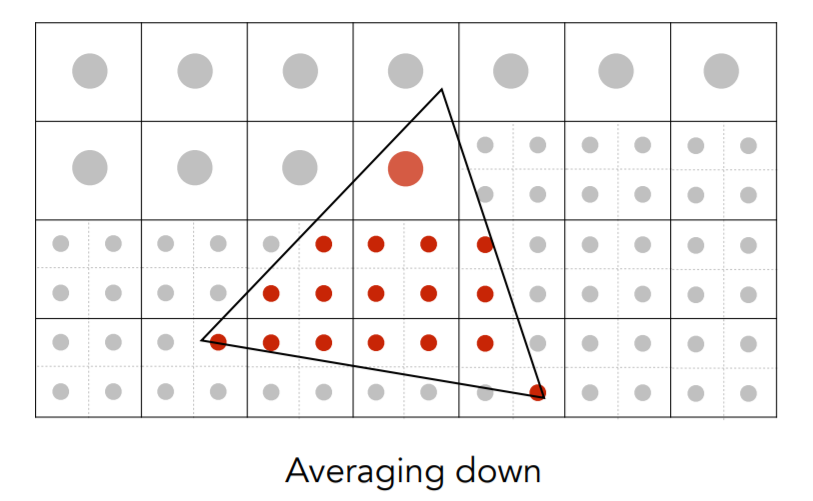
Supersampling: Step 2
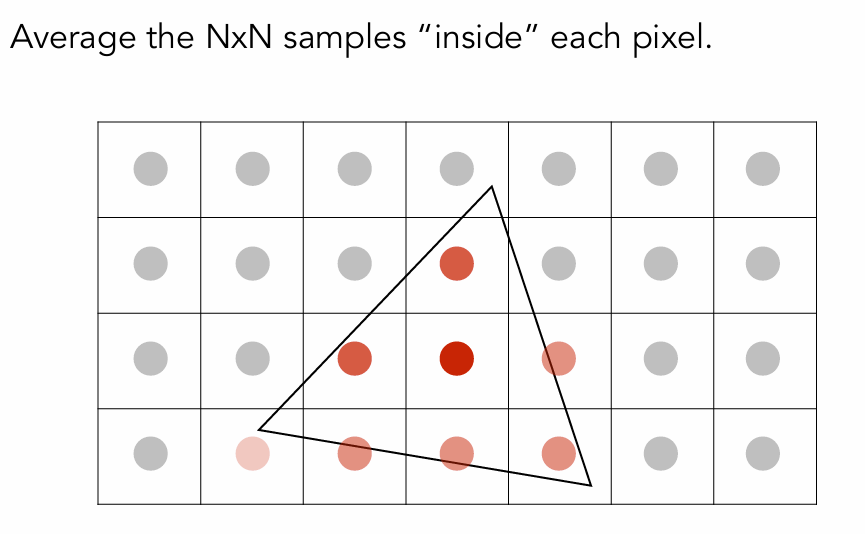
Average the NxN samples “inside” each pixel.
Supersampling: Result
This is the corresponding signal emitted by the display
No free lunch!
What’s the cost of MSAA?
为了引入MSAA,代价是增大了计算量,但是不是成指数倍增加的,在工业界中,人们并不是规则的划分网格,而是用一些更加有效的图案,甚至有一些点还会被临近的像素所复用。因此如果打游戏启用抗锯齿,假设用4倍,帧率并不会掉到原来的1/4,就是这个原因。
Milestones
FXAA (Fast Approximate AA->快速近似抗锯齿) (图像的后期处理,先得出有锯齿的图,再去用图像处理的方式,把边界找到,并且把这些边界换成没有锯齿的边界)
TAA (Temporal AA) (找上一帧的信息,复用上一帧的像素值)
Super resolution / super sampling (超采样->超分辨率)(和抗锯齿不太一样,但都是解决样本不足的问题。把一张小图拉大,但又不想看到锯齿或者说有一张高分辨率图,但是采样率不够,想把高分辨率的图恢复出来)
From low resolution to high resolution
Essentially still “not enough samples” problem
DLSS (Deep Learning Super Sampling) (深度学习=猜!)
一切适合“猜”的技术->深度学习
二、 Visibility / occlusion (可见性/遮挡)— Z-buffering (深度缓存)
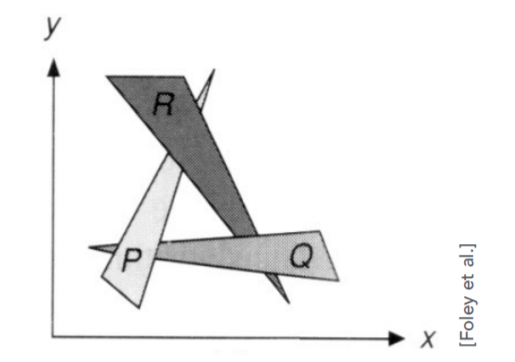
但是会出现一个问题:一旦有三个三角形,互相覆盖互相部分遮挡(如上图R、P、Q),那么就无法判断谁在前谁在后。因此我们引入了Z-buffer(深度缓存)的概念
Z-buffer
Store current min. z-value for each sample (pixel)
Needs an additional buffer for depth values
–frame buffer stores color values**(储存颜色)**
–depth buffer (z-buffer) stores depth**(储存深度)**
IMPORTANT: For simplicity we suppose z is always positive (smaller z -> closer, larger z -> further)—>越近值越小,越远值越大
对每一个像素来看,永远去记录像素表示的几何离我们的最浅(最靠前,最近)深度。
在渲染生成图像(上方左侧图)的同时,也会生成另一张图像,这张图只存任何一个像素所看到的几何物体最浅的深度信息,叫做深度缓存图(上方右侧图),利用这张图去维护遮挡关系的信息。
特别注意的是,这张Depth/Z-buffer图中,颜色的灰度代表点距离摄像机的远近,黑色代表近,白色代表远。
假设左边这幅图一开始渲染地板,右边的Depth/Z-buffer图中先将各个像素点的地板深度信息存储进去,后来在渲染左边的立方体的时候,一些像素点的地板被立方体遮挡,这时候右边更新深度信息,将那些遮挡地板的立方体所在的各个像素点的的深度信息储存进去。
for (each triangle T)
for (each sample (x,y,z) in T)
if (z < zbuffer[x,y]) // closest sample so far
{framebuffer[x,y] = rgb; // update color
zbuffer[x,y] = z;} // update depth
else
; // do nothing, this sample is occluded
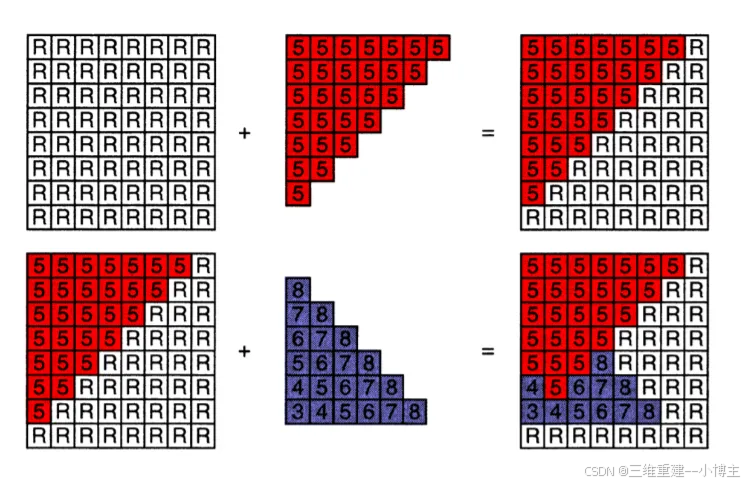
如图,一开始认为所有像素的深度无限大,后来加上了红色三角形,其深度都为5,这些像素深度原来是R(无限大),因此新加进来的像素深度5比一开始的小,于是将其替换。后来加上了蓝色三角形,将这些区域的像素深度与刚刚同位置的像素深度比较,小的替换掉大的(即近的遮挡住远的)。
深度缓存复杂性:
O(n) for n triangles (assuming constant coverage)
How is it possible to sort n triangles in linear time?
–在此处我们要知道,我们并没有提前排序,对于任意一个像素只是记录当前看到的最小值。
Most important visibility algorithm
Implemented in hardware for all GPUs
处理不了透明物体。
参考信息
1、Lecture 06 Rasterization 2 (Antialiasing and Z-Buffering)_哔哩哔哩_bilibili
2、GAMES101: 现代计算机图形学入门 (ucsb.edu)
3、https://blog.csdn.net/weixin_44848751/article/details/127881504