本文涉及知识点

割点 图论知识汇总
C++BFS算法

LeetCode2556. 二进制矩阵中翻转最多一次使路径不连通

给你一个下标从 0 开始的 m x n 二进制 矩阵 grid 。你可以从一个格子 (row, col) 移动到格子 (row + 1, col) 或者 (row, col + 1) ，前提是前往的格子值为 1 。如果从 (0, 0) 到 (m - 1, n - 1) 没有任何路径，我们称该矩阵是 不连通 的。
你可以翻转 最多一个 格子的值（也可以不翻转）。你 不能翻转 格子 (0, 0) 和 (m - 1, n - 1) 。
如果可以使矩阵不连通，请你返回 true ，否则返回 false 。
注意 ，翻转一个格子的值，可以使它的值从 0 变 1 ，或从 1 变 0 。
示例 1：

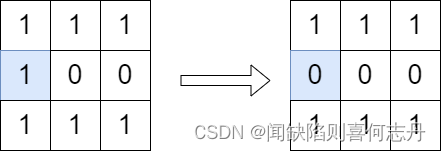
输入：grid = [[1,1,1],[1,0,0],[1,1,1]]
输出：true
解释：按照上图所示我们翻转蓝色格子里的值，翻转后从 (0, 0) 到 (2, 2) 没有路径。
示例 2：

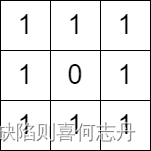
输入：grid = [[1,1,1],[1,0,1],[1,1,1]]
输出：false
解释：无法翻转至多一个格子，使 (0, 0) 到 (2, 2) 没有路径。
m == grid.length
n == grid[i].length
1 <= m, n <= 1000
1 <= m * n <= 10⁵
grid[0][0] == grid[m - 1][n - 1] == 1

割点

如果有封装类，直接使用割点更简单。

BFS

vector<unorder_set>> leve[i] 记录i步可以到达的坐标,i$\in$[0,m-1+n-1]
如果leve.size()小于等于2，只经过起点和终点，所以一定能够连通。
否则 返回 cout(leve.begin()+1,leve.end()-1,1) > 0 。
由于只能向右或下走，所以不会有环。只需要处理，同一步的重复。

错误

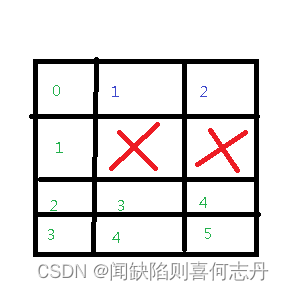
必须排除无法到达终点的点。如：

图中的数字表示多少步到达此格。绿色数字表示能到达终点，蓝色数字表示无法到达终点。叉叉表示grid[r][c]为0而无法进入。
canVis记录各点能否到达终点，不能到达终点的点忽略。

代码

核心代码

class Solution {
public:
	bool isPossibleToCutPath(vector<vector<int>>& grid) {
		const int R = grid.size();
		const int C = grid[0].size();
		vector<vector<bool>> canVis(R, vector<bool>(C));
		canVis.back().back() = true;
		for (int r = R - 1; r >= 0; r--) {
			for (int c = C - 1; c >= 0; c--) {
				if ((r + 1 < R) && canVis[r + 1][c]&& grid[r + 1][c]) {
					canVis[r][c] = true ;
				}
				if ((c + 1 < C) && canVis[r][c + 1]&& grid[r][c + 1]) {
					canVis[r][c] = true;
				}
			}
		}

		const int m = R - 1 + C - 1;
		vector<set<pair<int, int>>> leves(m + 1);
		leves[0].emplace(0, 0);
		for (int i = 0; i < m; i++) {
			for (auto [r, c] : leves[i]) {
				if ((r + 1 < R) && grid[r + 1][c] && canVis[r + 1][c]) {
					leves[i + 1].emplace(r + 1, c);
				}
				if ((c + 1 < C) && grid[r][c + 1] && canVis[r][c + 1]) {
					leves[i + 1].emplace(r , c + 1);
				}
			}
		}
		if (leves.back().empty()) { return true; }
		for (int i = 1; i < m; i++) {
			if (1 == leves[i].size()) { return true; }
		}
		return false;
	}
};

单元测试

template<class T1, class T2>
void AssertEx(const T1& t1, const T2& t2)
{
	Assert::AreEqual(t1, t2);
}
void AssertEx( double t1,  double t2)
{
	auto str = std::to_wstring(t1) + std::wstring(1,32) + std::to_wstring(t2);
	Assert::IsTrue(abs(t1 - t2) < 1e-5,str.c_str() );
}

template<class T>
void AssertEx(const vector<T>& v1, const vector<T>& v2)
{
	Assert::AreEqual(v1.size(), v2.size());
	for (int i = 0; i < v1.size(); i++)
	{
		Assert::AreEqual(v1[i], v2[i]);
	}
}

template<class T>
void AssertV2(vector<vector<T>> vv1, vector<vector<T>> vv2)
{
	sort(vv1.begin(), vv1.end());
	sort(vv2.begin(), vv2.end());
	Assert::AreEqual(vv1.size(), vv2.size());
	for (int i = 0; i < vv1.size(); i++)
	{
		AssertEx(vv1[i], vv2[i]);
	}
}

namespace UnitTest
{
	vector<vector<int>> grid;
	TEST_CLASS(UnitTest)
	{
	public:
		TEST_METHOD(TestMethod00)
		{
			grid = { {1,1,1},{1,0,0},{1,1,1} };
			auto res = Solution().isPossibleToCutPath(grid);
			AssertEx(true, res);
		}
		TEST_METHOD(TestMethod01)
		{
			grid = { {1,1,1},{1,0,1},{1,1,1} };
			auto res = Solution().isPossibleToCutPath(grid);
			AssertEx(false, res);
		}
		TEST_METHOD(TestMethod02)
		{
			grid = { {1,1,1},{1,0,0},{1,1,1},{1,1,1} };
			auto res = Solution().isPossibleToCutPath(grid);
			AssertEx(true, res);
		}
	};
}