KMP算法简介

KMP算法，全称为Knuth-Morris-Pratt算法，是一种高效的字符串匹配算法。它通过预处理模式串（子串），构建一个部分匹配表（也称为next数组），使得在文本 （主串）中匹配时，当遇到不匹配的情况，能够利用已匹配的部分信息，将模式串合理地向后滑动，避免从头开始匹配，从而提高匹配效率。

KMP算法的核心思想

• 一般的暴力求解很简单，很容易理解，但是在时间复杂度上远远不如KMP算法。
暴力求解在配对时只要遇到不相同的字符，则跳回序列第一个元素重新匹配，如果运气不好的话，其中所需要时间之大可想而知。

• 但是，KMP算法很好的解决了这个问题，它利用next数组使得代码呈线性时间复杂度，大大减少了时间上的浪费，可以说它最核心的内容就在于用next数组选择合适起点进行匹配，使循环一直向前，不会返回重复匹配。

KMP算法分解

• 进行字符匹配
先说字符匹配，这可以让我们理解next存在的意义。
代码如下：

int KMP(char major[], char match[], int next[],int match_lengh)
{
    int i = 0;
    int j = 0;
    
    while(j<match_lengh)
    {
        if(match[j]==major[i])//当前元素配对成功后，开始配对下一个元素
        {
            i++;
            j++;
        }
        else
            if(j==0)//配对失败后若前一位元素的next数值为零，则直接跳过该major元素
                i++;
            else
                j = next[j-1];//匹配失败后根据前一位元素的next数值判断可以跳过几个字符
    }
    if(j==match_lengh)
        return i - j;
    else
        return -1;
}

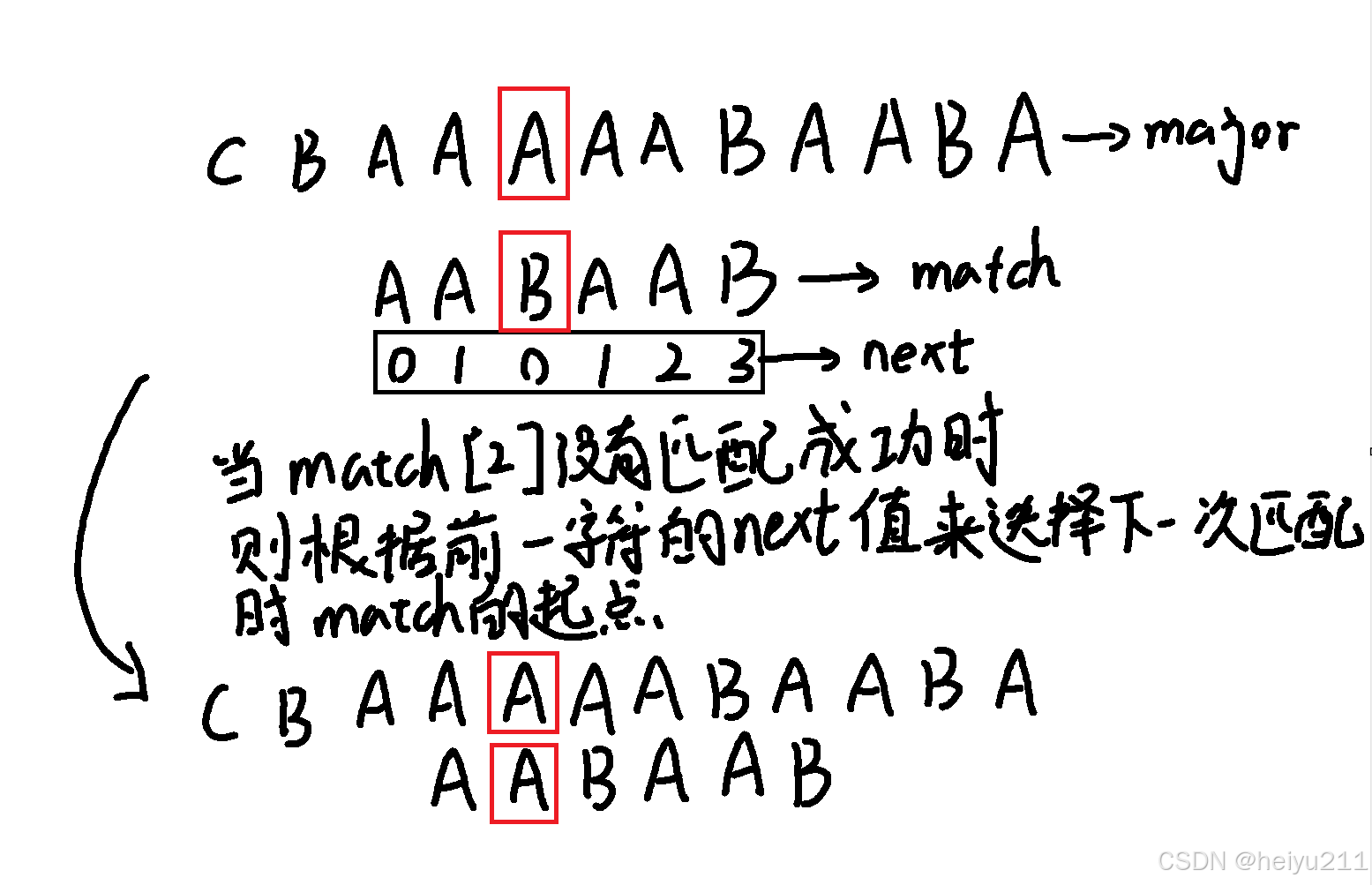
• 对于上面代码，我再用画图的方式举个例子：

注：这里的major和match只是代号（数组名），下次match的起点即match[next值]
而major所被配对的元素不变。

可是为什么是这样的工作原理呢，那我们得先知道next数组是什么
• • next数组
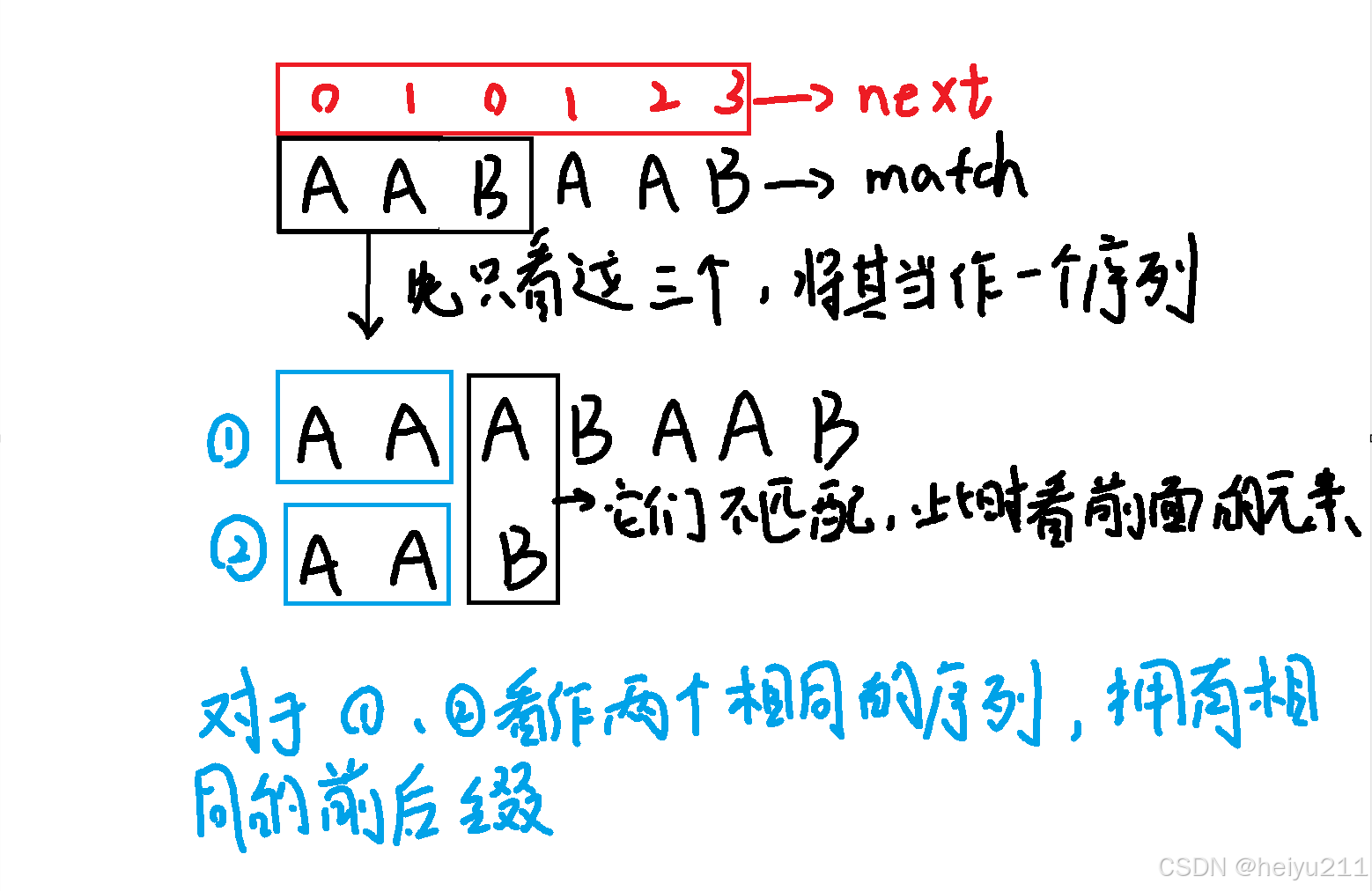
next数组（next中元素与match中元素是一一对应的）记录的其实是一串序列的相同前后缀的长度，举个例子：
对于“AA”，它有相同的前后缀A且长度为1，对于“AABBAA”它的相同前后缀为“AA”
长度为2.

根据以上内容我们可以知道next的第一层含义：
若next[i]=a，则match[0]~match[i]的序列有相同的前后缀且长度为a

这里我再作图解释一下：
图1：

图2：

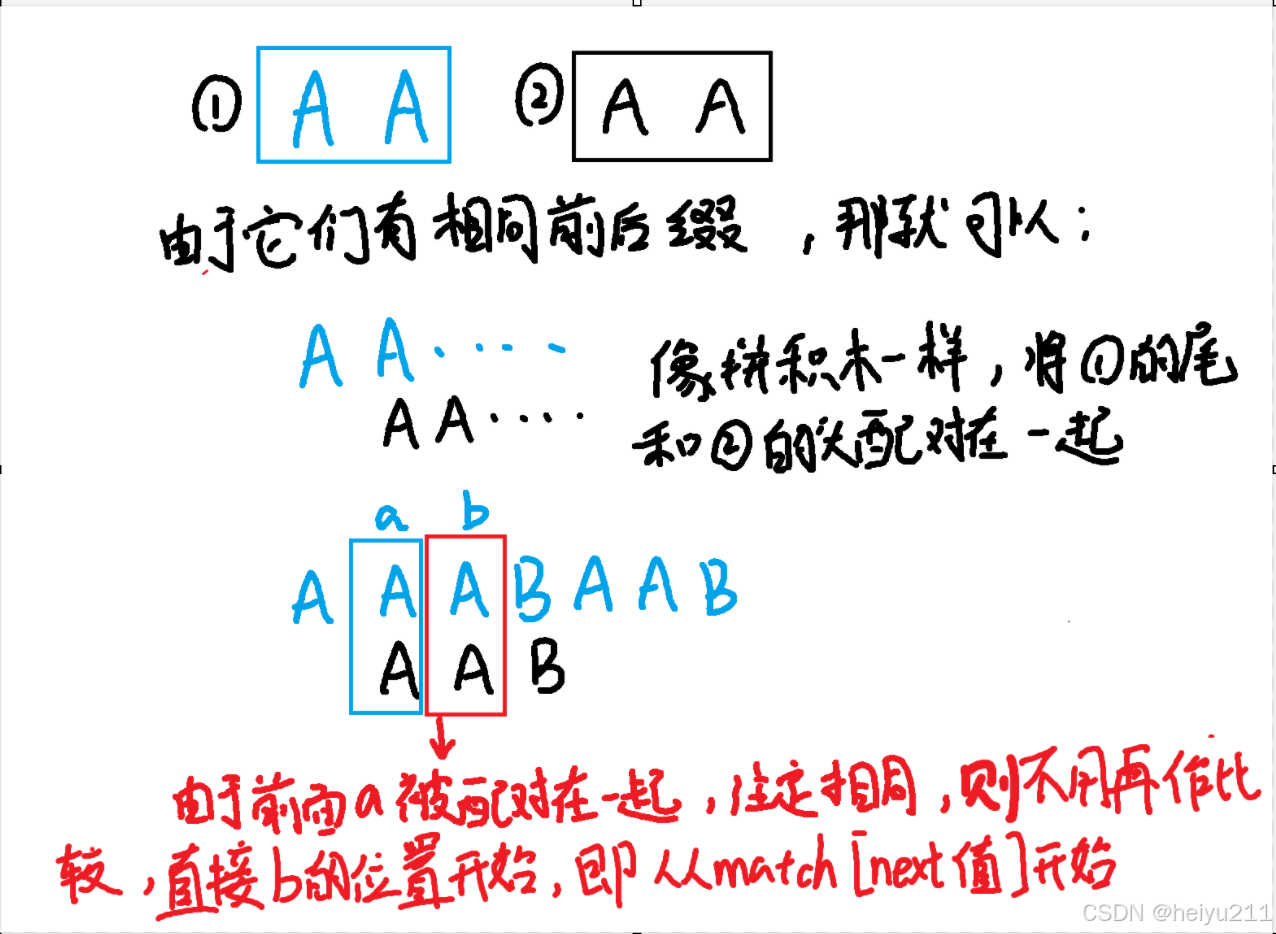
到这里我们又可以知道next数组的第二层含义：
即next[i]=a时，下一次匹配从match[a]开始(major中所被配对的元素不变)

那我们这里再举个例子：

其实还有一种特殊情况，即next值等于0时，如果是next[0]=0，则major所被配对的元素向后移一位( 当然，起点也要改变 )，如果是next[i]=0(i != 0)，则下一次匹配以match[0]为起点(想象一下，对于没有相同前后缀的序列，若下一个元素也不匹配，那么在major中的这段序列则一定不属于我们要找到的那段序列之中，所以可以直接跳过，以match[0]为起点)

• 创建next数组
• • 代码如下：

void build_next(int next[],int sz_next,char match[])
{
    int i = 1;//直接跳过i=0，因为第一个元素与它自己比较没有意义
    int affix_lengh = 0;//前后缀的长度
    while(i<sz_next)
    {
        if(match[i]==match[affix_lengh])
        {
            affix_lengh++;//如果相同前后缀长度加一
            next[i] = affix_lengh;//并把该长度赋当前next元素
            i++;//当前元素比较完后，切换到下一个元素
        }
        else
        {
            if (next[affix_lengh] == 0)//如果affix_lengh为0了都没有找到相同元素，就直接跳过
                i++;
            else
            {
                affix_lengh = next[affix_lengh - 1];//不相同后再切换前一个元素进行比较
            }
        }
    }
    return;
}

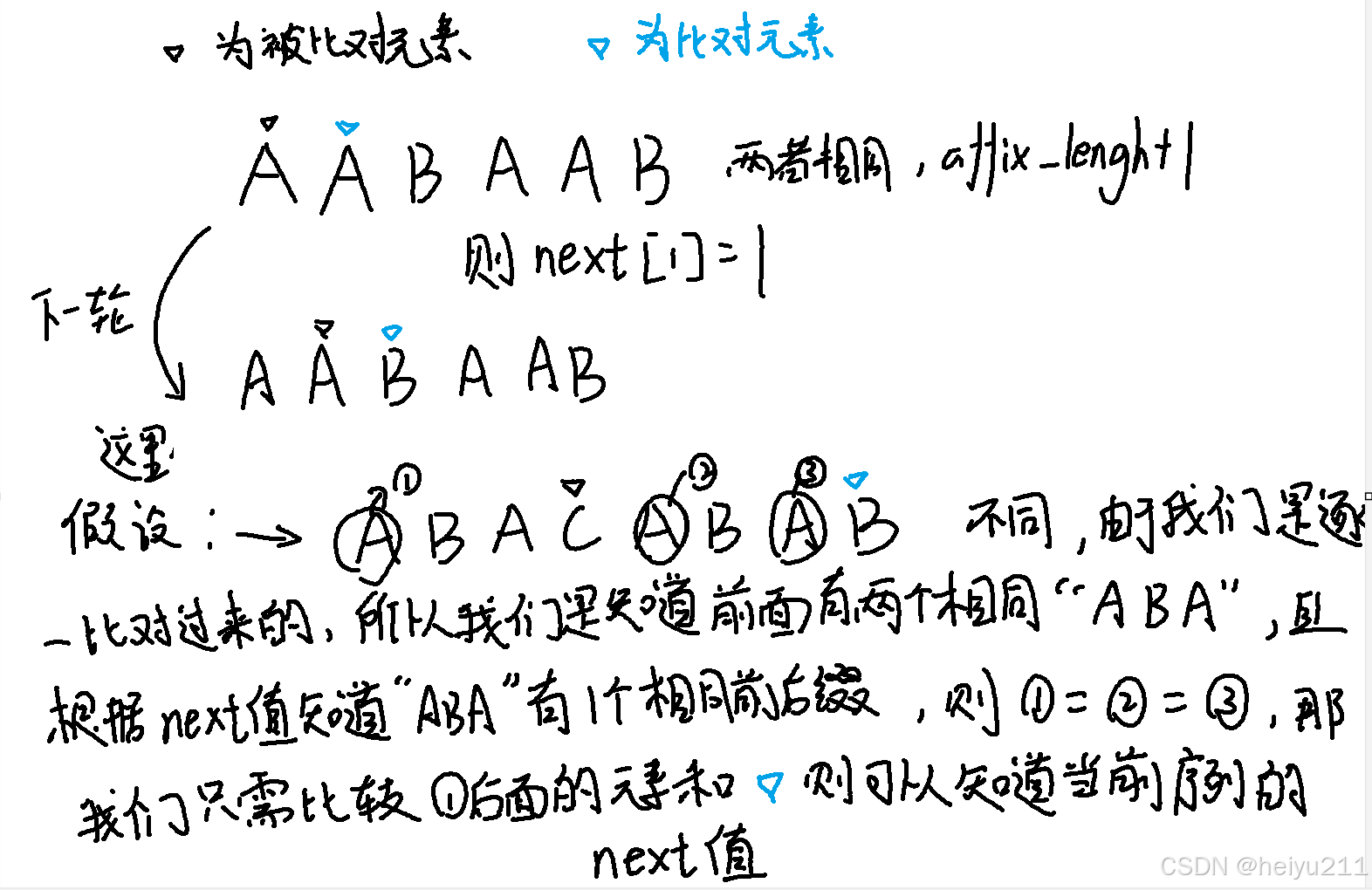
• • affix_lengh的作用：
1.affix_lengh记录了被比对元素的位置
2.记录了当前序列相同前后缀长度（若比对元素的位置为match[i],且affix_lengh=1，则match[0]~match[i]的序列有1个相同前后缀）

这里直接上图吧：

完整代码：

#include <stdio.h>
#include <string.h>

int KMP(char major[], char match[], int next[],int match_lengh);

void build_next(int next[],int sz_next,char match[]);

int main()
{
    char major[50] = "ABCBAABAABBA";
    char match[] = "AABAAB";
    int next[6] = {0};
    int match_lengh = strlen(match);//需要匹配的序列的元素个数

    build_next(next, match_lengh, match);//建立match的next数组

    int first;
    first = KMP(major, match, next,match_lengh);//指成功配对后match中第一个元素在major中的位置

    if(first==-1)//匹配失败的情况
    {
        puts("matchingg failed");
    }
    else//匹配成功
    {
        puts("match successful");
        printf("it is between major[%d] and major[%d]", first, first + match_lengh);
    }
    return 0;
}

int KMP(char major[], char match[], int next[],int match_lengh)
{
    int i = 0;
    int j = 0;
    
    while(j<match_lengh)
    {
        if(match[j]==major[i])//当前元素配对成功后，开始配对下一个元素
        {
            i++;
            j++;
        }
        else
            if(j==0)//配对失败后若前一位元素的next数值为零，则直接跳过该major元素
                i++;
            else
                j = next[j-1];//匹配失败后根据前一位元素的next数值判断可以跳过几个字符
    }
    if(j==match_lengh)
        return i - j;
    else
        return -1;
}

void build_next(int next[],int sz_next,char match[])
{
    int i = 1;//直接跳过i=0，因为第一个元素与它自己比较没有意义
    int affix_lengh = 0;//前后缀的长度
    while(i<sz_next)
    {
        if(match[i]==match[affix_lengh])
        {
            affix_lengh++;//如果相同前后缀长度加一
            next[i] = affix_lengh;//并把该长度赋当前next元素
            i++;//当前元素比较完后，切换到下一个元素
        }
        else
        {
            if (next[affix_lengh] == 0)//如果affix_lengh为0了都没有找到相同元素，就直接跳过
                i++;
            else
            {
                affix_lengh--;//不相同后再切换前一个元素进行比较
            }
        }
    }
    return;
}

（哇，这玩意写得真的好麻烦，我已经尽力了，如果我写的哪里有问题，评论区告诉我一下杯😀）