Bootstrap

平衡查找树(数据结构篇)

数据结构之平衡查找树

平衡查找树(AVL树)

概念：

  • 为了防止因为插入删除而导致的树结构不平衡(通常我们删除节点总是对右子树的最小值节点替代操作，而不是交替的利用左子树的最大值节点替代，这就将导致左子树的平均深度大于右子树平均深度，直接导致整颗树平均深度的增加，导致对树节点的操作时间增长)，导致对树的操作所用时间成倍数增长的问题，我们采用平衡二叉树—左右子树的平均深度差不多，达到一种平衡的操作，平衡二叉树希望对树的任意节点的操作时间为O(logN)
  • AVL(Adelson-Velskii和Landis)树是带有平衡条件的二叉查找树。这个平衡条件需要容易保持，而且需保证树的深度是O(logN)。
  • 一颗AVL树是其每个节点的左子树和右子树的高度最多差1的二叉查找树，空树的高度定义为-1
  • 在高度为h的AVL树中，最少节点数S(h)由S(h)=S(h-1)+S(h-2)+1算出。该h为该数最大高度。

旋转：

  • 功能：对被破坏平衡的AVL树进行修正，使得重新平衡

  • 对于我们对树的插入操作，破坏AVL树的平衡，我们则需要对树进行简单的修正来保持平衡，这个操作我们称其为旋转

  • 我们把必须重新平衡的节点(就是造成AVL树不平衡的插入点跟因此被打破平衡的另外一个节点(也就是插入点跟树中的一个节点高度差大于1)的共同根节点)叫做α，由于任意节点最多有两个儿子，因此高度不平衡时，α点的两颗子树的高度差2，这种不平衡的情形有四种：

    1.对α的左儿子的左子树进行一次插入

    2.对α的左儿子的右子树进行一次插入

    3.对α的右儿子的左子树进行一次插入

    4.对α的右儿子的右子树进行一次插入

  • 对于1和4的情形称为插入发生在"外边"的情况(即左-左的情况或右-右的情况)，该情况需要通过对树的一次单旋转而完成调整

  • 对于2和3的情形称为插入发生在"内部"的情况(即左-右的情况或右-左的情况)，这个情况需要通过对树的双旋转来处理

单旋转

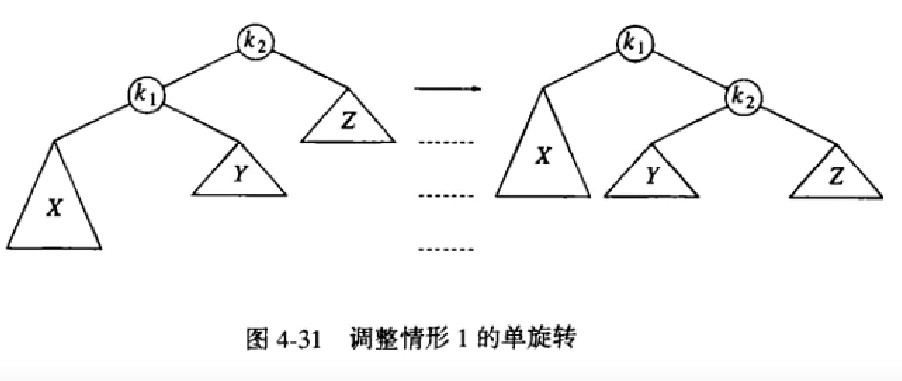
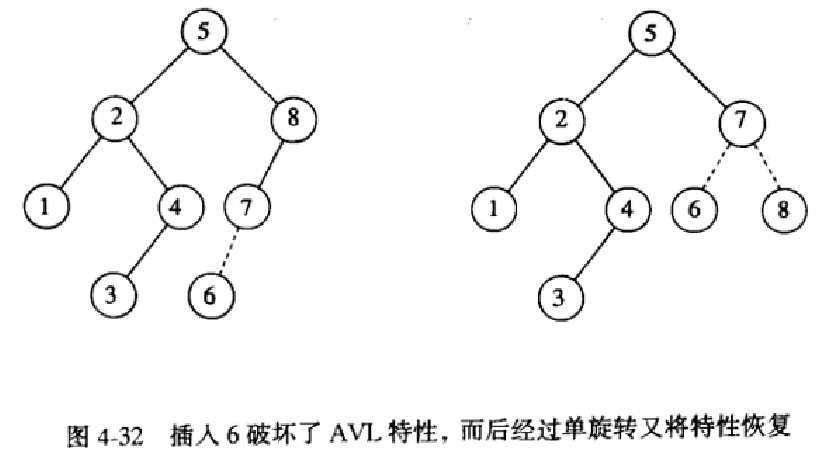
  • 对于情形1(如图4-31)，我们需要将造成不平衡的插入点上移一层，另外那个跟它高度差为2的节点下移一层(就是将α点跟其左节点进行单旋转(单旋转就是类似将左节点拎起来，其他的节点根据重量下坠，然后再根据二叉查找树的特性排序形成新的平衡二叉树))，并形成一个新的平衡二叉查找树，具体操作就如图4-32，插入6会破坏AVL树的特性，因为6是插入点，而8没有子节点(这个空的子节点其实就是被破坏平衡的高度差为2的节点)，它们的共同根节点就为8，所以8为α点，我们需要将α点的左节点也就是7跟α点也就是8进行单旋转，然后形成新的平衡查找树

    具体操作为：

    1. 向α点的左儿子的左子树插入节点造成不平衡
    2. 将α点跟α点的左儿子做单旋转
    3. 原先α点的左儿子的左子树根节点成为现在α点(之前的α点的左儿子)的左儿子，原先的α点作为现在α点的右儿子，原先α点的左儿子的右子树根节点成为现在α点的右儿子的左子树根节点
    4. 重新形成一个新的AVL树

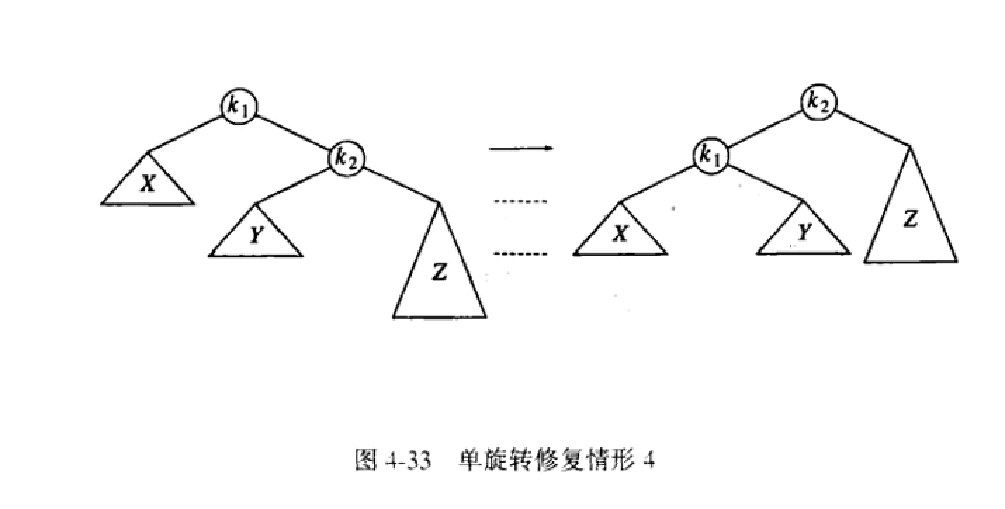
    image

    image

  • 对于情形4(如图4-33)，其实情形4跟情形差不多的做法就是方向改变了，我们需要将造成不平衡的插入点上移一层，另外那个跟它高度差为2的节点下移一层(就是将α点跟其右节点进行单旋转(单旋转就是类似将右节点拎起来，其他的节点根据重量下坠，然后再根据二叉查找树的特性排序形成新的平衡二叉树))，并形成新的平衡二叉查找树

    具体操作为：

    1. 向α点的右儿子的右子树插入节点造成不平衡
    2. 对α点跟α点的右儿子进行单旋转
    3. 原先的α点成为现在的α点(之前的α点的右儿子)的左儿子，原先的α点的右儿子的右子树根节点成为现在的α点的右儿子，原先α点的右儿子的左子树根节点成为了现在α点的左儿子的右子树根节点
    4. 重新形成一颗新的AVL树

    image

双旋转

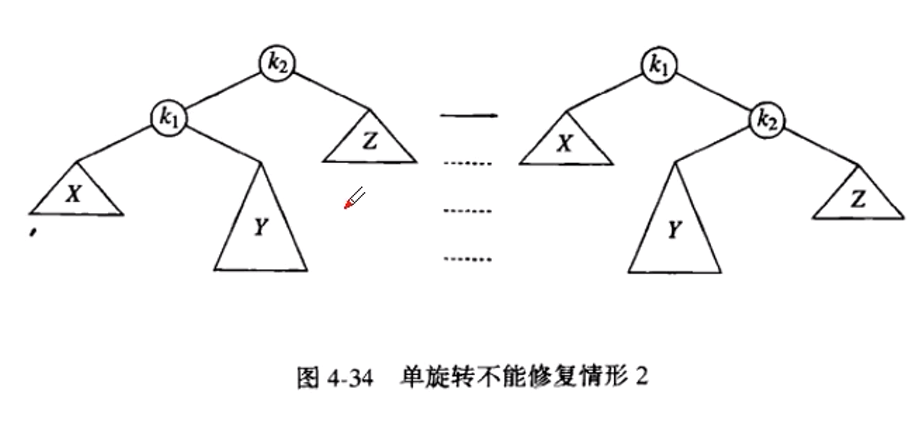
  • 对于情形2和3，单旋转无法修正被破坏的AVL树，对于图4-34子树Y太深，单旋转无法减低它的深度

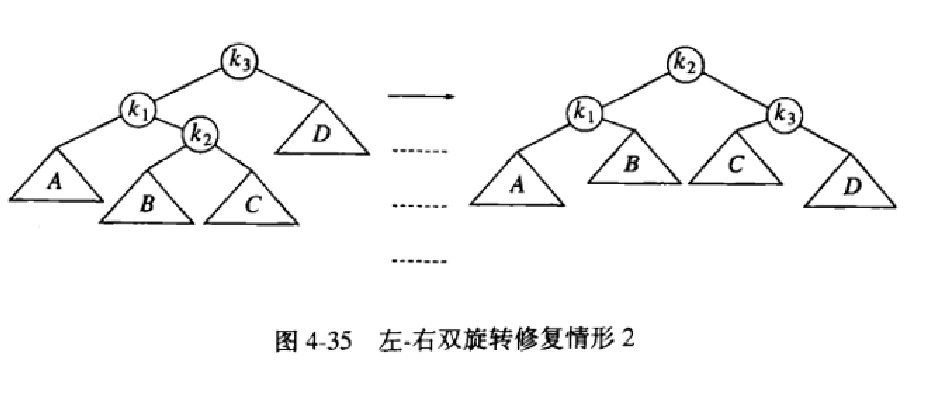
    image

  • 对于情形2，例如图4-35(k1<k2<k3)，我们需要用到双旋转(让α的左儿子的右子树根节点跟α的左儿子做一次单旋转，旋转完后，α的左儿子的右子树就是α的左儿子，原来α的左儿子变成了α的左儿子的右子树根节点，然后现在的α的左儿子(也就是原来的α的左儿子的右子树根节点)跟α点做一次单旋转)，具体步骤就是

    1. 向α的左儿子的右子树插入节点
    2. 就双旋转后，让α的左儿子的右子树根节点(这里成为k2)旋转到α点(这里称为k3)的位置，α的左儿子(称为k1)成为k2的左儿子，k3成为k2的右儿子
    3. 如果插入的是左节点，就让它成为k1的右儿子，如果插入的是右节点就让它成为k3的左儿子。
    4. 然后就形成了新的AVL树

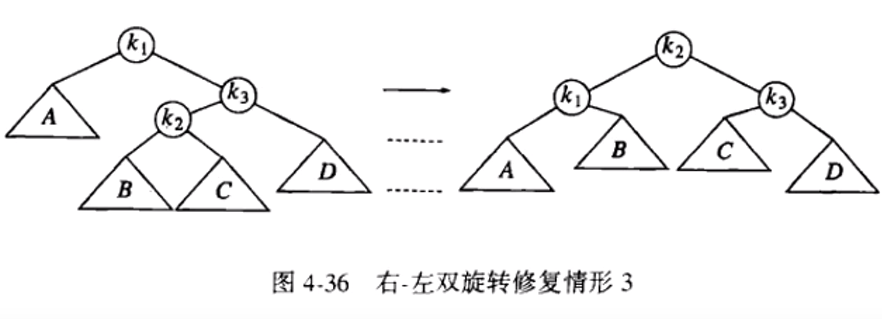
    image

  • 对于情形三(图4-36，k1<k2<k3)，跟情形二做法差不多只是方向改变了，我们需要用到双旋转(让α的右儿子的左子树根节点跟α的右儿子做一次单旋转，旋转完后，α的右儿子的左子树就是α的右儿子，原来α的右儿子变成了α的右儿子的左子树根节点，然后现在的α的右儿子(也就是原来的α的右儿子的左子树根节点)跟α点做一次单旋转)，具体步骤就是

    1. 向α的右儿子的左子树插入节点
    2. 就双旋转后，让α的右儿子的左子树根节点(这里成为k2)旋转到α点(这里称为k1)的位置，α的右儿子(称为k3)成为k2的右儿子，k1成为k2的左儿子
    3. 如果插入的是左节点，就让它成为k1的右儿子，如果插入的是右节点就让它成为k3的左儿子。
    4. 然后就形成了新的AVL树

    image

代码:

//平衡查找树是其每个节点的左子树和右子树的高度最多差1的二叉查找树
struct AVL{
    int data;
    AVL* left;
    AVL* right;
    int height;  //节点高度
};

AVL* createNode(int data){
    auto p=new AVL;
    p->data=data;
    p->right=NULL;
    p->left=NULL;
    p->height=0;
    return p;
}

//防止出现空的高度
int Height(AVL* root){
    if(root==NULL){
        return -1;
    }else{
        return root->height;
    }
}

//左左情况单旋转函数
AVL* SingleRotatewithLeft(AVL* &k1){
    AVL* k2;
    k2=k1->left;
    k1->left=k2->right;
    k2->right=k1;
    k1->height= max(Height(k1->left), Height(k1->right))+1;
    k2->height= max(Height(k2->left), Height(k2->right))+1;
    return k2;
}

//右右情况单旋转函数
AVL* SingleRotatewithRight(AVL* &k1){
    AVL* k2;
    k2=k1->right;
    k1->right=k2->left;
    k2->left=k1;
    k1->height= max(Height(k1->left), Height(k1->right))+1;
    k2->height= max(Height(k2->left), Height(k2->right))+1;
    return k2;
}

//左右情况双旋转
AVL* DoubleRotatewithLeft(AVL* &k1){
    //非递归形式
//    AVL* k2;
//    AVL* k3;
//    k2=k1->left;
//    k3=k1->left->right;
//    k1->left=k3->right;
//    k2->right=k3->left;
//    k3->left=k2;
//    k3->right=k1;
//    k1->height=max(Height(k1->left), Height(k1->right))+1;
//    k2->height=max(Height(k2->left), Height(k2->right))+1;
//    k3->height=max(Height(k3->left), Height(k3->right))+1;
//    return k3;
    //递归形式，建议用递归，好记
    k1->left= SingleRotatewithRight(k1->left);   //k2跟k3单旋转
    return SingleRotatewithLeft(k1);       //k1跟现在的k2(原来的k3)单旋转
}

//右左情况双旋转
AVL* DoubleRotatewithRight(AVL* &k1){
    //非递归形式
//    AVL* k2;
//    AVL* k3;
//    k2=k1->right;
//    k3=k1->right->left;
//    k1->right=k3->left;
//    k2->left=k3->right;
//    k3->left=k1;
//    k3->right=k2;
//    k1->height=max(Height(k1->left), Height(k1->right))+1;
//    k2->height=max(Height(k2->left), Height(k2->right))+1;
//    k3->height=max(Height(k3->left), Height(k3->right))+1;
//    return k3;
    //递归形式
    k1->right= SingleRotatewithLeft(k1->right);       //k2跟k3单旋转
    return SingleRotatewithRight(k1);           //k1跟现在的k2(原来的k3)单旋转
}


//插入
AVL* insert(AVL* &root,int data){
    if(NULL==root){
        AVL* add= createNode(data);
        root=add;
    }else if(data<root->data){
        root->left= insert(root->left,data);
        //判断高度差
        if(2== Height(root->left)- Height(root->right)){
            //左左情况，情形1,单旋转
            if(data<root->left->data){
                root=SingleRotatewithLeft(root);
            }else{   //左右情况，情形2，双旋转
                root=DoubleRotatewithLeft(root);
            }
        }
    }else if(data>root->data){
        root->right= insert(root->right,data);
        if(2== Height(root->right)- Height(root->left)){
            //右右情况，情形4，单旋转
            if(data>root->right->data){
                root=SingleRotatewithRight(root);
            }else{    //右左情况,情形3，双旋转
                root=DoubleRotatewithRight(root);
            }
        }
    }
    //通过递归，从后序开始往上回，这样就能保证树的高度的正确性,这样子到了根节点就拿到了最大的高度
    root->height= max(Height(root->left), Height(root->right))+1;
    return root;
}


//查找
AVL* Search(AVL* root,int data){
    if(NULL==root){
        return NULL;
    }
    if(data<root->data){
        root->left= Search(root->left,data);
    }else if(data>root->data){
        root->right= Search(root->right,data);
    }else
        return root;
}


//查找最小值
int findmin(AVL* root){
    //递归形式
    if(NULL==root){
        return root->data;
    }
    if(root->left!=NULL){
        return findmin(root->left);
    }else{
        return root->data;
    }

    //非递归形式
//    if(NULL!=root){
//        while (root->left!=NULL){
//            root=root->left;
//        }
//        return root->data
//    }
//    return NULL;
}

//查找最大值
int findmax(AVL* root){
    //递归形式
//    if(NULL==root){
//        return NULL;
//    }
//    if(NULL!=root->right){
//        return findmax(root->right);
//    }else{
//        return root->data;
//    }

    //非递归形式
    if(NULL!=root){
        while (root->right!=NULL){
            root=root->right;
        }
    }
    return root->data;
}


//删除节点，删除操作也会导致AVL树平衡破坏，所以删除操作也需要对AVL树做判断
AVL* del(AVL* &root,int data){
    if(NULL==root){
        return NULL;
    }else if(data<root->data){
        root->left= del(root->left,data);
        if(2== Height(root->left)- Height(root->right)){
            if(data<root->left->data){
                root= SingleRotatewithLeft(root);
            }else{
                root= DoubleRotatewithLeft(root);
            }
        }
    }else if(data>root->data){
        root->right=del(root->right,data);
        if(2== Height(root->right)- Height(root->left)){
            if(data>root->right->data){
                root= SingleRotatewithRight(root);
            }else{
                root= DoubleRotatewithRight(root);
            }
        }
    }else if(root->left&&root->right){
        int temp= findmin(root);
        root->data=temp;
        root->right=del(root->right,temp);
    }else{
        AVL* p=root;
        if(NULL==root->left){
            root=root->right;
        }else if(NULL==root->right){
            root=root->left;
        }
        delete p;
    }
    if(root!=NULL)
        root->height=max(Height(root->left), Height(root->right))+1;
    return root;
}


//清空树
void destroy(AVL* &root){
    if(NULL==root){
        return;
    }
    destroy(root->left);
    destroy(root->right);
    delete root;
}

//打印，中序遍历
void inorderprint(AVL* root){
    if(NULL==root){
        return;
    }
    inorderprint(root->left);
    cout<<root->data<<" ";
    inorderprint(root->right);
}

尾言

完整版笔记也就是数据结构与算法专栏完整版可到我的博客进行查看，或者在github库中自取(包含源代码)

悦读

道可道，非常道；名可名，非常名。 无名，天地之始，有名，万物之母。 故常无欲，以观其妙，常有欲，以观其徼。 此两者，同出而异名，同谓之玄，玄之又玄，众妙之门。

最新收录
React面试题目（从基本到高级）
Vue 文件导出和出现乱码解决方法
多线程多进程的python爬虫脚本项目（可爬起点小说VIP内容）
Neo4j（一）：图数据库基础
文件批量处理功能之——批量分发文件
java实现约瑟夫环问题
Tomcat配置Https
屏幕上1像素代表的实际距离是多少？
力扣93题：复原 IP 地址
【JavaScript】arr.join()和arr.split()方法
;