本文介绍一篇刚被数据挖掘国际顶级期刊TKDE 2023接收的regular paper
论文地址:
背景
多变量时间序列(Multivariable Time Series,MTS)普遍存在于各种现实场景中,例如城市交通流、股市股价和城市街区的家庭用电量。相比于单变量时间序列预测,多变量时间序列预测则需要同时考虑一个时间序列内的时间相关性以及变量间相关性(即单个变量的预测值会受到其他变量的影响)。
图是表示节点之间关系的抽象数据类型。图神经网络(GNN)可以有效地捕获节点的高阶表示,同时显式地利用成对的相关性,被认为是处理图数据的一种很有前途的方法。MTS预测可以从图建模的角度来考虑。MTS中的变量可以看作是图中的节点,而成对的变量间相关性可以看作是边。最近,一些研究利用图的丰富结构信息(即节点特征和加权边),结合GNN对MTS建模。这些工作将GNN和时间卷积模块结合起来学习时序模式,取得了很好的效果。然而,在上述工作中,仍有两个重要的方面被忽视。
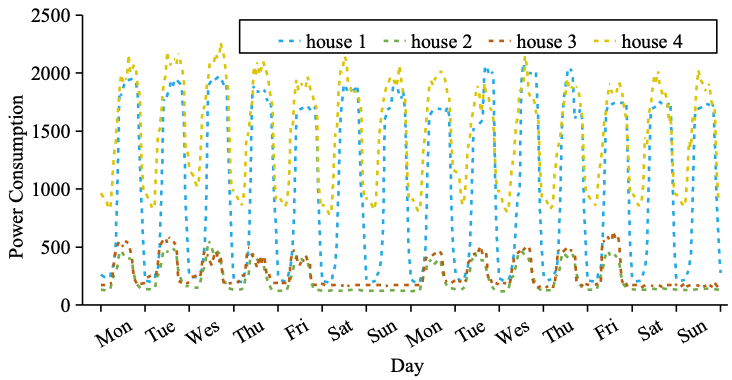
首先,现有的研究只考虑单个时间尺度上的时间相关性,这可能无法正确反映许多真实场景中的情况。事实上,现实世界中的MTS,其时序模式要复杂得多,包括每日、每周、每月和其他特定的周期模式。例如,图中显示了两周内4个家庭的用电量。存在短期和长期重复模式的混合(即每天和每周)。家庭1和4有每日和每周的重复模式,而家庭2和3有每周的重复模式。这些多尺度的时序模式为MTS预测提供了丰富的信息。此外,如果分别从不同的时间尺度上学习时序模式,然后直接拼接得到最终的表示,该模型无法捕捉跨尺度的关系,不能关注到最重要的时序模式。因此,一个准确的MTS预测模型需要学习一种能够综合反映多尺度时序模式的特征表示。
其次,现有的研究通过学习一个共享的邻接矩阵来表示丰富的变量间相关性,这使得模型倾向于学习一种显著的、共享的时序模式。事实上,现实场景中的多变量时间序列中通常存在局部、全局、物理、语义等多种类型的变量间相关性。如某个城市所有路口的交通流量时间序列中,路网相连的两个路口的交通流量时序模式会比较相似,而在实际路网距离较远,却位于相同的城市功能区中的两个路口,其交通流量时序模式也会比较相似。通过某种先验知识或人工经验定义的固定权重的邻接矩阵、或通过学习单个邻接矩阵,难以有效刻画那些隐式的多类型的变量间相关性。因此,在对这些多尺度时序模式进行建模时,需要充分考虑复杂的多类型的变量间相关性。
本文的贡献点如下:
· 提出了MAGNN,它学习了一种能够综合反映多尺度时序模式和多类型变量间相关性的特征表示。
· 设计了一个自适应图学习模块来探索丰富而隐含的多类型的变量间相关性,以及一个多尺度融合模块来建模尺度之间的相关性,并自动捕获所有时序模式的重要性。
· 在六个真实世界的MTS基准数据集上进行广泛的实验。实验结果表明,该方法的性能优于现有的方法。
整体框架
MAGNN的框架由四个主要部分组成:a)一个多尺度金字塔网络,以在不同的时间尺度上保留潜在的时序模式。每一层中,通过两个并行的卷积神经网络和逐位加法将特征表示从小尺度到大尺度进行逐级变换。b)自适应图学习模块,自动推断变量间相关性,以节点嵌入和尺度嵌入为输入,输出尺度相关的邻接矩阵。c)一种多尺度时序图神经网络,用于捕获各种尺度特定的时序模式,每个尺度特征表示和邻接矩阵被输入到一个时序图神经网络中,以获得尺度特定的表示。d)一个多尺度融合模块对尺度特定的表示进行加权,自动考虑每个尺度表示的重要性并捕获跨尺度相关性。
1)多尺度金字塔网络
多尺度金字塔网络来显式获取不同时间尺度下的时间相关性。在金字塔结构的基础上,应用多个金字塔层将原始时间序列层次化抽取从小尺度到大尺度的子序列。这种多尺度结构使模型能在不同的时间尺度上观察原始时间序列。具体来说,小尺度子序列可以保留更多的细粒度细节,而大尺度子序列可以捕捉缓慢变化的趋势。
多尺度金字塔网络通过堆叠多个金字塔层生成多尺度子序列。每个金字塔层将前一个金字塔层的输出作为输入,并生成更大尺度的子序列作为输出。
2)自适应图学习
自适应图学习模块自动生成邻接矩阵来表示MTS中的变量间相关性,现有的基于学习的方法只学习一个共享的邻接矩阵来建模各种时序模式。在许多问题中,共享邻接矩阵有助于学习MTS中最显著的时序模式,并能显著减少参数数目,避免过拟合问题。然而,当对多尺度时序模式建模时,这将导致次优的结果。短期模式的动态性往往受到相邻节点的影响,而长期模式往往由具有相似固有模式的节点反映。因此,学习多个邻接矩阵是十分有必要的。
但是,对于每个尺度直接学习一个特定的邻接矩阵会引入过多的参数,使得模型难以训练,特别是当节点数较大时。为了解决这一问题,本章提出了一种基于矩阵分解的自适应图学习(Adaptive Graph Learning,AGL)模块。AGL初始化两类参数:1)在所有尺度之间共享的节点嵌入;2)每个尺度的嵌入。从单个尺度的视角来看,可以提取尺度相关的变量间相关性,这种方式可以同时捕获共享的信息和尺度相关信息。
3)多尺度时序图神经网络
近年来,时间卷积网络(TCN)在时间序列建模方面显示出了优越性。因此,提出了一种结合GNN和时间卷积层的解决方案,即用时间卷积层代替GRU。
具体地说,MTG由个时序图神经网络组成,每个时序图神经网络结合TCN和GNN来捕获该尺度下的时序模式。
4)多尺度融合
为了获得最终的多尺度表示,一种直观的解决方案是直接串接这些尺度特定的表示或通过全局的池化层聚合这些表示。然而,这种解决方案平等地对待每一个尺度的表示,忽略了每个尺度表示在对最终预测结果的贡献上的差异。例如,小尺度表示对于短期预测更为重要,而大尺度表示对于长期预测更为重要。因此,提出了一个多尺度融合模块,从这些尺度特定的表示中学习鲁棒的多尺度表示,该模块可以考虑尺度特定的时序模式的重要性,并捕获跨尺度的相关性。
实验结果
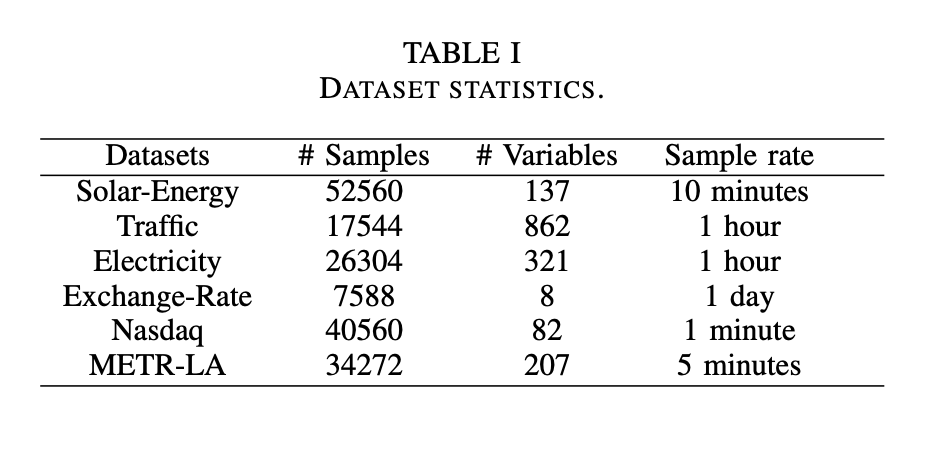
在六个公开的数据集上进行了实验:
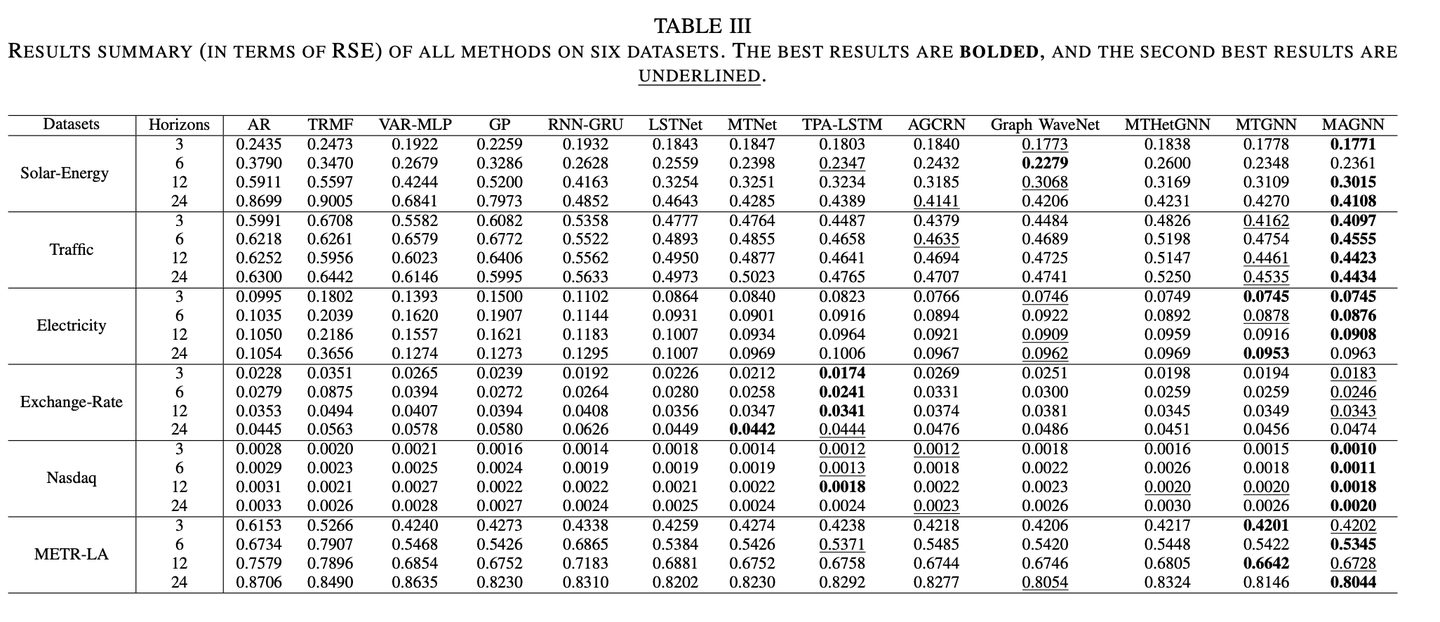
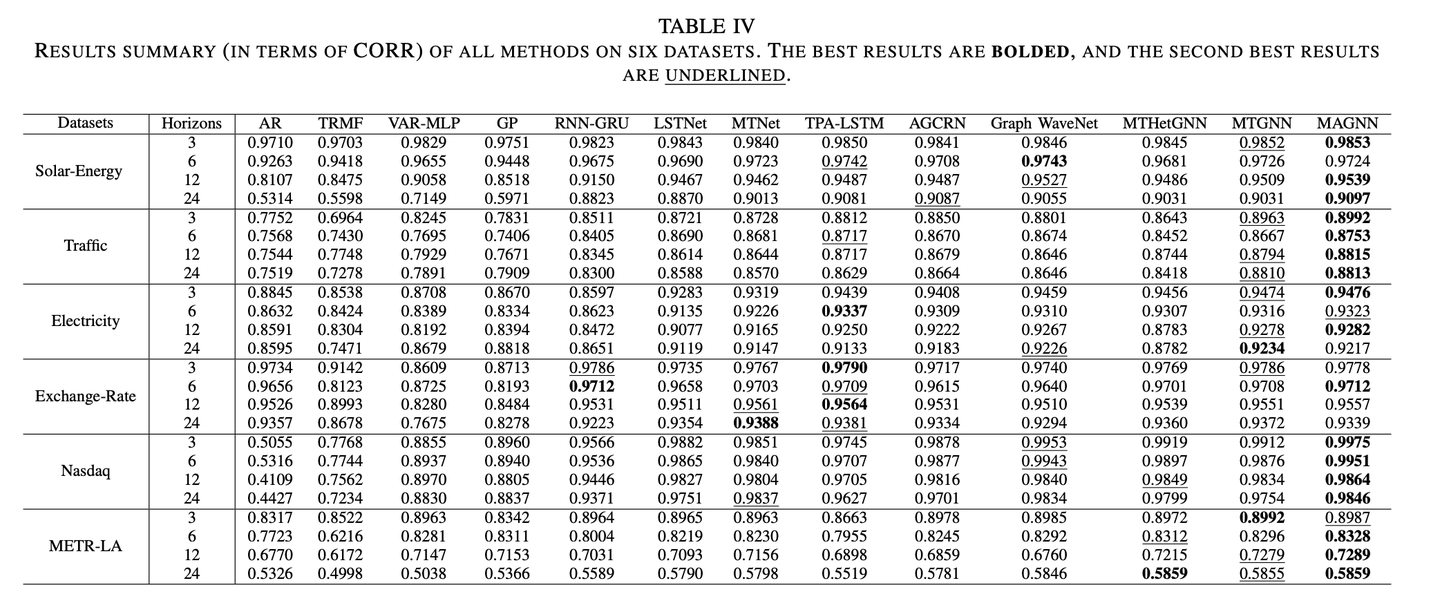
和现有方法的对比(采用了RSE和CORR两个评价指标):