强化学习经典算法笔记(六)：深度Q值网络 Deep Q Network

前期回顾

强化学习经典算法笔记(零)：贝尔曼方程的推导
 强化学习经典算法笔记(一)：价值迭代算法Value Iteration
强化学习经典算法笔记(二)：策略迭代算法Policy Iteration
强化学习经典算法笔记(三)：蒙特卡罗方法Monte Calo Method
强化学习经典算法笔记(四)：时间差分算法Temporal Difference（Q-Learning算法）
强化学习经典算法笔记(五)：时间差分算法Temporal Difference（SARSA算法）

强化学习经典算法笔记——深度Q值网络

到这里，我们终于来到了深度强化学习的领域了，之前的算法都是经典RL算法，它们和DRL的关系好比是机器学习和深度学习的关系。深度神经网络的引入极大地提升了强化学习算法的效率和能力，使强化学习的研究进入了新的阶段。

简介

深度强化学习的经典之作是2015年DeepMind发表在Nature的DQN论文《Human-Level Control Through Deep Reinforcement Learning》。本篇博客就讲一讲DQN的基本框架思想，并用代码实现它。

DQN属于Q-Learning算法，也是一种Value-Based算法，并不直接学习一个Policy，而是学习Critic，也就是学习如何评价当前状态的好坏，进而根据Q值选取最佳的action。因此可以将DQN中的神经网络看做是一个复杂的Q-function，本质上，它和前几篇中提到的Q-table干的事是一样的，只不过神经网络的函数拟合能力很强，它能胜任更复杂的RL任务。

我个人观点，深度强化学习的框架大致可以分为两部分，一部分是感知（Sensoring），另一部分是决策（Decision Making）。

DRL往往需要学习一个感知算法，感知真实环境的各种信息。有的感知器输出一个标量，反映当前环境或状态动作对的好坏；有的感知器则是对真实环境进行建模，将当前状态抽象成一个隐层特征，用于后续的决策算法使用，这类算法有DeepMind的World Model和PlaNet系列，我们以后都会讲到。

感知算法是对真实环境的总结和特征提取，要想做出决策，还需要一个决策算法。比如DQN中的 $\epsilon-greedy$ 算法，虽然是一个比较简单的policy算法，直接采取具有最大Q值的动作作为当前策略，但是我们也可以看做是一个决策算法，它利用了上一步的感知器对环境的感知信息。

再比如，AlphaGo系列算法中，CNN负责对当前棋盘状态提取特征，给出当前胜算（也就是评估当前状态好坏），接着蒙特卡洛树搜索算法根据CNN输出的Q值计算子结点的U值，进行棋盘搜索，完成决策。

从感知和决策的角度审视深度强化学习，深度神经网络的引入提升了感知和决策两方面的效果。我们在这一篇主要讲神经网络对感知能力的提升，而将神经网络用于决策的内容放到后面去讲。但是，将神经网络用于强化学习早已有之，不过效果一直不好，直到DQN引入了几个核心技术，才将性能大大提升，即

卷积神经网络 CNN
目标网络 Target Network
经验回放 Experience Replay

DQN应该是第一个采用原始图像作为CNN输入进行训练的，也应该是第一个将CNN在RL发挥巨大威力的算法。DQN中的CNN采用和AlexNet类似的结构。

目标网络是DQN的一大贡献。我们知道，与环境交互具有极大的随机性，XXXXXXXXXXXXXXXXX

经验回放是DQN的另一贡献。我们知道，一个episode是一个时间关联性很强的（状态-动作-回报）序列，如果直接拿若干个episode的序列数据来训练CNN，XXXXXXXXXXXXXXXXXXXXXXX

现在让我们看看DQN完整的算法

以下操作执行N个Episode：

将游戏画面 $s$ 进行预处理，送入CNN，输出每个动作的Q值
根据 $\epsilon-greedy$ 算法计算应该采取的动作 $a=argmax(Q(s,a,\theta))$
执行动作 $a$ ，转移到下一状态 $s^{'}$ ，收到环境给出的回报
将序列 $< s, a, r, s^{'} >$ 存入经验池
从经验池采样一个batch的数据，训练Q Network，实际上是一个由输入预测输出的回归问题
$loss=(r+\gamma max_{a'}Q(s',a';\theta')-Q(s,a;\theta))^2$
CNN（当前网络）训练若干代之后，将其参数拷贝给目标网络。

DQN实验

本次实验采用的游戏环境是MrPacman-v0。这个游戏很简单，控制小人吃掉路上的小长方块，同时躲避怪物的接触。每吃一个小块得10分，碰到怪物就会丢掉命，一局游戏有三条命，每条命的得分是累加的。算法的目标就是取得尽可能高的分数

导入必要的环境依赖。

import numpy as np
import gym
import tensorflow as tf
from tensorflow.contrib.layers import flatten, conv2d, fully_connected
from collections import deque, Counter
import random
import matplotlib.pyplot as plt
%matplotlib inline

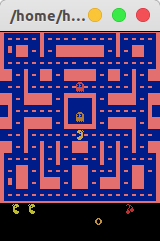
游戏环境给出的observation是210x160x3的彩色图像，如下图。

env = gym.make('MsPacman-v0')
env.render()
# env.close()

在这里插入图片描述
游戏的动作有九个——等待、右转、左转、向上、向下、向左移动、向右移动、向上移动和向下移动，所以我们之后要搭建的神经网络的输出也有9个。

n_outputs = env.action_space.n
# n_outputs = 9

我们首先对图像进行预处理。具体包括裁剪、降采样、灰度化和提高对比度。

# color后面用于图像的锐化
color = np.array([210, 164, 74]).mean()

def preprocess_observation(obs):
	'''
	处理210x160x3图像
	'''
    # 以2为步长，截取1-176行的像素，共取88行
    # 同样地，每两列取1列像素，共取80列
    # img.shape = (88,80,3)
    img = obs[1:176:2, ::2]
	
    # 彩图转灰度图，即对三通道像素值取平均
    img = img.mean(axis=2)

    # 提高图像对比度
    img[img==color] = 0

    # 像素值归一化(-1,1)
    img = (img - 128) / 128 - 1

    return img.reshape(88,80,1)

处理过后的图像
在这里插入图片描述
下面来搭建DQN的核心——CNN。根据Q function的定义，Q值是评估一个状态动作对的好坏的，但是在实现算法时，状态（一个矩阵）非常适合作为CNN的输入，但是动作是一个标量，和状态同时输入CNN不好实现，所以我们实际做的是输入一个游戏状态的图像，输出所有动作的Q值。

tf.reset_default_graph()

def q_network(X, name_scope):
    
    # Initialize layers
    initializer = tf.contrib.layers.variance_scaling_initializer()

    with tf.variable_scope(name_scope) as scope: 

        # 定义卷积操作
        layer_1 = conv2d(X, num_outputs=32, kernel_size=(8,8), stride=4, padding='SAME', weights_initializer=initializer) 
        # summary.histogram的作用是在tensorboard中以直方图的形式可视化这个变量
        tf.summary.histogram('layer_1',layer_1)
        
        layer_2 = conv2d(layer_1, num_outputs=64, kernel_size=(4,4), stride=2, padding='SAME', weights_initializer=initializer)
        tf.summary.histogram('layer_2',layer_2)
        
        layer_3 = conv2d(layer_2, num_outputs=64, kernel_size=(3,3), stride=1, padding='SAME', weights_initializer=initializer)
        tf.summary.histogram('layer_3',layer_3)
        
        # 将2维feature map拉成向量，送入全连接层
        flat = flatten(layer_3)

        fc = fully_connected(flat, num_outputs=128, weights_initializer=initializer)
        tf.summary.histogram('fc',fc)
        
        # 最后一层全连接的输出是9个可能动作的Q值，注意这里没有经过激活函数，可以试一下softmax函数的效果
        output = fully_connected(fc, num_outputs=n_outputs, activation_fn=None, weights_initializer=initializer)
        tf.summary.histogram('output',output)
        
		
        # 将网络的权重保存起来，以便拷贝给Target Network
        vars = {v.name[len(scope.name):]: v for v in tf.get_collection(key=tf.GraphKeys.TRAINABLE_VARIABLES, scope=scope.name)} 
        return vars, output

下面创建 $\epsilon-greedy$ 策略，与之前不同，算法的 $\epsilon$ 是随着训练代数的增加而线性递减的。训练初期，策略更接近随机探索，训练后期，策略倾向于选择具有最优Q值的动作。请注意，当训练的episode数改变后，eps_decay_steps的值也要相应改变，使epsilon随着整个训练过程合理地减小。这一点在代码中也有说明。

eps_min = 0.05
eps_max = 1.0
# 每个episode约持续600-700个step
# 因此eps_decay_steps要随着num_episodes的变化而变化
eps_decay_steps = 500000

def epsilon_greedy(action, step):
    '''
	step = 0,epsilon=1
	step = 500000,epsilon = 0.05
	线性衰减
	'''
    epsilon = max(eps_min, eps_max - (eps_max-eps_min) * step/eps_decay_steps)
    if np.random.rand() < epsilon:
    	# 输出随机动作epsilon_greedy
        return np.random.randint(n_outputs)
    else:
    	# 输出最优动作
        return action

现在感知算法和决策算法都具备了，还差数据集。我们需要将 $(s, a, r, s^{'})$ 这样的数据存入经验池（experience replay buffer）。buffer不能用简单的list来充当，否则随着训练代数的增加，有可能内存会溢出。我们希望buffer具有线性表的各种特点，支持入队、出对，能设置最大长度。这个功能Python已经帮我们实现了，就是deque。

# from collections import deque, Counter
buffer_len = 20000
exp_buffer = deque(maxlen=buffer_len)

有了经验池，下一步就需要从经验池中取出数据，用于训练CNN。所以还要写一个sample_memories函数。

def sample_memories(batch_size):
	# permutation的作用:
	# 将[0, len(exp_buffer)-1] 的整数乱序排列
	# [:batch_size]取打乱顺序的buffer中1个batch的数据 
    perm_batch = np.random.permutation(len(exp_buffer))[:batch_size]
    mem = np.array(exp_buffer)[perm_batch]
    
    # 一条数据中包括(s,a,s',r,done) 5个数据
    return mem[:,0], mem[:,1], mem[:,2], mem[:,3], mem[:,4]

下面我们需要配置网络训练相关的超参数。

num_episodes = 800              # 一共玩800盘游戏
batch_size = 48                 # 每次从经验池拿出48个样本训练CNN
input_shape = (None, 88, 80, 1) # 网络输入尺寸，第1维是batch
learning_rate = 0.001 
X_shape = (None, 88, 80, 1)
discount_factor = 0.97          # 折扣率，表示未来回报对现在的重要程度

global_step = 0                 # 将每局游戏走的步数相累加，就是全局步数
copy_steps = 100                # 每100代,当前网络向Target Network拷贝参数
steps_train = 4                 # 设定游戏中每走4步，就训练CNN一次
start_steps = 2000              # 训练初期，经验池不满，所以前2000代先收集数据，不进行训练

# 在当前目录下新建logs文件夹,记录训练数据
logdir = 'logs'
tf.reset_default_graph()

# 定义送入CNN数据的接口
X = tf.placeholder(tf.float32, shape=X_shape)

# 用一个布尔值控制训练/非训练状态
in_training_mode = tf.placeholder(tf.bool)

创建2个CNN，一个Main CNN，一个Target CNN。

# main Q network
mainQ, mainQ_outputs = q_network(X, 'mainQ')

# target Q network
targetQ, targetQ_outputs = q_network(X, 'targetQ')

计算Q值。前面讲到，网络输入s，输出9个动作分别的Q值，也就是1个9维向量，但实际上我们希望的是输入(s,a)，输出Q(s,a)，所以需要在9维向量中取出我们真正想要的那个值，也就是数据 $(s, a, r, s^{'})$ 中真正的a对应的Q值。

为此我们定义X_action接口，对应的是exp buffer中的action，当然其长度是batch_size，因为我们在训练中一次取batch_size个样本，每1个元素都表示当时采取的动作(0-8)。将action从0-8转换成one-hot码，如 $(0, 0, 0, 1, 0, 0, 0, 0, 0)$ ，然后将CNN输出的9维向量，比如 $(1, 2, 3, 4, 5, 6, 7, 8, 9)$ 与one-hot相乘，就得 $(0, 0, 0, 4, 0, 0, 0, 0, 0)$ ，再求和得到4。到这里，我们算出了数据样本 $(s, a, r, s^{'})$ 中 $(s, a)$ 的CNN估值。将这个值记为Q_action。

# X_action 长度 = batch_size(48), 每1个元素都表示当时采取的动作0-8
X_action = tf.placeholder(tf.int32, shape=(None,))
# Q_action 长度 = batch_size
# Q_action计算的是样本中(s,a)的CNN估计的Q值
# (0,0,0,1,0,0,0,0,0)        *     (1,2,3,4,5,6,7,8,9)   =   (0,0,0,4,0,0,0,0,0) ==sum==> 4
# one_hot(X_action,9)    *       targetQ_outputs    ======  tf.reduce_sum ======>Q_action        
Q_action = tf.reduce_sum(targetQ_outputs * tf.one_hot(X_action, n_outputs), axis=-1, keep_dims=True)

定义拷贝参数的操作

copy_op = [tf.assign(main_name, targetQ[var_name]) for var_name, main_name in mainQ.items()]
copy_target_to_main = tf.group(*copy_op)

定义优化算法和loss function

# y相当于r+γ*max(Q(s,a))
y = tf.placeholder(tf.float32, shape=(None,1))

# 训练任务相当于一个回归问题，让CNN计算出来的值Q_action越来越接近r+γ*max(Q(s,a))
loss = tf.reduce_mean(tf.square(y - Q_action))

# Adam算法用于优化
optimizer = tf.train.AdamOptimizer(learning_rate)
training_op = optimizer.minimize(loss)

# 全局参数的初始化器
init = tf.global_variables_initializer()

loss_summary = tf.summary.scalar('LOSS', loss)

# summary.merge_all()可以将几乎所有数据放在tensorboard上显示
merge_summary = tf.summary.merge_all()

# 写入训练记录文件
file_writer = tf.summary.FileWriter(logdir, tf.get_default_graph())

下面就是正式开始训练的时候了。

with tf.Session() as sess:
    init.run() # 参数初始化
    
    # for循环持续num_episode盘游戏
    for i in range(num_episodes):
        done = False # 该局游戏是否结束的标志
        obs = env.reset() # 初始化游戏环境
        epoch = 0 # 在游戏中每走1步  = 一个global_step = 一个epoch
        episodic_reward = 0 # 每局游戏的总回报
        actions_counter = Counter()  # 一局游戏中0-8共9种动作分别执行的次数
        episodic_loss = [] # 记录一局游戏中每次训练CNN时的loss

        # 进入循环，直到游戏结束
        while not done:
			# 可视化游戏界面
            env.render()
        
            # 对游戏界面做图像预处理，obs.shape=(88,80,1)
            obs = preprocess_observation(obs)

            # 将当前obs送入CNN得到每个动作的Q值
            actions = mainQ_outputs.eval(feed_dict={X:[obs], in_training_mode:False})

            # 选Q值最大的action
            action = np.argmax(actions, axis=-1)
            # 记录当前选择的action
            actions_counter[str(action)] += 1 

            # 利用epsilon-greedy策略选择动作
            action = epsilon_greedy(action, global_step)
            
            # 执行动作，得到下一个状态、回报、是否结束的标志
            next_obs, reward, done, _ = env.step(action)
            
            # 将(s,a,r,s',done)作为一条exp存入经验池
            exp_buffer.append([obs, action, preprocess_observation(next_obs), reward, done])
            
            # 前start_steps(2000)次迭代只搜集数据，不训练CNN
            # 每4次迭代训练一次CNN，steps_train=4
            if global_step % steps_train == 0 and global_step > start_steps:
                
                # 从经验池中采样batch_size条数据
                o_obs, o_act, o_next_obs, o_rew, o_done = sample_memories(batch_size)

                # 当前状态，shape=(batch_size, 88, 80, 1)
                o_obs = [x for x in o_obs]
                # 下一状态
                o_next_obs = [x for x in o_next_obs]

                # 由o_next_obs计算的下一状态时，9个动作的Q值，shape=(batch_size, 9)
                next_act = mainQ_outputs.eval(feed_dict={X:o_next_obs, in_training_mode:False})


                # 利用时间差分算法计算当前真实回报，当游戏结束时刻，只有第1项o_rew，而无未来收益discount_factor * np.max(next_act, axis=-1)
                y_batch = o_rew + discount_factor * np.max(next_act, axis=-1) * (1-o_done) 

                # 保存所有训练过程中数据
                mrg_summary = merge_summary.eval(feed_dict={X:o_obs, y:np.expand_dims(y_batch, axis=-1), X_action:o_act, in_training_mode:False})
                file_writer.add_summary(mrg_summary, global_step)

                # 计算loss，训练CNN
                train_loss, _ = sess.run([loss, training_op], feed_dict={X:o_obs, y:np.expand_dims(y_batch, axis=-1), X_action:o_act, in_training_mode:True})
                episodic_loss.append(train_loss)
                # print(sess.run(X_action,feed_dict={X_action:o_act}))
            	# print(sess.run(Q_action,feed_dict={X_action:o_act,targetQ_outputs:next_act}))
            # 经过100次迭代，将main Q network权重拷贝给target Q network
            if (global_step+1) % copy_steps == 0 and global_step > start_steps:
                copy_target_to_main.run()
                
            obs = next_obs
            epoch += 1
            global_step += 1
            episodic_reward += reward
        
        print('Episode',i,'Epoch', epoch, 'Reward', episodic_reward,'Buffer len',len(exp_buffer))

代码完整版

import numpy as np
import gym
import tensorflow as tf
from tensorflow.contrib.layers import flatten, conv2d, fully_connected
from collections import deque, Counter
import random
import matplotlib.pyplot as plt
%matplotlib inline

env = gym.make('MsPacman-v0')

n_outputs = env.action_space.n
# n_outputs = 9

# color后面用于图像的锐化
color = np.array([210, 164, 74]).mean()

def preprocess_observation(obs):
	'''
	处理210x160x3图像
	'''
    # 以2为步长，截取1-176行的像素，共取88行
    # 同样地，每两列取1列像素，共取80列
    # img.shape = (88,80,3)
    img = obs[1:176:2, ::2]
	
    # 彩图转灰度图，即对三通道像素值取平均
    img = img.mean(axis=2)

    # 提高图像对比度
    img[img==color] = 0

    # 像素值归一化(-1,1)
    img = (img - 128) / 128 - 1

    return img.reshape(88,80,1)

tf.reset_default_graph()

def q_network(X, name_scope):
    
    # Initialize layers
    initializer = tf.contrib.layers.variance_scaling_initializer()

    with tf.variable_scope(name_scope) as scope: 

        # 定义卷积操作
        layer_1 = conv2d(X, num_outputs=32, kernel_size=(8,8), stride=4, padding='SAME', weights_initializer=initializer) 
        # summary.histogram的作用是在tensorboard中以直方图的形式可视化这个变量
        tf.summary.histogram('layer_1',layer_1)
        
        layer_2 = conv2d(layer_1, num_outputs=64, kernel_size=(4,4), stride=2, padding='SAME', weights_initializer=initializer)
        tf.summary.histogram('layer_2',layer_2)
        
        layer_3 = conv2d(layer_2, num_outputs=64, kernel_size=(3,3), stride=1, padding='SAME', weights_initializer=initializer)
        tf.summary.histogram('layer_3',layer_3)
        
        # 将2维feature map拉成向量，送入全连接层
        flat = flatten(layer_3)

        fc = fully_connected(flat, num_outputs=128, weights_initializer=initializer)
        tf.summary.histogram('fc',fc)
        
        # 最后一层全连接的输出是9个可能动作的Q值，注意这里没有经过激活函数，可以试一下softmax函数的效果
        output = fully_connected(fc, num_outputs=n_outputs, activation_fn=None, weights_initializer=initializer)
        tf.summary.histogram('output',output)
        
		
        # 将网络的权重保存起来，以便拷贝给Target Network
        vars = {v.name[len(scope.name):]: v for v in tf.get_collection(key=tf.GraphKeys.TRAINABLE_VARIABLES, scope=scope.name)} 
        return vars, output


eps_min = 0.05
eps_max = 1.0
# 每个episode约持续600-700个step
# 因此eps_decay_steps要随着num_episodes的变化而变化
eps_decay_steps = 500000

def epsilon_greedy(action, step):
    '''
	step = 0,epsilon=1
	step = 500000,epsilon = 0.05
	线性衰减
	'''
    epsilon = max(eps_min, eps_max - (eps_max-eps_min) * step/eps_decay_steps)
    if np.random.rand() < epsilon:
    	# 输出随机动作epsilon_greedy
        return np.random.randint(n_outputs)
    else:
    	# 输出最优动作
        return action

# from collections import deque, Counter
buffer_len = 20000
exp_buffer = deque(maxlen=buffer_len)

def sample_memories(batch_size):
	# permutation的作用:
	# 将[0, len(exp_buffer)-1] 的整数乱序排列
	# [:batch_size]取打乱顺序的buffer中1个batch的数据 
    perm_batch = np.random.permutation(len(exp_buffer))[:batch_size]
    mem = np.array(exp_buffer)[perm_batch]
    
    # 一条数据中包括(s,a,s',r,done) 5个数据
    return mem[:,0], mem[:,1], mem[:,2], mem[:,3], mem[:,4]


num_episodes = 800              # 一共玩800盘游戏
batch_size = 48                 # 每次从经验池拿出48个样本训练CNN
input_shape = (None, 88, 80, 1) # 网络输入尺寸，第1维是batch
learning_rate = 0.001 
X_shape = (None, 88, 80, 1)
discount_factor = 0.97          # 折扣率，表示未来回报对现在的重要程度

global_step = 0                 # 将每局游戏走的步数相累加，就是全局步数
copy_steps = 100                # 每100代,当前网络向Target Network拷贝参数
steps_train = 4                 # 设定游戏中每走4步，就训练CNN一次
start_steps = 2000              # 训练初期，经验池不满，所以前2000代先收集数据，不进行训练

# 在当前目录下新建logs文件夹,记录训练数据
logdir = 'logs'
tf.reset_default_graph()

# 定义送入CNN数据的接口
X = tf.placeholder(tf.float32, shape=X_shape)

# 用一个布尔值控制训练/非训练状态
in_training_mode = tf.placeholder(tf.bool)

# main Q network
mainQ, mainQ_outputs = q_network(X, 'mainQ')

# target Q network
targetQ, targetQ_outputs = q_network(X, 'targetQ')

# X_action 长度 = batch_size(48), 每1个元素都表示当时采取的动作0-8
X_action = tf.placeholder(tf.int32, shape=(None,))
# Q_action 长度 = batch_size
# Q_action计算的是样本中(s,a)的CNN估计的Q值
# (0,0,0,1,0,0,0,0,0)        *     (1,2,3,4,5,6,7,8,9)   =   (0,0,0,4,0,0,0,0,0) ==sum==> 4
# one_hot(X_action,9)    *       targetQ_outputs    ======  tf.reduce_sum ======>Q_action        
Q_action = tf.reduce_sum(targetQ_outputs * tf.one_hot(X_action, n_outputs), axis=-1, keep_dims=True)



copy_op = [tf.assign(main_name, targetQ[var_name]) for var_name, main_name in mainQ.items()]
copy_target_to_main = tf.group(*copy_op)



# y相当于r+γ*max(Q(s,a))
y = tf.placeholder(tf.float32, shape=(None,1))

# 训练任务相当于一个回归问题，让CNN计算出来的值Q_action越来越接近r+γ*max(Q(s,a))
loss = tf.reduce_mean(tf.square(y - Q_action))

# Adam算法用于优化
optimizer = tf.train.AdamOptimizer(learning_rate)
training_op = optimizer.minimize(loss)

# 全局参数的初始化器
init = tf.global_variables_initializer()

loss_summary = tf.summary.scalar('LOSS', loss)

# summary.merge_all()可以将几乎所有数据放在tensorboard上显示
merge_summary = tf.summary.merge_all()

# 写入训练记录文件
file_writer = tf.summary.FileWriter(logdir, tf.get_default_graph())


with tf.Session() as sess:
    init.run() # 参数初始化
    
    # for循环持续num_episode盘游戏
    for i in range(num_episodes):
        done = False # 该局游戏是否结束的标志
        obs = env.reset() # 初始化游戏环境
        epoch = 0 # 在游戏中每走1步  = 一个global_step = 一个epoch
        episodic_reward = 0 # 每局游戏的总回报
        actions_counter = Counter()  # 一局游戏中0-8共9种动作分别执行的次数
        episodic_loss = [] # 记录一局游戏中每次训练CNN时的loss

        # 进入循环，直到游戏结束
        while not done:
			# 可视化游戏界面
            env.render()
        
            # 对游戏界面做图像预处理，obs.shape=(88,80,1)
            obs = preprocess_observation(obs)

            # 将当前obs送入CNN得到每个动作的Q值
            actions = mainQ_outputs.eval(feed_dict={X:[obs], in_training_mode:False})

            # 选Q值最大的action
            action = np.argmax(actions, axis=-1)
            # 记录当前选择的action
            actions_counter[str(action)] += 1 

            # 利用epsilon-greedy策略选择动作
            action = epsilon_greedy(action, global_step)
            
            # 执行动作，得到下一个状态、回报、是否结束的标志
            next_obs, reward, done, _ = env.step(action)
            
            # 将(s,a,r,s',done)作为一条exp存入经验池
            exp_buffer.append([obs, action, preprocess_observation(next_obs), reward, done])
            
            # 前start_steps(2000)次迭代只搜集数据，不训练CNN
            # 每4次迭代训练一次CNN，steps_train=4
            if global_step % steps_train == 0 and global_step > start_steps:
                
                # 从经验池中采样batch_size条数据
                o_obs, o_act, o_next_obs, o_rew, o_done = sample_memories(batch_size)

                # 当前状态，shape=(batch_size, 88, 80, 1)
                o_obs = [x for x in o_obs]
                # 下一状态
                o_next_obs = [x for x in o_next_obs]

                # 由o_next_obs计算的下一状态时，9个动作的Q值，shape=(batch_size, 9)
                next_act = mainQ_outputs.eval(feed_dict={X:o_next_obs, in_training_mode:False})


                # 利用时间差分算法计算当前真实回报，当游戏结束时刻，只有第1项o_rew，而无未来收益discount_factor * np.max(next_act, axis=-1)
                y_batch = o_rew + discount_factor * np.max(next_act, axis=-1) * (1-o_done) 

                # 保存所有训练过程中数据
                mrg_summary = merge_summary.eval(feed_dict={X:o_obs, y:np.expand_dims(y_batch, axis=-1), X_action:o_act, in_training_mode:False})
                file_writer.add_summary(mrg_summary, global_step)

                # 计算loss，训练CNN
                train_loss, _ = sess.run([loss, training_op], feed_dict={X:o_obs, y:np.expand_dims(y_batch, axis=-1), X_action:o_act, in_training_mode:True})
                episodic_loss.append(train_loss)
                # print(sess.run(X_action,feed_dict={X_action:o_act}))
            	# print(sess.run(Q_action,feed_dict={X_action:o_act,targetQ_outputs:next_act}))
            # 经过100次迭代，将main Q network权重拷贝给target Q network
            if (global_step+1) % copy_steps == 0 and global_step > start_steps:
                copy_target_to_main.run()
                
            obs = next_obs
            epoch += 1
            global_step += 1
            episodic_reward += reward
        
        print('Episode',i,'Epoch', epoch, 'Reward', episodic_reward,'Buffer len',len(exp_buffer))

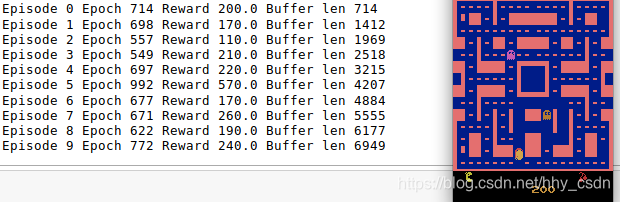
开始训练，如下图。大功告成，下一篇讲讲DQN实验的细节，如何在Tensorboard上查看训练日志，以及如何搭建更复杂的模型以提高性能。

在这里插入图片描述