【KMP 算法】
(一)KMP 算法简介
KMP 算法是由克努特(Knuth)、莫里斯(Morris)和普拉特(Pratt)共同设计实现的,因此简称 KMP 算法。此算法可以在 O(n+m) 的时间数量级上完成串的模式匹配操作。KMP 算法中模式串 T 的 next 数组,是 KMP 算法的核心。
KMP 算法中的 next 数组仅取决于模式串本身,而与相匹配的主串无关。
next 数组的核心作用是“当模式串 T 的第 j 位与主串 S 的第 pos 位失配时(即 T[j]≠S[pos] 时),让模式串 T 的第 next[j] 位与主串 S 的第 pos 位再进行比较”。这相当于让模式串 T 往右移动了 j-next[j] 位后,再进行比较。
(二)KMP 算法中的 next 数组:https://blog.csdn.net/hnjzsyjyj/article/details/127086502
● 在 KMP 算法的众多实现中,有多种定义 next 数组的方式。所以在使用和查看别人代码时,要特别注意 KMP 算法的 next 数组的定义,以免发生混淆。如:
(1)严蔚敏《数据结构》将模式串下标从 1 开始计数,故定义 next[1]=0,next[2]=1;
(2)李春葆《数据结构》将模式串下标从 0 开始计数,故定义 next[0]=-1,next[1]=0。
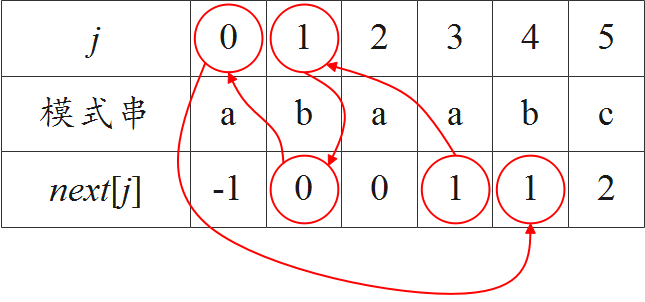
但这两种定义方式,不影响它们有一致的计算方法,即“若第 j-1 位的字符与第 x 位的字符相等,则 next[j]=x+1”(特别注意:在此判别过程中,所谓的第 x 位是由已经计算出的 next[j-1] 跳转抵达)。
● 由于字符串的下标在 C++ 中从 0 开始,因此在利用 C++ 进行 KMP 算法的设计中,将 next 数组下标从 0 开始考虑,是很自然的事情。据此,建议选择李春葆《数据结构》中关于模式串下标的定义,即从 0 开始考虑,据此可定义 next[0]=-1,next[1]=0。之后,按照“(1)若第 i-1 位的字符与第 j 位的字符相等,则 next[i]=j+1;(2)若直到第 0 位依然没有字符与第 i-1 位的字符相等,则 next[i]=0”构建 next 数组。
● 求 next 数组的算法代码:https://blog.csdn.net/hnjzsyjyj/article/details/127114683
(1)李春葆定义法next数组值的算法代码
#include<iostream>
using namespace std;
const int maxn=100;
int ne[maxn];
void getNext(string s) {
int len=s.length();
int i=0, j=-1;
ne[0]=-1;
while(i<len) {
if(j==-1 || s[i]==s[j]) {
ne[++i]=++j;
} else j=ne[j];
}
}
int main() {
string T;
getline(cin,T);
getNext(T);
for(int i=0; i<T.length(); i++) {
cout<<ne[i]<<" ";
}
return 0;
}
/*
input: ababaaababaa
output: -1 0 0 1 2 3 1 1 2 3 4 5
*/(2)严蔚敏定义法next数组值的算法代码
#include<iostream>
using namespace std;
const int maxn=100;
int ne[maxn];
void getNext(string s) {
int len=s.length();
int i=0, j=-1;
ne[0]=-1;
while(i<len) {
if(j==-1 || s[i]==s[j]) {
ne[++i]=++j;
} else j=ne[j];
}
}
int main() {
string T;
getline(cin,T);
getNext(T);
for(int i=0; i<T.length(); i++) {
cout<<ne[i]+1<<" ";
}
return 0;
}
/*
input: ababaaababaa
output: 0 1 1 2 3 4 2 2 3 4 5 6
*/● 通过观察,发现“李春葆、严蔚敏关于 KMP 算法的 next 数组值差 1”。这就给出了启发。即:
如果李春葆定义法的 next 数组值(以“-1 0 ”开头),利用 cout<<next[i]; 输出。
那么严蔚敏定义法的 next 数组值(以“0 1”开头),便可利用 cout<<next[i]+1; 输出。
也就是说,仅需修改一条语句,便可复用代码,实现李春葆定义法、严蔚敏定义法中 next 数组值的输出。
(三)KMP 算法中的 nextval 数组:https://blog.csdn.net/hnjzsyjyj/article/details/127105603
● 正是由于 next 数组的引入,使得 KMP 算法的效率大大优于 BF 算法。但是,next 数组在某些情况下仍存在缺陷。例如,针对模式串"aaaab",其相应的 next 数组值为“-1 0 1 2 3”。则据 next 数组的作用易知,当 T[3]=a 与主串 S[pos] 失配时,则会使用 T[next[3]]=T[2]=a 与主串 S[pos] 再进行匹配,显然还会失配。这是因为,T[0]~T[2] 与 T[3] 都相等,当 T[3] 与 S[pos] 失配时,T[0]~T[2] 与 S[pos] 必然也失配。显然 T[0]~T[2] 与 S[pos] 的比较没有意义,一定会匹配失败。针对本模式串"aaaab"而言,将会有 T[3]=a≠S[pos],T[next[3]]=T[2]=a≠S[pos],T[next[2]]=T[1]=a≠S[pos],T[next[1]]=T[0]=a≠S[pos] 等四次比较。
● nextval 数组的引入,正是为了减少这种无意义的比对,而对 next 数组进行的优化。
● 手动求 nextval 数组(模式串下标从 1 开始)
若在 KMP 算法设计中,将模式串下标从 1 开始计数,那么求 nextval 数组的算法步骤为:
(1)求出 next 数组的值(定义 next[1]=0,next[2]=1);
(2)定义 nextval[1]=0。然后,比较模式串的第 j 个(j>1)字符是否与第 next[j] 个字符相等。若相等,则模式串第 j 个字符的 nextval 值等于第 next[j] 个字符的 nextval 值。若不等,则模式串第 j 个字符的 nextval 值等于其 next 数组值。
即,若 T[j]=T[next[j]],则 nextval[j]=nextval[next[j]]。否则,nextval[j]=next[j]。
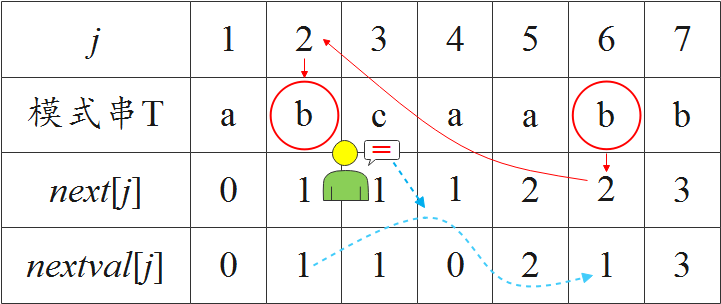

● 手动求 nextval 数组(模式串下标从 0 开始)
若在 KMP 算法设计中,将模式串下标从 0 开始计数,那么求 nextval 数组的算法步骤为:
(1)求出 next 数组的值(定义 next[0]=-1,next[1]=0);
(2)定义 nextval[0]=-1。然后,比较模式串的第 j 个(j>0)字符是否与第 next[j] 个字符相等。若相等,则模式串第 j 个字符的 nextval 值等于第 next[j] 个字符的 nextval 值。若不等,则模式串第 j 个字符的 nextval 值等于其 next 数组值。
即,若 T[j]=T[next[j]],则 nextval[j]=nextval[next[j]]。否则,nextval[j]=next[j]。
● 求 nextval 数组的算法代码
#include<iostream>
using namespace std;
const int maxn=100;
int ne[maxn],nev[maxn];
void getNext(string s) {
int len=s.length();
int i=0,j=-1;
ne[0]=-1;
while(i<len) {
if(j==-1||s[i]==s[j]) {
i++;
j++;
ne[i]=j;
} else j=ne[j];
}
}
void getNextval(string s) {
int len=s.length();
int i=0,j=-1;
nev[0]=-1;
while(i<len) {
if(j==-1||s[i]==s[j]) {
i++;
j++;
nev[i]=j;
if(s[i]!=s[j]) nev[i]=j;
else nev[i]=nev[j];
} else j=nev[j];
}
}
int main() {
string T;
getline(cin,T);
getNext(T);
for(int i=0; i<T.length(); i++) {
cout<<ne[i]<<" ";
}
cout<<endl;
getNextval(T);
for(int i=0; i<T.length(); i++) {
cout<<nev[i]<<" ";
}
return 0;
}
/*
input:
abcaabbabcab
output:
-1 0 0 0 1 1 2 0 1 2 3 4
-1 0 0 -1 1 0 2 -1 0 0 -1 4
*/
(四)KMP 算法模板代码:https://blog.csdn.net/hnjzsyjyj/article/details/127112363
#include<iostream>
using namespace std;
const int maxn=100;
int ne[maxn];
void getNext(string s) {
int len=s.length();
int i=0, j=-1;
ne[0]=-1;
while(i<len) {
if(j==-1 || s[i]==s[j]) {
i++;
j++;
ne[i]=j;
} else j=ne[j];
}
}
int KMP(string S,string T) {
int lens=S.length();
int lent=T.length();
int i=0;
int j=0;
while(i<lens && j<lent) {
if(j==-1 || S[i]==T[j]) {
i++;
j++;
} else j=ne[j];
}
if(j==lent) return i-j+1;
else return -1;
}
int main() {
string S,T;
getline(cin,S);
getline(cin,T);
getNext(T);
cout<<KMP(S,T)<<endl;
return 0;
}
/*
input:
i love china.
e c
output:
6
*/未来,很多与 KMP 算法相关的题目的代码,都可在这个模板代码上进行微调可得。
(五)KMP 算法应用实例:https://blog.csdn.net/hnjzsyjyj/article/details/127140892
HDU 2087:剪花布条:http://acm.hdu.edu.cn/showproblem.php?pid=2087
微调 KMP 算法模板代码,可得 ”HDU 2087:剪花布条”问题的代码。
#include<iostream>
using namespace std;
const int maxn=1010;
int ne[maxn];
void getNext(string s) {
int len=s.length();
int i=0, j=-1;
ne[0]=-1;
while(i<len) {
if(j==-1 || s[i]==s[j]) {
i++;
j++;
ne[i]=j;
} else j=ne[j];
}
}
int KMP(string S,string T) {
int lens=S.length();
int lent=T.length();
int i=0;
int j=0;
int cnt=0;
while(i<lens && j<lent) {
if(j==-1 || S[i]==T[j]) {
i++;
j++;
} else j=ne[j];
if(j==lent) {
cnt++;
j=0;
}
}
return cnt;
}
int main() {
string S,T;
while(cin>>S && S[0]!='#') {
cin>>T;
getNext(T);
cout<<KMP(S,T)<<endl;
}
return 0;
}
/*
input:
abcde a3
aaaaaa aa
output:
0
3
*/
【参考文献】
https://blog.csdn.net/hnjzsyjyj/article/details/127112363
https://blog.csdn.net/hnjzsyjyj/article/details/127086502
https://blog.csdn.net/hnjzsyjyj/article/details/127105603
https://blog.csdn.net/hnjzsyjyj/article/details/127114683