前言

现在面试越来越难，基本上是造火箭，而算法又是必不可少的面试题，对程序员来说，算法的要求也越来越高，如果没有好的算法基础，想进一家不错的公司基本上是无缘了，所以在此再回顾一下吧，把扔给老师的再补回来（T T）

算法的时间复杂度分析

定义：

在进行算法分析时，语句总的执行次数T(n)是关于问题规模n的函数，进而分析T(n)随着n的变化情况并确定T(n)的量级。

算法的时间复杂度，就是算法的时间量度，记作:T(n)=O(f(n))。它表示随着问题规模n的增大，算法执行时间的增长率和f(n)的增长率相同，称作算法的渐近时间复杂度，简称时间复杂度，其中f(n)是问题规模n的某个函数。

在这里，需要明确一个事情：

执行次数=执行时间

用大写O()来体现算法时间复杂度的记法，我们称之为大O记法。一般情况下，随着输入规模n的增大，T(n)增长最慢的算法为最优算法。

下面使用大O表示法来表示一些求和算法的时间复杂度：

算法一：

public static void main(String[] args) {
    int sum = 0;       //执行1次
    int n=100;         //执行1次
    sum = (n+1)*n/2;   //执行1次
    System.out.println("sum="+sum);
}

算法二：

public static void main(String[] args) {
    int sum = 0;      //执行1次
    int n=100;        //执行1次
    for (int i = 1; i <= n; i++) {
        sum += i;     //执行了n次
    }
    System.out.println("sum=" + sum);
}

算法三：

public static void main(String[] args) {
    int sum=0;//执行1次
    int n=100;//执行1次
    for (int i = 1; i <=n ; i++) {
        for (int j = 1; j <=n ; j++) {
            sum+=i;//执行n^2次
        }
    }
    System.out.println("sum="+sum);
}

如果忽略判断条件的执行次数和输出语句的执行次数，那么当输入规模为n时，以上算法执行的次数分别为：

• 算法一：3次

• 算法二：n+2次

• 算法三：n^2+2次

基于我们对函数渐近增长的分析，推导大O阶
的表示法有以下几个规则可以使用：

1.用常数1取代运行时间中的所有加法常数；

2.在修改后的运行次数中，只保留高阶项；

3.如果最高阶项存在，且常数因子不为1，则去除与这个项相乘的常数；

所以，上述算法的大O记法分别为：

• 算法一：O(1)

• 算法二：O(n)

• 算法三：O(n^2)

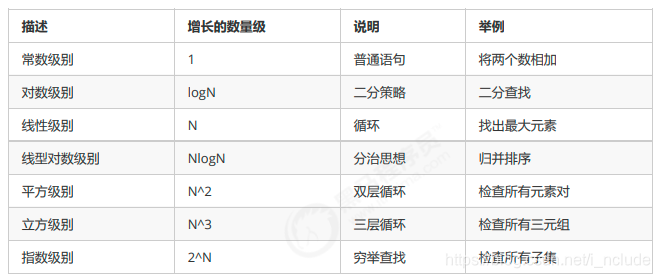
常见的大O阶

1.线性阶

public static void main(String[] args) {
    int sum = 0;
    int n=100;
    for (int i = 1; i <= n; i++) {
        sum += i;
    }
    System.out.println("sum=" + sum);
}

上面这段代码，它的循环的时间复杂度为O(n),因为循环体中的代码需要执行n次

2.平方阶

public static void main(String[] args) {
    int sum=0,n=100;
    for (int i = 1; i <=n ; i++) {
        for (int j = 1; j <=n ; j++) {
            sum+=i;
        }
    }
    System.out.println(sum);
}

上面这段代码，n=100，也就是说，外层循环每执行一次，内层循环就执行100次，那总共程序想要从这两个循环
中出来，就需要执行100*100次，也就是n的平方次，所以这段代码的时间复杂度是O(n^2).

3.立方阶

public static void main(String[] args) {
    int x=0,n=100;
    for (int i = 1; i <=n ; i++) {
        for (int j = i; j <=n ; j++) {
            for (int j = i; j <=n ; j++) {
                x++;
            }
        }
    }
    System.out.println(x);
}

上面这段代码，n=100，也就是说，外层循环每执行一次，中间循环循环就执行100次，中间循环每执行一次，最内层循环需要执行100次，那总共程序想要从这三个循环中出来，就需要执行100 * 100 * 100次，也就是n的立方，所以这段代码的时间复杂度是O(n^3).

4.对数阶

int i=1,n=100;

    while(i<n){
    
        i = i * 2;
        
    }

由于每次i*2之后，就距离n更近一步，假设有x个2相乘后大于n，则会退出循环。由于是2^x=n,得到x=log(2)n,所以这个循环的时间复杂度为O(logn);

5.线性对数阶

for(m=1; m<n; m++)
{
    i = 1;
    while(i<n)
    {
        i = i * 2;
    }
}

外层循环n次，每循环一次，里面的while循环都会执行log(2)n次，所以这个循环的时间复杂度为O(nlogn)

6.常数阶

public static void main(String[] args) {
    int n=100;
    int i=n+2;
    System.out.println(i);
}

上述代码，不管输入规模n是多少，都执行2次，根据大O推导法则，常数用1来替换，所以上述代码的时间复杂度
为O(1)

下面是对常见时间复杂度的一个总结：
他们的复杂程度从低到高依次为：

Ο(1)＜Ο(log2n)＜Ο(n)＜Ο(nlog2n)＜Ο(n2)＜Ο(n3)＜…＜Ο(2n)＜Ο(n!)

根据前面的折线图分析，我们会发现，从平方阶开始，随着输入规模的增大，时间成本会急剧增大，所以，我们的算法，尽可能的追求的是O(1),O(logn),O(n),O(nlogn)这几种时间复杂度，而如果发现算法的时间复杂度为平方阶、立方阶或者更复杂的，那我们可以分为这种算法是不可取的，需要优化。

最坏情况

从心理学角度讲，每个人对发生的事情都会有一个预期，比如看到半杯水，有人会说：哇哦，还有半杯水哦！但也
有人会说：天哪，只有半杯水了。一般人处于一种对未来失败的担忧，而在预期的时候趋向做最坏的打算，这样即
使最糟糕的结果出现，当事人也有了心理准备，比较容易接受结果。假如最糟糕的结果并没有出现，当事人会很快
乐。

算法分析也是类似，假如有一个需求：
有一个存储了n个随机数字的数组，请从中查找出指定的数字。

public int search(int num){
    int[] arr={11,10,8,9,7,22,23,0};
    for (int i = 0; i < arr.length; i++) {
        if (num==arr[i]){
            return i;
        }
    }
    return -1;
}

最好情况：

假如我们找的数字是11，查找的第一个数字就是期望的数字，那么算法的时间复杂度为O(1)

最坏情况：

假如查找的最后一个数字0，才是期望的数字，那么算法的时间复杂度为O(n)

平均情况：

任何数字查找的平均成本是O(n/2)

最坏情况是一种保证，在应用中，这是一种最基本的保障，即使在最坏情况下，也能够正常提供服务，所以，除非特别指定，我们提到的运行时间都指的是最坏情况下的运行时间。

算法的空间复杂度分析

计算机的软硬件都经历了一个比较漫长的演变史，作为为运算提供环境的内存，更是如此，从早些时候的512k,经
历了1M，2M，4M…等，发展到现在的8G，甚至16G和32G，所以早期，算法在运行过程中对内存的占用情况也是
一个经常需要考虑的问题。我么可以用算法的空间复杂度来描述算法对内存的占用。

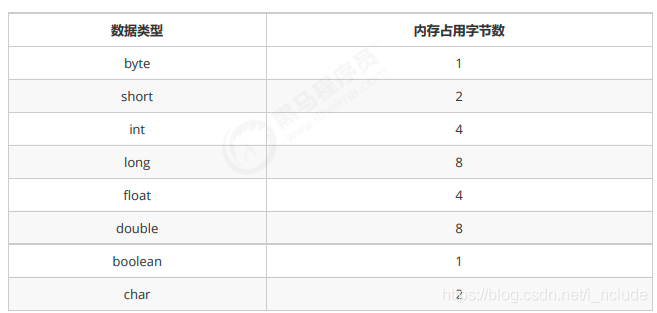
java中常见内存占用

1.基本数据类型内存占用情况：

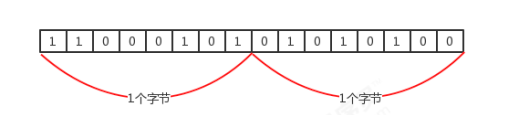
2.计算机访问内存的方式都是一次一个字节

3.一个引用（机器地址）需要8个字节表示：
例如：

Date date = new Date()

则date这个变量需要占用8个字节来表示

4.创建一个对象，比如

new Date()

除了Date对象内部存储的数据(例如年月日等信息)占用的内存，该对象本身也
有内存开销，每个对象的自身开销是16个字节，用来保存对象的头信息(JVM相关知识)。

5.一般内存的使用，如果不够8个字节，都会被自动填充为8字节：

public class Demo1{
    public int a  = 1;
}

通过new Demo1() 创建一个对象占用内存如下：

1.整型成员变量a占用4个字节

2.对象本身占用16个字节

那么创建该对象总共需要20个字节，但由于不是以8为单位，会自动填充为24个字节

6.java中数组被被限定为对象，他们一般都会因为记录长度而需要额外的内存，一个原始数据类型的数组一般需要
24字节的头信息(16个自己的对象开销，4字节用于保存长度以及4个填充字节)再加上保存值所需的内存。

算法的空间复杂度

了解了java的内存最基本的机制，就能够有效帮助我们估计大量程序的内存使用情况。
算法的空间复杂度计算公式记作：

S(n)=O(f(n))

其中n为输入规模，f(n)为语句关于n所占存储空间的函数。

对指定的数组元素进行反转，并返回反转的内容。

解法一：利用temp中间变量，直接把数组的第一个和最后一个交换位置，第二个和倒数第二个···

public static int[] reverse1(int[] arr){

int n=arr.length;//申请4个字节
int temp;//申请4个字节

for(int start=0,end=n-1;start<=end;start++,end--){
    temp=arr[start];
    arr[start]=arr[end];
    arr[end]=temp;
}
return arr;
}

解法二：创建一个新的数组，依次把原数组

public static int[] reverse2(int[] arr){
    int n=arr.length;       //申请4个字节
    int[] temp = new int[n];//申请n*4个字节+数组自身头信息开销24个字节
    for (int i = n-1; i >=0; i--) {
        temp[n-1-i]=arr[i];
    }
return temp;
}

忽略判断条件占用的内存，我们得出的内存占用情况如下：

算法一：
不管传入的数组大小为多少，始终额外申请4+4=8个字节；

算法二：
4+4n+24=4n+28;

根据大O推导法则，算法一的空间复杂度为O(1),算法二的空间复杂度为O(n),所以从空间占用的角度讲，算法一要优于算法二。

另外,如果觉得文章对你有用,下边点个赞吧!
你们的支持，是我坚持的动力。