前缀和&&差分目录
1. 前缀和的概念及作用
🌈概念
前缀和:
🎈对于一个给定的数列a,他的前缀和数中 s 中 s[ i ] 表示从第一个元素到第 i 个元素的总和。即s[ i ] = s[ i - 1 ] + a[ i ];
比如: s[ 1 ] = s[ 0 ] + a[ 1 ]。
注意:在使用前缀和和差分的时候,一般下标 0 不参与的运算,统一的将下表设置为从1开始,具体是要考虑到我们的边界问题,也就是S[1]的求法问题,为了保证我们循环的统一性,我们要将S[0]设置为0,所以我们索性就将下标从1开始设置起,这样也有利于我们后面的初始化。
🌈用途
可以用于一维前缀和和二维前缀和。
模板如下:
🌙一维前缀和
核心代码如下:
s[i] = s[i-1] + a[i]
s[i] = a[1] + a[2] + ... a[i]
a[l] + ... + a[r] = s[r] - s[l - 1]🧩例题如下:
题目练习: AcWing 795. 前缀和
思路:
首先做一个预处理,定义一个s数组,让s[ i ]代表 a 数组前 i 个数的和。
然后运用求一维前缀和运算的公式 s[i] = s[i-1] + a[i] 。
再进行查询操作:即s[ r ] - s[ l - 1] ,这样使得求 [ l, r ]的和的时间复杂度变为 O (1).
注意:求 [ l, r ]的和是s[ r ] - s[ l - 1],之所以要 l - 1是因为,a[ l ] 也包括在内
因为a[l] + ... + a[r] = s[r] - s[l - 1]
AC代码如下:
#include <iostream>
using namespace std;
const int N = 1e5+10;
int a[N], s[N];
int main(){
int n, m, x;
cin>>n>>m;
for(int i = 1; i <= n; i++) cin>>a[i];
for(int i = 1; i <= n; i++) s[i] = a[i] + s[i - 1];
int l, r;
while(m--){
cin>>l>>r;
cout<<s[r] - s[l - 1]<<endl;
}
return 0;
}🌙二维前缀和
和一维前缀和的原理类似,只不过二维前缀和求的是一个矩阵中所有元素的和。
如下图:
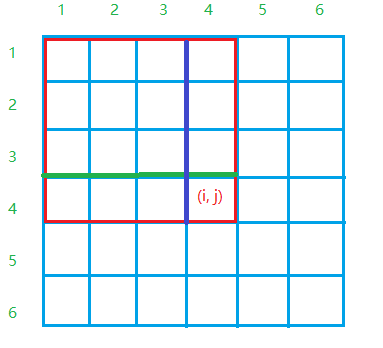
因此通过上面的图我们就可以更好理解下图来推导公式了:
s[ i ][ j ] 即为框内所有数的和:s[ i ][ j ]=s[ i ][ j - 1 ]+s[ i - 1 ][ j ] - s[ i - 1 ][ j - 1 ]+a[ i ][ j ];
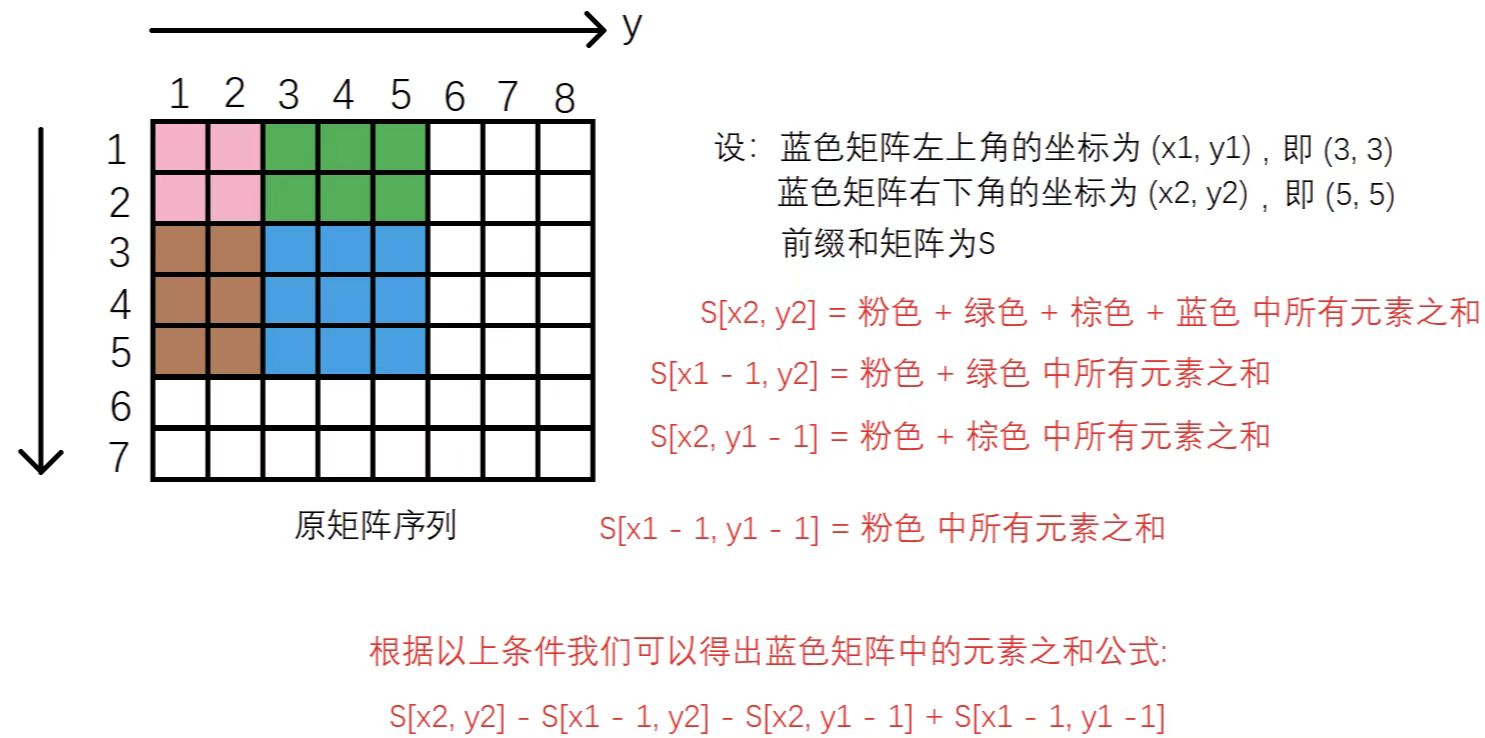
而(x1, y1) 到 (x2, y2)的矩阵大小为s[x2][y2]-s[x1-1][y2]-s[x2][y1-1]+s[x1-1][y1-1]
核心代码:
s[x][y]=s[x][y-1]+s[x-1][y]-s[x-1][y-1]+a[x][y];
s[x2][y2]-s[x1-1][y2]-s[x2][y1-1]+s[x1-1][y1-1]🧩例题如下:
题目练习: AcWing 796. 子矩阵的和
思路:
先做一个预处理,定义一个s矩阵,s[ i ][ j ]代表 a 矩阵前 从(0,0)到(i,j)的矩阵和。
然后运用求一维前缀和运算的公式 s[i] = s[i-1] + a[i] 。
再进行查询操作:即s[x2][y2]-s[x1-1][y2]-s[x2][y1-1]+s[x1-1][y1-1]。
这样使得求 (x1, y1) 到 (x2, y2)的矩阵大小的和的时间复杂度变为 O (1).
AC代码如下:
#include <iostream>
using namespace std;
const int N = 1005;
int a[N][N], s[N][N];
int main(){
int n, m, q;
cin >> n >> m >> q;
//第一步:输入矩阵的值
for (int i = 1; i <= n; i++){
for (int j = 1; j <= m; j++){
cin >> a[i][j];
}
}
//第二步:求矩阵前缀和
for (int i = 1; i <= n; i++){
for (int j = 1; j <= m; j++) {
s[i][j] = s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1] + a[i][j];
}
}
//第三步:查找(x1,y1)到(x2,y2)的矩阵大小
while (q--)
{
int x1, x2, y1, y2;
cin >> x1 >> y1 >> x2 >> y2;
printf("%d\n", s[x2][y2] - s[x2][y1 - 1] - s[x1 - 1][y2] + s[x1 - 1][y1 - 1]);
}
return 0;
}
2. 差分的概念及用途
🌈概念:
差分:
🎈 类似于数学中的求导和积分,差分可以看成前缀和的逆运算
对于一个给定的数列a,其中a[1],a[2]…a[n]作为前缀和。它的差分数组中 b 中 b[ i ] 表示从第 i - 1个元素到第 i 个元素的差值。即b[ i ] = a[ i ] - s[ i - 1 ];
一维差分数组的构造也很简单,即a[1] = b[1], b[2] = a[2] - a[1], b[n] = a[n] - a[n-1];
注意:刚开始时可以初始化数组a,b全部为0,输入a数组后;在构造时,只需要将b[1]看做在[1, 1]区间上加上a[1]; b[2] 看作在[2, 2]区间上加上a[2];
🌈用途
🌙一维差分
差分数组的好处是可以简化运算,例如想要给一个区间 [l,r] 上的数组加一个常数c,原始的方法是依次加上c,这样的时间复杂度是O(n)的。但是如果采用差分数组的话,可以大大降低时间复杂度到O(1)。
因此只需要将b[l] = b[l] + c 即可,这样l之后的数字会依次加上常数c,而在 b[r]处,将b[r+1] = b[r+1] - c ,这样r之后的数组又会恢复原值,仅需要处理这两个边界的差分数组即可。时间复杂度大大降低。
核心代码如下:
b[i]=a[i]-a[i-1];
a[i] = b[i] + a[i - 1];🧩例题如下:
题目练习: AcWing 797. 差分
思路:
首先做一个预处理,定义一个b数组,让b[ i ]代表a[ i ] - a[ i -1 ].
因此只需要将b[l] = b[l] + c 即可,这样l之后的数字会依次加上常数c,而在 b[r]处,将b[r+1] = b[r+1] - c ,这样r之后的数组又会恢复原值,仅需要处理这两个边界的差分数组即可。
AC代码如下:
#include <iostream>
using namespace std;
const int N = 1e5 + 5;
int b[N], a[N];
int main()
{
int n, m;
cin>>n>>m;
for (int i = 1; i <= n; i++){
scanf("%d", &a[i]);
b[i]=a[i]-a[i-1];
}
while(m--){
int l,r,c;
cin>>l>>r>>c;
b[l]+=c;
b[r+1]-=c;
}
for (int i = 1; i <= n; i++){
a[i] = b[i] + a[i - 1];
printf("%d ", a[i]);
}
return 0;
}🌙二维差分
如果扩展到二维,我们需要让二维数组被选中的子矩阵中的每个元素的值加上c,是否也可以达到O(1)的时间复杂度。答案是可以的,考虑二维差分。
a[][]数组是b[][]数组的前缀和数组,那么b[][]是a[][]的差分数组原数组:
a[i][j]我们去构造差分数组:
b[i][j]使得
a数组中a[i][j]是b数组左上角(1,1)到右下角(i,j)所包围矩形元素的和。
如何构造b数组呢?
其实关于差分数组,我们并不用考虑其构造方法,因为我们使用差分操作在对原数组进行修改的过程中,实际上就可以构造出差分数组。
同一维差分,我们构造二维差分数组目的是为了 让原二维数组a中所选中子矩阵中的每一个元素加上c的操作,可以由O(n*n)的时间复杂度优化成O(1)
已知原数组a中被选中的子矩阵为 以(x1,y1)为左上角,以(x2,y2)为右下角所围成的矩形区域;
始终要记得,a数组是b数组的前缀和数组,比如对b数组的b[i][j]的修改,会影响到a数组中从a[i][j]及往后的每一个数。
假定我们已经构造好了b数组,类比一维差分,我们执行以下操作
来使被选中的子矩阵中的每个元素的值加上c
b[x1][y1] + = c ;
b[x1,][y2+1] - = c;
b[x2+1][y1] - = c;
b[x2+1][y2+1] + = c;
每次对b数组执行以上操作,等价于:
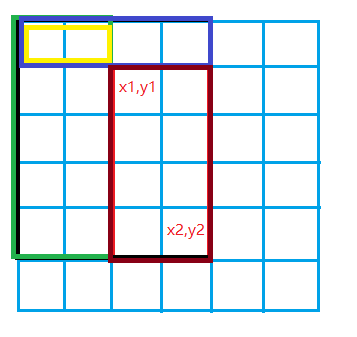
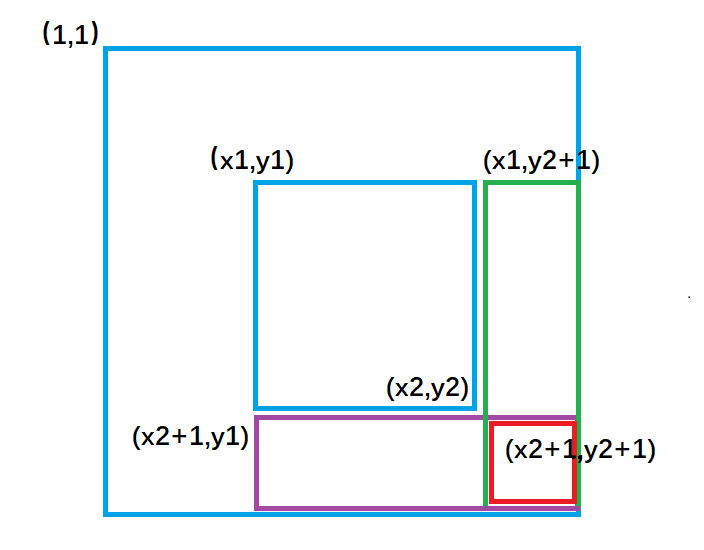
b[x1][y1] += c ; 对应图1 ,让整个a数组中蓝色矩形面积的元素都加上了c。
b[x1,][y2 + 1] -= c ; 对应图2 ,让整个a数组中绿色矩形面积的元素再减去c,使其内元素不发生改变。
b[x2 + 1][y1] -= c ; 对应图3 ,让整个a数组中紫色矩形面积的元素再减去c,使其内元素不发生改变。
b[x2 + 1][y2 + 1] += c; 对应图4,让整个a数组中红色矩形面积的元素再加上c,红色内的相当于被减了两次,再加上一次c,才能使其恢复。
核心代码如下:
b[i][j] = a[i][j] − a[i − 1][j] − a[i][j − 1] + a[i −1 ][j − 1]
b[x1][y1] += c;
b[x2 + 1][y1] -= c;
b[x1][y2 + 1] -= c;
b[x2 + 1][y2 + 1] += c;
题目练习: AcWing 798. 差分矩阵
AC代码如下:
#include <iostream>
using namespace std;
const int N = 1005;
int a[N][N], b[N][N];
int main(){
int n, m, q;
cin >> n >> m >> q;
for (int i = 1; i <= n; i++){
for (int j = 1; j <= m; j++) {
cin >> a[i][j];
b[i][j] = a[i][j] - a[i - 1][j] - a[i][j - 1] + a[i - 1][j - 1];
}
}
while (q--){
int x1, x2, y1, y2, c;
cin >> x1 >> y1 >> x2 >> y2 >> c;
b[x1][y1] += c, b[x2 + 1][y2 + 1] += c;
b[x1][y2 + 1] -= c, b[x2 + 1][y1] -= c;
}
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
a[i][j] = a[i - 1][j] + a[i][j - 1] - a[i - 1][j - 1] + b[i][j];
cout << a[i][j] << " ";
}
cout << endl;
}
return 0;
}