算法的重要性,我就不多说了吧,想去大厂,就必须要经过基础知识和业务逻辑面试+算法面试。所以,为了提高大家的算法能力,这个公众号后续每天带大家做一道算法题,题目就从LeetCode上面选 !
今天和大家聊的问题叫做 数组中两个数的最大异或值,我们先来看题面:
https://leetcode-cn.com/problems/maximum-xor-of-two-numbers-in-an-array/
Given an integer array nums, return the maximum result of nums[i] XOR nums[j], where 0 <= i <= j < n.
给你一个整数数组 nums ,返回 nums[i] XOR nums[j] 的最大运算结果,其中 0 ≤ i ≤ j < n 。
进阶:你可以在 O(n) 的时间解决这个问题吗?
示例
示例 1:
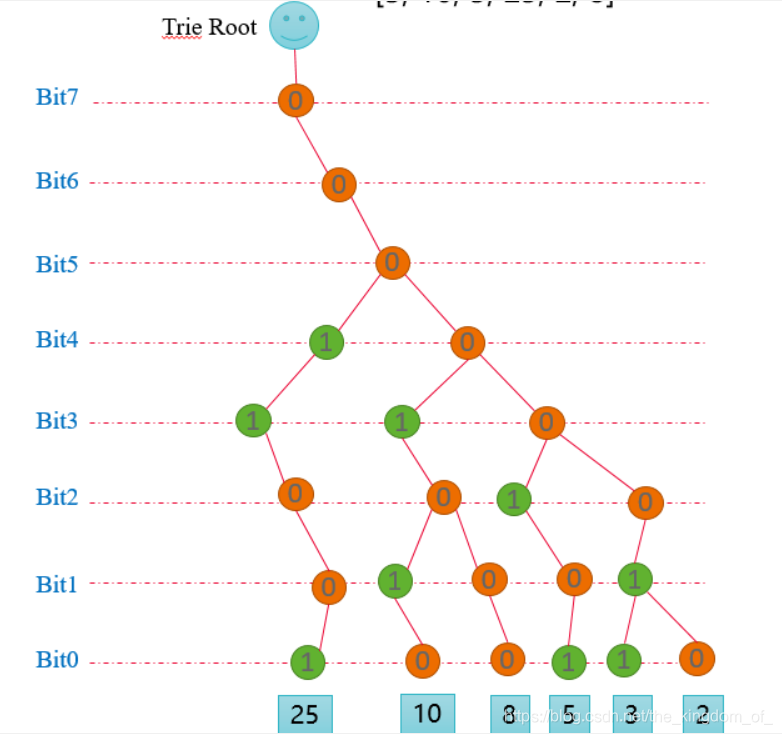
输入:nums = [3,10,5,25,2,8]
输出:28
解释:最大运算结果是 5 XOR 25 = 28.
示例 2:
输入:nums = [0]
输出:0
示例 3:
输入:nums = [2,4]
输出:6
示例 4:
输入:nums = [8,10,2]
输出:10
示例 5:
输入:nums = [14,70,53,83,49,91,36,80,92,51,66,70]
输出:127解题
https://blog.csdn.net/the_kingdom_of_/article/details/107988384
【Trie树】Trie树建立的思路,整数在存储时需要32bit,因此可以把整数看作为含有32字符的字符串,其中每个字符为0或1,则可以使用二叉树构建前缀树。从高位到低位进行构建,其中左结点为1,右结点为0.
【位运算找最大异或值】如何找到最大值异或,两个数异或得到一个尽可能大的数,则第一个1出现的位数越高则数越大,所以可以从最高位开始,找和它相反的数,如果存在这这个数异或即得到最大异或值,若不存在则,则继续相下找,直到找到相异的位。
class Solution {
struct TreeNode{
int val;
TreeNode* left;
TreeNode* right;
TreeNode(int _val): val(_val), left(nullptr), right(nullptr) {}
};
public:
int findMaximumXOR(vector<int>& nums) {
//字典和建树都需要用到贪心算法
//建树 0->left 1->right
TreeNode root(-1);
int max = 0;
//先进行建树
for(auto num : nums){
TreeNode* ptr = &root;
for(int i = 31; i >= 0; i--){
if(num & (0x1 << i)){
if(ptr->right == nullptr){
ptr->right = new TreeNode(1);
}
ptr = ptr->right;
}else{
if(ptr->left == nullptr){
ptr->left = new TreeNode(0);
}
ptr = ptr->left;
}
}
ptr->left = new TreeNode(num);
}
//应用贪心算法,查找当前num下能产生最大异或值得组合
for(auto num : nums){
TreeNode* ptr = &root;
for(int i = 31; i >=0; i--){
if(num & (0x1 << i)){ //当前位是1,则必须查找该位为0的如果没有就走1的路
if(ptr->left){
ptr = ptr->left;
}else{
ptr = ptr->right;
}
}else{
if(ptr->right){
ptr = ptr->right;
}else{
ptr = ptr->left;
}
}
}
if((num^(ptr->left->val)) > max){
max = (num^(ptr->left->val));
}
}
return max;
}
};好了,今天的文章就到这里,如果觉得有所收获,请顺手点个在看或者转发吧,你们的支持是我最大的动力 。
上期推文: