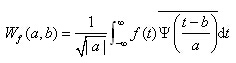题目:连续小波变换、离散小波变换、二进小波变换、离散序列的小波变换、小波包
初学小波者尤其是有数字信号处理基础的初学者,很容易拿傅里叶变换与小波变换对比着学习,但容易造成越比越混乱的现象,比如Matlab里fft函数所做的事就是离散傅里叶变换DFT,但Matlab里的dwt函数所做的事可不是离散小波变换的定义式,对于不想深入了解只想做应用的人来讲,真心挺乱的,“我只是想用一下小波变换而已,就像用傅里叶变换一样,至于么?”,其实就是因为一些概念没区分清楚。
一、连续小波变换(Continuous Wavelet Transform, CWT)
只要学习小波,第一个见到的应该就是连续小波变换了,这个也好理解,公式如下:
这就是信号f(t)的连续小波变换公式,其中参数a和b都是连续变化的参数,a为尺度参数(在某种意义上就是频率的概念),b是时间参数或平移参数。不严谨地讲,Wf(a,b)指的是对信号f(t)进行小波变换后当频率为a时间为b时的变换值。可以看出,一维信号f(t)经过小波变换后将变成二维信号。
二、离散小波变换(Discrete Wavelet Transform, DWT)
我们关注离散小波变换多数情况实际上是得到一个类似于离散傅里叶变换DFT的变换,时域和变换域都是离散有限长的,方便计算机处理。然而,DWT指的是将CWT中的尺度参数a和平移参数b离散化。这里要特别注意:DWT并没有将信号f(t)和小波ψ(t)中的时间变量t离散化!这与DFT的概念是非常不一样的!!
在尺度参数a和平移参数b离散过程中,一般对尺度进行幂数级离散化,即令a=a0m,对b均匀离散,考虑到不同尺度下频率不同,因此不同尺度下参数b的离散间隔不同。
三、二进小波变换(Dyadic Wavelet Transform)
前面提到,离散小波变换是对尺度参数a和平移参数b都进行了离散化,一般对尺度进行幂数级离散化,即令a=a0m,若特殊化取a0=2,然后保持平移参数b仍是连续的,则这类小波我们称为二进小波变换。总结起来,二进小波变换的概念介于CWT和DWT之间:相比于CWT,二进小波变换的尺度参数是特殊离散化的(a=2m);相比于DWT,二进小波变换的尺度参数不能随意离散,而是特殊离散化的(a=2m),平移参数b是保持连续变化。
四、离散序列的小波变换
实际上,很多时候我们绕一大圈是为了研究离散序列的小波变换,即类似于DFT的小波变换。要彻底说明白离散序列的小波变换,这就涉及到多分辨率分析(Multi-ResolutionAnalysis, MRA)、尺度函数、二尺度方程等概念,这就比较麻烦了,我也讲不太好,有兴趣可以看一下几篇网络博客(建议自行搜索,原链接已不存在@20200814):小波分析和尺度函数(上篇、中篇、下篇)、小波变换和motion信号处理(二)。
到这里有必要提一下正交小波变换,前面说了三种小波变换,但它们的小波基都不是正交的,这会带来一些麻烦,通过它们对信号变换后的信息是有冗余的,因此构建正交小波基是有重要意义的。Mallat给出了一种在正交小波基上的信号分解算法,也就是著明的Mallat算法了。
离散序列的小波变换就是基于著明的Mallat算法,实际上Mallat算法也是针对连续信号的,但在每一层的分解过程中(这里说的每一层实际上就是前面尺度的概念),各层分解系数之间有着某种关系,什么关系呢?那就看看Mallat算法框图吧,如下图所示:
初始系数x(暂且这么称呼)与其第一层分解后的高频系数D1(细节部分Detail)的关系是x经过高通滤波器g滤波后再下采样,与低频系数A1(近似部分Approximate)的关系是x经过低通滤波器h滤波后再下采样;然后继续对低频系数A1进行第二层分解,低频系数A1与其第二层分解后的高频系数D2(细节部分Detail)的关系是A1经过高通滤波器g滤波后再下采样,与低频系数A1(近似部分Approximate)的关系是A1经过低通滤波器h滤波后再下采样;后面依次类推即可。由于一直在下采样,所以虽然滤波器系数g和h不变,但其滤波带宽一直在减半。初始系数是怎么来的呢?肯定是根据信号得到的,最简单最粗糙的办法就是对信号直接抽样。这是对连续信号进行正交小波分解,有了这些系数,再利用正交小波基,就可以表示出信号了,这类似于连续周期信号的傅里叶级数分解吧。
从Matllat算法的框图可以看出,从始至终这是对离散序列x再进行变换分解,即初始系数即是离散信号x,经过多层分解后最后各分解系数合起来就是变换的结果。Matlab中的dwt函数可以实现单层分解,相关内容可参见《压缩感知稀疏基之离散小波变换》。
五、小波包(Wavelet Packet)
细心的人可能会问,在Mallat算法中为什么只对低频系数继续进行分解呢?是的,这在很多时候并不是最恰当的分解方式,有的时候对高频系数进行分解更合适,有的时候对低频系数进行分解更合适,这要取决于信号的特点。
小波包的概念大概就是这样子:无论是低频系数还是高频系统都进行同样的分解,然后选取一个最合适的分解路径。怎么评价分解是否是最优的呢?最自然的想法就是利益最大化或者是代价最小化,构建一个代价函数求一下看看如分解代价最小。代价函数有很多种,具体不说了。
参考文献:
【1】魏明果.实用小波分析[M].北京:北京理工大学出版社,2005.
【2】葛哲学,沙威.小波分析理分与MATLAB R2007实现[M].北京:电子工业出版社,2007.
【3】董长虹. Matlab小波分析工具箱原理与应用[M].北京:国防工业出版社,2004.