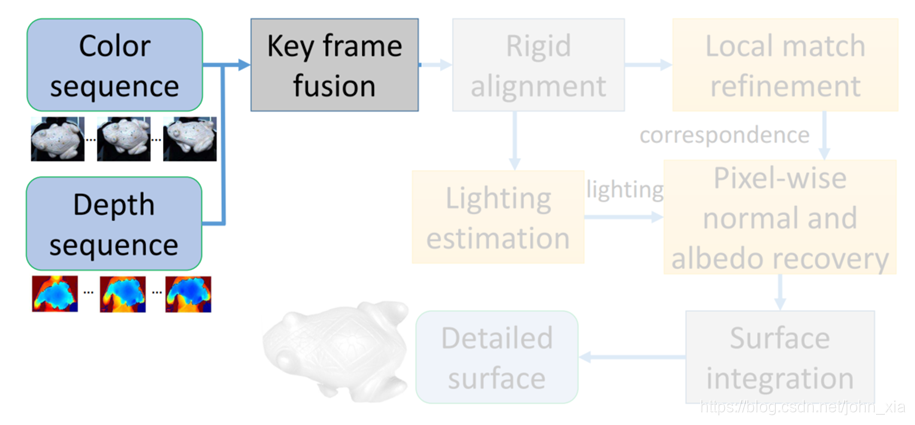
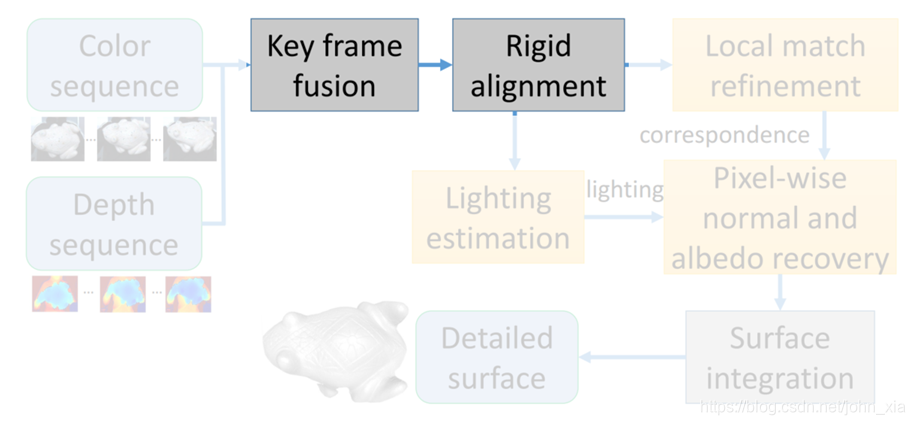
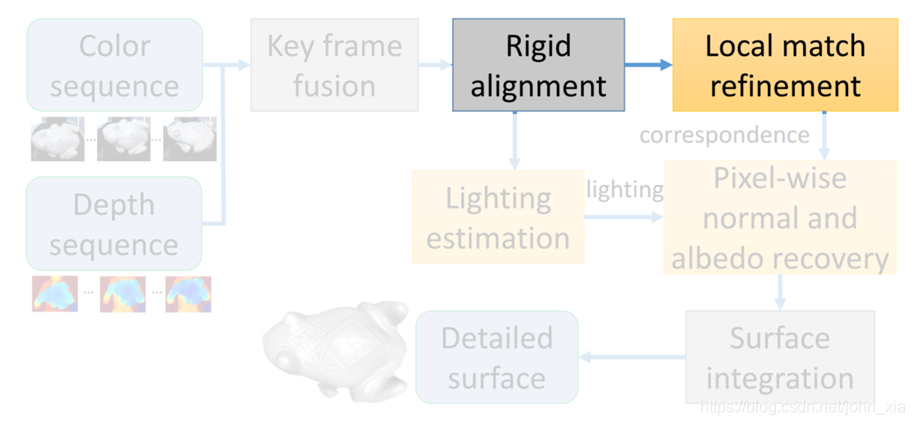
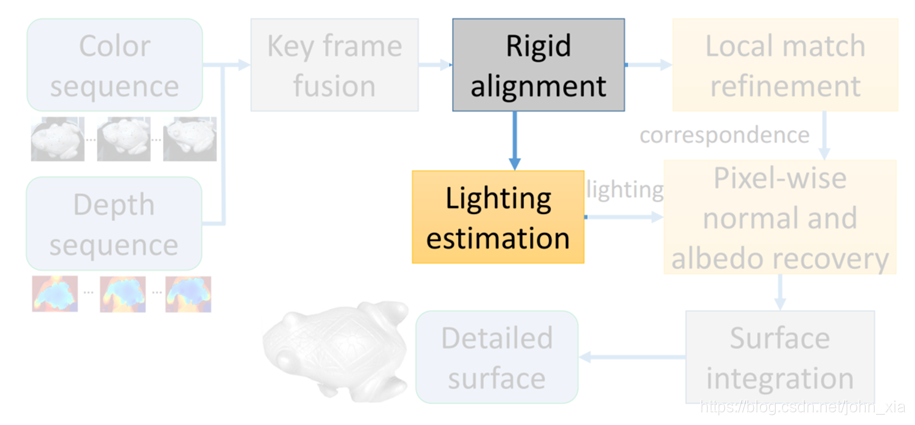
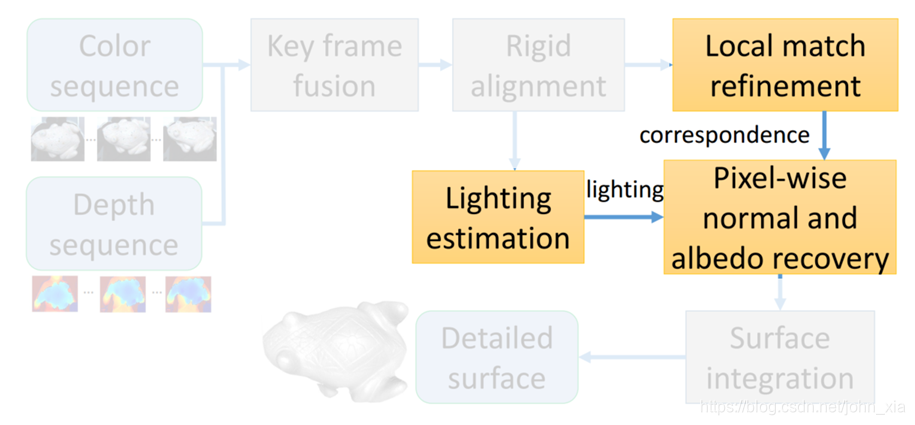
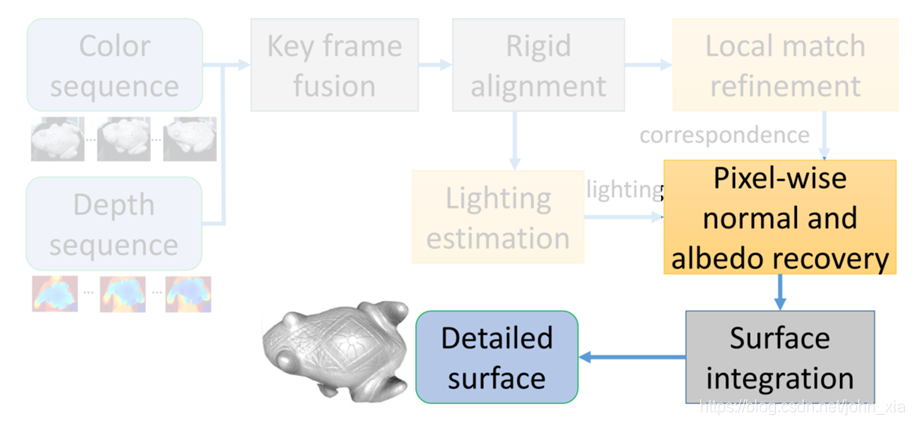
【paper reading】Detailed Surface Geometry and Albedo Recovery from RGB-D Video Under Natural Illumination
论文名字太长,标题写不全,有点尴尬。这篇论文是百度的杨睿刚老师之前在ICCV’ 17上的工作。
1.简介
论文中使用二代kinect,把相机固定在一个位置上,然后物体在自然环境照明下在画面内运动,最后拍摄物体运动的RGB-D图像序列。通过RGB-D图像序列来恢复精细的物体三维形状。整个方法对于物体的运动以及照明情况没有什么先验的要求,但是它要求物体是漫反射的。
2.具体方法
2.1 RGB-D数据预处理
论文中的做法其实很好理解。为了初始数据更加稳定,去除一些噪声,首先对于拍下的视频序列,将每20帧RGB-D图像融合成一个更加精细的深度图和与这个深度图相对应的RGB图像,就相当于关键帧。知道了每个视角下的深度图,就能融合成一个完整的三维模型,并且标定出相机的位姿。
2.2 图像间像素匹配
在论文里需要对像素点进行追踪,记录不同RGB图像中同一像素在不同的位置和方向下的RGB变化,这就需要对不同图像中的像素找它们的对应关系。之前已经计算出了每个视图下的相机位姿并且有物体的三维形状,最简单的就是将二维点恢复到三维表面上,再投影到另一幅图像上。
λ
[
q
1
]
=
K
(
R
k
(
K
−
1
∗
[
u
v
D
r
e
f
(
u
,
v
)
]
)
+
T
k
)
\lambda \left[\begin{matrix} q \\ 1 \end{matrix}\right] = K \bigg(R_k(K^{-1}* \left[\begin{matrix} u \\ v \\ D_{ref}(u,v)\end{matrix}\right])+T_k \bigg)
λ[q1]=K(Rk(K−1∗⎣⎡uvDref(u,v)⎦⎤)+Tk)
从而找到参考图像
I
r
e
f
I_{ref}
Iref中的像素
p
=
(
u
,
v
)
p = (u,v)
p=(u,v)在其他图像
I
k
I_k
Ik中的对应像素
q
q
q,其中
R
k
R_k
Rk和
T
k
T_k
Tk是第k幅图像的相机参数,
K
K
K是整个序列中的RGB相机的内参矩阵,
D
r
e
f
(
u
,
v
)
D_{ref}(u,v)
Dref(u,v)是参考图像中像素点
p
=
(
u
,
v
)
p = (u,v)
p=(u,v)的深度值。
然而这里相机的位姿以及物体表面都是有误差的,最后产生的对齐是有很大偏移的,但是算法的要求是找到像素之间的对应关系,因此就要求起码像素精度的匹配,这显然是不行的,起码不能直接这样用。之后他们也试过光流的方法进行匹配,但是因为物体是运动的,表面的明暗在不同图像中是不一样的,因此效果也不好,最后他们自己设计了一套对光照稳健的鲁棒匹配方法。
在SfSNet那篇中简单介绍了一下二阶球谐光照模型。光照可以用3*3的矩阵来表示,一般方法中把光照对特定方向 n \mathbf n n的平面的影响,即shading function表示成 s ( n ) = n T A n s(\mathbf n) = \mathbf n^TA\mathbf n s(n)=nTAn。但是在本论文中,作者将shading function表示成 s ( n ) = n T A n + b T n + c s(\mathbf n) = \mathbf n^TA\mathbf n+b^T\mathbf n+c s(n)=nTAn+bTn+c。其实大同小异。最后图像中p点的像素值就是shading function与表面点的原始反照率作用的结果,即 I ( p ) = ρ ( p ) ⋅ s ( n ( p ) ) I(p)=\rho(p)\cdot s(\mathbf n(p)) I(p)=ρ(p)⋅s(n(p))。
shading function的值作者当作常数处理,即隐含着一个先验,就是光照对RGB三个通道作用是一样的,即隐性的假设了光是白色的光。在这种假设下,不管物体如何运动,表面法向如何改变,只改变s这个系数,而RGB三个分量的比率,即色调都是不变的,因此论文中将每个颜色通道都除以三个通道亮度值的和,最后得到一个光度归一化后的图像,来抵抗变化光照带来的影响。
I
c
h
c
n
(
p
)
=
I
c
h
(
p
)
I
R
(
p
)
+
I
G
(
p
)
+
I
B
(
p
)
c
h
∈
{
R
,
G
,
B
}
I_{ch}^{cn}(p)=\frac{I_{ch}(p)}{I_R(p)+I_G(p)+I_B(p)}\ \ \ \ \ \ \ ch\in \left\{R,G,B \right\}
Ichcn(p)=IR(p)+IG(p)+IB(p)Ich(p) ch∈{R,G,B}
之前通过三维信息进行的匹配虽然粗糙不满足要求,但是大体还是正确的,因此作者就用第一帧,记作参考帧上的点与其他帧上对应点的小范围邻域内进行归一化互相关计算(NCC),找和参考帧上的点相关系数最大点。要求互相关系数要大于0.75,并且最高分要比次高分高至少0.05,这类似于SIFT特征点的匹配策略。因此不是所有点都能找到它的对应点。那些找到了对应的点称为控制点,直接计算他们在图像上的坐标位移,非控制点就通过最近邻的控制点的位移进行插值。最终的匹配对齐效果如下:
这里其实我觉得有点问题,在整个乌龟表面的色调都是灰色的,虽然进行光度归一化后消除了高光阴影等因素的影响,但是也可能使得一些纹理细节更难以分辨。可以看到实验中在乌龟上贴了一些贴纸,除了测试算法对于反照率突变的稳定性,我觉得可能更是为了在表面添加标记点从而使得像素匹配更鲁棒。
2.3 光照估计
在有不同图像间像素匹配关系的前提下。在不同图像中,将对应像素点p和q的像素值的生成公式相除,因为它们是同一个三维点,因此反照率可以约去。
I
k
(
q
)
I
r
e
f
(
p
)
=
ρ
(
q
)
(
n
q
T
R
T
A
R
n
q
+
b
T
R
n
q
+
c
)
ρ
(
p
)
(
n
p
T
R
T
A
R
n
p
+
b
T
R
n
p
+
c
)
=
n
q
T
R
T
A
R
n
q
+
b
T
R
n
q
+
c
n
p
T
R
T
A
R
n
p
+
b
T
R
n
p
+
c
\frac{I_k(q)}{I_{ref}(p)}=\frac{\rho(q)(n_q^TR^TARn_q+b^TRn_q+c)}{\rho(p)(n_p^TR^TARn_p+b^TRn_p+c)}=\frac{n_q^TR^TARn_q+b^TRn_q+c}{n_p^TR^TARn_p+b^TRn_p+c}
Iref(p)Ik(q)=ρ(p)(npTRTARnp+bTRnp+c)ρ(q)(nqTRTARnq+bTRnq+c)=npTRTARnp+bTRnp+cnqTRTARnq+bTRnq+c
法向量n和相机的旋转矩阵R之前已经计算出了。最终等式中的未知数只有光照。每一个像素对应关系都能列3个等式,总共就只有11个未知数。计算光照可以使用全部参考图像中的像素点与图像序列中的直接使用最小二乘法就能算出来。论文中的做法是将光照估计使用下列的函数进行优化
a
r
g
min
A
,
b
,
c
∑
k
∑
p
∈
I
r
e
f
γ
p
∥
n
q
T
R
T
A
R
n
q
+
b
T
R
n
q
+
c
n
p
T
R
T
A
R
n
p
+
b
T
R
n
p
+
c
−
I
k
(
q
)
I
r
e
f
(
p
)
∥
2
\mathrm {arg} \min_{A,b,c}\sum_{k}\sum_{p \in I_{ref}}\gamma_p\lVert \frac{n_q^TR^TARn_q+b^TRn_q+c}{n_p^TR^TARn_p+b^TRn_p+c} - \frac{I_k(q)}{I_{ref}(p)}\rVert^2
argA,b,cmink∑p∈Iref∑γp∥npTRTARnp+bTRnp+cnqTRTARnq+bTRnq+c−Iref(p)Ik(q)∥2
前面的这个系数
γ
p
\gamma_p
γp是为了抵抗噪声和阴影的。
2.4 反照率与法向恢复
之后就是恢复每个像素的反照率和更精细的法向,这里作者利用了EM算法来进行计算,将它变成一个优化过程。优化的目标函数是,
E
(
n
,
ρ
∣
O
)
=
∑
k
∥
ρ
⋅
s
k
(
n
)
−
I
k
W
∥
2
,
E(\mathbf n,\rho|O)=\sum_{k}\lVert\rho\cdot s_k(\mathbf n)-I_k^W\rVert^2,
E(n,ρ∣O)=k∑∥ρ⋅sk(n)−IkW∥2,
s
k
(
n
)
=
n
T
R
k
T
A
R
k
n
+
b
T
R
k
n
+
c
s_k(\mathbf n)=\mathbf n^TR_k^TAR_k\mathbf n+b^TR_k\mathbf n+c
sk(n)=nTRkTARkn+bTRkn+c
其意义就是使得估计的反照率和法向生成的效果需要和拍摄的图像上的像素值尽可能一样。但是这里存在隐变量的干扰,即物体在图像中是否符合朗伯照明假设。如果在阴影中或者高光以及镜面反射这些情况,就不是朗伯照明。
(5月7号更新)所有的变量为
Ω
=
{
n
,
ρ
,
σ
,
α
}
\Omega = \{n,\rho,\sigma,\alpha\}
Ω={n,ρ,σ,α}。在这里所有的操作都是针对单个像素进行的,因此每个像素都有自己的一套变量
Ω
\Omega
Ω。目标就是最大化后验概率
P
(
O
k
∣
Ω
)
P(O_k|\Omega)
P(Ok∣Ω)
P
(
O
k
∣
Ω
)
=
α
⋅
1
2
π
σ
exp
(
−
∥
ρ
⋅
s
k
(
n
)
−
I
k
W
∥
2
2
σ
2
)
+
(
1
−
α
)
⋅
1
C
P(O_k|\Omega)=\alpha\cdot\frac{1}{\sqrt{2\pi}\sigma}\exp\big(-\frac{\parallel\rho\cdot s_k(n)-I_k^W\parallel^2}{2\sigma^2}\big)+(1-\alpha)\cdot\frac{1}{C}
P(Ok∣Ω)=α⋅2πσ1exp(−2σ2∥ρ⋅sk(n)−IkW∥2)+(1−α)⋅C1
前面半部分是符合朗伯模型的情况,后面半部分是不符合朗伯模型的情况,如果不符合则直接给一个
1
C
\frac{1}{C}
C1的惩罚。
P
(
H
k
=
1
)
=
α
P(H_k=1)=\alpha
P(Hk=1)=α是符合朗伯模型的概率。
在E步骤通过目前的反照率和法向推断符合朗伯照明假设的概率。
ω
k
=
P
(
H
k
=
1
∣
O
k
,
Ω
′
)
=
α
⋅
exp
(
−
∥
ρ
⋅
s
k
(
n
)
−
I
k
W
∥
2
2
σ
2
)
α
⋅
exp
(
−
∥
ρ
⋅
s
k
(
n
)
−
I
k
W
∥
2
2
σ
2
)
+
1
−
α
C
\omega_k=P(H_k=1|O_k,\Omega')=\frac{\alpha\cdot\exp\big(-\frac{\parallel\rho\cdot s_k(n)-I_k^W\parallel^2}{2\sigma^2}\big)}{\alpha\cdot\exp\big(-\frac{\parallel\rho\cdot s_k(n)-I_k^W\parallel^2}{2\sigma^2}\big)+\frac{1-\alpha}{C}}
ωk=P(Hk=1∣Ok,Ω′)=α⋅exp(−2σ2∥ρ⋅sk(n)−IkW∥2)+C1−αα⋅exp(−2σ2∥ρ⋅sk(n)−IkW∥2)
这里为什么 没有
1
2
π
σ
\frac{1}{\sqrt{2\pi}\sigma}
2πσ1?有点不解。
在M步骤中再通过E步中计算的朗伯照明假设的概率,最大化反照率和法向的极大似然。
即最大化
P
(
Ω
)
P(\Omega)
P(Ω)
P
(
Ω
)
=
∑
k
log
P
(
O
k
,
H
k
=
1
∣
Ω
)
ω
k
+
∑
k
log
P
(
O
k
,
H
k
=
0
∣
Ω
)
(
1
−
ω
k
)
P(\Omega)=\sum_k\log P(O_k,H_k=1|\Omega)\omega_k+\sum_k\log P(O_k,H_k=0|\Omega)(1-\omega_k)
P(Ω)=k∑logP(Ok,Hk=1∣Ω)ωk+k∑logP(Ok,Hk=0∣Ω)(1−ωk)
=
∑
k
log
(
α
2
π
σ
exp
(
−
∥
ρ
⋅
s
k
(
n
)
−
I
k
W
∥
2
2
σ
2
)
)
ω
k
+
∑
k
log
(
1
−
α
C
)
(
1
−
ω
k
)
=\sum_k\log\bigg(\frac{\alpha}{\sqrt{2\pi}\sigma}\exp\big(-\frac{\parallel\rho\cdot s_k(n)-I_k^W\parallel^2}{2\sigma^2}\big)\bigg)\omega_k+\sum_k\log\big(\frac{1-\alpha}{C}\big)(1-\omega_k)
=k∑log(2πσαexp(−2σ2∥ρ⋅sk(n)−IkW∥2))ωk+k∑log(C1−α)(1−ωk)
对
P
(
Ω
)
P(\Omega)
P(Ω)中的
α
,
σ
,
ρ
\alpha,\sigma,\rho
α,σ,ρ三个变量求一阶导数并让它们分别等于0,最后解得
α
=
1
N
∑
k
ω
k
\alpha=\frac{1}{N}\sum_k\omega_k
α=N1k∑ωk
σ
=
∑
k
∥
ρ
⋅
s
k
(
n
)
−
I
k
W
∥
2
ω
k
∑
k
ω
k
\sigma=\sqrt{\frac{\sum_k\parallel\rho\cdot s_k(n)-I_k^W\parallel^2\omega_k}{\sum_k\omega_k}}
σ=∑kωk∑k∥ρ⋅sk(n)−IkW∥2ωk
ρ
=
1
∑
k
s
k
(
n
)
2
ω
k
∑
k
s
k
(
n
)
⋅
ω
k
⋅
I
k
W
\rho=\frac{1}{\sum_ks_k(n)^2\omega_k}\sum_ks_k(n)\cdot\omega_k\cdot I_k^W
ρ=∑ksk(n)2ωk1k∑sk(n)⋅ωk⋅IkW
更新完
α
,
σ
,
ρ
\alpha,\sigma,\rho
α,σ,ρ后通过求解
arg
min
n
∑
k
∥
ρ
⋅
(
n
T
R
k
T
A
R
k
n
+
b
T
R
k
n
+
c
)
−
I
k
W
∥
2
ω
k
\arg\min_n\sum_k\parallel\rho\cdot(n^TR_k^TAR_kn+b^TR_kn+c)-I_k^W\parallel^2\omega_k
argnmink∑∥ρ⋅(nTRkTARkn+bTRkn+c)−IkW∥2ωk
得到新的法向n。
迭代进行E步和M步。
最后,使用已有的方法,将法线与KinectFusion生成的三维模型进行融合,获得具有增强结构细节的表面几何结构。
3.实验结果
在实验中,使用Stanford Bunny作为合成模型,并在论文方法和shading refinement方法之间进行定量比较。 对于给出的3D模型,在自然照明下渲染20张RGB图像和深度图。 渲染的GT深度图被过度平滑以消除掉表面的细节。 这些平滑的深度图和渲染的彩色图像被作为输入:
可以看到论文中的方法在合成数据上能够良好的恢复之前被平滑的细节,尤其由于之前EM算法的应用,在图像上50%的像素都被椒盐噪声影响的情况下,也产生了良好的鲁棒性。
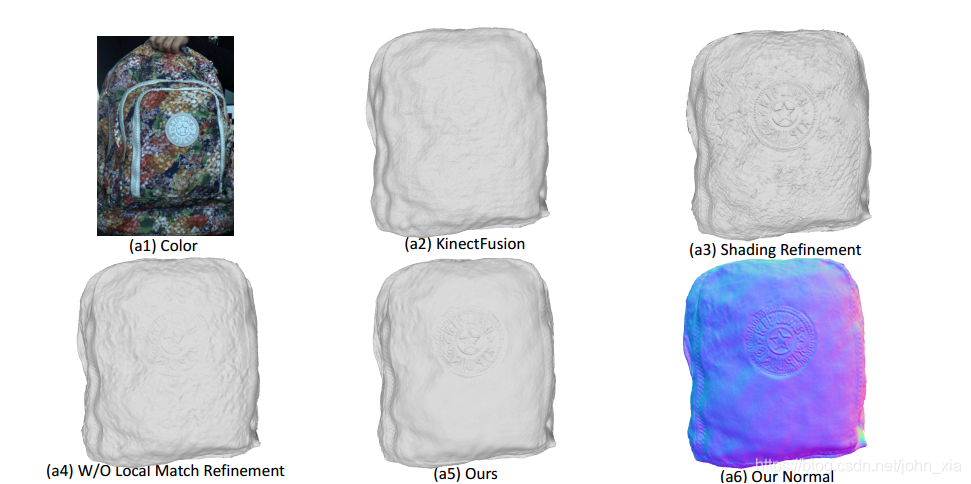
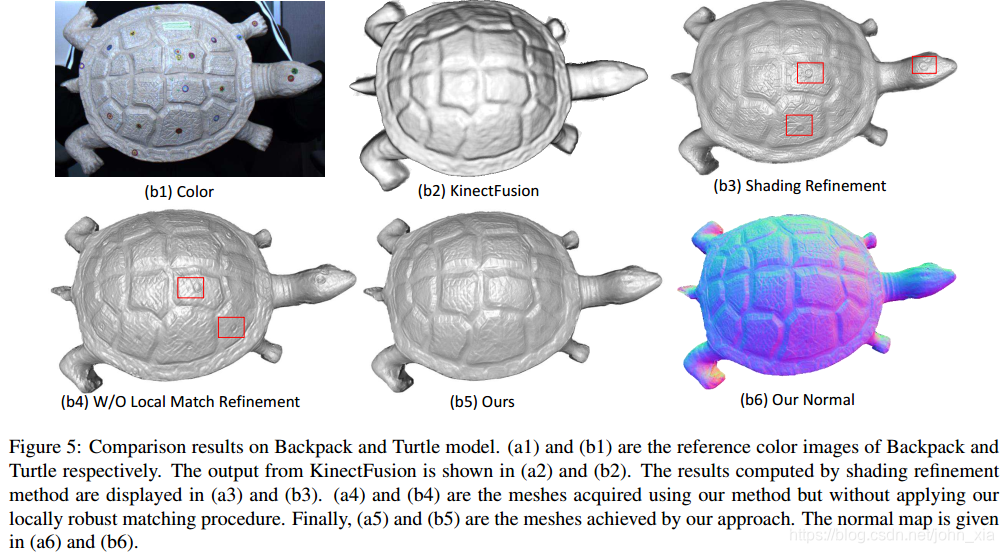
在真实数据上,使用Kinect V2的深度传感器和分辨率为1920×1080的彩色摄像机捕获了真实的数据进行实验,尤其可以注意到的是由于对单个像素进行处理,对于反照率能够产生良好的分解,在乌龟表面,其他方法将贴纸产生的颜色差异归因于表面的凹凸,而论文的方法很好的恢复了贴纸平面的效果: