typora markdown常用数学编辑公式
一、基本公式
1. 上下标
$$
A_1^2
\\
B_{12}
\\
2^{x^2+y}
$$
A 1 2 B 12 2 x 2 + y A_1^2 \\ B_{12} \\ 2^{x^2+y} A12B122x2+y
2. 分数
x 1 + x 2 1 2 + x y a b a b \frac{x}{1+x^2} \\ \frac{\frac{1}{2}+x}{y} \\ \tfrac{a}{b} \frac{a}{b} 1+x2xy21+xbaba
$$
\frac{x}{1+x^2}
\\
\frac{\frac{1}{2}+x}{y}
\\
\tfrac{a}{b}
\frac{a}{b}
$$
3. 开根号
x x 3 \sqrt{x} \sqrt[3]{x} x3x
$$
\sqrt{x}
\sqrt[3]{x}
$$
4. 组合数
( n k ) ( n k ) \binom{n}{k} \tbinom{n}{k} (kn)(kn)
$$
\binom{n}{k}
\tbinom{n}{k}
$$
5. 导数
a ′ a ′ ′ a ′ a' a'' a^{\prime} a′a′′a′
$$
a'
a''
a^{\prime}
$$
6. 取模
x ( m o d a ) 2 m o d x x \pmod a \\ 2\mod{x} x(moda)2modx
$$
x \pmod a
\\
2\mod{x}
$$
7. 积分
∫ 1 2 ∫ 2 1 ∮ ∫ ∬ ∯ ∭ ∰ \int_{1}^{2} \intop_{2}^{1} \oint \smallint \\ \iint \oiint \iiint \oiiint ∫122∫1∮∫∬∬∭∭
$$
\int_{1}^{2}
\intop_{2}^{1}
\oint
\smallint
\\
\iint
\oiint
\iiint
\oiiint
$$
8.微分
∇ ∂ x d x x ˙ y ¨ Δ \nabla \\ \partial x \\ \mathrm{d}x \\ \dot x \\ \ddot y \\ \Delta ∇∂xdxx˙y¨Δ
$$
\nabla
\partial x
\mathrm{d}x
\dot x
\ddot y
\Delta
$$
9.累积/累乘/极限
∑ i = 1 k ∑ i = 1 n ∑ i = 1 n ∏ i = 1 k ∏ i = 1 n ∏ i = 1 n lim k → ∞ lim k → ∞ lim k → ∞ \sum_{i=1}^{k} \displaystyle\sum_{i=1}^n \textstyle\sum_{i=1}^n \\ \prod_{i=1}^{k} \displaystyle\prod_{i=1}^n \textstyle\prod_{i=1}^n \\ \lim_{k \to \infty} \lim\limits_{k \to \infty} \lim\nolimits_{k \to \infty} i=1∑ki=1∑n∑i=1n∏i=1ki=1∏n∏i=1nlimk→∞k→∞limlimk→∞
$$
\sum_{i=1}^{k}
\displaystyle\sum_{i=1}^n
\textstyle\sum_{i=1}^n
\\
\prod_{i=1}^{k}
\displaystyle\prod_{i=1}^n
\textstyle\prod_{i=1}^n
\\
\lim_{k \to \infty}
\lim\limits_{k \to \infty}
\lim\nolimits_{k \to \infty}]
$$
二、修饰符号
1. 简单的帽子
θ ^ A B ^ y ˉ A B ‾ a ~ a c ~ a ˉ a ˊ a ˇ a ˋ a ˙ a ¨ \hat{\theta} \widehat{AB} \\ \bar{y} \overline{AB} \\ \tilde{a} \widetilde{ac} \\ \bar{a} \acute{a} \check{a} \grave{a} \\ \dot{a} \ddot{a} θ^AB yˉABa~ac aˉaˊaˇaˋa˙a¨
$$
\hat{\theta}
\widehat{AB}
\\
\bar{y}
\overline{AB}
\\
\tilde{a}
\widetilde{ac}
\\
\bar{a}
\acute{a}
\check{a}
\grave{a}
\\
\dot{a}
\ddot{a}
$$
2. 帽子和袜子
A B ← A B → A B ↔ A B ← A B → A B ↔ A B ⏞ A B ⏟ A B ‾ A B ‾ \overleftarrow{AB} \overrightarrow{AB} \overleftrightarrow{AB} \\ \underleftarrow{AB} \underrightarrow{AB} \underleftrightarrow{AB} \\ \overbrace{AB} \underbrace{AB} \\ \overline{AB} \underline{AB} ABABAB ABAB ABAB ABABAB
$$
\overleftarrow{AB}
\overrightarrow{AB}
\overleftrightarrow{AB}
\\
\underleftarrow{AB}
\underrightarrow{AB}
\underleftrightarrow{AB}
\\
\overbrace{AB}
\underbrace{AB}
\\
\overline{AB}
\underline{AB}
$$
3. 盒子和帽子
a + b + c ⏞ note a + b + c ⏟ note π = 3.14 \overbrace{a+b+c}^{\text{note}} \\ \underbrace{a+b+c}_{\text{note}} \\ \boxed{\pi=3.14} a+b+c notenote a+b+cπ=3.14
$$
\overbrace{a+b+c}^{\text{note}}
\\
\underbrace{a+b+c}_{\text{note}}
\\
\boxed{\pi=3.14}
$$
4. 各种括号
( ( ( ( ( ( \big( \Big( \bigg( \Bigg( (((((
$$
(
\big(
\Big(
\bigg(
\Bigg(
$$
[ ] < > ∣ − 2 ∣ { } [] <> |-2| \{\} []<>∣−2∣{}
$$
[]
<>
|-2|
\{\}
$$
⟮ x ⟯ ∥ a ∥ ⌈ 2.6 ⌉ ⌊ 1.2 ⌋ \lgroup x \rgroup \lVert a \rVert \lceil 2.6 \rceil \lfloor 1.2 \rfloor ⟮x⟯∥a∥⌈2.6⌉⌊1.2⌋
$$
\lgroup x \rgroup
\lVert a \rVert
\lceil 2.6 \rceil
\lfloor 1.2 \rfloor
⌜ ⌝ ⌞ ⌟ \ulcorner \urcorner \llcorner \lrcorner ┌┐└┘
\ulcorner
\urcorner
\llcorner
\lrcorner
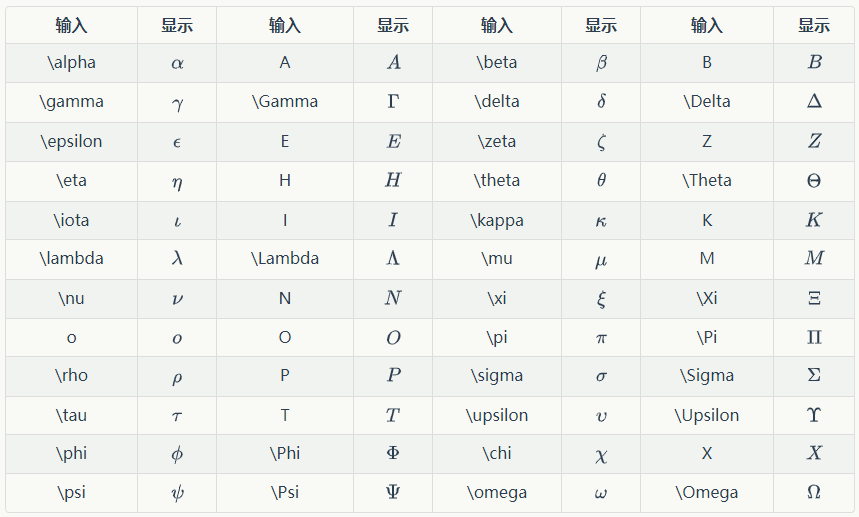
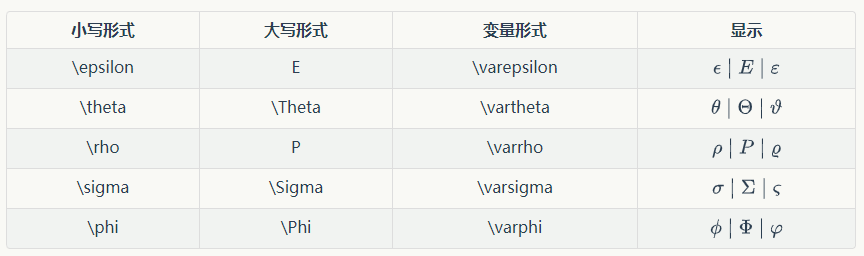
三、希腊字母
$$
| No. | Lowercase | Uppercase | English | IPA |
|---|---|---|---|---|
| 1 1 1 | α \alpha α | A A A | a l p h a alpha alpha | /'ælfə/ |
| 2 2 2 | β \beta β | B B B | b e t a beta beta | /'bi:tə/or/'beɪtə/ |
| 3 3 3 | γ \gamma γ | Γ \Gamma Γ | g a m m a gamma gamma | /'gæmə/ |
| 4 4 4 | δ \delta δ | Δ \Delta Δ | d e l t a delta delta | /'deltə/ |
| 5 5 5 | ϵ \epsilon ϵ | E E E | e p s i l o n epsilon epsilon | /'epsɪlɒn/ |
| 6 6 6 | ζ \zeta ζ | Z Z Z | z e t a zeta zeta | /'zi:tə/ |
| 7 7 7 | η \eta η | H H H | e t a eta eta | /'i:tə/ |
| 8 8 8 | θ \theta θ | Θ \Theta Θ | t h e t a theta theta | /'θi:tə/ |
| 9 9 9 | ι \iota ι | I I I | i o t a iota iota | /aɪ’əʊtə/ |
| 10 10 10 | κ \kappa κ | K K K | k a p p a kappa kappa | /'kæpə/ |
| 11 11 11 | λ \lambda λ | λ \lambda λ | l a m b d a lambda lambda | /'læmdə/ |
| 12 12 12 | μ \mu μ | M M M | m u mu mu | /mju:/ |
| 13 13 13 | ν \nu ν | N N N | n u nu nu | /nju:/ |
| 14 14 14 | ξ \xi ξ | Ξ \Xi Ξ | x i xi xi | /ksi/or/'zaɪ/or/'ksaɪ/ |
| 15 15 15 | ο \omicron ο | O O O | o m i c r o n omicron omicron | /əu’maikrən/or/'ɑmɪ,krɑn/ |
| 16 16 16 | π \pi π | Π \Pi Π | p i pi pi | /paɪ/ |
| 17 17 17 | ρ \rho ρ | P P P | r h o rho rho | /rəʊ/ |
| 18 18 18 | σ \sigma σ | Σ \Sigma Σ | s i g m a sigma sigma | /'sɪɡmə/ |
| 19 19 19 | τ \tau τ | T T T | t a u tau tau | /tɔ:/or/taʊ/ |
| 20 20 20 | υ \upsilon υ | Υ \Upsilon Υ | u p s i l o n upsilon upsilon | /'ipsilon/or/'ʌpsilɒn/ |
| 21 21 21 | ϕ \phi ϕ | Φ \Phi Φ | p h i phi phi | /faɪ/ |
| 22 22 22 | χ \chi χ | X X X | c h i chi chi | /kaɪ/ |
| 23 23 23 | ψ \psi ψ | Ψ \Psi Ψ | p s i psi psi | /psaɪ/ |
| 24 24 24 | ω \omega ω | Ω \Omega Ω | o m e g a omega omega | /'əʊmɪɡə/or/oʊ’meɡə/ |
| $$ |
四、算术运算符号
+ × / ÷ ⋅ # % + \times / \div \cdot \# \% +×/÷⋅#%
+
-
\times
/
\div
\cdot
\#
\%
∘ ∗ ⋆ ⊗ ⊕ ⊙ \circ \ast \star \otimes \oplus \odot ∘∗⋆⊗⊕⊙
\circ
\ast
\star
\otimes
\oplus
\odot
± ∓ ∔ ⋇ \pm \mp \dotplus \divideontimes ±∓∔⋇
\pm
\mp
\dotplus
\divideontimes
五、比较运算符
= ≢ ≈ ≊ ≅ ∼ ≠ ≠ = \not \equiv \approx \approxeq \cong \sim \neq \not= =≡≈≊≅∼==
=
= \not
\equiv
\approx
\approxeq
\cong
\sim
\neq
\not=
<
<
<
>
>
>
≤
\le
≤
≥
\ge
≥
≫
\gg
≫
≪
\ll
≪
<
>
\le
\ge
\gg
\ll
⋞ ⋟ ≺ ≻ ⪯ ⪰ \curlyeqprec \curlyeqsucc \prec \succ \preceq \succeq ⋞⋟≺≻⪯⪰
\curlyeqprec
\curlyeqsucc
\prec
\succ
\preceq
\succeq
六、集合运算符
∈ ∋ ⊄ ⊅ ⊆ ⊇ ∩ ∪ ∧ ∨ ¬ ∅ ∅ ∵ ∀ ∃ ∴ \in \owns \not \subset \not \supset \subseteq \supseteq \\ \cap \cup \land \lor \\ \neg \emptyset \varnothing \\ \because \forall \exists \therefore ∈∋⊂⊃⊆⊇∩∪∧∨¬∅∅∵∀∃∴
\in
\owns \not
\subset \not
\supset
\subseteq
\supseteq
\\
\cap
\cup
\land
\lor
\\
\neg
\emptyset
\varnothing
\\
\because
\forall
\exists
\therefore
∩ ∪ ∧ ∨ ⊔ ⊓ \cap \cup \land \lor \sqcup \sqcap ∩∪∧∨⊔⊓
\cap
\cup
\land
\lor
\sqcup
\sqcap
七、各种箭头
← ← → → ↔ ↑ ↓ ↕ \gets \leftarrow \to \rightarrow \leftrightarrow \\ \uparrow \downarrow \updownarrow ←←→→↔↑↓↕
\gets
\leftarrow
\to
\rightarrow
\leftrightarrow
\\
\uparrow
\downarrow
\updownarrow
⇐ ⇒ ⇔ ⟺ ⇑ ⇓ ⇕ \Leftarrow \Rightarrow \Leftrightarrow \iff \\ \Uparrow \Downarrow \Updownarrow ⇐⇒⇔⟺⇑⇓⇕
\Leftarrow
\Rightarrow
\Leftrightarrow
\iff
\\
\Uparrow
\Downarrow
\Updownarrow
↗ ↘ ↙ ↖ \nearrow \searrow \swarrow \nwarrow ↗↘↙↖
\nearrow
\searrow
\swarrow
\nwarrow
⟵ ⟶ ⟷ ⟸ ⟹ ⟺ ⟼ \longleftarrow \longrightarrow \longleftrightarrow \Longleftarrow \Longrightarrow \Longleftrightarrow \longmapsto ⟵⟶⟷⟸⟹⟺⟼
\longleftarrow
\longrightarrow
\longleftrightarrow
\Longleftarrow
\Longrightarrow
\Longleftrightarrow
\longmapsto
→ o v e r → o v e r → u n d e r o v e r ← o v e r ← u n d e r ← u n d e r o v e r \xrightarrow{over} \xrightarrow[over]{} \xrightarrow[under]{over} \xleftarrow[]{over} \xleftarrow[under]{} \xleftarrow[under]{over} overoveroverunderoverunderoverunder
\xrightarrow{over}
\xrightarrow[over]{}
\xrightarrow[under]{over}
\xleftarrow[]{over}
\xleftarrow[under]{}
\xleftarrow[under]{over}
七、空间间距
A B A B A B A B A B A B A B A B A\!B \\ AB \\ A\thinspace B \\ A\:B \\ A\ B \\ A \enspace B \\ A\quad B \\ A\qquad B ABABABABA BABABAB
A\!B
\\
AB
\\
A\thinspace B
\\
A\:B
\\
A\ B
\\
A \enspace B
\\
A\quad B
\\
A\qquad B
八、矩阵
A = a b c d A = \begin{matrix} a & b\\ c & d \end{matrix} A=acbd
A = \begin{matrix}
a & b\\
c & d
\end{matrix}
B = ( a b c d ) B = \begin{pmatrix} a & b\\ c & d \end{pmatrix} B=(acbd)
B = \begin{pmatrix}
a & b\\
c & d
\end{pmatrix}
C = ∣ a b c d ∣ C = \begin{vmatrix} a & b\\ c & d \end{vmatrix} C= acbd
C = \begin{vmatrix}
a & b\\
c & d
\end{vmatrix}
D = [ a b c d ] D = \begin{bmatrix} a & b\\ c & d \end{bmatrix} D=[acbd]
D = \begin{bmatrix}
a & b\\
c & d
\end{bmatrix}
E = ∥ a b c d ∥ E = \begin{Vmatrix} a & b\\ c & d \end{Vmatrix} E= acbd
E = \begin{Vmatrix}
a & b\\
c & d
\end{Vmatrix}
F = { a b c d } F = \begin{Bmatrix} a & b\\ c & d \end{Bmatrix} F={acbd}
F = \begin{Bmatrix}
a & b\\
c & d
\end{Bmatrix}
[ A b ] = [ a 11 a 12 a 13 b 1 a 21 a 22 a 23 b 2 a 31 a 32 a 33 b 3 ] [A\ b] = \begin{bmatrix} \begin{array}{c c c|c} a_{11} & a_{12} & a_{13} & b_1\\ a_{21} & a_{22} & a_{23} & b_2\\ a_{31} & a_{32} & a_{33} & b_3\\ \end{array} \end{bmatrix} [A b]= a11a21a31a12a22a32a13a23a33b1b2b3
[A\ b] =
\begin{bmatrix}
\begin{array}{c c c|c}
a_{11} & a_{12} & a_{13} & b_1\\
a_{21} & a_{22} & a_{23} & b_2\\
a_{31} & a_{32} & a_{33} & b_3\\
\end{array}
\end{bmatrix}
a b c d e f g h i \begin{array}{c:c:c} a & b & c \\ \hline d & e & f \\ \hdashline g & h & i \end{array} adgbehcfi
\begin{array}{c:c:c}
a & b & c \\
\hline
d & e & f \\
\hdashline
g & h & i
\end{array}
L n × n = [ a 11 a 12 ⋯ a 1 n a 21 a 22 ⋯ a 2 n ⋮ ⋮ ⋱ ⋮ a n 1 a n 2 ⋯ a n n ] L_{n\times n} = \begin{bmatrix} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots &\ddots & \vdots\\ a_{n1} & a_{n2} & \cdots & a_{nn} \\ \end{bmatrix} Ln×n= a11a21⋮an1a12a22⋮an2⋯⋯⋱⋯a1na2n⋮ann
L_{n\times n} = \begin{bmatrix}
a_{11} & a_{12} & \cdots & a_{1n} \\
a_{21} & a_{22} & \cdots & a_{2n} \\
\vdots & \vdots &\ddots & \vdots\\
a_{n1} & a_{n2} & \cdots & a_{nn} \\
\end{bmatrix}
八、列式/方程组
f ( x ) = ( x + 1 ) 2 = x 2 + 2 x + 1 \begin{aligned} f(x) &= (x+1)^2\\ &= x^2 + 2x + 1 \end{aligned} f(x)=(x+1)2=x2+2x+1
\begin{aligned}
f(x) &= (x+1)^2\\
&= x^2 + 2x + 1
\end{aligned}
f ( x ) = { a if b b if a f(x) = \begin{cases} a &\text{if b}\\ b &\text{if a}\\ \end{cases} f(x)={abif bif a
f(x) = \begin{cases}
a &\text{if b}\\
b &\text{if a}\\
\end{cases}
{ x + 2 y = 1 3 x − y = 5 \begin{cases} \begin{aligned} x + 2y &= 1\\ 3x - y &= 5 \end{aligned} \end{cases} {x+2y3x−y=1=5
\begin{cases}
\begin{aligned}
x + 2y &= 1\\
3x - y &= 5
\end{aligned}
\end{cases}
g ( x , y ) = { d b ≤ f ( x , y ) ≤ M f F L ∗ S L ≤ 0 < S M F R ∗ S M ≤ 0 < S R F R S R ≤ 0 g(x,y)=\left\{ \begin{array}{rcl} d & & {b \leq f(x,y) \leq M_f}\\ F^*_L & & {S_L \leq 0 < S_M}\\ F^*_R & & {S_M \leq 0 < S_R}\\ F_R & & {S_R \leq 0} \end{array} \right. g(x,y)=⎩ ⎨ ⎧dFL∗FR∗FRb≤f(x,y)≤MfSL≤0<SMSM≤0<SRSR≤0
g(x,y)=\left\{
\begin{array}{rcl}
\frac{M_g - d}{M_f-b}[f(x,y)-b]+d & & {b \leq f(x,y) \leq M_f}\\
F^*_L & & {S_L \leq 0 < S_M}\\
F^*_R & & {S_M \leq 0 < S_R}\\
F_R & & {S_R \leq 0}
\end{array} \right.
#九、修改颜色和字体大小
F = m a F = m a F = m a o n e l i n e n o t h i n g \textcolor{blue}{F=ma} \\ \textcolor{#00ff00}{F=ma} \\ \textcolor{#ff0000}{F=ma} \\ \color{blue} one\ line \\ nothing F=maF=maF=maone linenothing
\textcolor{blue}{F=ma}
\\
\textcolor{#00ff00}{F=ma}
\\
\textcolor{#ff0000}{F=ma}
\\
\color{blue} one\ line
\\
nothing
F=ma A A \colorbox{#00ff00}{F=ma} \\ \colorbox{aqua}{A} \\ \fcolorbox{red}{aqua}{A} F=maAA
\colorbox{#00ff00}{F=ma}
\\
\colorbox{aqua}{A}
\\
\fcolorbox{red}{aqua}{A}
A B A B A B A B A B A B A B A B A B A B AB \Huge AB \huge AB \\ AB \LARGE AB \Large AB \large AB \\ AB \small AB \tiny AB ABABABABABABABABABAB
AB
\Huge AB
\huge AB
\\
AB
\LARGE AB
\Large AB
\large AB
\\
AB
\small AB
\tiny AB
十、划掉
5 5 A B C ≠ \cancel{5} \bcancel{5} \xcancel{ABC} \not = 5 5 ABC =
\cancel{5}
\bcancel{5}
\xcancel{ABC}
\not =
十一、常见图形
□ □ ■ △ ▽ ▲ ⋄ ◊ ⋆ ★ ∘ ∙ ◯ ⨀ \Box \square \blacksquare \triangle \triangledown \blacktriangle \diamond \Diamond \star \bigstar \circ \bullet \bigcirc \bigodot □□■△▽▲⋄◊⋆★∘∙◯⨀
\Box
\square
\blacksquare
\triangle
\triangledown
\blacktriangle
\diamond
\Diamond
\star
\bigstar
\circ
\bullet
\bigcirc
\bigodot
♢ ♣ ♡ ♠ \diamondsuit \clubsuit \heartsuit \spadesuit ♢♣♡♠
\diamondsuit
\clubsuit
\heartsuit
\spadesuit
∠ ∡ ⊤ ⊥ ∞ \angle \measuredangle \top \bot \infty ∠∡⊤⊥∞
\angle
\measuredangle
\top
\bot
\infty
✓ † ‡ ¥ $ \checkmark \dagger \ddagger \yen \$ ✓†‡¥$
\checkmark
\dagger
\ddagger
\yen
\$
十二、声明宏
对于一些复杂但是只有少许不同的表达式,可以声明一个函数来调用,提高源码的可读性,减少出错
\def\macroname#1#2{
your command
}
宏允许带任意数量的参数(也可以不带参),必须是#1,#2,……这样的命名格式,同时注意再定义宏的时候注意让#1与\中间隔一个空格,否则会解析成#。再调用的时候格式为\macroname{x}{y}{z},可以参考一下的例子
f
(
x
)
=
1
2
π
σ
1
exp
[
−
(
x
−
u
1
)
2
2
σ
1
2
]
f
(
y
)
=
1
2
π
σ
2
exp
[
−
(
y
−
u
2
)
2
2
σ
2
2
]
\def\Normal#1#2#3{ \frac{1}{\sqrt{2\pi}\ #3}\exp{[-\frac{(#1 - #2)^2}{2\ #3^2}]} } f(x)=\Normal{x}{u_1}{\sigma_1}\\ f(y)=\Normal{y}{u_2}{\sigma_2}\\
f(x)=2π σ11exp[−2 σ12(x−u1)2]f(y)=2π σ21exp[−2 σ22(y−u2)2]
\def\Normal#1#2#3{
\frac{1}{\sqrt{2\pi}\ #3}\exp{[-\frac{(#1 - #2)^2}{2\ #3^2}]}
}
f(x)=\Normal{x}{u_1}{\sigma_1}\\
f(y)=\Normal{y}{u_2}{\sigma_2}\\
e x = 1 + x + 1 2 ! x 2 + 1 3 ! x 3 + ⋯ \def\EXP{ e^x = 1 + x + \frac{1}{2!}x^2 + \frac{1}{3!}x^3 + \cdots } \EXP ex=1+x+2!1x2+3!1x3+⋯
\def\EXP{
e^x = 1 + x + \frac{1}{2!}x^2 + \frac{1}{3!}x^3 + \cdots
}
\EXP