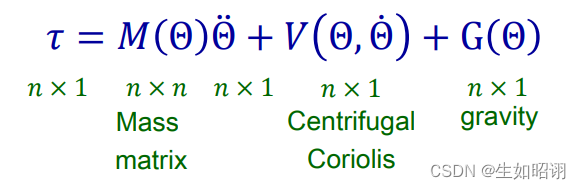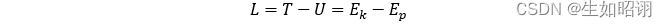前言

在上一节的机器人学习中，我们已经了解到当下热门的机器人研究方向，从视觉、人工智能到多机通讯、人机协同，机器人的研究有着广阔的前景，而想要学好机器人，第一步就是要首先建立模型，本节的标题是数学意义上的建模及仿真，实际上是指对机器人进行运动学模型和动力学模型的构建，并使用Matlab的工具箱完成对于模型的验证仿真。下节将会是机械意义上的机器人建模，指如何手动生成建立图形化的机器人3D模型，涉及到诸多仿真软件，在下一节博客中，将会附带平面2R机器人和四足机器人单腿模型的示例分析。

一、模型概念

1. 建立模型的意义

• 运动学模型：描述控制对象的目标运动和每个驱动单元运动之间的关系，在控制过程中反复调用

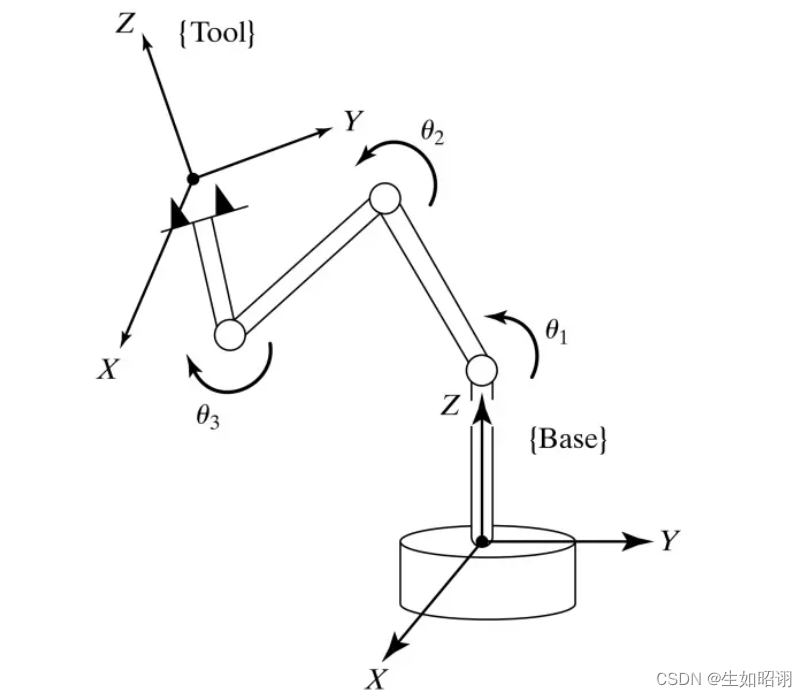
简单的讲：正如我们谈到的坐标变换，运动学模型给了我们末端执行器或者其他坐标系相对于机器人的躯干坐标系等之间的关系，方便进行运动正逆结算，可以直接通过对于末端轨迹进行规划，通过运动学模型得到各位置移动轨迹；

• 动力学模型：描述被控对象的运动和驱动单元输入力或力矩的关系。确定运动指标的上限以及指导进行器件选型

简单的讲：有了机器人各部分的运动情况，想要实现对于机器人的控制，就需要通过动力学模型完成从运动位移角度到力学角度，即各关节力矩的转换，从而实现控制；

2. 建立模型的方法

即，使用什么方法建立机器人模型？

1）运动学模型：

历史方法演变

1. 刚体运动学方法：针对于刚体系统，也就是把物体在力作用下的变形忽略，简化问题，利用达朗贝尔-拉格朗日原理进行数学建模，计算相对较为复杂；
2. 多体系统：更多用于分析复杂机械系统，容易实现计算机的自动编程，更加规范化、程式化，在多体复杂系统中占有重要地位
3. 机构学建模法：从机构学出发，将机器人进行层层分解，拆分复杂杆组，利用图论等原理将子系统、机构之间的关系转化为矩阵练习，确定机体自由与冗余情况，其中最著名的就是齐次坐标矩阵法。

主流方法：DH模型方法
我们常用的运动学建模方法有DH模型方法，四元数方法，指数积方法等，这里重点介绍DH模型方法

• 概念：利用齐次变换矩阵描述相邻连杆空间关系，通过层层变换，实现从基坐标系到末端执行器坐标系的等价齐次变换矩阵，即运动学方程。把机器人操作臂看做一系列连杆通过移动和旋转关节串联而成，研究各连杆间运动位移、速度、加速度关系。

• 特点：概念更加清晰，在规定好各连杆坐标系、确定连杆参数后有着更加简单、直观的模型推导过程，并且容易在matlab中进行仿真；指数积方法则虽然不需要规定各连杆坐标系，只需要规定各关节矢量，但是计算量更大；对于四元数来说，则显得没有那么直观，理解相对困难。

2）动力学模型：

我们常用的运动学建模方法有拉格朗日方法、牛顿-欧拉方法、罗伯逊-魏登堡方法、凯恩方法等，这里重点介绍前两种方法

• 牛顿欧拉方法：

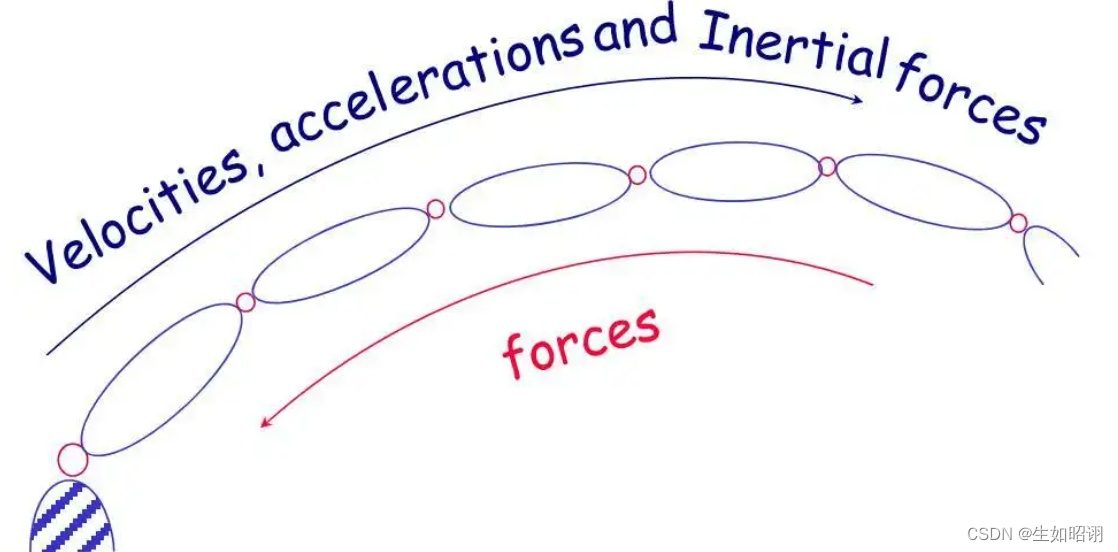
通过达朗贝尔原理和运动坐标系的概念建立相应方程，将刚体的运动主要分为平动和转动，对于质心乃至整个刚体的平动方面采用牛顿方程，应用动量定理，得出质心平动运动方程；对于转动方面使用欧拉方程，应用动量矩定理决定主力矩。严格遵守达朗贝尔定理，对于每个杆件的运动都考虑外部驱动和惯性力两部分，以二者的代数和为零作为基本条件，实现精确计算。这种方法计算速度很快，能够有效过滤冗余信息，是较为常用的方法之一。

• 拉格朗日动力学方法：

一种基于能量平衡的方法，在处理简单系统时比牛顿-欧拉方法会复杂很多，但是随着系统复杂性增加，会相对更加简单。它主要通过设定广义坐标，描述机器人受力情况，不需要求解复杂的内部作用力，通过能量对于时间和对应变量的微分结果建立方程，更加直观清晰。

注：不同于运动学模型，建立动力学模型只是对于机器人控制的一种手段，基于动力学模型的控制方法在近年来于众多机器人中取得了非常令人满意的结果，尤其是对于对于串联机械臂来说，能够实现不错的控制效果，但是对于一些特殊机器人来说其实收到很大限制

二、建模方法分析

1. DH模型方法

1）基本思想

• 基本原理：将操作臂看做是由旋转关节和移动关节构成，各关节与自由度相对应。四足机器人的腿部结构可以通过连杆和转动关节表示。连杆0作为基座静止，长度为0，不计算在机器人连杆之内，末端执行器和连杆n固接一体，构成单链开式运动结构。

第一步，建立各关节坐标系

1. 每个连杆都固接着坐标系，其中基坐标系与基座固接，与连杆i固接的坐标系叫坐标系{i}，各坐标系的具体建立方法如下：
   
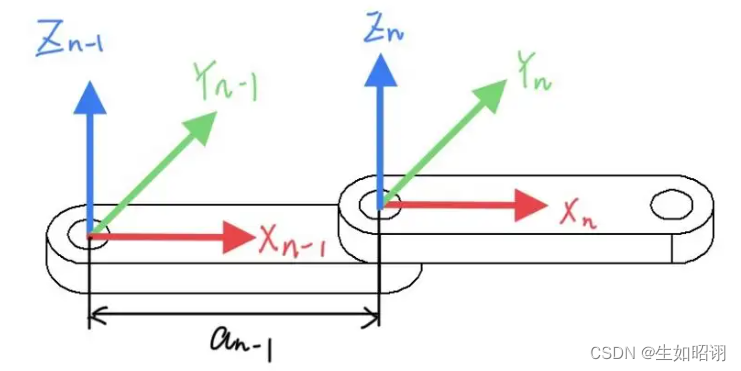
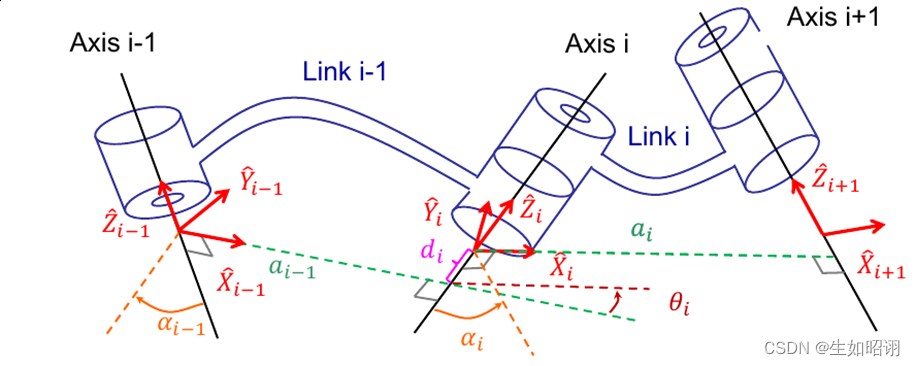
2. 连杆参数的具体定义，如图所示，连杆i-1由前后关节轴线的公法线长度a(i-1)以及两轴线间的夹角α(i-1)规定，关于单个连杆的参数定义如下：
   
   
   

第二步，连杆变换与运动学方程

1. 连杆之间的联系由上述四个参数组成，故两个坐标系之间的变换就是四个参数的函数，变换矩阵T可以视为由四个基本变换矩阵相乘得到：
   
2. 各连杆矩阵顺序相乘得到末段连杆坐标系{n}相对于基坐标系的变换矩阵，带入参数，即可得到运动学方程，建立起各关节变量与末端位姿之间的关系：
   

2）正逆问题

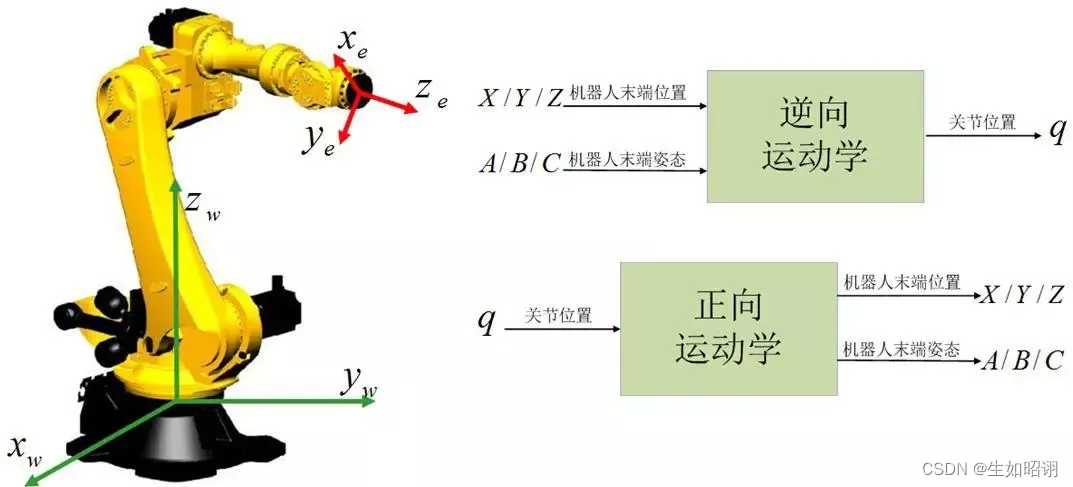
• 正问题：给定机器人关节变量的取值来确定末端执行器的位置和姿态
• 逆问题：根据给定的末端执行器的位置和姿态来确定机器人关节变量的取值

对于正问题来说，建立运动学方程的方法就是通过齐次变换矩阵相乘得到，而逆问题的求解相对复杂：

• 特点：运动学正解拥有唯一确定的解，即给出各关节变量就能得到唯一的末端执行器位姿，而运动学反解往往具有多重解，甚至不存在。运动学逆解的形式包括解析解和数值解，其中非线性超越方程一般只能采用数值解法，而解析解的求法包括几何法和代数法，在最为理想的情况下可以得到封闭解，封闭解法计算效率高、速度快，容易实现快速的控制；
• 方法：

1. 几何法：通过三角函数和相关定理，通过几何变换从数学的角度根据解的存在性条件和实际要求得出结果，在连杆多于两条相对较难处理。
2. 代数法：反变换法，主要内容就是用未知的逆变换逐次左乘运动学方程，以期实现分离关节变量并解出对应结果。

3）标准DH模型

注意：在上述的矩阵描述中，我们采用的改进DH模型，即Modified DH模型方法

• 标准DH模型：总体步骤相同，主要是坐标系与连杆的固接对应关系不同，以及齐次变换时的变换步骤不同

1. 坐标系：标准DH模型的坐标系i-1固接于连杆i上
2. 齐次变换步骤：
   

• 特点：一般选用MDH模型，Modified DH模型采用了一种新的连杆约束，对于连杆参数的反应在某些方面更加清晰和真实。相比于标准模型，MDH模型坐标系使用了一种统一的定义方法，可以更好的处理树结构、闭环结构等更多问题，建模过程更加灵活方便

2. 拉格朗日动力学方法

1）基本思想

• 拉格朗日函数L：系统的动能T(Ek)与势能U(Ep)之差，对于所有机械系统而言可用任意坐标系表示,笛卡尔坐标也适用；

• 动力学方程：
  

• 基本步骤：
  

2）正逆问题

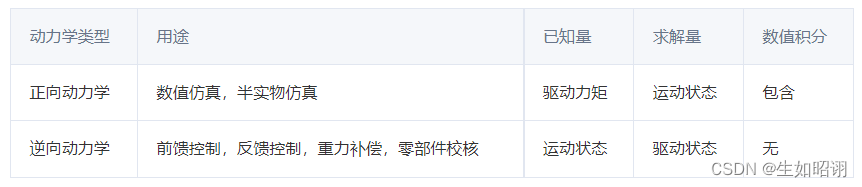
• 正问题：已知控制变量，即各关节驱动力矩和驱动力，根据物理定律，计算关节运动状态，包括位移、速度和加速度；

• 逆问题：在已知关节运动轨迹的情况下逆向求解关节控制力矩和驱动力；