问题描述

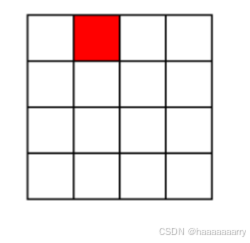
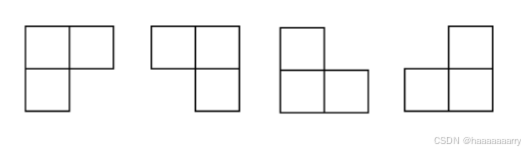
在一个$2^k\times 2^k$大小的棋盘中，有一个与其他方块不同的特殊方块，如下图红色方块。另有4种形态不同的L型骨块（见下图），要用图示四种骨块覆盖棋盘上除特殊方格外的其他所有方格，且任何两个L型骨块不得重叠。

问题分析

对于一个大棋盘，可将其横竖分成等大的四个子棋盘，每个棋盘大小为$2^k\times 2^k$，分成四个子问题，减小问题规模。但这四个子棋盘中只有一个子棋盘有特殊方块的存在，四个子问题不相同，不符合分治法的要求。

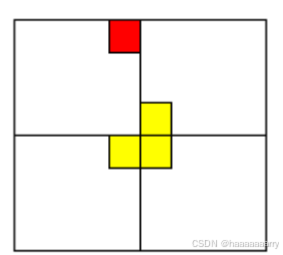
为了使子问题满足分治法的条件，可以在大棋盘中央覆盖一个L型骨块（见下图），将该骨块视为特殊方块，这样每个子棋盘中都有一个特殊方块，四个子问题相同，可以使用分治法解决。

递归的将大棋盘分成子棋盘，直到分割成1x1的方块，此时该子棋盘有且仅有一个被覆盖好的特殊方块，就不需要再做处理了

这样，这个问题就解决了

代码思路

函数声明：

void chessBoard(int tr, int tc, int dr, int dc, int size);

参数解释：

1. tr (top row):

   • 意义：当前子棋盘的左上角所在的行号。
   • 作用：用于确定当前子棋盘在整个棋盘中的位置。递归调用时，tr 会随着子棋盘的分割而变化。

2. tc (top column):

   • 意义：当前子棋盘的左上角所在的列号。
   • 作用：与 tr 类似，用于确定当前子棋盘在整个棋盘中的位置。递归调用时，tc 也会随着子棋盘的分割而变化。

3. dr (defect row):

   • 意义：特殊方格所在的行号。
   • 作用：用于确定特殊方格在当前子棋盘中的位置。递归调用时，dr 会与当前子棋盘的边界进行比较，以确定特殊方格是否在当前子棋盘中。

4. dc (defect column):

   • 意义：特殊方格所在的列号。
   • 作用：与 dr 类似，用于确定特殊方格在当前子棋盘中的位置。递归调用时，dc 会与当前子棋盘的边界进行比较，以确定特殊方格是否在当前子棋盘中。

5. size:

   • 意义：当前子棋盘的大小（边长）。
   • 作用：用于确定当前子棋盘的尺寸。每次递归调用时，size 会减半，直到 size 为 1 时递归终止。

函数体

在函数中，size=1为递归边界，size不为1时，将当前的骨块标号tile赋给变量t，同时tile自增1。并将分割后的子棋盘大小size/2赋给变量s。

二维数组board用于存储覆盖该位置的骨牌标号。

函数主体由四部分组成，每一部分分别覆盖左上角、右上角、左下角、右下角子棋盘

以左上角为例：

• 如果特殊方格在此棋盘中，递归调用自身，继续覆盖当前子棋盘的左上角子棋盘
• 如果特殊方格不在此棋盘中，用t号骨牌覆盖其右下角，并将其作为特殊方块，递归调用自身，覆盖其余方块

代码如下：

	//覆盖左上角子棋盘
	if (dr < tr + s && dc < tc + s)//特殊方格在此棋盘中
		chessBoard(tr, tc, dr, dc, s);
	else {	//特殊方格不在此棋盘中
		board[tr + s - 1][tc + s - 1] = t;//用t号骨牌覆盖右下角
		chessBoard(tr, tc, tr + s - 1, tc + s - 1, s);//覆盖其余方格
	}

重复上述过程，对左上角、右上角、左下角、右下角子棋盘均进行覆盖

递归过程：

• 基本情况：当 size == 1 时，递归终止，因为此时棋盘已经无法再分割。
• 递归情况：
  • 将当前棋盘分成四个大小相等的子棋盘。
  • 检查特殊方格是否在某个子棋盘中：
    • 如果在，则递归处理该子棋盘。
    • 如果不在，则在该子棋盘的适当位置放置一个L型骨牌，并递归处理该子棋盘。

示例：

假设有一个 8x8 的棋盘，特殊方格位于 (3, 4)，初始调用为 chessBoard(0, 0, 3, 4, 8)。

1. 第一次调用：

   • tr = 0, tc = 0, dr = 3, dc = 4, size = 8
   • 将棋盘分成四个 4x4 的子棋盘。
   • 检查特殊方格 (3, 4) 是否在左上角子棋盘 (0,0) 到 (3,3) 中。不在，因此在右下角放置一个L型骨牌，并递归处理左上角子棋盘。

2. 递归调用：

   • 对于左上角子棋盘，调用 chessBoard(0, 0, 3, 3, 4)。
   • 继续分割和递归，直到 size == 1。

通过这种方式，函数会递归地覆盖整个棋盘，确保每个子棋盘都被正确覆盖，最终完成棋盘覆盖问题的解决。

实例代码

对一个 8x8 的棋盘，特殊方格位于 (3, 4)，对其标记-1，进行覆盖，并输出覆盖后的棋盘

#include<stdio.h>
#define MAX_SIZE 8
int tile = 1;
int board[MAX_SIZE][MAX_SIZE];
void chessBoard(int tr, int tc, int dr, int dc, int size) {
	if (size == 1)
		return;
	int t = tile++;//L型骨牌号
	int s = size / 2;//分割棋盘
	//覆盖左上角子棋盘
	if (dr < tr + s && dc < tc + s)//特殊方格在此棋盘中
		chessBoard(tr, tc, dr, dc, s);
	else {	//特殊方格不在此棋盘中
		board[tr + s - 1][tc + s - 1] = t;//用t号骨牌覆盖右下角
		chessBoard(tr, tc, tr + s - 1, tc + s - 1, s);//覆盖其余方格
	}
	//覆盖右上角子棋盘
	if (dr < tr + s && dc >= tc + s)//特殊方格在此棋盘中
		chessBoard(tr, tc + s, dr, dc, s);
	else {	//特殊方格不在此棋盘中
		board[tr + s - 1][tc + s] = t;//用t号骨牌覆盖右下角
		chessBoard(tr, tc + s, tr + s - 1, tc + s, s);//覆盖其余方格
	}
	//覆盖左下角子棋盘
	if (dr >= tr + s && dc < tc + s)//特殊方格在此棋盘中
		chessBoard(tr + s, tc, dr, dc, s);
	else {	//特殊方格不在此棋盘中
		board[tr + s][tc + s - 1] = t;//用t号骨牌覆盖右下角
		chessBoard(tr + s, tc, tr + s, tc + s - 1, s);//覆盖其余方格
	}
	//覆盖右下角子棋盘
	if (dr >= tr + s && dc >= tc + s)//特殊方格在此棋盘中
		chessBoard(tr + s, tc + s, dr, dc, s);
	else {	//特殊方格不在此棋盘中
		board[tr + s][tc + s] = t;//用t号骨牌覆盖右下角
		chessBoard(tr + s, tc + s, tr + s, tc + s, s);//覆盖其余方格
	}
}
int main() {
	int size = MAX_SIZE;
	int dr = 3, dc = 4;
	board[dr][dc] = -1; // 特殊方格
	chessBoard(0, 0, dr, dc, size);
	for (int i = 0; i < size; i++)
	{
		for (int j = 0; j < size; j++) {
			printf("%2d ", board[i][j]);
		}
		printf("\n");
	}
	return 0;
}

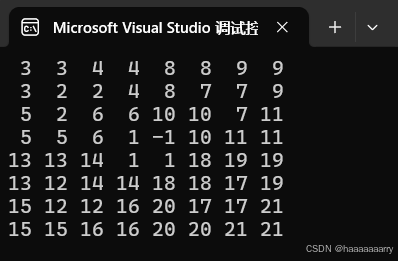
运行结果

可以看出，除标记为-1的位置（特殊方块）为覆盖外，其他的方格均被相应标号的骨块覆盖

为了计算棋盘覆盖算法的时间复杂度，我们可以分析递归调用的次数以及每次递归调用的工作量。

算法分析：

1. 递归关系：

   • 每次递归调用将棋盘分成四个大小相等的子棋盘。
   • 每次递归调用处理一个大小为 $$\frac{n}{2}\times \frac{n}{2}$$ 的子棋盘。
   • 递归终止条件是当棋盘大小为 1 x 1 时。

2. 递归树：

   • 每次递归调用会产生四个子问题，每个子问题的规模是原问题的一半。
   • 递归树的深度为 $${\log }_{2}n$$ 因为每次递归调用将问题规模减半。

3. 工作量：

   • 每次递归调用的工作量是常数时间 O(1) ，因为主要操作是检查特殊方格的位置和放置L型骨牌。

时间复杂度计算：

1. 递归调用次数：

   • 每次递归调用会产生四个子问题，因此递归调用的总次数为 $$4^{lo{g}_{2}n}$$
   • 由于 $$4^{{\log }_{2}n}=(2^2{)}^{{\log }_{2}n}=2^{2{\log }_{2}n}=n^2$$所以递归调用的总次数为 O(n^2) 。

2. 每次递归调用的工作量：

   • 每次递归调用的工作量是常数时间 O(1) 。

3. 总时间复杂度：

   • 总时间复杂度为递归调用次数乘以每次递归调用的工作量，即 $$O(n^2)\times O(1)=O(n^2)$$

详细计算过程：

1. 递归关系式：

   • 设 T(n) 为处理大小为 n x n 的棋盘的时间复杂度。
   • 递归关系式为：
     $$T(n)=4T\left(\frac{n}{2}\right)+O(1)$$

2. 展开递归关系式：

   • 展开递归关系式：
     $$T(n)=4T\left(\frac{n}{2}\right)+O(1)$$
     $$T\left(\frac{n}{2}\right)=4T\left(\frac{n}{4}\right)+O(1)$$
     $$T\left(\frac{n}{4}\right)=4T\left(\frac{n}{8}\right)+O(1)$$
     $$⋮$$
     $$T(1)=O(1)$$

3. 求和：

   • 将递归关系式展开后，总时间复杂度为：
     $$T(n)=4^{{\log }_{2}n}\times O(1)=n^2\times O(1)=O(n^2)$$

综上，棋盘覆盖算法的时间复杂度为 $O(n^2)$，其中 n 是棋盘的边长。这是因为每次递归调用将问题规模减半，但每次递归调用会产生四个子问题，最终递归调用的总次数为 $O(n^2)$。