安全多方计算
Lecture 1 安全多方计算(MPC)的基本概念及基础组件 —— 冯登国院士_哔哩哔哩_bilibili
安全多方计算定义与应用
安全多多方计算起源于姚启智教授于1982年在论文《Protocols for Secure computation》中以百万富翁问题(两个百万富翁A和B想知道他们两个谁更富有,但他们都不想让对方及其第三方指导自己财富的任何信息)提出。
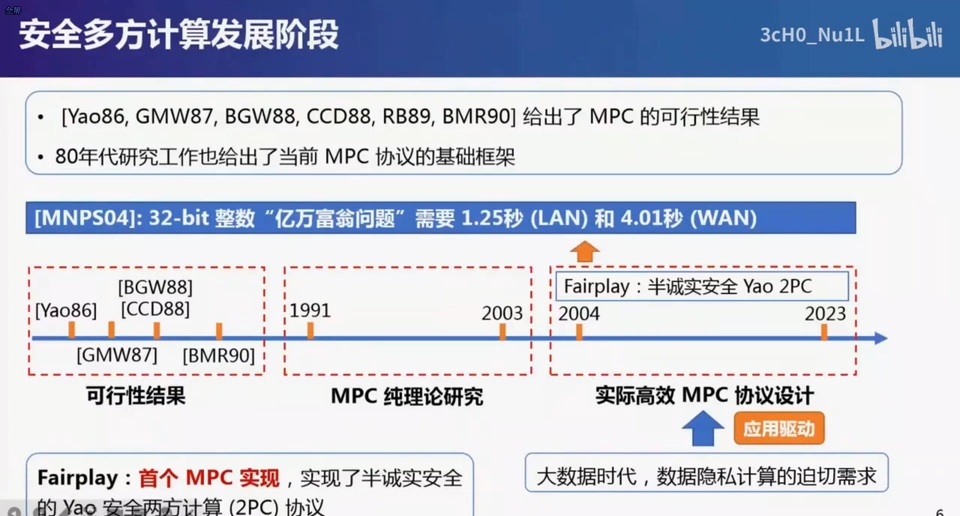
Fairplay首个MPC实现. 实现了半诚实安全(姚启智提出的两方安全计算协议),使学术界和工业界看到MPC协议是可实现的,可用于解决实际问题,04年之后随着大数据时代的到来,数据隐私计算的驱动,大量MPC的故作致力于实际高效设计,不断提高MPC协议的性能,推动MPC协议的实际应用。
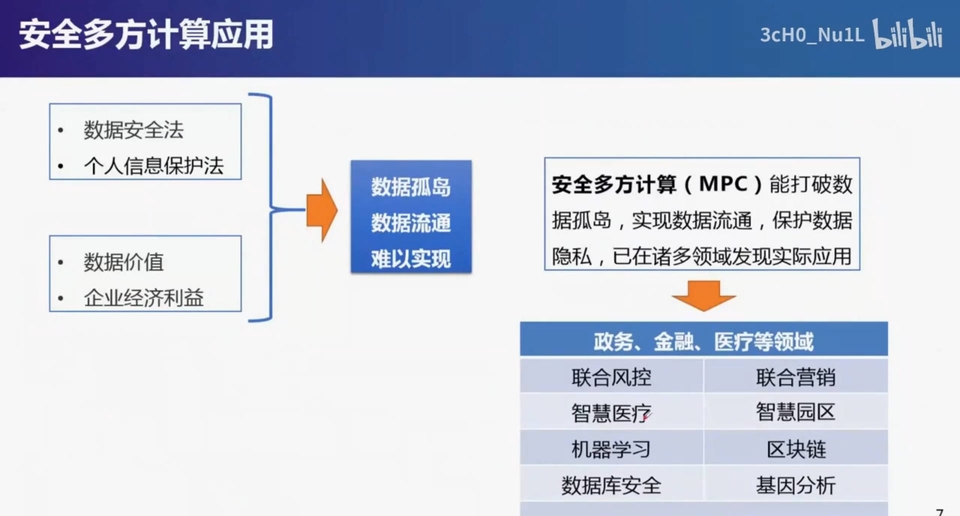
随着数据安全法和个人信息保护法的颁布,并且数据价值和企业经济利益,使数据形成一座座孤岛,数据流通难以实现。
MPC能打破数据孤岛,实现数据流通,保护数据隐私,并在诸多领域发现实际应用。
安全多方分类
MPC 协议需要满足隐私性 (privacy) 和正确性 (correctness) 两个基本安全属性.
(1) 敌手行为
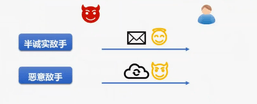
半诚实敌手:按照协议描述执行,但试图从协议记录中获取信息
恶意敌手:可以执行任何攻击,发送任意的消息
(2) 腐化数量(腐化门限t)
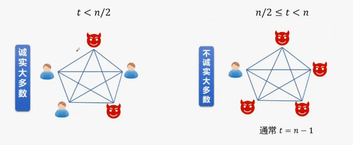
不诚实大多数情况, 其中 n/2 ⩽ t < n (大部分 MPC 协议考虑 t = n − 1);
诚实大多数情况, 其中 t < n/2 (即允许严格少于一半数量的参与方被敌手腐化).
(3) 输出的可达性
中止安全:腐化实体获得输出后,介意阻止诚实实体获得输出
公平性: 要么腐化实体和诚实实体均获得输出,要么他们均没有输出
保证输出传送: 所有城市实体总是获得输出
(4) 计算模型
布尔电路: 由AND,XOR,NOT等逻辑门组成
算术电路: 由AND,MULT等运算组成,通常定义在域
F
\mathbb{F}
F上或环
Z
2
k
\mathbb{Z}_{2^k}
Z2k(即
m
o
d
2
k
mod 2^k
mod2k)上
RAM程序: 由read,wrire等指令组成的程序
[!tip] 注意
大部分MPC协议考虑布尔电路模型或算术电路模型
目前,只有少数MPC协议针对RAM计算模型设计,适合于输入为数据库的引用场景
(5) 敌手计算能力(计算资源)
概率多项式时间(PPT):任意PPT敌手不能打破协议安全性
无限性计算能力(信息论安全或无条件安全): 即使用无限计算能力的敌手也不能打破协议安全性(抵抗量子计算机攻击)
信息论安全MPC协议需要再诚实大多数模型下设计
(6) 腐化策略
静态腐化: 在协议运行前,敌手决定腐化(Corrupt)哪些实体
自适应腐化:在协议运行过程中,敌手能自适应决定腐化哪些实体
目前, 高效的 MPC 协议设计主要考 虑的是静态腐化, 而满足自适应腐化安全性的 MPC 协议通常效率较低
(7) 网络模型
同步网络模型: 同一个交互轮的信息在固定延时
Δ
\Delta
Δ 内一定到达
异步网络模型: 没有要求同步时钟,也没有要求预先固定的网络延时,更加现实的网络假设(通常要求
t
<
n
/
3
t<n/3
t<n/3)
已知高效的MPC协议均考虑同步网络模型
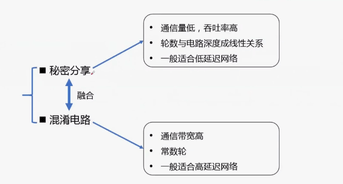
MPC 基本设计方法
秘密分享:具有较低的通信宽带,但轮数复杂度为O(d),适用于低延迟网络(局域网),其中d代表电路深度
混淆电路:轮数复杂度为O(1),但需要较高通信带宽,适用于高延迟网络(广域网)
在恶意敌手模型下, 一系列研究工作也将秘密分享方法 融合到基于混淆电路的常数轮 MPC 协议中以获得更高效率
MPC基础组件
线性秘密分享
( n , t ) (n,t) (n,t)门限线性秘密分享
LSSS主要由三个算法组成:分享算法,重构算法和打开算法
分享算法
[
x
]
←
S
h
a
r
e
(
x
)
[x]\leftarrow Share(x)
[x]←Share(x):
P
i
P_i
Pi获得份额
x
i
x^i
xi,其中共有
n
n
n个参与方
P
1
,
…
,
P
n
P_1,\dots,P_n
P1,…,Pn
重构算法
[
x
]
←
R
e
c
(
x
)
[x]\leftarrow Rec(x)
[x]←Rec(x):
P
i
P_i
Pi获得秘密值
x
x
x(要求至少
t
+
1
t+1
t+1个份额)
打开算法
[
x
]
←
O
p
e
n
(
x
)
[x]\leftarrow Open(x)
[x]←Open(x):所有参与方获得
x
x
x
- 给定 [x] 和 [y], 本地计算 [z] = [x] + [y] 满足 z = x + y.
- 给定 [x] 和公开已知的常数 c ∈ F, 本地计算 [y] = [x] + c 满足 y = x + c.
- 给定 [x] 和公开已知的常数 c ∈ F, 本地计算 [y] = c · [x] 满足 y = c · x.
- 应用于MPC协议设计中,加法等线性们是free(即无需通信)
加法秘密分享
主要用在不诚实大多数MPC协议中(t=n-1)
x
=
x
1
+
x
2
+
⋯
+
x
n
,
x
∈
F
x=x^1+x^2+\dots+x^n,x\in \mathbb{F}
x=x1+x2+⋯+xn,x∈F,其中
x
x
x为秘密(secret),
x
i
x^i
xi为份额(share)
重复秘密分享
主要用在诚实大多数MPC协议中(t<n/2,n较小);以n=3,t=1为例
x
=
x
1
+
x
2
+
⋯
+
x
n
,
x
∈
F
x=x^1+x^2+\dots+x^n,x\in \mathbb{F}
x=x1+x2+⋯+xn,x∈F:
P
1
P_1
P1持有
(
x
2
,
x
3
)
(x^2,x^3)
(x2,x3),
P
2
P_2
P2持有
(
x
1
,
x
3
)
(x^1,x^3)
(x1,x3),
P
3
P_3
P3持有
(
x
1
,
x
2
)
(x^1,x^2)
(x1,x2),
复制秘密分 享主要用在参与方数量 n 比较小的情况, 因为复制秘密分享方案要求每方存储 ( n − 1 t ) \binom{n-1}{t} (tn−1) 个分享
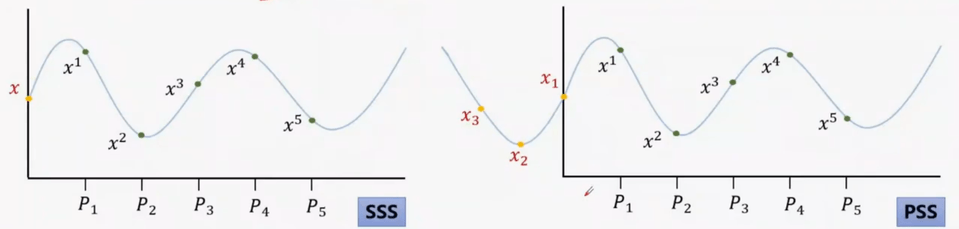
Shamir秘密分享及推广
主要用在诚实大多数MPC协议中(
t
+
1
≤
(
n
+
1
)
/
2
t+1\leq(n+1)/2
t+1≤(n+1)/2)
x
=
f
(
0
)
,
x
i
=
f
(
a
i
)
x=f(0),x^i=f(a_i)
x=f(0),xi=f(ai),其中f为次数t的随机多项式,
α
1
,
…
,
α
n
α
i
∈
F
\alpha_1,\dots,\alpha_n \alpha_i \in \mathbb{F}
α1,…,αnαi∈F为不同的非零域元素
推广形式(打包秘密分享,packed secret sharing):
x
i
=
f
(
β
i
)
,
x
i
=
f
(
a
i
)
,
x_i=f(\beta_i),x^i=f(a_i),
xi=f(βi),xi=f(ai),一个多项式分享k个秘密
x
,
…
,
x
n
x_,\dots,x_n
x,…,xn,其中
β
1
,
…
,
β
k
\beta_1,\dots,\beta_k
β1,…,βk,
α
1
,
…
,
α
n
∈
F
\alpha_1,\dots,\alpha_n\in \mathbb{F}
α1,…,αn∈F为不同的域元素(更小的腐化门限
t
+
k
≤
(
n
+
1
)
/
2
t+k\leq(n+1)/2
t+k≤(n+1)/2)
三种秘密分享的共性
均满足线性性质(加法同态性),均可用于设计高效的MPC协议
三种秘密分享的区别
- 针对恶意敌手,加法秘密分享需要结合信息论消息认证码(IT-MAC)实现秘密的认证,Shamir及重复秘密分享直接保证了秘密的认证(由于大部分实体是诚实的,重构需要t+1/n个分享)
- 重复秘密分享适合于少量参与方(分享尺寸与参与方数量指标成指数关系,例如:3-9个参与方),Shamir秘密分享适合与大量参与方
秘密重构 R e c ( [ x ] , i ) Rec([x],i) Rec([x],i)
P i P_i Pi从安全通道收到 x x x的分享 [ x ] [x] [x](记 [ x ] [x] [x]为秘密 x x x的分享)
- 加法秘密分享: x = ∑ i = 1 n x i x=\sum_{i=1}^{n}x^i x=∑i=1nxi(认证性: 用IT-MAC验证)
- Shamir秘密分享:拉格朗日差值方法计算 x = f ( 0 ) x=f(0) x=f(0)(认证性: 验证所有分享落在多项式f上)
- 重复秘密分享: x = x 1 + x 2 + x 3 x=x^1+x^2+x^3 x=x1+x2+x3(认证性:验证分享的一致性)
信息论消息认证码(IT-MAC)
BDOZ[^bdoz]
SPDZ1
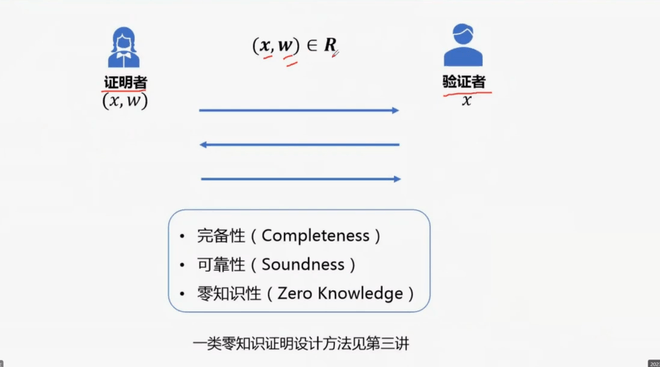
零知识证明
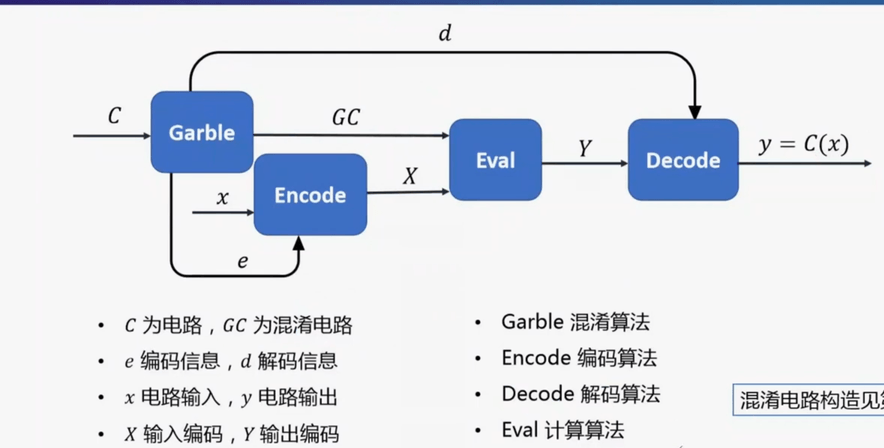
混淆电路
承诺方案
承诺方案是零知识证明协议的关键组件之一。承诺协议将需要被承诺的元素x打包为承诺
C
C
C,还有一个打开算法用于验证
C
C
C和
x
x
x的关系(即
C
C
C由
x
x
x承诺所得)。承诺通常需要具备以下两个性质
(1)隐藏性: 通过承诺C无法得知关于被承诺元素x的任何信息。根据敌手的计算能力又可分为完美隐藏性和计算隐藏性
(2)绑定性: 对与一个承诺
C
C
C,敌手难以找到一个不同于
x
x
x的被承诺元素
x
′
x'
x′,使得打开算法也能通过验证。根据敌手的计算能力又可分为完美绑定性和计算绑定性。
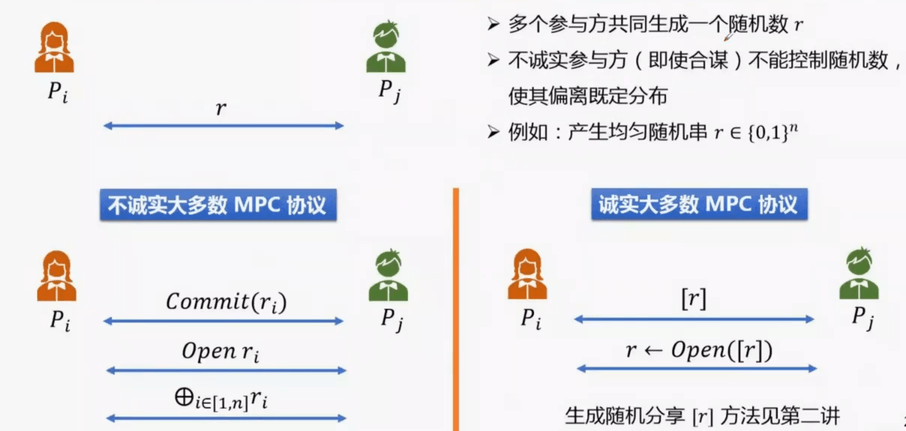
投币(coin-tossing)协议
多个参与方共同生成一个随机数r
不诚实参与方(即使合谋)不能控制随机数,使其偏离既定分布
不诚实发多数MPC协议采用投币协议,诚实大多数MPC协议一般使用秘密分享方案
同态加密(HE)
当前同态加密的分类:
全同态加密(FHE):
f
f
f为任意电路(包括乘法、加法等运算)
层级同态加密(Leveled FHE):
f
f
f为指定深度的任意电路
类同态加密(SHE):
f
f
f为深度浅的任意电路
加法同态加密(AHE):
f
f
f为只包括加法等线性操作的电路
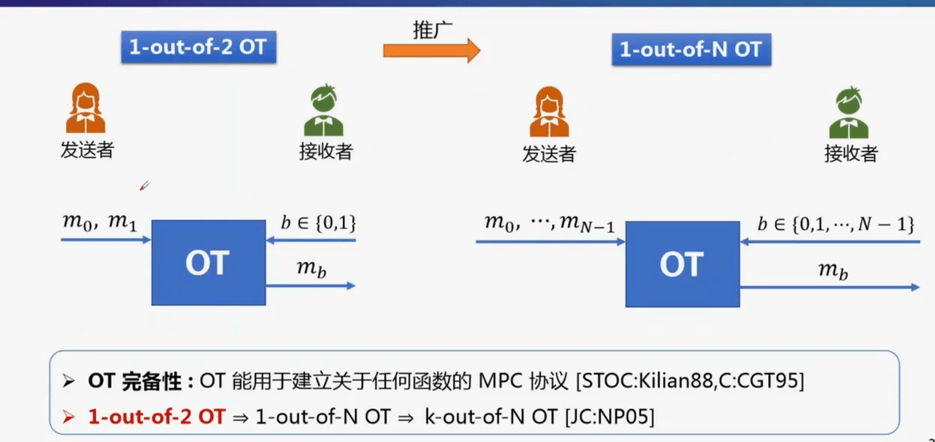
不经意传输及其算术变形
不经意传输协议作为基础密码组件,OT允许发送发 P S P_S PS输入两个消息 m 0 m_0 m0和 m 1 m_1 m1接受方 P R P_R PR输入一个选择比特 b ∈ { 0 , 1 } b\in\{0,1\} b∈{0,1},使得 P R P_R PR仅能获得 m b m_b mb而对 m 1 − b m_{1-b} m1−b完全未知,同时 P S P_S PS不能获得比特 b b b的任何信息。作为OT的一类重要变形,COT要求输入消息 m 0 m_0 m0和 m 1 m_1 m1满足一个固定的相关性 Δ \Delta Δ,即 m 0 ⊕ m 1 = Δ m_0 \oplus m_1=\Delta m0⊕m1=Δ。从向量角度可以这样理解:COT协议输出 ( v , Δ ) (v,\Delta) (v,Δ)给 P S P_S PS,输出 ( w , u ) (w,u) (w,u)给 P R P_R PR,满足 w = v + u ⋅ Δ ∈ { 0 , 1 } k w=v+u\cdot\Delta\in\{0,1\}^k w=v+u⋅Δ∈{0,1}k和 u ∈ { 0 , 1 } u\in\{0,1\} u∈{0,1}
OT依赖于公钥密码组件[c:IR88]
OT能基于不同困难假设构造
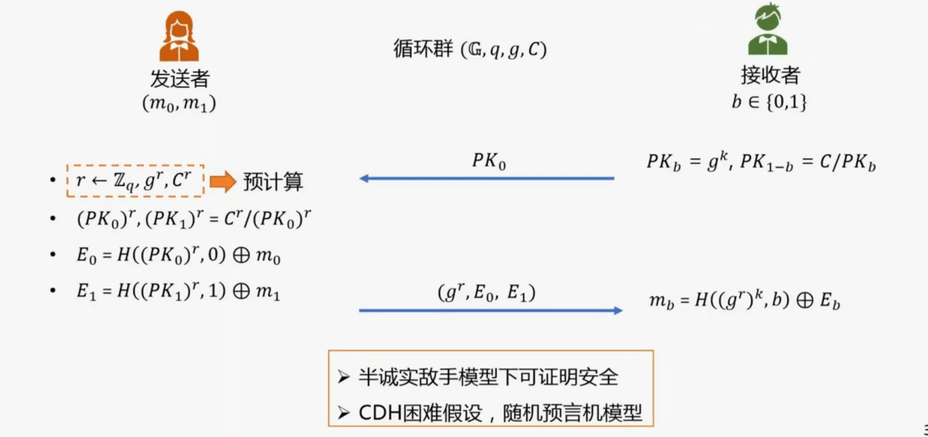
基于OT协议: Naor-Pinkas协议
Naor-Pinkas讲解
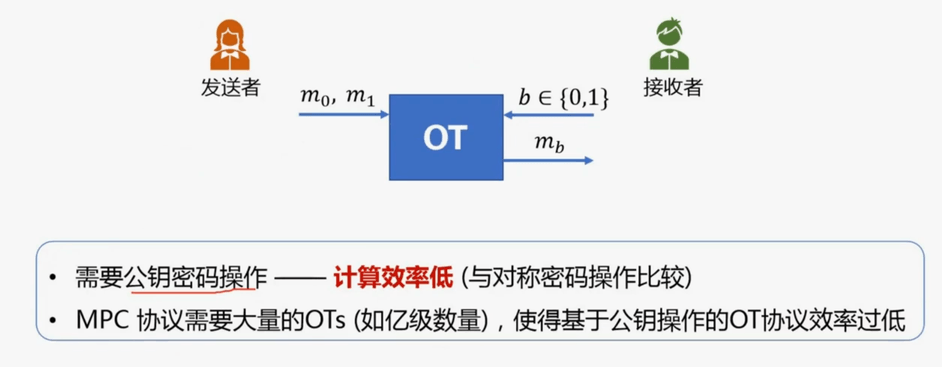
<span注意span> 不经意传输需要公钥密码操作,与堆成密码操作相比,计算效率低,然而MPC协议需要大量的OTs(如亿级数量),使得基于公钥操作的OT协议效率过低
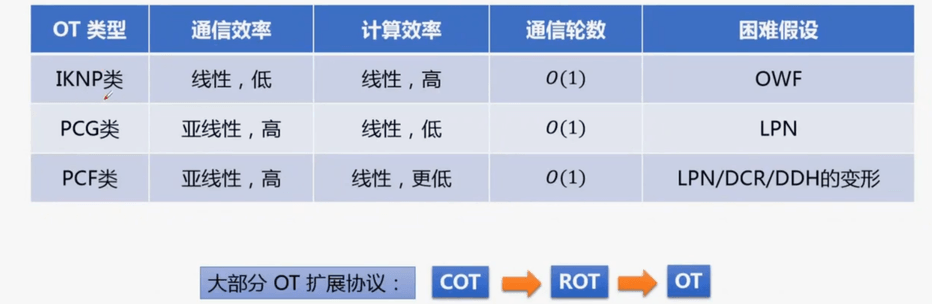
提出不经意传输扩展可用于解决需要大量OTs的问题
名词扫盲
随机预言机
循环群生成元
困难问题LPN/DCR/DDH
参考文献
Multiparty computation from somewhat homomorphic encryption ↩︎