二叉树消消乐

题目描述

给定原始二叉树和参照二叉树(输入的二叉树均为满二叉树，二叉树节点的值范围为[1,1000]，二叉树的深度不超过1000)，现对原始二叉树和参照二叉树中相同层级目值相同的节点进行消除、消除规则为原始叉树和参照二叉树中存在多个值相同的节点只能消除等数量的、消除后的节点变为无效节点，请按节点值出现频率从高到低输出消除后原始二叉树中有效节点的值(如果原始二叉树消除后没有有效节点返回0)。

输入描述

原始二叉树中的节点个数
原始二叉树
参照二叉树中的节点个数
参照二叉树

输出描述

原始二叉树中有效节点的值，按出现频率从高到低排序(相同频率的值按大小排序)，相同频率的值按降序排列。

用例输入

7
1 3 3 3 4 5 6
3
2 3 4

用例输出

36541

样例1解释：
原始二叉树A消除参照二叉树B中的重复元素后，有效节点剩余2个3，1个6，1个5，1个4，1个1，3出现的频率2，6、5、4、1出现的频率为1，按值从大到小排序、所以排序结果为36541。

求解思路

注意审题，题目明确指出这是一个满二叉树，因此我们不需要真的去构建一个二叉树，只需要利用满二叉树的性质去进行模拟求解就行。

需要注意的是，华为的命题人在写题面时候不够严谨，题面说二叉树的深度不超过1000，这显然是不现实的，毕竟这是满二叉树，如果深度达到几十上百的话，二叉树的节点数直接2的几百次方，显然这么大的数据哪怕O(n)的时间复杂度也过不了。因此只需要按照节点数为1e5的规模来设计算法即可。

#include<bits/stdc++.h>
using namespace std;
const int maxn = 100001;
int n, m;
int origin[maxn], refer[maxn];
vector<int>sum(maxn, 0);

void dfs(int depth) {
    int start = pow(2, depth - 1), end = start + pow(2, depth - 1);
    if(start > n || start > m) return;
    map<int, int>mp1, mp2;
    for(int i = start; i < end; i++) {
        mp1[origin[i]]++;
        mp2[refer[i]]++;
    }
    for(auto i : mp1) {
        if(mp2[i.first] > i.second) sum[i.first] -= i.second;
        else sum[i.first] -= mp2[i.first];
        // cout << i.first << " " << sum[i.first] << endl;
    }
    dfs(depth + 1);
}

bool cmp(pair<int, int>a, pair<int, int> b) {
    if(a.second != b.second) return a.second > b.second;
    return a.first > b.first;
}

int main() {
    scanf("%d", &n);
    for(int i = 1; i <= n; i++) {
        scanf("%d", &origin[i]);
        sum[origin[i]]++;
    }
    scanf("%d", &m);
    for(int i = 1; i <= m; i++) scanf("%d", &refer[i]);

    dfs(1);

    // for(int i = 1; i <= n; i++) cout << sum[origin[i]] << " ";
    // cout << endl;

    vector<pair<int, int>>v;
    set<int>s;
    for(int i = 1; i <= n; i++) s.insert(origin[i]);
    for(auto i : s) v.push_back(make_pair(i, sum[i]));

    // for(auto i : s) cout << i << " " << sum[i] << " " << endl;

    sort(v.begin(), v.end(), cmp);
    bool flag = false;
    for(auto i : v) {
        if(i.second != 0) {
            flag = true;
            printf("%d", i.first);
        } 
        else break;
    }
    if(!flag) printf("0");

    return 0;
}
/*
15
5 8 8 8 7 7 7 6 6 9 9 7 7 5 6
7
5 6 6 7 7 8 8
*/

好友推荐系统

题目描述

你正在为一个社交网络平台开发好友推荐功能。

平台上有N个用户(每个用户使用1到N的整数编号)，同时系统中维护了用户之间的好友关系。

为了推荐新朋友，平台决定采用“共同好友数量"作为衡量两个用户之间相似度的标准。

系统根据输入用户编号K，输出与此用户K相似度最高的前L个用户ID来推荐给用户K。

相似度定义:两个用户非好友，两个用户的相似度为拥有的共同好友数(例如用户A和用户B，只有共同好友C和D，相似度=2)

输入描述

第一行包含四个整数 N，M 、K和L，分别表示用户的数量(N)，好友记录条数(M)、查询的用户编号(K)和推荐的好友数量(L)。接下来 M 行，每行包含两个整数编号X和Y，表示编号为X和Y用户是好友。

1. 输入格式都是标准的，无需考虑输出异常场景(不会包含用户和自己是好友的输入，例如11)

2. 用户数不超过1024，用户编码最大1024

3. 好友记录数不超过10240

输出描述

根据输入K和L，输出和用户K相似度最高的L个用户编码。

1. 输出相似度最高的前L个用户编码，按照相似度从高到低排序

2. 如果有相似度相同的可能好友，按照用户编号从小到大排序

3. 如果推荐的好友个效不足L个，则推荐与用户K无无共同好友关系的用户(陌生人)作为可能好友，如果推荐仍不满足L个用户，剩余推荐用户编码使用0来占位

用例输入

6 7 3 2
1 2
1 3
2 3
3 4
3 5
4 5
5 6

用例输出

6 0

输入包含了6个用户，7条好友记录，给用户ID编号为3的用户推荐2个好友。

输出只有编号为6的用户可能是编号3用户的可能好友;

尝试推荐与编号3用户无共同好友的其他用户，由于除编号为6的用户之外，其他用户和编号3用户都是好友，所以找不到陌生人作为推荐的第二个用户;

推荐结果不足2个用户，所以推荐的第二个用户编码使用0来占位补足。

求解思路

我们首先可以利用哈希表构建用户之间的好友关系，方便在O(1)的时间复杂度内查找两个用户之间是否是好友关系

然后排序遍历就可以得到推荐列表了

#include<bits/stdc++.h>
using namespace std;
bool cmp(pair<int, int> a, pair<int, int> b) {
    if(a.second != b.second) return a.second > b.second;
    return a.first < b.first;
}
int main() {
    int N, M, K, L;
    scanf("%d %d %d %d", &N, &M, &K, &L);
    int x, y;
    int isf[1025][1025] = {0};
    for(int i = 0; i < M; i++) {
        scanf("%d%d", &x, &y);
        isf[x][y] = isf[y][x] = 1;
    }

    vector < pair<int, int> > sim;

    for(int i = 1; i <= N; i++) {
        if(i == K) continue;
        if(isf[K][i] != 1) {
            int cnt = 0;
            for(int j = 1; j <= N; j++) {
                if(i == j) continue;
                if(isf[K][j] == 1 && isf[i][j] == 1) cnt++;
            }
            sim.push_back(make_pair(i, cnt));
        }
    }

    sort(sim.begin(), sim.end(), cmp);
    int sum = 0;
    for(auto i : sim) {
        printf("%d ", i.first);
        sum++;
    }
    if(sum < L) {
        for(int i = sum; i < L; i++) printf("0 ");
    }

    return 0;
}

维修工

题目描述

维修工要给n个客户更换设备，为每个用户更换一个设备。维修工背包内最多装k个设备，如果背包里有设备可以直接前往下一个客户更换或回公司补充设备，没有则需要回公司取设备。这些客户有优先级，维修工需要按照优先级给客户更换设备，优先级level用数字表示，数字小的优先级高。维修工从公司出发，给n个客户更换设备，最后再返回公司。请计算维修工完成这项工作所需要经历的最短总距离是多少。维修工可以走斜线。

输入描述

第一行两个正整数 n,k(1≤k≤n≤2000),表示客户数和维修工背包容量。
第二行两个正整数 x,y ，用空格分隔(1 ≤ x , y ≤ 10^6),表示公司的坐标
接下来n行每行三个正整数 $x_i$, $y_i$, $leve{l}_i$，用空格分隔(1≤$x_i$,$y_i$≤10^6,1≤$leve{l}_i$<=n)。
($x_i$, $y_i$)表示第i个客户的位置坐标，$leve{l}_i$表示第$i$个客户的优先级，保证所有客户优先级不同，客户和公司坐标不会重叠。

输出描述

输出最短总距离，结果四舍五入并保留一位小数，例如:9.0。

用例输入

3 2
1 1
3 1 1
1 2 2
3 2 3

用例输出

9.2

样例1解释：

从(1,1)->(3,1)->(1,1)->(1,2)->(3,2)->(1,1) = 2+2+1+2+√5 = 9.236

求解思路

题目的意思是维修工在维修完一家客户后，就会废掉背包内的一个设备（题面没讲清楚，一开始理解了好久背包内有设备为什么需要回公司取）。

因为本题规定了客户的优先级，因此我们首先将客户按照优先级进行排序。

接下来，我们可以按照记忆化搜索的方法，决定维修完当前客户后，到底回公司取设备再前往下一家客户还是直接去下一家客户维修。

我们采用memo数组记录每次的结果

memo[i + 1][k - 1] 表示回公司取完设备再前往下一家客户维修

memo[i + 1][j - 1] 表示背包内还有设备，直接前往下一家客户维修

#include<bits/stdc++.h>
using namespace std;

double cal_dis(int x1, int y1, int x2, int y2) {
    return (double)sqrt(pow(x1 - x2, 2) + pow(y1 - y2, 2));
}

const int maxn = 2001;
int n, k, cx, cy;

struct customer
{
    int x, y, level;
    bool operator < (const customer& other) const { 
        return level < other.level; 
    }
}p[maxn];

/*
记忆化搜索，假设memo[i][j]表示维修完第i个客户，并且背包中还剩下j个设备。
*/
vector <vector<double>> memo(maxn, vector<double>(maxn, 0)); 

double dfs(int i, int j) {
    if(memo[i][j] > 0) return memo[i][j];
    double dis = cal_dis(p[i].x, p[i].y, cx, cy);
    double ans = 99999999999.0;
    if(i < n - 1) {
        ans = min(ans, dfs(i + 1, k - 1) + dis + cal_dis(p[i + 1]. x, p[i + 1].y, cx, cy));
        // cout << dis + cal_dis(p[i + 1]. x, p[i + 1].y, cx, cy) << endl;
        if(j > 0) {
            ans = min(ans, dfs(i + 1, j - 1) + cal_dis(p[i + 1].x, p[i + 1].y, p[i].x, p[i].y));
            // cout <<  cal_dis(p[i + 1].x, p[i + 1].y, p[i].x, p[i].y) << endl;
        }
    } else { // 如果是最后一家，则修完直接回公司
        ans = dis;
    }
    return memo[i][j] = ans;
}

int main() {
    scanf("%d%d", &n, &k);
    scanf("%d%d", &cx, &cy);
    for(int i = 0; i < n; i++) scanf("%d%d%d", &p[i].x, &p[i].y, &p[i].level);
    sort(p, p + n);

    dfs(0, k);

    double ans = dfs(0, k - 1) + cal_dis(p[0].x, p[0].y, cx, cy);
    printf("%.1f", ans);

    return 0;
}

维修工这个题是通过记忆化搜索求解最短路径的问题，想起之前在力扣上面刷到一个类似的题目，K站中转内最便宜的航班

题目链接

力扣上类似的题–K站中转内最便宜的航班

题目描述

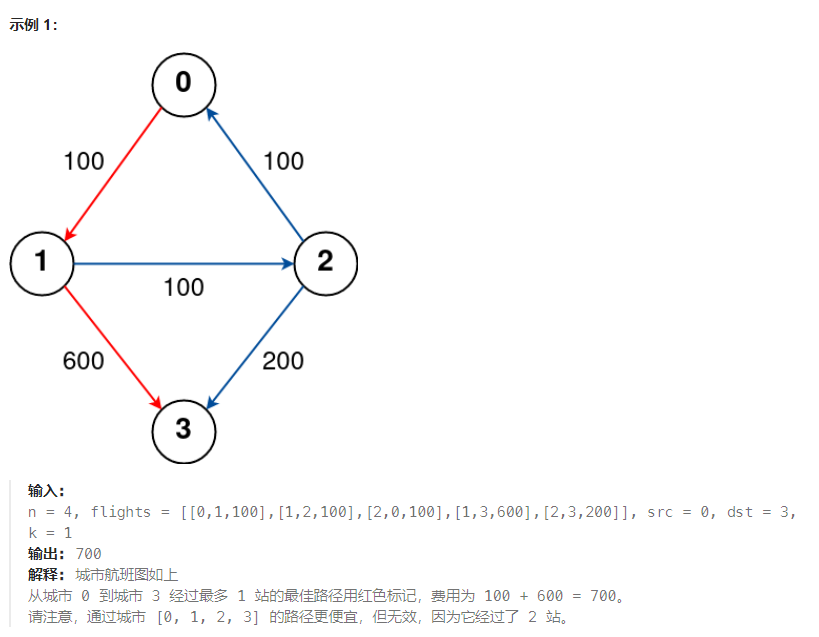
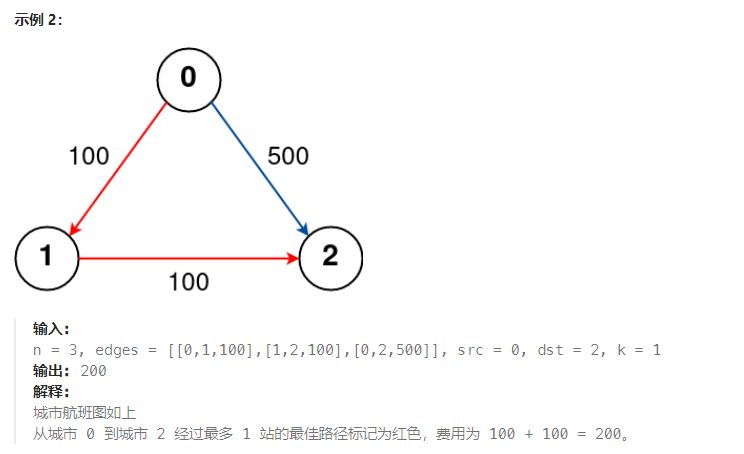
有 n 个城市通过一些航班连接。给你一个数组 flights ，其中 flights[i] = [fromi, toi, pricei] ，表示该航班都从城市 fromi 开始，以价格 pricei 抵达 toi。

现在给定所有的城市和航班，以及出发城市 src 和目的地 dst，你的任务是找到出一条最多经过 k 站中转的路线，使得从 src 到 dst 的 价格最便宜 ，并返回该价格。 如果不存在这样的路线，则输出 -1。

求解思路

和维修工一样，我们只需要利用记忆化搜索去寻找到第k个城市所需要的最少花费即可，注意k次中转的限制。

class Solution {
public:
    const int INF = 99999999;
    /*
    dp[i][j] 表示起点到城市i到达第j个城市的最少花费
    */
    int findCheapestPrice(int n, vector<vector<int>>& flights, int src, int dst, int k) {
        vector <int> G[n]; // 构建邻接矩阵
        vector <vector<int>> price(n, vector<int>(n, INF));
        for(auto flight : flights) {
            G[flight[0]].push_back(flight[1]); 
            price[flight[0]][flight[1]] = flight[2];
        }

        vector <vector<int>> dp(n, vector<int>(k + 2, 0));

        function<int(int, int)> dfs = [&](int i, int j) {
            if(dp[i][j] > 0) return dp[i][j];
            if(i == dst) {
                if(j <= k + 1) return dp[i][j];
                return INF;
            }
            int ans = INF;
            for(auto v : G[i]) {
                if(j < k + 1)
                    ans = min(ans, dfs(v, j + 1) + price[i][v]);
            }
            return dp[i][j] = ans;
        };

        int ans = dfs(src, 0);
        return ans == INF ? -1 : ans;
    }
};