Java实现七大排序（二）

一.交换排序

1.冒泡排序

这个太经典了，每个学编程都绕不开的。原理跟选择排序差不多，不过冒泡排序是直接交换。

   public static void bubbleSort(int[] array){
        for (int i = 0; i < array.length - 1; i++) {
            for (int j = 0; j < array.length-1-i; j++) {
                if(array[j]>array[j+1]){
                    swap(array,j,j+1);
                }
            }
        }
    }

这个已经是优化过的版本了，当然这个代码还可以再进行优化。优化思路：当 i 后面的元素全部有序后就不进行排序了直接退出循环。

public static void bubbleSortOptimize(int[] array){
        for (int i = 0; i < array.length - 1; i++) {
            boolean flg = false;
            for (int j = 0; j < array.length-1-i; j++) {
                if(array[j] > array[j+1]) {
                    swap(array,j,j+1);
                    flg = true;
                }
            }
            if(!flg) {
                break;
            }
        }
    }

2.快速排序（重要）

快速排序是 Hoare 于1962年提出的一种二叉树结构的交换排序方法，其基本思想为：任取待排序元素序列中的某元素作为基准值，按照该排序码将待排序集合分割成两子序列，左子序列中所有元素均小于基准值，右子序列中所有元素均大于基准值，然后最左右子序列重复该过程，直到所有元素都排列在相应位置上为止。

简短的说，从序列挑一个元素作为基准，让比基准元素小的元素放在该元素的左面，比它大的元素放在右面。再把基准元素右面的看作一组，左面看作一组，在进行刚刚的操作，直到某一组只有一个元素的时候停止。

public static void quickSort(int[] arr,int left,int right){
        if(left>=right){
            return ;
        }

        int l=left;
        int r=right;

        int cur=arr[left];

        while(left<right){

            while(left<right && arr[right]>=cur){
                right--;
            }
            arr[left]=arr[right];
            while(left<right && arr[left]<=cur){
                left++;
            }
            arr[right]=arr[left];
        }
        arr[left]=cur;

        quickSort(arr,l,left-1);
        quickSort(arr,left+1,r);
    }

这个是以左端点为基准，右端点、中间点等都可以作为基准，序列任何没被当过基准点都可以当基准点。

这个是以中间点为基准的：

public static void quickSort(int[] array,int left,int right){
            if(left >= right){
                return ;
            }
            //x为基准
            int x = array[(left+right)/2];
            int i = left - 1;
            int j = right + 1;

            while(i < j){
                do{
                    i ++ ;
                }while (array[i] < x);
                
                do {
                    j--;
                }while (array[j] > x);
                
                if(i < j){
                    swap(array,i,j);
                }
            }

            quickSort(array, left, j);
            quickSort(array, j + 1, right);
    }

前后两个引用指向，前面的先走，找到第一个比基准大的数停下；后面的走，找到第一个比基准小的数停下，将两个指向的值交换。继续重复上面的步骤，直到两个指向相遇。相遇时保证了基准左面都比基准小，右面都比基准大。

二.归并排序

采用分治法，先将序列分解，再将已有序的子序列合并，最终得到全部元素有序。若将两个有序表合并成一个有序表，称为二路归并。

public static void mergeSort(int[] array,int left,int right){
        if(left>=right){
            //终止条件
            return ;
        }

        //分解
        int mid=(left+right)/2;
        mergeSort(array,left,mid);
        mergeSort(array,mid+1,right);

        //合并
        int[] tem=new int[right-left+1];
        int k=0;
        int s1=left,e1=mid;
        int s2=mid+1,e2=right;

        while(s1<=e1 && s2<=e2){
            if(array[s1]>array[s2]){
                tem[k++]=array[s2++];
            }else{
                tem[k++]=array[s1++];
            }
        }
        
        //把剩下没有遍历到的放入临时数组
        while(s1<=e1){
            tem[k++]=array[s1++];
        }
        while(s2<=e2){
            tem[k++]=array[s2++];
        }

        for (int i = 0; i < k; i++) {
            array[i+left]=tem[i];
        }
    }

三.总结

排序方法	最好	平均	最坏	空间复杂度	稳定性
冒泡排序	O(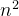 $n^{2}$ )	O( $n^{2}$ )	O( $n^{2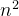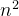}$ )	O(1)	稳定
快速排序	O(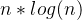)	O(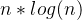)	O(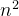 $n^{2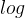}$ )	O((n))~O()	不稳定
归并排序	O(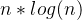)	O(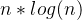)	O(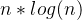)	O()	稳定