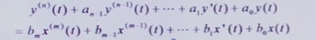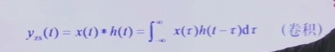线性时不变系统描述
连续系统:
连续系统由线性常系数微分方程描述
特性:
输入为x(t),输出y(t)
则,输入为x(t)的线性变化,积分,微分时,输出也对应的变化。
离散系统:
一般使用 线性常系数差分方程描述
利用离散系统可以也进行滤波等处理
特性:
具有差分特性 、 求和特性
LTI响应的时域分析
求响应目的:建立起输入输出系统之间的关系。
求响应的方法:
- 求解微分方程(纯数学)(局限性)
- 求解零输入响应和零状态响应(重点介绍)
求解微分方程的方法
先求特解,再通过输入求通解(包括通解的系数,也要通过把通解带入方程的方法求出来),再通过初值求C。
缺点:如果输入/初始条件 发生变化,需要重新求解,而且只能求解输入比较简单时的响应
通过零输入响应和零状态响应
完全响应 = 零输入响应zi+零状态响应zs
零输入响应就是微分方程右边为 0
零状态响应求法:
- 将输入信号表示为 单位冲激信号的线性组合
- 求出单位冲激信号的冲激响应h(t)
- 求零状态响应yzs(t)
可以推导出以下公式:
yzs(t) = x(t) * h(t) //卷积
零输入响应的求解
- 求微分方程特征
- 求零输入响应形式
- 将初始状态代入
系统的冲激响应求解
系统在初始状态为0的条件下,冲激信号δ(t)输入系统的响应,表示为h(t)。
求法:
把微分方程中的输入替换为δ(t),输出替换为h(t).
零状态响应
h(t)是一个信号,可以用来描述系统,冲激响应只和系统有关,是一个描述系统时域特性的函数,注意这种描述方法。
yzs(t) = x(t) * h(t)=∫x(T)h(t-T)dT //卷积
这个公式把输入输出系统联系了起来
卷积怎么求:
方法1:解析法(要求知道两个函数的表达式)
例题:
方法2: 图形法
将其中一个函数翻转,从左到右平移,每平移到一个新阶段,计算积分
卷积的结果是一个新的信号,卷积的起点等于两个信号的起点之和,终点时两个信号终点之和。
两个矩形做卷积,结果时等腰梯形,上底为差,下第为和。
方法3: 利用性质
卷积的性质:
交换律:交换
分配律:展开相加
结合律:后面的先乘也可以
等效特性:两个函数分别卷积和积分,得到的结果不变
平移特性:
x(t)*δ(t-T) = x(t-T)
x1(t-t1) * x2(t-t2) = y(t-t1-t2)
微分特性:和δ(t)的微分做卷积,结果是函数的微分
积分特性:和u(t)做卷积,结果是函数的积分
冲激响应表示系统的特性
冲激响应有两层含义:
- 一个冲击信号作用于系统后,系统的输出
- 对系统的描述
系统级联/并联
级联:前一个系统的输出,是下一个系统的输入。
y(t) = x(t) * h1(t) * h2(t)
并联:
y(t) = x(t) * (h1(t) +h2(t))
判断系统因果性
因果系统: 输出之后于输入。
一个线性时不变系统,如果h(t) =0,t< 0,就是因果系统。
(因为卷积的性质:卷积结果的起点时两个函数的起点之和,其中一个起点大于0,那么和肯定大于输入。)
判断系统稳定系统
定义: 对任意的有界输入,输出也有界,就是稳定系统。
连续LTI系统,稳定的充分必要条件:
∫|h(t)|dt = S <+∞
有了冲激响应,就可以分析系统的特性了。