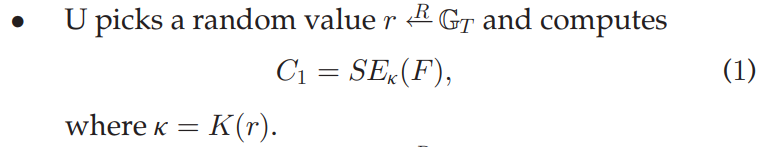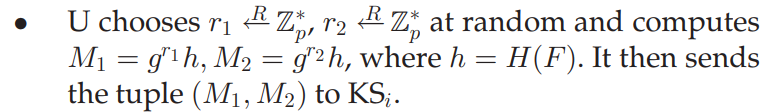charm的github位置 JHUISI/charm: Charm: A Framework for Rapidly Prototyping Cryptosystems

简单介绍

这是在github上的介绍。
Charm is a framework for rapidly prototyping advanced cryptosystems. Based on the Python language, it was designed from the ground up to minimize development time and code complexity while promoting the reuse of components.

因为提供python接口，charm可以很方便地实现各种密码算法，尤其是复现论文中提出的相关算法。当然比较经典的算法它的schemes中也集成了。

安装

JHUISI/charm: Charm: A Framework for Rapidly Prototyping Cryptosystems
Charm-crypto的安装以及简单实现的聚合签名算法_ganhuoganhuo的博客-CSDN博客_charm-crypto
Charm-crypto的安装与使用_YangPotatoes的博客-CSDN博客_charm-crypto
如果进行到 make test，并且成功，那么就说明安装成功了。
make test (may also require super-user privileges)

本地环境：Ubuntu18 + Python 3.6.9

使用

官方文档 Charm-Crypto Docs! — Charm-Crypto 0.50 documentation
但其实有时候直接看源码更加方便

schemes

schemes

• abenc (Attribute-Based Encryption) 属性基加密
• commit (Commitment Scheme)
• grpsig (Group Signature) 群签名
• hibenc (Hierarchical Identity Based Encryption)
• ibenc (Identity Based Encryption) 基于身份加密
• pkenc (Public Key Encryption) 公钥加密
• pksig (Public Key Signature ) 公钥签名
• prenc (Proxy Re Encryption) 代理重加密

以代理重加密的部分算法为例。如下图，pre_afgh06，pre是代理重加密，afgh是算法缩写（发明人的首字母合在一起），06是2006年。pre_bss98是1998年的。

打开代码可以看到具体的信息，如算法出自的论文，并且最上面就是它所属的类别。如这里的Proxy Re-Encryption。

文档对应部分 Implemented Schemes
schemes的导入，可以根据文档目录来导入，当然直接导入类也可以。
from charm.schemes.pkenc import pkenc_elgamal85

pair

charm的pair是基于PBC库的。具体的使用因为我对密码也不是特别了解，便不再班门弄斧。但对于较新的算法，可以参考经典的算法，依葫芦画瓢大致也能写出。

这里补充一些可能用到的函数。PairingGroup类可以进行序列化，这样方便存储。

from charm.toolbox.pairinggroup import PairingGroup,ZR,G1,G2,GT,pair
p = PairingGroup('SS512')
v1 = p.random(G1)
b1 = p.serialize(v1)
print(b1, type(b1))
print(v1 == p.deserialize(b1))

运行结果如下

charm/pairinggroup.py at dev · JHUISI/charm

对称加密

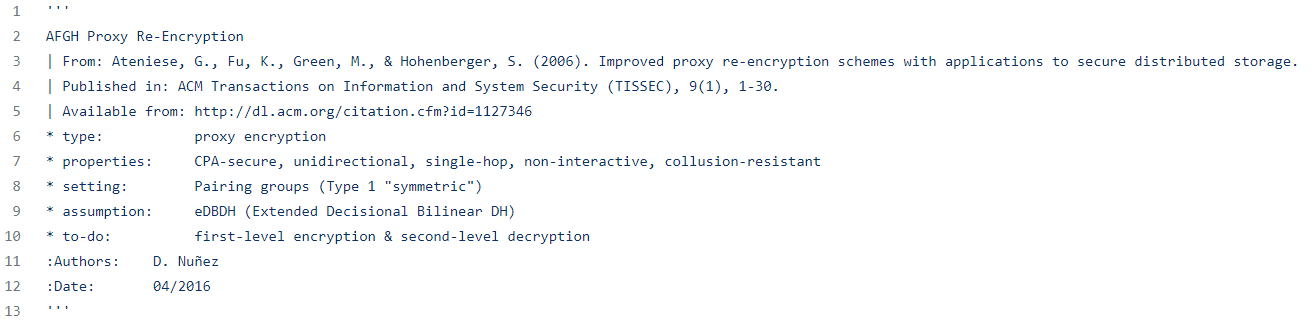
在编写算法时，经常要利用椭圆曲线上的点生成数据密钥。而我们常用的crypto库提供的对称加密算法都是利用bytes类型作为密钥，这样就极不方便。
以PAERP “Decentralized Server-Aided Encryption for Secure Deduplication in Cloud Storage” 为例。在其中有这样的一个步骤。

$S{E}_{\kappa }$ 是以 $\kappa$ 为数据密钥对称加密，而 $\kappa =K(r)$。我们看到 $r$ 是随机生成的，但它属于 ${\mathbb{G}}_T$。但 ${\mathbb{G}}_T$是PairingGroup类型。实现这个步骤就是我们接下来研究的东西。

from charm.toolbox.pairinggroup import PairingGroup,ZR,G1,G2,GT,pair,extract_key
from charm.toolbox.symcrypto import SymmetricCryptoAbstraction

def symmetric_encrypt(msg, dk):
    '''
    dk data key.
    '''
    k = extract_key(dk)
    a = SymmetricCryptoAbstraction(k)
    c = a.encrypt(msg)
    return c
    
def symmetric_decrypt(cipher, dk):
    k = extract_key(dk)
    a = SymmetricCryptoAbstraction(k)
    msg = a.decrypt(cipher)
    return msg  

group = PairingGroup('SS512')
msg = 'bird fly in the sky.'
dk = group.random(GT)
cipher = symmetric_encrypt(msg, dk)
print(cipher)
print(symmetric_decrypt(cipher, dk).decode('utf-8') == msg)

运行结果如下

默认是 AES, CBC模式。关于其中的extract_key 代码中有这样的描述。

A large number of the schemes can only encrypt group elements and do not provide an efficient mechanism for encoding byte in those elements. As such we don’t pick a symmetric key and encrypt it asymmetrically. Rather, we hash a random group element to get the symmetric key.

charm/symcrypto.py at dev · JHUISI/charm

Shin Y, Koo D, Yun J, et al. Decentralized server-aided encryption for secure deduplication in cloud storage[J]. IEEE Transactions on Services Computing, 2017.

哈希 hash

同样以上篇论文为例，在其中一个步骤中，涉及到将文件转换为pair类型。可以看到$h=H(F)$，$F$就是file，$H$就是hash，可以看到$M_1=g^{r_1}h$，$h$要想在这之中计算，不得不转换为相同的类型。而接下来我们就是解决这个问题。

from charm.toolbox.pairinggroup import PairingGroup,ZR,G1,G2,GT,pair,extract_key

group = PairingGroup('SS512')
data = 'bird fly in the sky.'
h = group.hash(data, G1)
print(type(h), h)

运行结果如下

charm/pairinggroup.py at dev · JHUISI/charm