梯度消失(Vanishing Gradient)问题是深度神经网络训练中的一个关键问题,它主要发生在反向传播过程中,导致靠近输入层的权重更新变得非常缓慢甚至几乎停滞,严重影响网络的训练效果和性能。
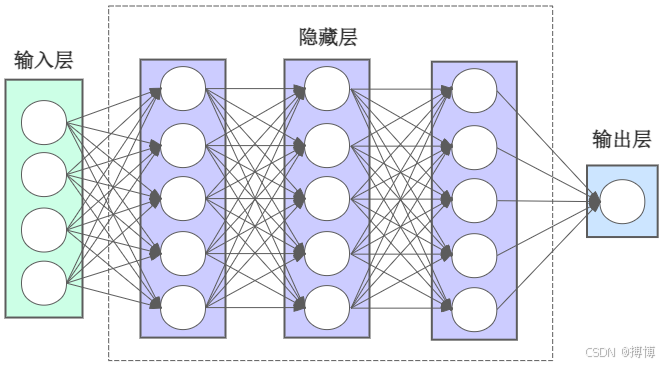
图1 在深度神经网络中容易出现梯度消失和梯度爆炸问题
超过三层以上的神经网络称为深度神经网络。
一、定义与现象
梯度消失是指在深度神经网络的反向传播过程中,随着网络层数的增加,梯度值逐层减小,最终趋近于零。这会导致靠近输入层的隐藏层权重更新变得非常缓慢,几乎不更新,从而阻止网络从输入数据中学习有效的特征表示。
二、先了解几个基本概念和反向传播过程
1. 几个基本概念
(1)前向传播:数据从输入层开始,经过隐藏层,最终到达输出层的过程。在这个过程中,每一层的输入都是前一层的输出,而每一层的输出则作为下一层的输入。
(2)损失函数:用于量化模型预测值与实际值之间的差异。常见的损失函数包括均方误差、交叉熵损失等。
(3)梯度:损失函数相对于网络参数的偏导数,表示了损失函数在该点处相对于参数的变化率。
2. 反向传播步骤
(1)计算输出层的误差:根据损失函数,计算输出层的预测值与实际值之间的差异,得到输出层的误差。
(2)逐层反向传播误差:从输出层开始,使用链式法则逐层计算每个隐藏层的误差。链式法则允许我们将输出层的误差反向传播到每一层,并计算每层的梯度。对于每一层,我们计算该层每个神经元的梯度,这个梯度表示了损失函数相对于该神经元权重的偏导数。
(3)更新网络参数:使用计算得到的梯度,根据梯度下降算法或其他优化算法,更新网络的权重和偏置。梯度下降算法的更新公式为:new_parameter = old_parameter - learning_rate * gradient,其中learning_rate是学习率,用于控制更新的步长。
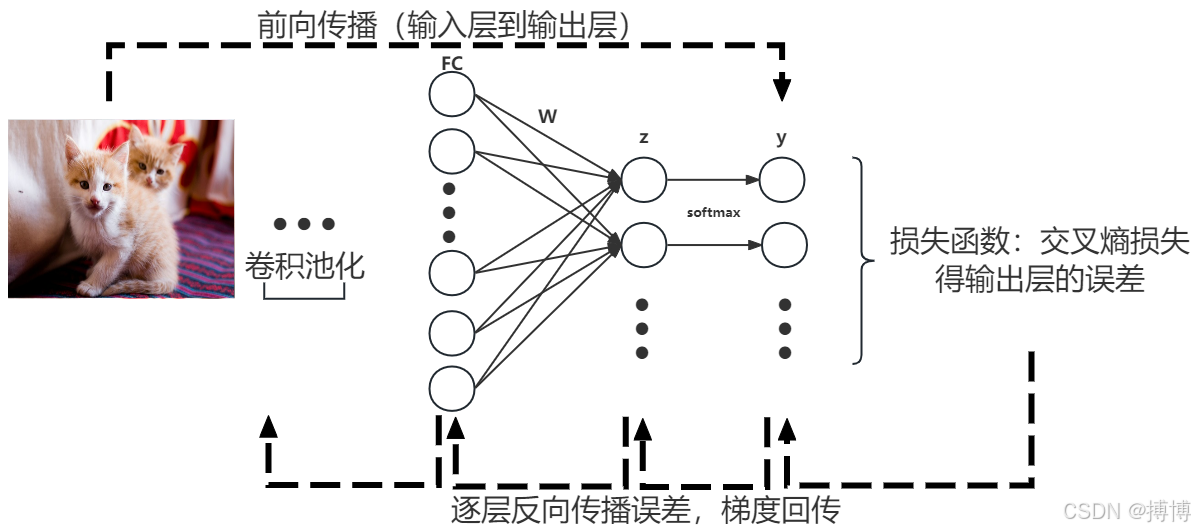
图2 深度神经网络的反向传播过程
三、原因
梯度消失问题主要由以下几个因素引起:
1. 激活函数的选择:某些非线性激活函数(如Sigmoid和Tanh)在输入值非常大或非常小时,其导数(或梯度)会趋近于零。在深度神经网络中,这些激活函数的梯度在反向传播过程中会逐层累积减小,最终导致梯度消失。
经过神经网络中多层的变换,很可能使得后面层的输入数据变得过大或过小,从而掉进激活函数(例如Sigmoid、Tanh)的饱和区。
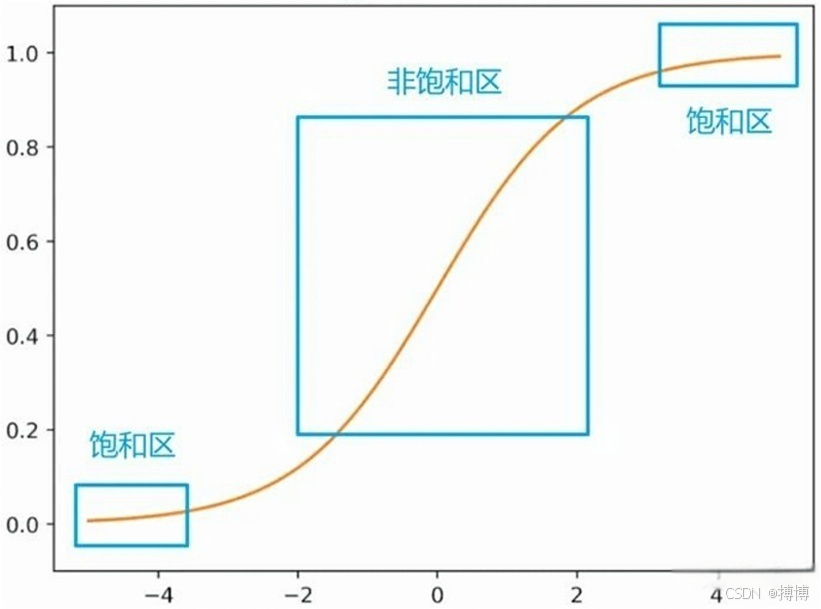
图3 Sigmoid函数存在梯度消失问题
饱和区的梯度随x的变化y的变化很不明显,即会产生梯度消失问题,进而导致学习过程停止。为防止这个问题,我们希望,数据落入激活函数中间的非饱和区。为了降低内部协变量偏移所带来的负面影响,在训练过程中一般会采用非饱和型激活函数(ReLU)、精细的网络参数初始化,保守的学习率,但这不仅会使得网络的学习速度太慢,还会使得最终效果特别依赖于网络的初始化。
2. 链式法则的应用:在深度神经网络中,梯度是通过链式法则从输出层逐层反向传播到输入层的。每一层的梯度都是前一层梯度与该层激活函数导数的乘积。如果每一层的梯度都稍微减小一点,那么经过多层传播后,梯度值就会变得非常小,几乎为零。
3. 权重初始化不当:如果网络权重的初始值设置得太小,那么在前向传播过程中,输入信号可能会迅速衰减,导致激活函数的输入值非常小,进而使得梯度在反向传播过程中也迅速减小。
4. 网络层数过多:随着网络层数的增加,梯度需要通过更多的层进行反向传播。每一层都可能对梯度进行一定的衰减,因此层数越多,梯度消失的风险就越大。
四、影响
梯度消失问题对深度神经网络的训练效果和性能有着显著的影响。由于靠近输入层的权重更新变得非常缓慢甚至几乎停滞,这会导致网络无法从输入数据中学习有效的特征表示,从而降低模型的准确性和泛化能力。
五、解决方法
为了解决梯度消失问题,可以采取以下措施:
1. 选择合适的激活函数:使用ReLU及其变体(如Leaky ReLU、Parametric ReLU等)作为激活函数。这些激活函数在输入为正时具有恒定的导数(对于ReLU为1),有助于缓解梯度消失问题。同时,它们还具有计算简单、收敛速度快等优点。
合理的权重初始化:采用合适的权重初始化方法(如He初始化或Glorot初始化)来设置网络权重的初始值。这些方法可以根据网络的层数和激活函数的特点来设置权重的初始值,从而减小梯度消失的风险。
2. 引入批量归一化(Batch Normalization):在每一层的输入处进行归一化操作,使每一层的输入分布更加稳定。这有助于减小内部协变量偏移(Internal Covariate Shift)问题,提高模型的收敛速度和稳定性,同时也在一定程度上缓解梯度消失问题。
3. 使用残差连接(Residual Connections):通过引入残差连接来构建残差网络(Residual Networks, ResNets)。残差连接允许梯度在反向传播时直接跳过某些层,从而缓解梯度消失的现象。这种方法在深度神经网络中非常有效,可以显著提高模型的训练效果和性能。
4. 调整优化算法参数:合理设置优化算法的学习率、动量等参数。学习率不宜过大也不宜过小,以避免权重更新过快或过慢而导致的梯度消失或梯度爆炸问题。动量参数可以帮助稳定梯度更新过程,提高训练的稳定性。