多目标优化策略之一：非支配排序

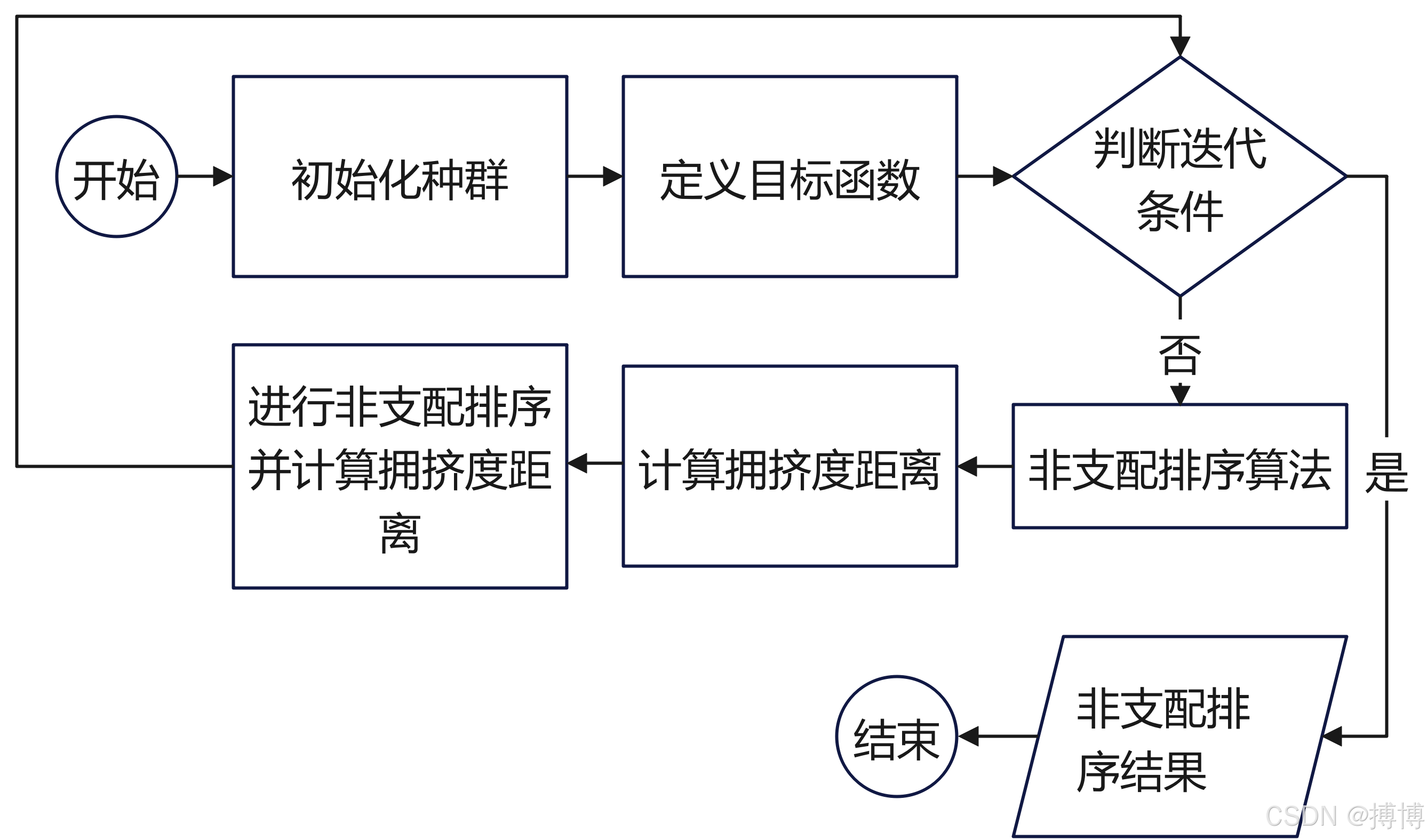
多目标优化策略中的非支配排序是一种关键的技术，它主要用于解决多目标优化问题中解的选择和排序问题，确定解集中的非支配解（也称为Pareto解）。

关于什么是多目标优化问题，可以查看我的文章：改进候鸟优化算法之五：基于多目标优化的候鸟优化算法（MBO-MO）-CSDN博客

图1 非支配排序的思维导航图

一、非支配排序的基本概念

（1）非支配解（Pareto解）：如果一个解不被解集中的其他任何解所支配，则该解被称为非支配解（或不受支配解），也称Pareto解。假设有两个解S1和S2，如果S1在所有目标函数上都不比S2差，并且至少在一个目标函数上严格优于S2，则称S1支配S2，此时S1为非支配解。

（2）支配关系：若解S2在所有目标函数上均劣于S1，则称S1优于S2，也称S1支配S2，S2为受支配解。数学上，可以表达为S1⪯S2（注意，这里的符号“⪯”表示支配关系）。

（3）Pareto前沿面：所有非支配解组成的平面称为Pareto前沿面（Non-dominated front）。在目标函数较多时，前沿面通常为超曲面。

（4）非支配排序：非支配排序的过程是将解集中的所有解按照其非支配级别进行排序。首先，找出所有非支配解，这些解构成第一非支配前沿（Front 1）。然后，从剩余解中继续找出非支配解，构成第二非支配前沿（Front 2），以此类推，直到所有解都被分配到某个非支配前沿为止。

二、相关数学公式

1.支配关系的数学公式

虽然支配关系没有直接的数学公式来表示（因为它涉及到多个目标函数的比较），但可以通过以下逻辑条件来表达：

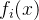
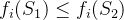
（1）对于所有目标函数 $f_{i}(x)$ ，都有 $f_{i}(S_{1})\leq f_{i}(S_{2})$ （ $S_{1}$ 不差于 $S_{2}$ ）。

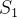
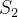
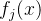
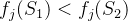
（2）存在至少一个目标函数 $f_{j}(x)$ ，使得 $f_{j}(S_{1})< f_{j}(S_{2})$ （ $S_{1}$ 在至少一个目标上严格优于 $S_{2}$ ）。

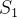
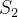
2.拥挤距离公式

在非支配排序中，拥挤距离是一种用于保持种群多样性的机制。它衡量了某个解在目标函数空间中的“拥挤”程度，即该解周围其他解的密集程度。拥挤距离的计算公式通常与目标函数的个数和每个目标函数上的距离有关。

对于一个解d在当前种群D上的拥挤距离(d,D)，其计算公式可能涉及多个目标函数上的距离计算，以及当前种群中每个目标函数的最大值和最小值。

三、非支配排序的过程

非支配排序的过程实际上是对解空间中的解进行分层的过程，具体步骤如下：

（1）初始化：

设所有解的集合为S，从中找出非支配解集合，记为F1。

（2）迭代分层：

令S=S-F1，即从S中移除已找到的非支配解集F1。

从更新后的S中再找出非支配解集合，记为F2。

重复上述步骤，直到S为空集。

（3）排序：

将每次找出的非支配解进行排序，得到{F1, F2, …, Fn}。其中，F1中的解是最优的，F2中的解次之，以此类推。

图2 非支配排序的过程

四、非支配排序的特点与应用

1.特点：

（1）非支配排序能够有效地区分不同解之间的优劣关系。

（2）通过分层的方式，可以清晰地展示出解空间中的Pareto前沿面。

2.应用：

（1）非支配排序广泛应用于多目标优化算法中，如NSGA-II（带精英策略的非支配排序遗传算法）等。

（2）在这些算法中，非支配排序用于对种群中的个体进行排序和选择，以指导算法的进化方向。

五、非支配排序与多目标优化的关系

多目标优化问题通常涉及多个相互冲突的目标，需要找到一组折衷的解（即Pareto最优解集）。非支配排序正是用于解决这一问题的一种有效方法。通过非支配排序，可以将解空间中的解按照优劣关系进行分层和排序，从而帮助决策者从Pareto最优解集中选择一个合适的解作为最终解决方案。

注意事项：

（1）多目标优化的复杂性：多目标优化问题通常涉及多个相互冲突的目标函数，因此很难找到单个解使得所有目标函数都达到最优。非支配排序正是为了解决这一问题而提出的。

（2）算法实现：在实际算法实现中，非支配排序通常与遗传算法等优化算法相结合，以迭代的方式搜索最优解集。

六、非支配排序的完整示例

假设我们有两个目标函数 f1(x) 和 f2(x)，需要对种群进行非支配排序。以下是一个具体的实现过程（python代码）：

1. 初始化种群

假设种群大小为5，每个个体的决策变量为一个实数，随机生成初始种群：

import random

# 初始化种群

population = [random.uniform(-55, 55) for _ in range(5)]

2. 定义目标函数

定义两个目标函数：

# 目标函数1def function1(x):

return -x**2

# 目标函数2def function2(x):

return -(x - 2)**2

3. 非支配排序算法

实现快速非支配排序算法：

def fast_non_dominated_sort(values1