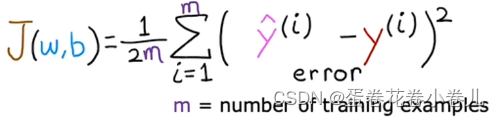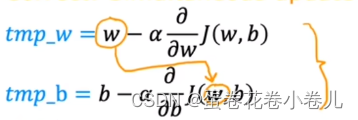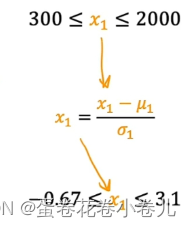线性回归

代价函数

最常用的均方误差：

y^hat: x预测出来的y值
y:原训练样本中的y值，也就是标准答案

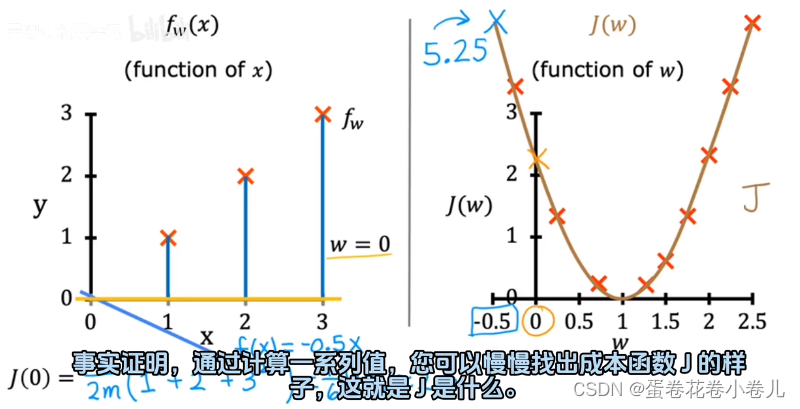
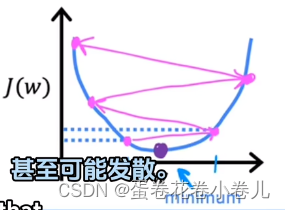
用上面的公式可以算出w不同时，J的数是多少，最后做出下图：

J衡量平方误差有多少，所以要最小化w对应的值，使得模型最好。

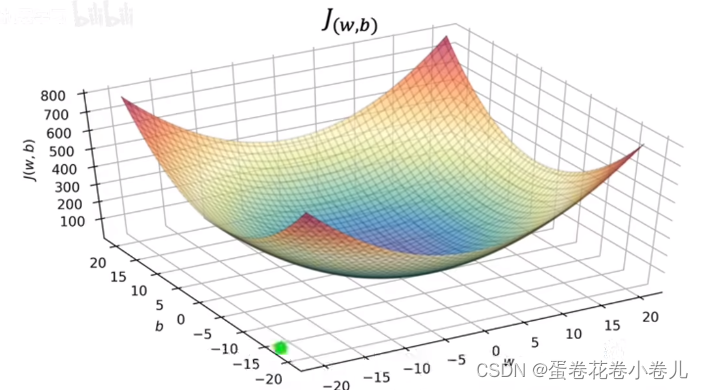
其可视化可以用3D或者等高线来表示：

梯度下降法

w = tmp_w
b = tmp_b

学习率：α（太小，下降太慢；太大，一部就下去了，甚至超过了最小值）

多元线性回归

多元线性回归的每一个特征X都有对应的W，多元是指具有多个X

向量化

可以让代码简短，运行时间减少

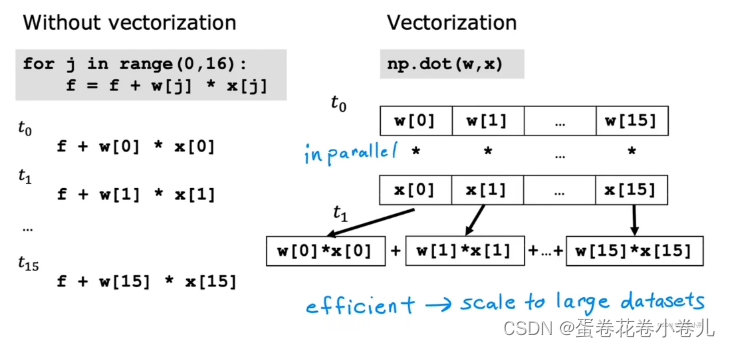
• 左边的for循环代码是不使用向量化的，计算机只会一步一步的执行，即在每一个时间戳上只会计算一次
• 右边的向量化代码，计算机第一步就会同时并行的将每对w和x相乘，第二步会获取这16个数据，并用专门的硬件非常高效的求和，并不需要一步一步把这16个数据加起来
  （参考：https://blog.csdn.net/u011453680/article/details/130222991）

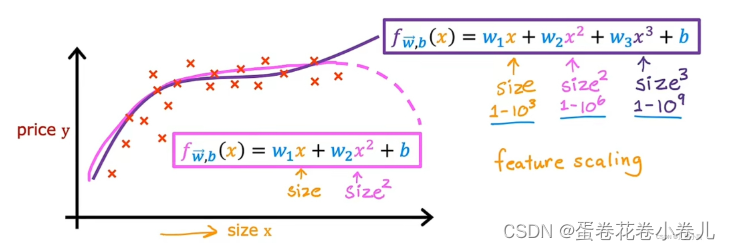
特征缩放

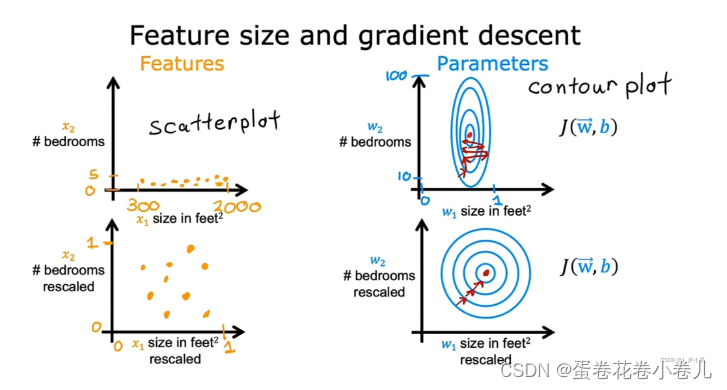
两个特征的可能值范围差距过大时，所对应的参数的可能值范围差距也会过大，产生的成本函数的等高线图为椭圆形，会让梯度下降算法在运行时来回横跳很长一段时间，才能找到J函数的全局最小值。进行特征缩放，转换后的数据重新画成本函数J的等高线图，J函数为圆形，此时采用梯度下降算法，可以找到一条更直接的通往全局最小值的路，不会再左右横跳浪费时间了。

常见的特征缩放方法

1. 除以最大值法
将特征的可能值均除以可能值范围的最大值

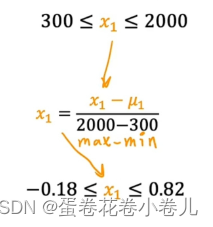
2. 均值归一化
使特征的可能值会围绕零点，既有负值又有正值

值 = 值 - 平均值 / 范围的max - min

3. Z-score 标准化
https://blog.csdn.net/YHKKun/article/details/136620077?utm_source=miniapp_weixin
值 = 值 - 平均值 / 标准差

是否需要特征缩放

不能太大或者太小，否则需要特征缩放。

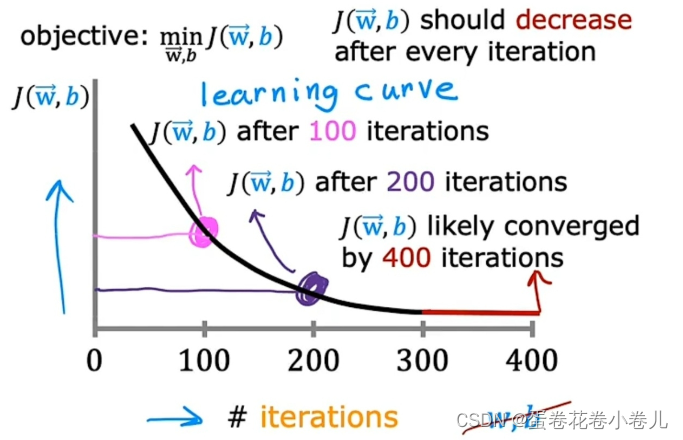
梯度下降是否收敛：画学习曲线

学习曲线平坦时，梯度下降算法收敛。

x轴是梯度下降算法的迭代次数，y轴是成本函数J的值。

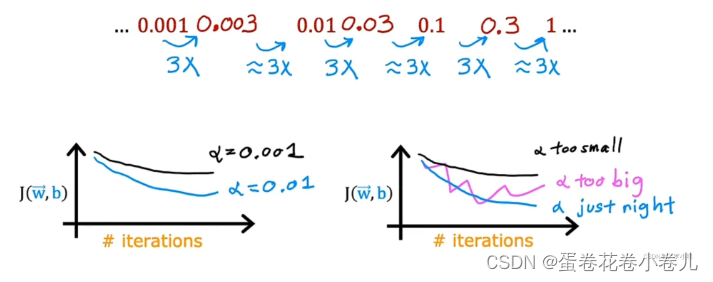
学习率如何设置

1. 选择 α 学习率的方法：
   

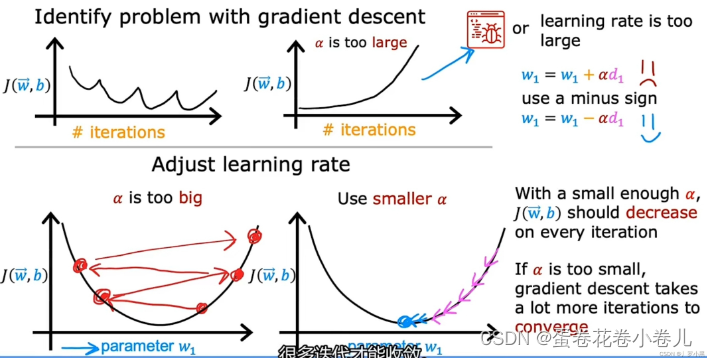
2. 出现波浪型或向上递增型，表示梯度下降算法出错
   学习率α过大，或代码有bug导致
   

3. 这个时候我们需要对学习率进行调整。
   学习率调整方法：
   基本主要思想都是：随着迭代，学习率进行一次次的减小
   https://www.cnblogs.com/lliuye/p/9471231.html

多项式回归