上节了解了卷积层的原理，本节以图像为例，介绍一下它的实际应用

1 互相关运算

严格来说，卷积层是个错误的叫法，因为它所表达的运算其实是互相关运算（cross-correlation）。

首先，我们暂时忽略通道（第三维）这一情况，看看如何处理二维图像数据和隐藏表示。输入的二维张量形状是$3\times 3$，卷积核的形状是$2\times 2$，计算如下图：
在二维互相关运算中，卷积窗口从输入张量的左上角开始，从左到右、从上到下滑动。 当卷积窗口滑动到新一个位置时，包含在该窗口中的部分张量与卷积核张量进行按元素相乘，计算步骤如下：$$\begin{array}{r}0\times 0+1\times 1+3\times 2+4\times 3=19,\\ 1\times 0+2\times 1+4\times 2+5\times 3=25,\\ 3\times 0+4\times 1+6\times 2+7\times 3=37,\\ 4\times 0+5\times 1+7\times 2+8\times 3=43.\end{array}$$

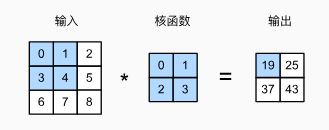
输出大小等于输入大小$n_h\times n_w$减去卷积核大小$k_h\times k_w$，即：$$(n_h-k_h+1)\times (n_w-k_w+1).$$
下面是手动实现一个二维互相关运算：

import torch

# x是输入张量，k是卷积核张量
def corr2d(x,k):
    # 确定输出张量的大小
    y=torch.zeros(x.shape[0]-k.shape[0]+1,x.shape[1]-k.shape[1]+1)
    for i in range(y.shape[0]):
        for j in range(y.shape[1]):
            y[i,j]=(x[i:i+k.shape[0],j:j+k.shape[1]]*k).sum()
    #X[i:i + h, j:j + w] 提取输入矩阵 X 中从位置 (i, j) 开始，大小与卷积核 K 相同的子区域。
    return y

X = torch.tensor([[0.0, 1.0, 2.0], [3.0, 4.0, 5.0], [6.0, 7.0, 8.0]])
K = torch.tensor([[0.0, 1.0], [2.0, 3.0]])
corr2d(X, K)

运行结果：

2 卷积层

卷积层对输入和卷积核权重进行互相关运算，并在添加标量偏置之后产生输出。 所以，卷积层中的两个被训练的参数是卷积核权重和标量偏置。

下面将基于上面定义的corr2d函数实现二维卷积层。在__init__构造函数中，将weight和bias声明为两个模型参数。前向传播函数调用corr2d函数并添加偏置。

class Conv2d(nn.Module):
    def __init__(self,kernel_size):
        super().__init__()
        self.weight=nn.Parameter(torch.rand(kernel_size))
        self.bias=nn.Parameter(torch.zeros(1))

    def forward(self,x):
        return corr2d(x,self.weight)+self.bias
        # 对输入和卷积核权重进行互相关运算，并在添加标量偏置之后产生输出

3 图像中目标的边缘检测

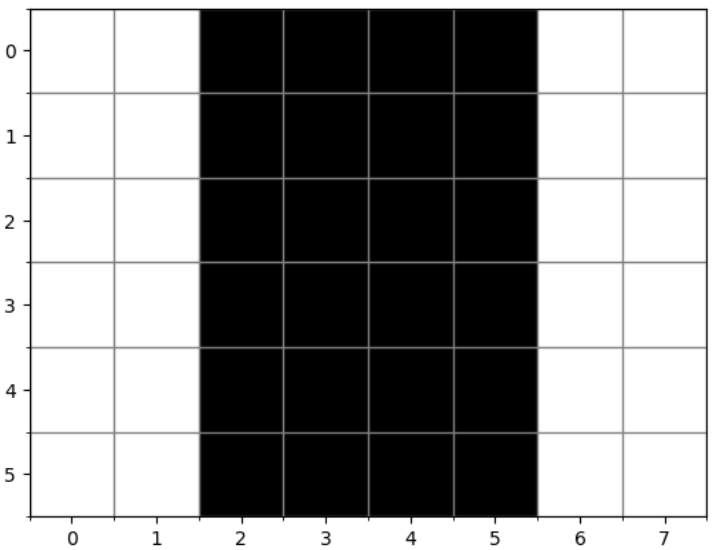
如下是卷积层的一个简单应用：通过找到像素变化的位置，来检测图像中不同颜色的边缘。 首先，我们构造一个$6\times 8$像素的黑白图像:

import matplotlib.pyplot as plt
X = torch.ones((6, 8))
X[:, 2:6] = 0
print(X)

可视化一下是下面这样：

接下来我们构造一个$1\times 2$的卷积核$k$，数值为$[1.0,-1.0]$，观察矩阵可知，当进行互相关运算时：

1. 如果水平相邻的元素相同，则输出为零
2. 如果水平相邻的元素不同，则输出为非零

现在进行运算：

K = torch.tensor([[1.0, -1.0]])
Y = corr2d(X, K)
Y

运行结果：

结果分析： 输出Y中的1代表从白色到黑色的边缘，-1代表从黑色到白色的边缘，其他情况的输出为0

但是如果我们把输入的二维图像转置，再进行互相关运算，输出如下：

corr2d(X.t(), K)

运行结果：

说明该卷积核只能检测垂直边缘，无法检测水平边缘

4 卷积核

上述检测黑白边缘的例子中，我么使用的是$[1,-1]$的卷积核，但是面对更加复杂，或者连续的卷积层时，手动设计卷积核不现实，所以我们希望通过计算梯度来自动更新卷积核。

下面我们将使用内置的卷积层，并暂时忽略偏置，这里补充一点nn.Conv2d的输入格式和输出格式都是$（批量大小、通道、高度、宽度）$：

# 构造一个二维卷积层，它具有1个输出通道和形状为（1，2）的卷积核
conv2d = nn.Conv2d(1,1, kernel_size=(1, 2), bias=False)

# 其中批量大小和通道数都为1
X = X.reshape((1, 1, 6, 8))
Y = Y.reshape((1, 1, 6, 7))
lr = 0.001  # 学习率

for i in range(400):
    Y_hat = conv2d(X)
    l = (Y_hat - Y) ** 2
    conv2d.zero_grad()
    l.sum().backward()
    # 迭代卷积核
    conv2d.weight.data[:] -= lr * conv2d.weight.grad
    if (i + 1) % 100 == 0:
        print(f'epoch {i+1}, loss {l.sum():.3f}')

conv2d.weight.data.reshape((1, 2))# 输出卷积核的权重张量

运行结果：

可以看到400次迭代后，误差已经足够低了，而且卷积核的权重是$[0.9910,-0.9910]$，已经非常接近我们之前定义的卷积核的权重了

5 特征映射和感受野

①特征映射：输出的卷积层有时被称为特征映射（feature map），因为它可以被视为一个输入映射到下一层的空间维度的转换器。

②感受野：在卷积神经网络中，对于某一层的任意元素$x$，其感受野是指在前向传播期间可能影响$x$计算的所有元素（来自所有先前层）。