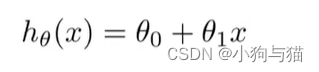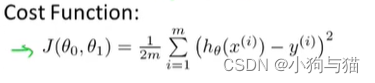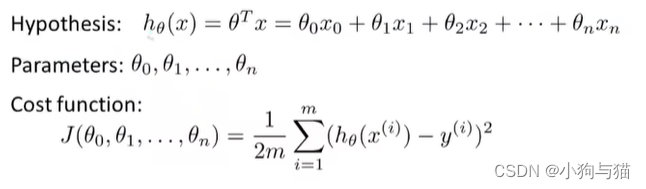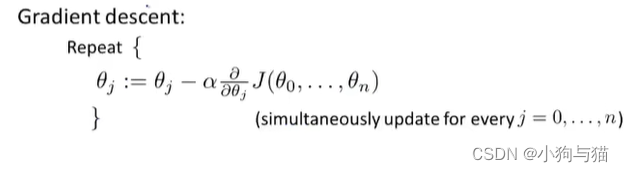一 绪论
1.监督学习
给定一个数据集,且已经表明了“正确答案”
1.1回归问题:预测一个连续值输出;分类问题:预测一个离散值输出
2.无监督学习
给定一个未表明意义的数据集,将其分簇(聚类算法)
3.代价函数:平方误差函数
4.梯度下降算法:
从某个固定的参数值开始,逐渐改变参数值,寻找最小的代价函数值或局部最小
4.1同步更新:
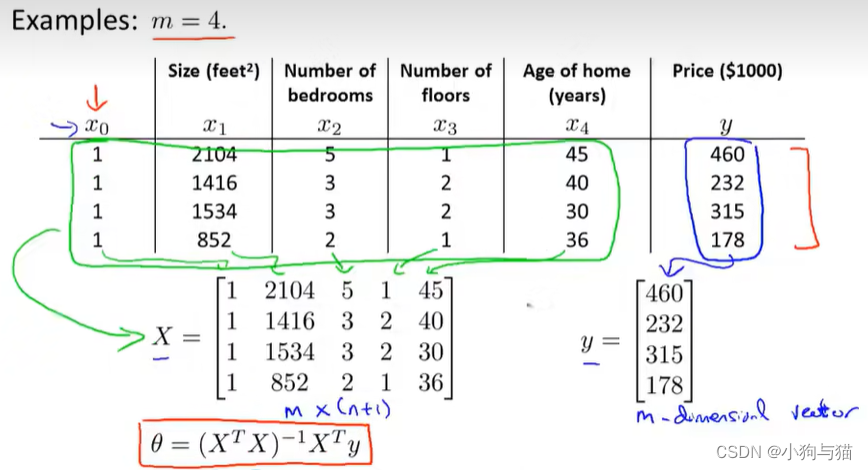
4.2 多元线性回归:
4.3特征缩放
将特征向量的取值范围进行调整,至所有的取值范围在同一个范围内
将取值范围再调整,至取值范围包含0
4.4学习率的取法:
5.正规方程
用于求最小的代价所对应的sitar值
当出现X的转置和X的乘积不可逆的情况时,要查看是否设置了多余的特征向量
梯度下降算法和正规方程的比较:
二.octave常用命令
1.基本操作命令:
%:注释
~=:不等于
xor:异或
PS1:('>> '); :隐藏命令提示信息
disp(输出字符串的代码):打印字符串
format 变量类型:设置输出的默认数据类型
pwd:显示当前路径
2.矩阵构造命令:
[0:0.01:0.98]:从0到0.98间隔为0.01的数列
eye(n):生成n阶单位矩阵
size(矩阵):返回矩阵的行和列
length(矩阵):返回矩阵的最大维度
ones/twos (行,列):输出指定行列的全为1或2的矩阵
rand(行,列):输出指定行列的随机值矩阵
hist(矩阵):绘直方图
who:显示所有的变量
whos:显示更详细的所有变量信息
clear 变量名:删除变量
新变量名=旧变量名(1,n):将旧变量第一列的前n个数据赋值给新变量
save 文件名 变量名 (可加上-ascii):保存变量名至文件中
load 文件名:若文件中无变量,只有数据,则将文件名作为一个变量处理,文件中的数据作为一个矩阵,若有变量,则会读入变量
矩阵名(m,n):访问矩阵指定的索引的元素
矩阵名(m,:):访问矩阵第m行的所有元素
矩阵名([m,n],;):访问第m,n行的所有列元素
矩阵A=(A,含有一列元素的列向量):相当于给A加一列元素
3.矩阵运算命令:
A*B:矩阵乘法运算
A.*B:矩阵对应的元素相乘(.代表元素的运算)
A.^2:将矩阵A的各个元素平方
1./A:A的各个元素求倒数
log(A):将各个元素作为对数
exp(A):将各个元素作为指数
abs(A):各个元素求绝对值
A+x:各个元素加x
A‘ :A的转置
flipud(A):A垂直翻转
max(A):每一列的最大值
[val,ind]=max(A):val对应每一列的最大值,ind对应最大值的行坐标
A<x:生成一个各个元素与x比较的结果生成的矩阵
find(A<x):返回小于x的所有元素
[r,c]=find(A<x):r和c分别对应A中小于x的元素的行和列坐标
magic(n):生成一个行,列,对角线值的和都相等的n阶矩阵
sum(A):各个元素求和
prod(A):各个元素的乘积
floor(A):各个元素向下取整
ceil(A):各个元素向上取整
pinv(A):求逆矩阵
max(A,[],1):求每一列(第一维度)的最大值
max(A,[],2):求每一行(第二维度)的最大值
sum(A,1):求每一列的最大值
sum(A,2):求每一行的最大值
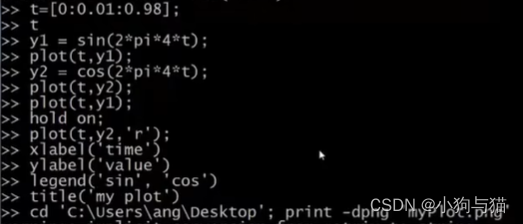
3.图像绘制命令:
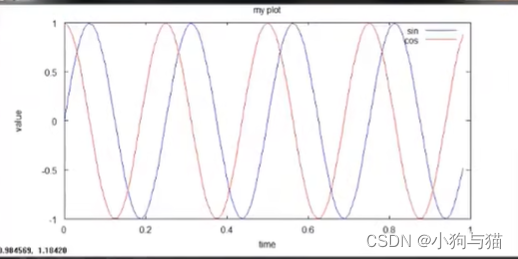
plot(横坐标取值范围,基于横坐标的函数,颜色代号):生成一个图像
hold on:保持当前图像状态,再输入一个图像时可同时显示两个图像
xlabel:设置横坐标标签
ylabel:设置列坐标标签
legend(’曲线名1‘,’曲线名2‘):设置各个曲线的名称
title:整个图像命名
print -dpng 图像名:保存图像
close:关闭图像

figure(图像代号);plot命令:分别绘制各个代号的图像
subplot(m,n,i):生成m行n列个网格,目前要使用第i个(一个网格可以绘制一个图像)
axis(r1,r2,c1,c2):修改行坐标和列坐标的范围为[r1,r2]和[c1,c2]
clf:清除图像
imagesc(A):各个元素的值对应颜色分类的范围值
4.控制命令
5.函数定义与调用
1.在某个文件中定义某个函数,在文件所在路径下调用函数
2.计算代价函数:costFunctionJ(X(自变量),y(因变量),预测函数)
三.分类
1.决策界限:
逻辑回归简化代价函数:
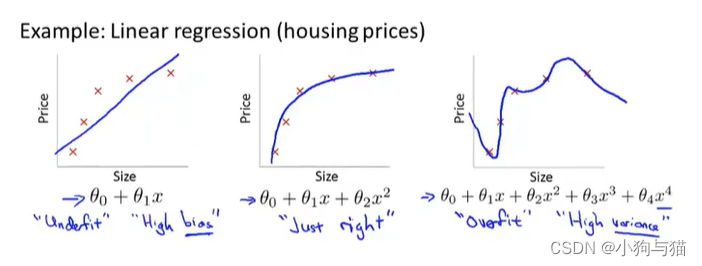
四.过度拟合
1.概述
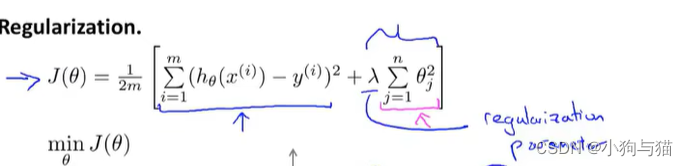
2.正则化
五.神经网络
1.概述与举例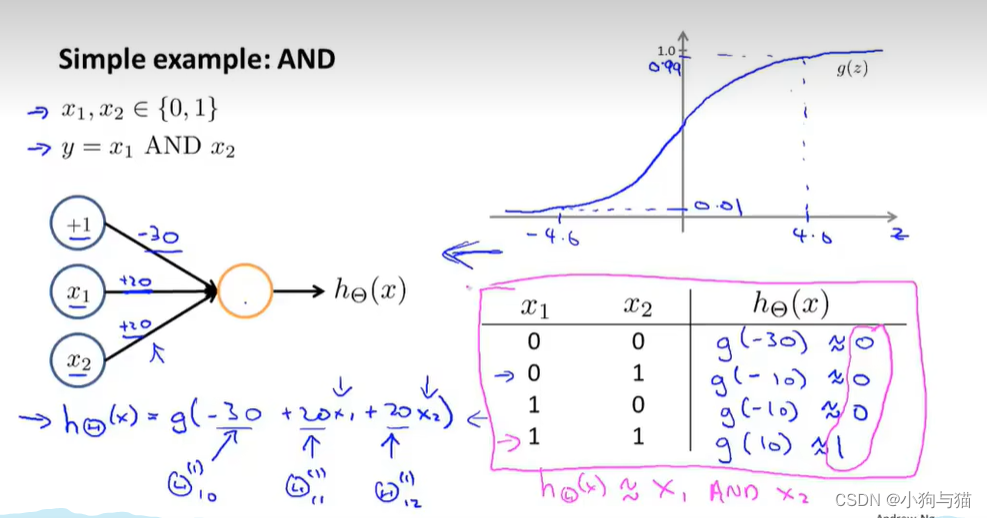

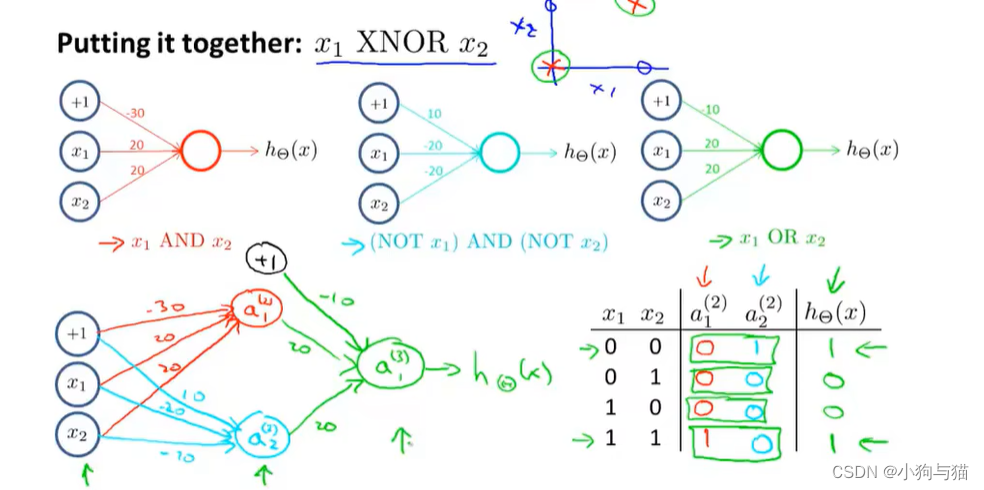
2.神经网络的代价函数:
3.反向传播算法
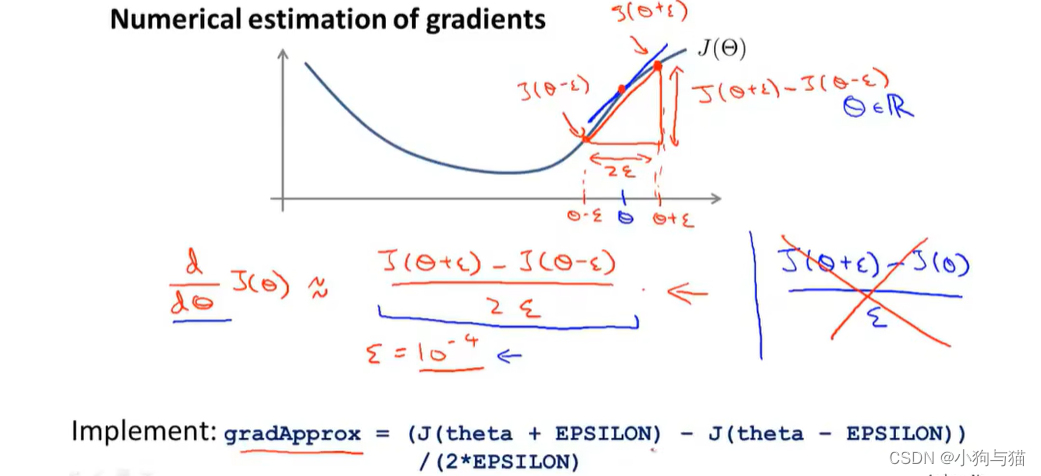
4.求某一点的近似导数
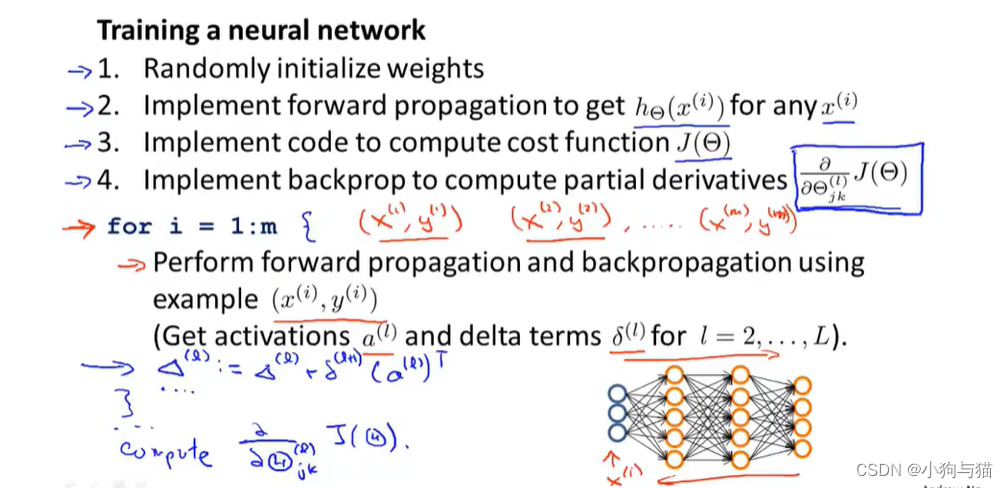
5.总体流程
 六.假设
六.假设
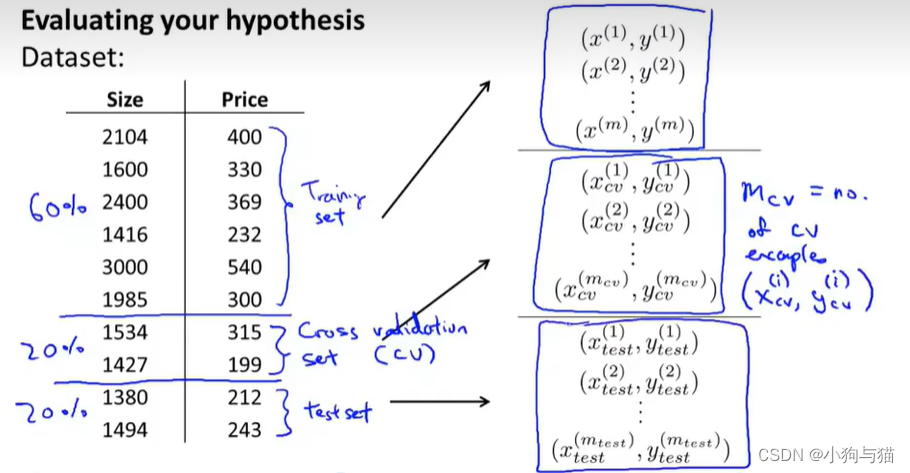
1.评价假设
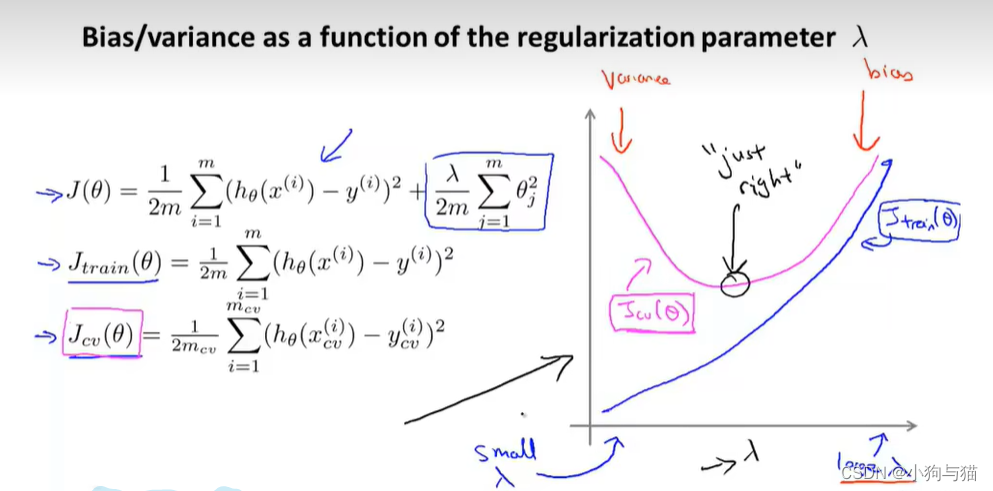
2.诊断偏差和方差
3.正则化参数与方差和偏差
七.算法设计
1.误差分析
可以先设计一个简单的算法,通过手动验证,查看哪些部分表现不好,哪些部分需要设计更加复杂的算法,哪些部分是可以忽略的
要尝试新的想法和算法,手动验证其好坏,注意验证时要使用交叉验证集
2.数据数量
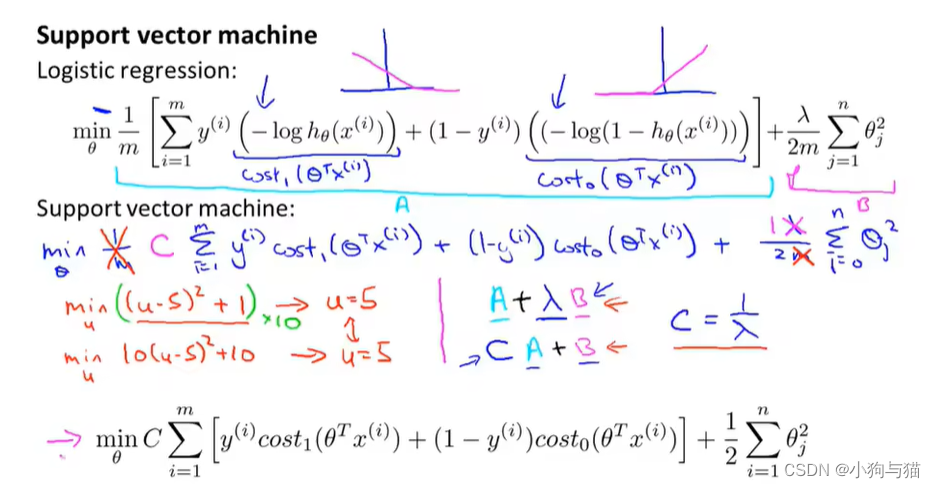
八.向量机
1.目标
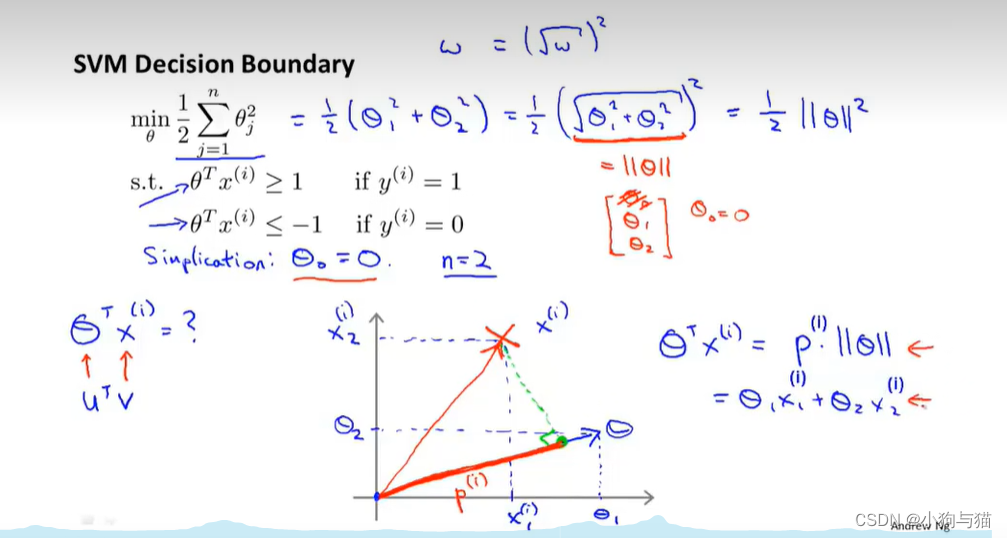
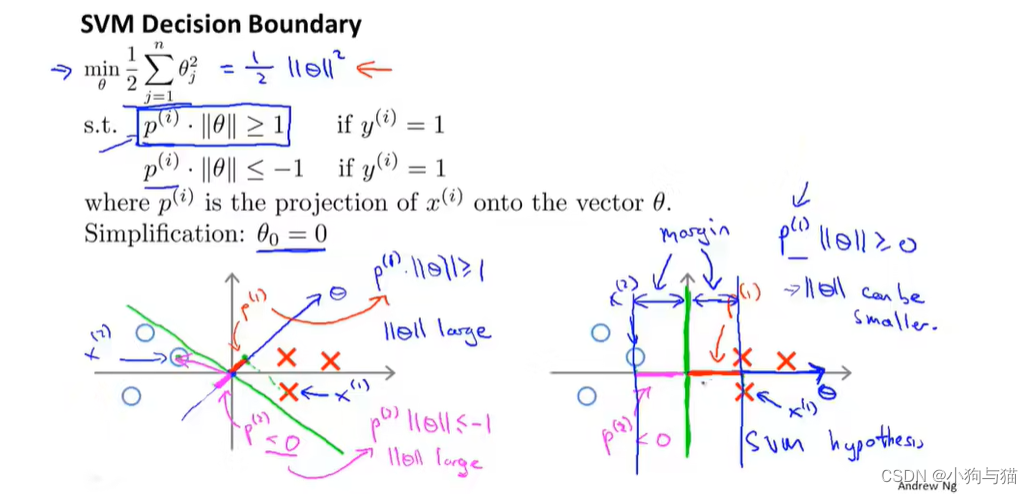
2.最大间距 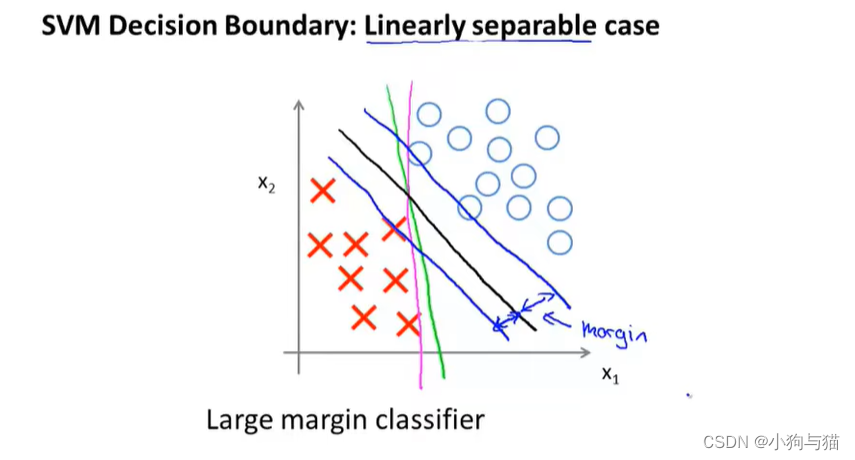
3.数学原理
尽量使theta更小
4.核函数
参数:
逻辑回归;线性核函数;高斯核函数的选择场景:
九.无监督算法
1.K均值算法
1.1算法概述
1.2.优化目标
1.3聚类中心初始化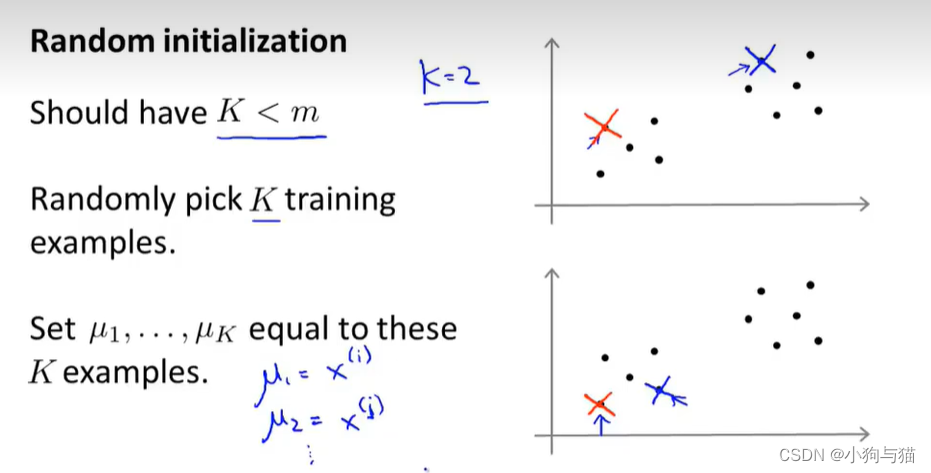
多次随机初始化,选择最小的畸变函数值
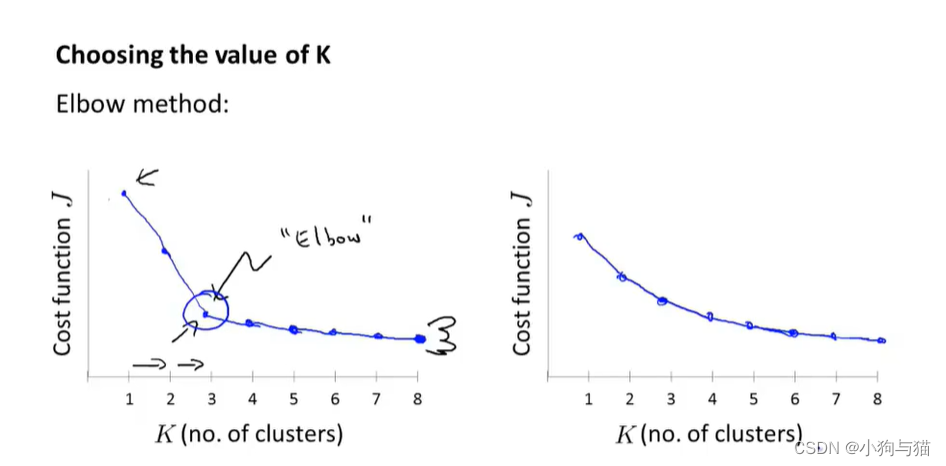
1.4聚类数量的选择
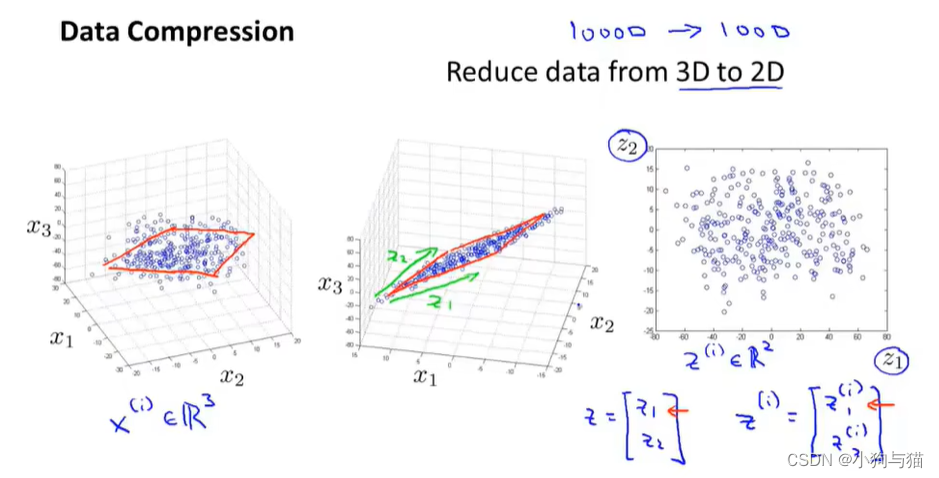
2.降维
压缩重现: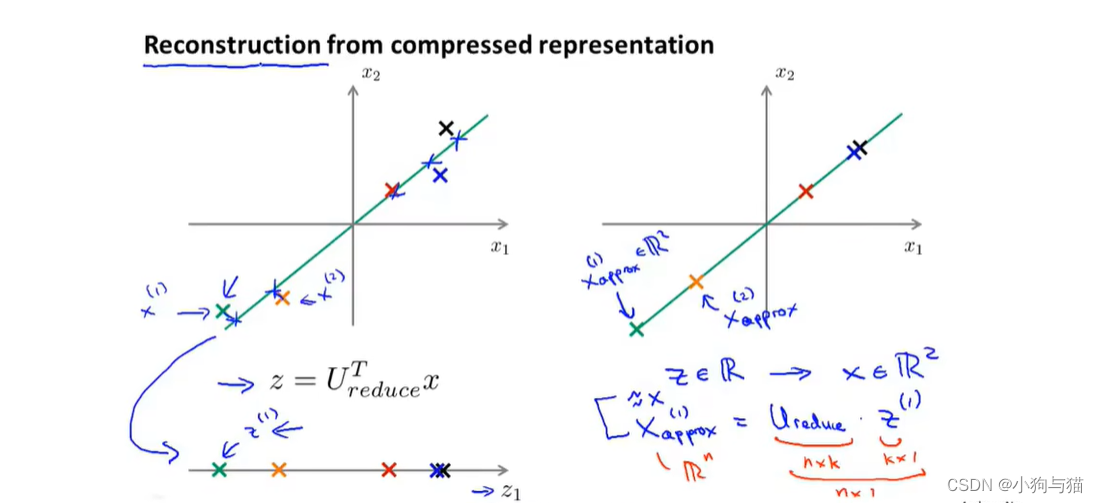
3.PCA
3.1主成分数量选择:
3.2 PCA应用:
3.3.PCA误用
可以用PCA加速算法,但不建议防止过拟合化
4.异常检测
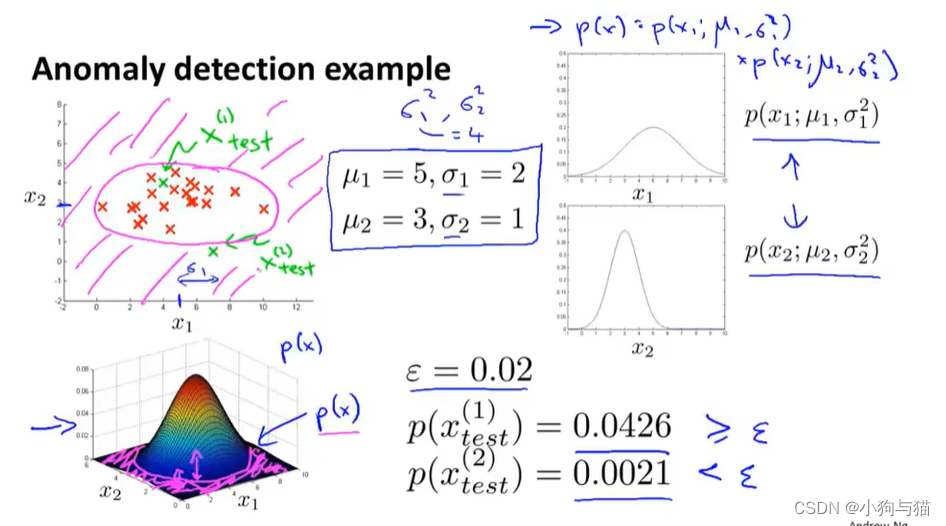
4.1异常检测算法
4.2异常检测算法应用与评估--飞机引擎
4.3异常检测算法和监督学习的比较
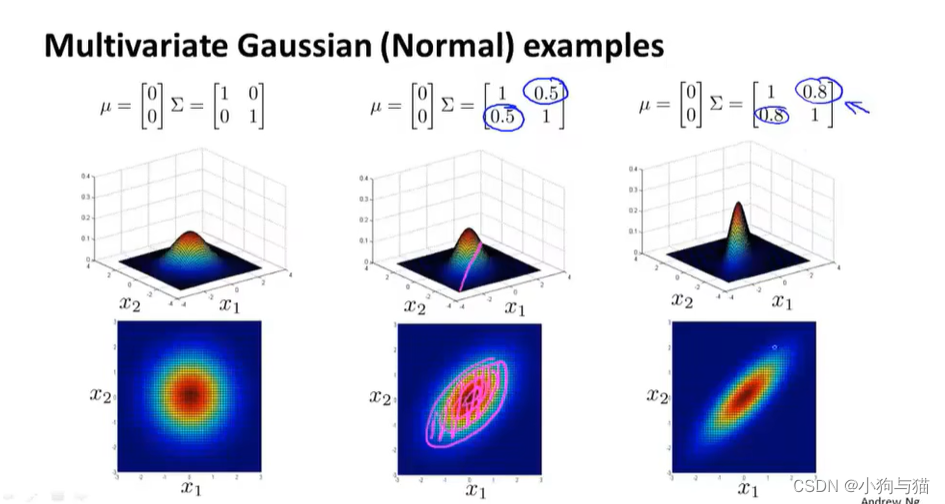
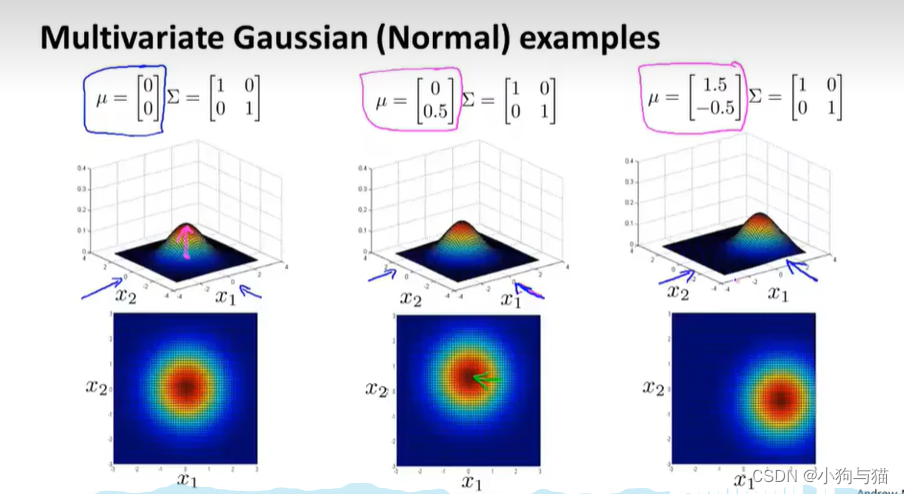
4.4多变量高斯分布
4.5多元高斯分布的异常检测 4.6多元高斯分布和原始高斯分布的比较
4.6多元高斯分布和原始高斯分布的比较
十.机器学习应用--推荐系统
1.打分系统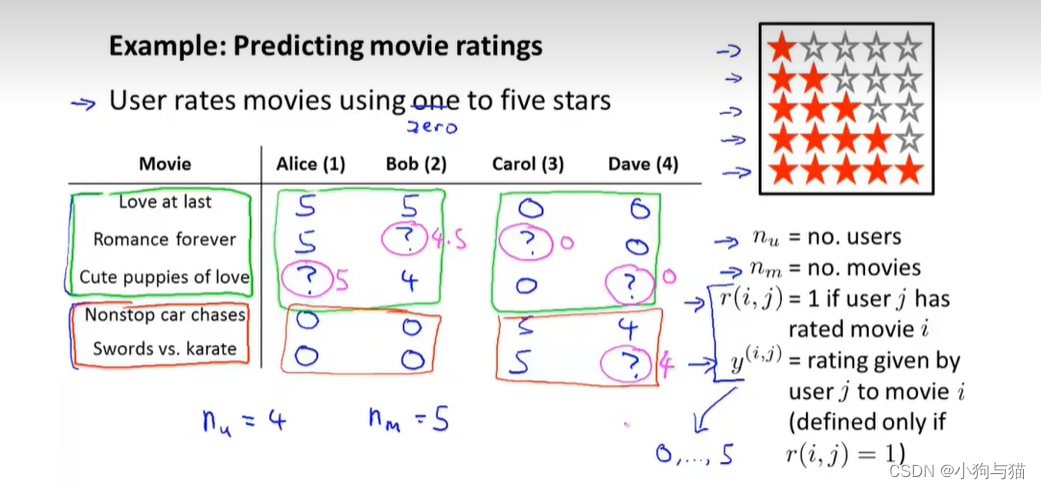
2.协同过滤算法
3.均值归一化 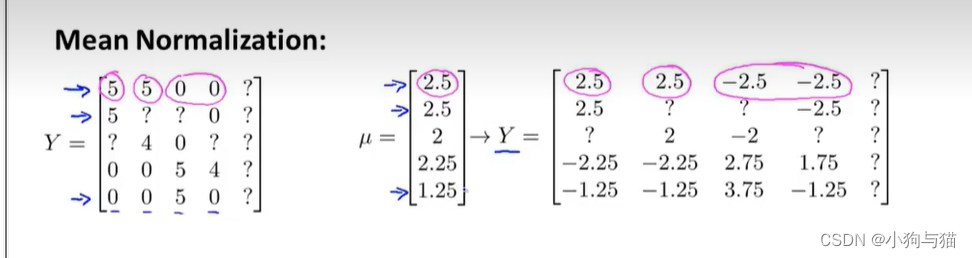
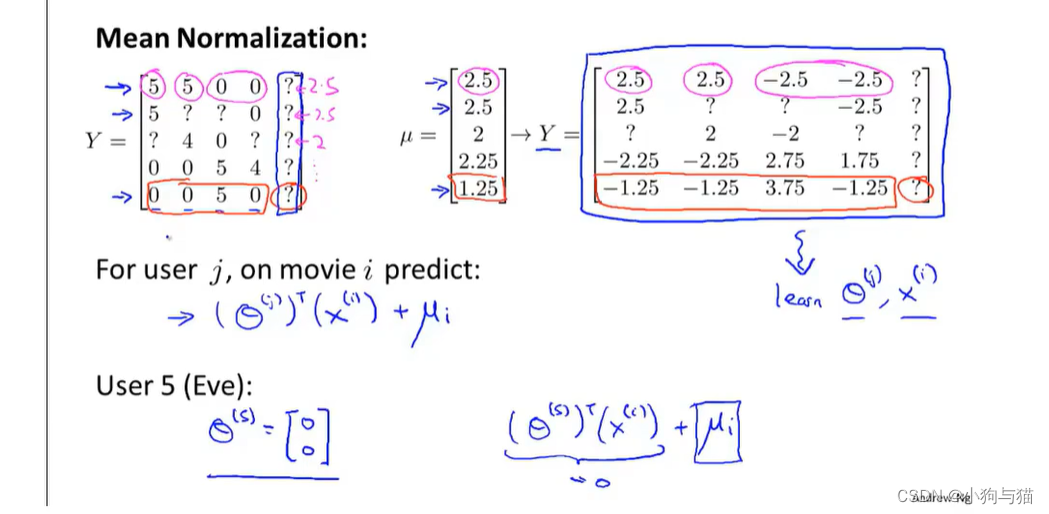
4.大数据集样本 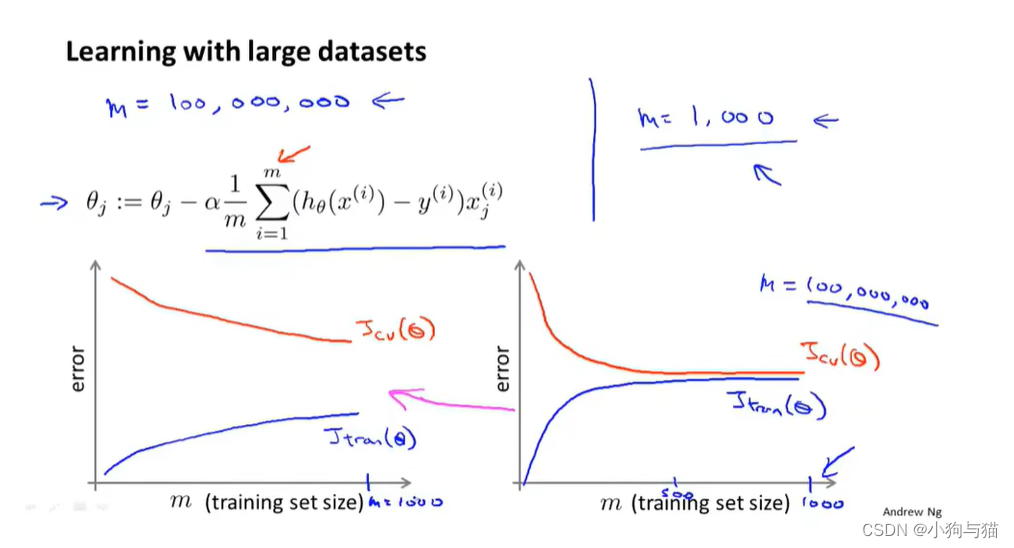
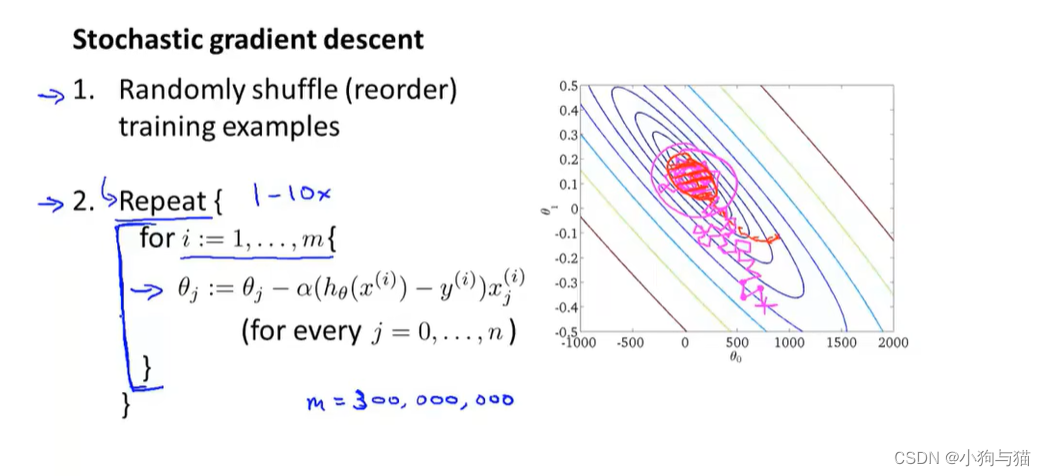
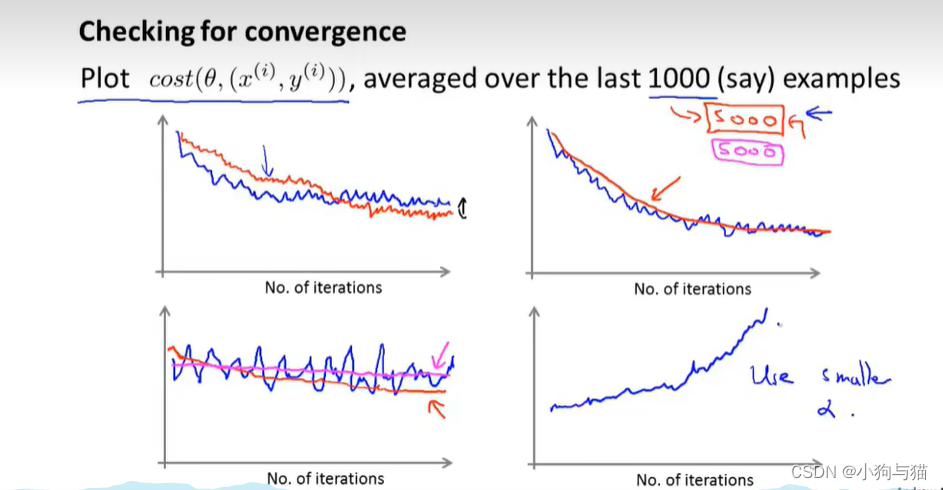
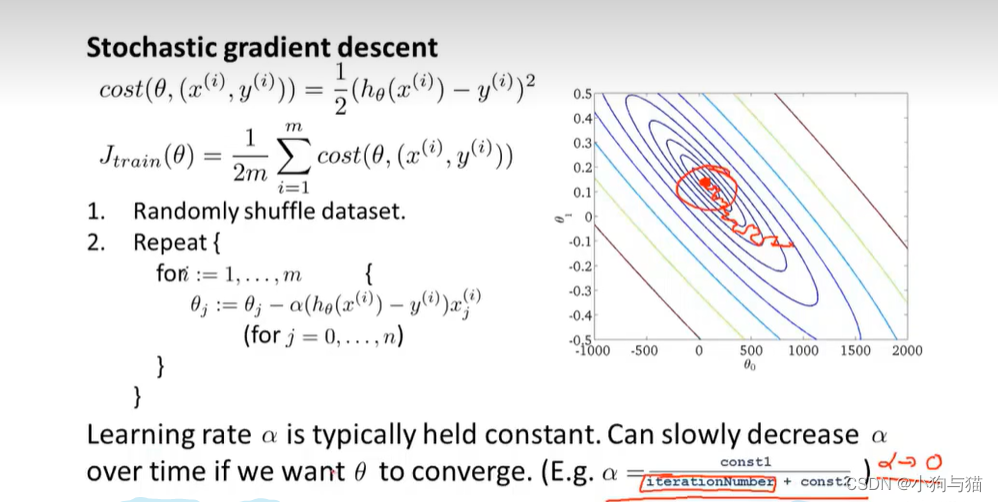
5.随机梯度算法
求代价函数时,打乱样本数据集,随机选取一个样本进行计算梯度,批量梯度算法需要将所有的样本考虑进去进行计算梯度
6.mini-batch梯度算法