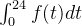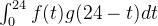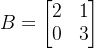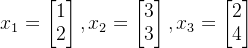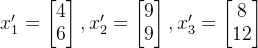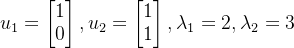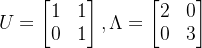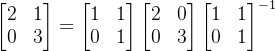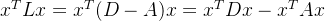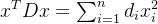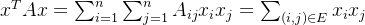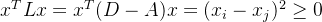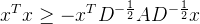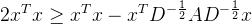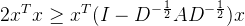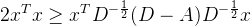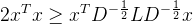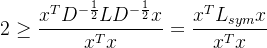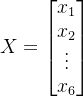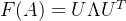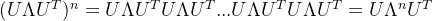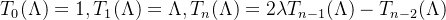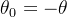这是一份用于图卷积神经网络的的入门教程,文章中包含的论证与例子不一定完全严谨,但是有助于加强对知识的理解,若有错误之处也请在评论区指出。
目录
1 预备知识
1.1 什么是卷积
学习过《信号与系统》这门课程的同学肯定对卷积的概念有深刻的印象,我在学习这门课程时经常被这个概念绕道团团转,所以卷积到底是什么,该如何通俗的理解卷积,计算机视觉领域对于图像的卷积是什么原理,这是我们需要搞明白的问题。
卷积的一般定义这样解释:
卷积(Convolution)的数学定义涉及将一个函数与另一个函数结合,从而生成一个新的函数。具体来说,卷积是一种将两个函数通过“滑动”一个函数来计算另一个函数在不同位置上的相互作用的运算。
以一维卷积入手,对于连续卷积,两个函数 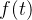
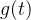
其中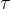
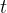
在离散的情况下,卷积定义为:
其中![f[m]](/image/aHR0cHM6Ly9sYXRleC5jc2RuLm5ldC9lcT9mJTVCbSU1RA%3D%3D)
![g[n]](/image/aHR0cHM6Ly9sYXRleC5jc2RuLm5ldC9lcT9nJTVCbiU1RA%3D%3D)

单从公式看来卷积是很抽象的,如何形象的体现卷积“卷”的过程呢?这里分别拿连续和离散的两种示例来解释卷积通过“滑动”一个函数来计算另一个函数在不同位置上的相互作用是如何操作的,关键词是“滑动”与“相互作用”。
1.1.1 离散卷积
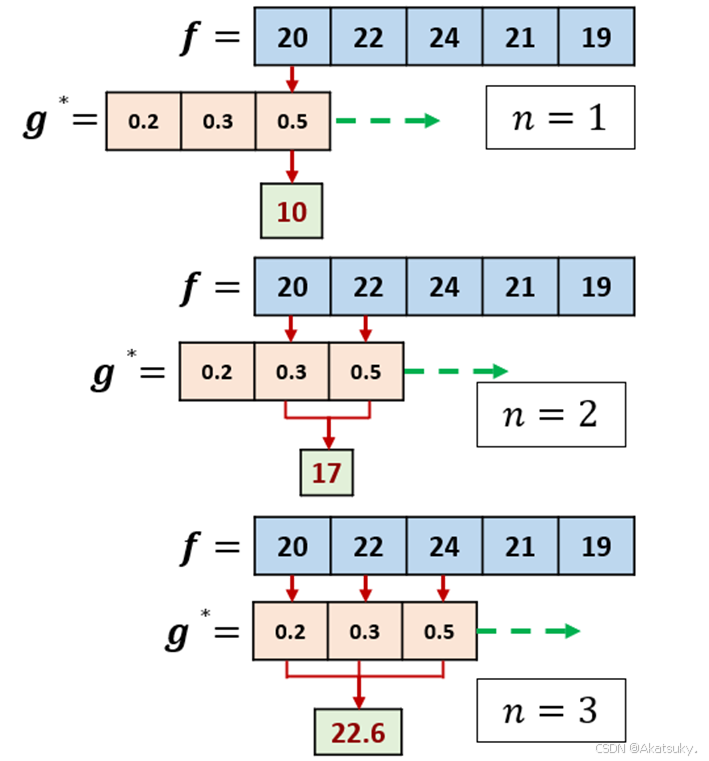
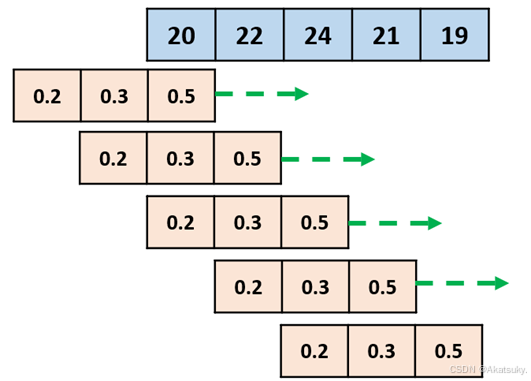
假设你正在做一个研究,探究温度是如何影响植物生长的,这里就可以引出两个离散序列:
序列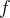
![f[m]](/image/aHR0cHM6Ly9sYXRleC5jc2RuLm5ldC9lcT9mJTVCbSU1RA%3D%3D)
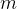
序列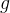
![g[1]=0.5](/image/aHR0cHM6Ly9sYXRleC5jc2RuLm5ldC9lcT9n%5B1%5D%3D0.5)
![g[2]=0.3](/image/aHR0cHM6Ly9sYXRleC5jc2RuLm5ldC9lcT9n%5B2%5D%3D0.3)
想要探究植物的生长受到过去几天温度影响的累计值,就需要用到卷积的方法,即计算一个函数在另一个函数上的作用。
离散卷积定义如下:
以上实际问题有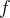
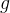


第一天的索引
以此类推,计算后四天的影响评分:
经过卷积操作后,我们得到一个新的序列,它表示植物在每一天对前几天温度的累积响应:
观察计算过程我们可以明显的发现该计算似乎是一种“加权平均”的思想,加权平均体现了序列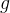
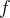
卷积的“卷”即滑动一个函数作用于另一个函数也直观地体现出来了。注意:
1.1.2 连续卷积
在日常生活和信号处理中,很多函数是连续的,这就需要用到连续卷积,公式如下:
假设你开了一家生鲜食品工厂,你的工厂的食品生产速度是时间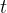
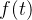
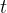
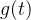
首先可以得到一天当中能够生产的生鲜产品的总量:
在一天中,第一个生产出来的产品会经历24h的腐败,一小时后生产出的产品会经历23h的腐败,以此类推。那么采用卷积的方法就可以计算24h后剩余产品的数量:
通俗的说就是最先生产出的产品最先开始腐败,这就是连续卷积的过程。
1.1.3 如何理解CNN的卷积
这里不讨论卷积神经网络的其他知识,仅仅从卷积的视角来说明在CNN(Convolutional Neural Network)中卷积是如何实现的。
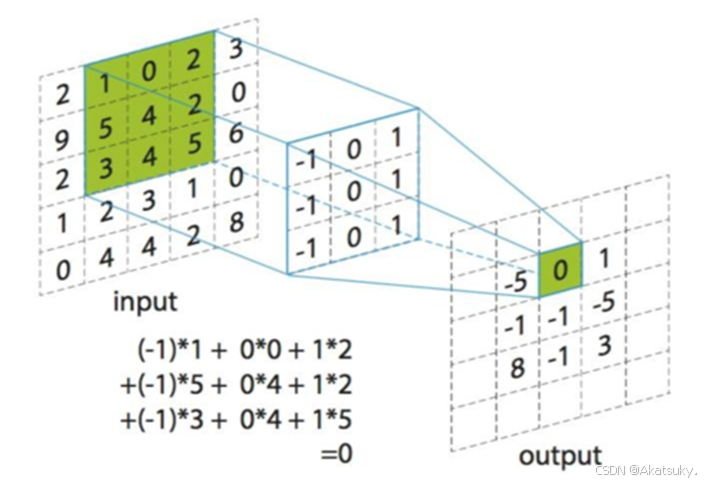
CNN的卷积于上文提到的离散卷积十分类似,CNN的作用目标大多为特定图像、视频,这类数据的特点就是有规整的拓扑结构。计算机处理图像的方式即是将图像储存为无数个像素块,每个像素块有特定的数值,以此来支持计算。
如果理解了上文提到的一维离散卷积过程,就可以很好的理解对于二维图像的卷积过程。如上图所示,input是输入的一张picture,由很多像素构成,可以对应函数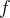
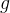
1.2 特征值与特征向量
特征值与特征向量在线性代数中的定义大致是这样的:
对于一个特定的方阵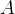
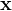
那么称
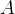
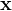
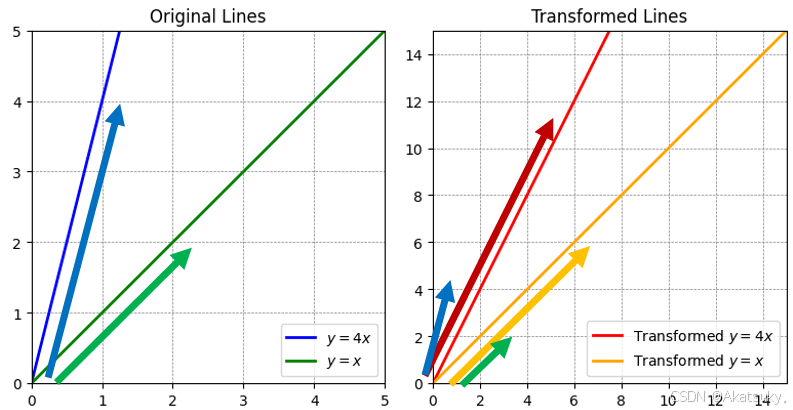
但是从定义出发还是很难理解特征值与特征向量到底是什么东西,所以用直观的例子能更好的理解其本质。首先我们知道在二维坐标系中,二维方阵其实是一种映射关系,它能够将坐标系中特定的点映射到新的位置。
我们定义一个二维方阵:
定义三个向量分别为:
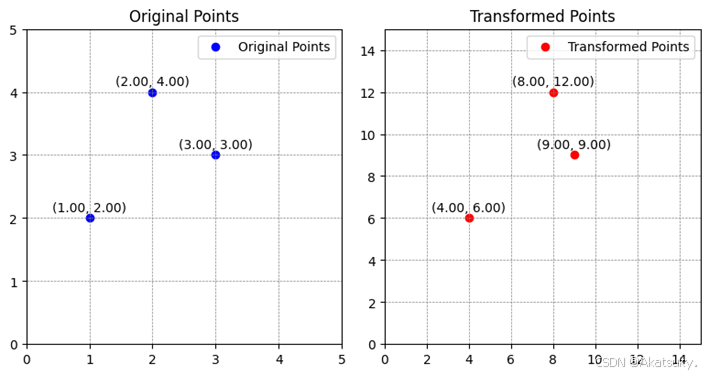
这三个向量分别经过矩阵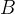
通俗的讲,方阵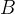
更一般的来说,在原始坐标系上取两个向量,当经过这个矩阵映射到新的空间中时,我们可以发现映射改变了向量的方向于与大小。
同样的我们重点观察绿色与黄色这个向量,此时可以发现这个向量在映射到新的空间后没有发生方向变化,仅仅大小变为原来的三倍。
以上现象说明,存在特定向量在经过映射之后不产生方向变化的向量(与自身平行),即满足以下关系:
即证明向量 ![[1,1]^T](/image/aHR0cHM6Ly9sYXRleC5jc2RuLm5ldC9lcT8lNUIxJTJDMSU1RCU1RVQ%3D)
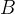

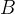
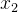

对于一个

我们再次回到本质,经过矩阵映射之后不产生方向变化的向量的特征向量,特征向量缩放的倍数为特征值。对于矩阵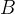
《线性代数》课程中有规范的特征向量与特征值的解,这里省略不必要的过程,得出矩阵
的两个特征向量与特征值如下:
特征向量的作用在于其方向不受映射的变化,同时两个不共线的向量可以组成该平面内任何向量,这两个性质就通俗的说明:矩阵对空间映射的变化仅与特征向量的变化有关,映射前后的变化可以用特征向量的线性组合表示。
将这两个特征向量线性组合成特征向量矩阵,将特征值化为对角矩阵我们可以得到如下结果:
由此我们的矩阵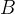
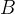
我们之前的视角是将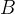
利用分解后的矩阵可以得到以下视角:
首先 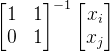
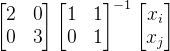
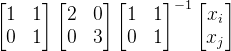
同时为了更好的理解下文内容还需要了解一些结论,这里就不一一证明:
- 如果一个矩阵是实对称阵,那么他就有
个特征值与
个互相正交的特征向量
- 一般矩阵的特征值分解为:
- 对称矩阵的特征值分解为:
- 如果一个矩阵的所有特征值大于等于零,那么就说明这个矩阵是一个半正定的矩阵
2 GCN的数学原理及推导
2.1 GCN相关概念
现在我们大致已经了解一些关于卷积的概念与线性代数的基础知识,让我们着手去研究以下图卷积网络(Graph Convolutional Network,GCN)到底是什么东西。
之前提到的离散卷积、连续卷积以及适用在CNN计算机视觉中的卷积的本质按我的理解来说就是整合邻居的信息。例如在离散卷积示例中探究温度对于植物生长的影响,采用的加权平均的思想整合了三天的温度信息为一个输出;再者,观察CNN的卷积也不难看出,卷积核整合了特定范围内的信息为一个输出。对于图结构来说,我们只需要找一个卷积核去遍历图结构整合邻居信息不就行了吗?然而事情远远没有这么简单。
回到CNN卷积的部分,我们发现CNN的作用目标大多为特定图像、视频,这类数据的特点就是有规整的拓扑结构,所以一个3*3的卷积核可以滑动遍历整个图像。但是图结构可没有这么简单。
图论中其定义如下:
- 节点/顶点 (Vertex): 图中的每个对象或元素称为节点
- 边 (Edge): 节点之间的连接关系称为边
- 邻接节点: 如果两个节点之间存在一条边,则它们被称为邻接节点。
- 无向图中的度: 一个节点的度是与它连接的边的数量。
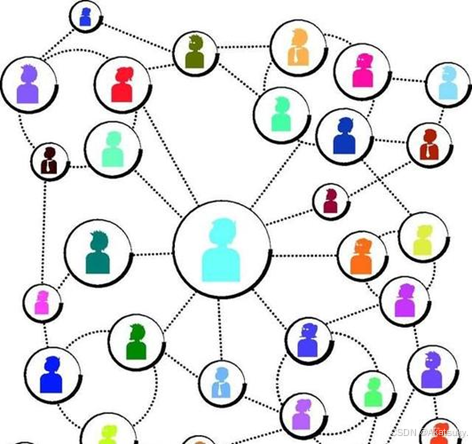
观察以上的人际关系网络图可以看出,有的节点包含8个边,有的节点只包含两个边,这就是图结构复杂拓扑结构的直观展示。所以我们无法找到一个特定形状的kernel直接在图结构的空间域上卷积。
为了实现卷积,大佬们想到的解决方案就是“傅里叶变换”,将图结构变换到另一个方便进行卷积操作域中,完成卷积后再采用逆变换将其变回空间域中。(注意这里转换操作,有没有感觉和之前特征分解采用的思想很类似)
以下我就用实际的例子来证明GCN是如何运作的:
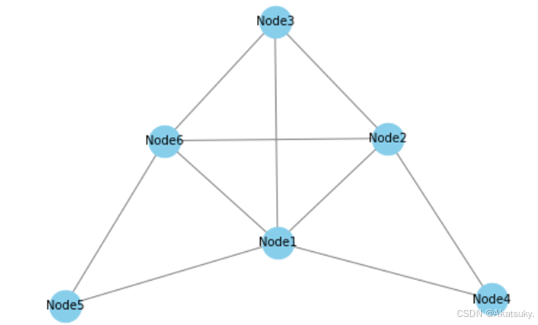
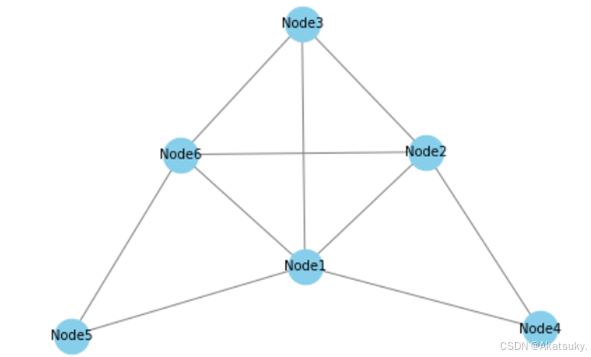
拿一个六个节点的图举例:
该图的邻接矩阵如下:
该图的度矩阵如下:
邻接矩阵和度矩阵能够很好地将图结构转化为数学语言与计算机语言,这对于计算来说是十分重要的。
2.2 拉普拉斯矩阵重要性质的证明
接下来我们引入两个概念:图的拉普拉斯矩阵(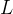

由于拉普拉斯矩阵是由图的邻接矩阵与度矩阵线性运算得到的,同时对称规范化拉普拉斯矩阵只是拉普拉斯矩阵的规范化结果,所以很容易的可以看出二者都是实对称矩阵,所以他们都有

只需要证明拉普拉斯矩阵的二次型大于等于零即能够证明拉普拉斯矩阵是半正定的:
简化后可得:
说明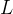

现在承接上文的结论来证明
由于:
我们定义一个新矩阵
根据Rayleigh商(Rayleigh quotient)的定义,对于任何非零向量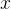
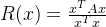


![[0,2]](/image/aHR0cHM6Ly9sYXRleC5jc2RuLm5ldC9lcT8lNUIwJTJDMiU1RA%3D%3D)
2.3 GCN卷积的实现
经过以上证明的启发,应该能看出来图的拉普拉斯矩阵对于GCN卷积来说十分重要,现在我们就来揭示图卷积神经网络的是如何整合邻居节点信息的。
还是拿这张图举例:
图中有六个节点,我们假设每个节点都包含一个常数特征,那么这个图所构成的特征向量如下所示:
同时我们已经完成了关于拉普拉斯矩阵重要性质的证明,现在我们知道拉普拉斯矩阵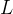
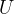
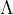
当我们采用拉普拉斯矩阵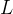
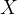
可以看出这恰恰是一种整合节点与其邻居信息的计算方法。接下来可以推导出:
其中
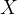
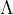
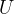
由此衍生出的一个新的问题是,该方法需要计算拉普拉斯矩阵的特征值域特征向量,但是算法复杂度为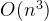
我们假设有一种函数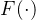
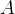
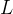
这里的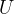
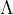
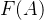
图卷积的一般过程如下:
其中



对
故可推导:
该方法是一种避免特征分解的基础解法。但是高次多项式一般会出现梯度爆炸或者梯度消失问题,所以在实际操作时采用切比雪夫多项式。
切比雪夫多项式是一种用于逼近任意函数的工具,递推公式如下:
利用这种递归形式,图卷积可以通过局部邻域的信息进行逼近,而不需要显式计算特征分解。
由于切比雪夫多项式适合在区间![[-1,1]](/image/aHR0cHM6Ly9sYXRleC5jc2RuLm5ldC9lcT8lNUItMSUyQzElNUQ%3D)
这里引入对称规范化拉普拉斯矩阵

![[0,2]](/image/aHR0cHM6Ly9sYXRleC5jc2RuLm5ldC9lcT8lNUIwJTJDMiU1RA%3D%3D)
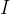
![[-1,1]](/image/aHR0cHM6Ly9sYXRleC5jc2RuLm5ldC9lcT8lNUItMSUyQzElNUQ%3D)
我们采用切比雪夫多项式逼近
其中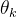
当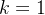
由于 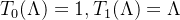
现在加入正则化:
如此便得到了与Kipf.的论文中一样的公式,在论文中作者还使用了Renormalization trick处理,处理后的结果为:
参考资料
【无痛线代】特征值究竟体现了矩阵的什么特征?_哔哩哔哩_bilibili
https://www.zhihu.com/question/22298352/answer/228543288
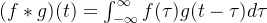
![(f*g)[n]=\sum_{m=-\infty}^{\infty}f[m]g[n-m]](/image/aHR0cHM6Ly9sYXRleC5jc2RuLm5ldC9lcT8lMjhmKmclMjklNUJuJTVEJTNEJTVDc3VtXyU3Qm0lM0QtJTVDaW5mdHklN0QlNUUlN0IlNUNpbmZ0eSU3RGYlNUJtJTVEZyU1Qm4tbSU1RA%3D%3D)
![f=[20,22,24,21,19]](/image/aHR0cHM6Ly9sYXRleC5jc2RuLm5ldC9lcT9mJTNEJTVCMjAlMkMyMiUyQzI0JTJDMjElMkMxOSU1RA%3D%3D)
![g=[0.5,0.3,0.2]](/image/aHR0cHM6Ly9sYXRleC5jc2RuLm5ldC9lcT9nJTNEJTVCMC41JTJDMC4zJTJDMC4yJTVE)
![(f*g)[1]=f[1]g[1-1]=20\times0.5=10](/image/aHR0cHM6Ly9sYXRleC5jc2RuLm5ldC9lcT8lMjhmKmclMjklNUIxJTVEJTNEZiU1QjElNURnJTVCMS0xJTVEJTNEMjAlNUN0aW1lczAuNSUzRDEw)
![(f*g)=[10,17,22.6,22.1,20.6]](/image/aHR0cHM6Ly9sYXRleC5jc2RuLm5ldC9lcT8lMjhmKmclMjklM0QlNUIxMCUyQzE3JTJDMjIuNiUyQzIyLjElMkMyMC42JTVE)
![g^*=g[n-m]](/image/aHR0cHM6Ly9sYXRleC5jc2RuLm5ldC9lcT9n%5E*%3Dg%5Bn-m%5D)