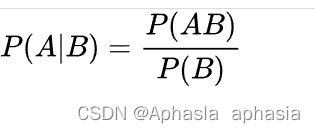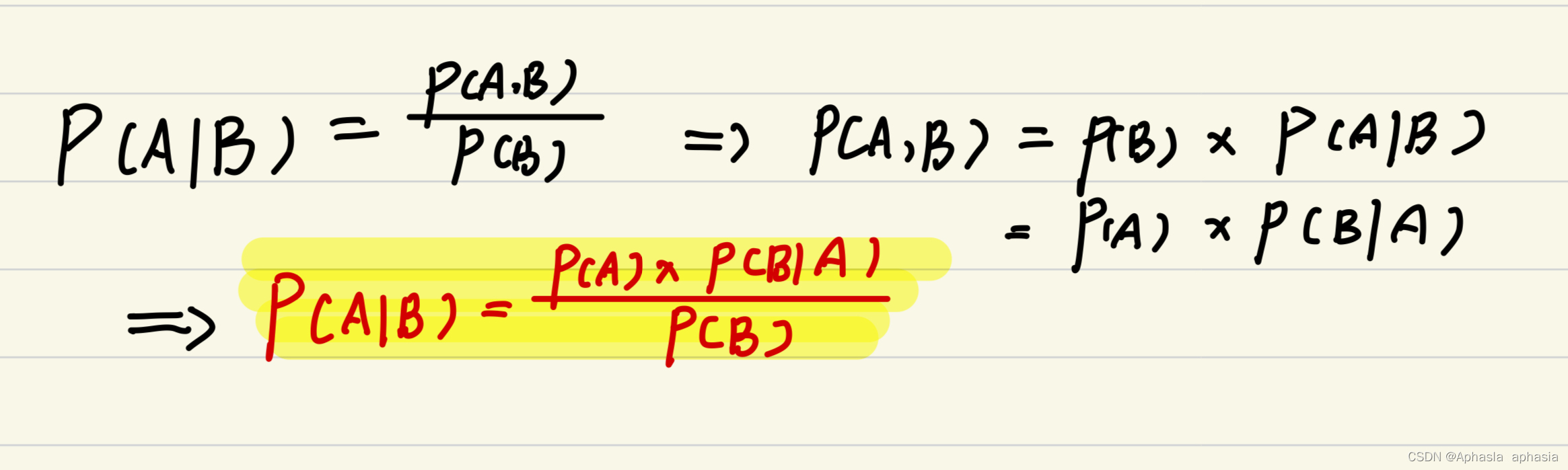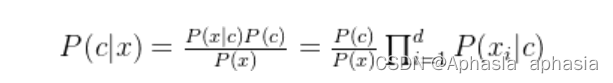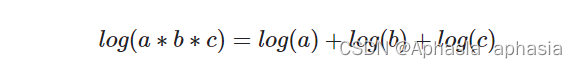一、引言

 在当今信息爆炸的时代，电子邮件成为人们日常沟通和工作中不可或缺的一部分。然而，随之而来的垃圾邮件问题也日益严重。本文将介绍如何利用朴素贝叶斯算法来识别和过滤垃圾邮箱，提高电子邮件处理效率。

二、基础知识

2.1 一些数学概率公式

（1）先验概率和后验概率：

假设我们要使用朴素贝叶斯算法来进行电子邮件的垃圾邮件分类。我们有两个类别：垃圾邮件（Spam）和非垃圾邮件（Ham）。现在我们收到了一封包含“免费优惠”这个词语的邮件，请问这封邮件属于垃圾邮件的概率是多少？

先验概率：
先验概率指的是在考虑任何证据的情况下，在我们观察到新数据之前，对事件概率的初始估计。在这个例子中，假设我们知道在所有收到的邮件中，大约有30%是垃圾邮件。那么垃圾邮件的先验概率为0.3，非垃圾邮件的先验概率为0.7。

后验概率：
后验概率是在考虑了新的数据或证据之后，根据先验概率和相应的证据来计算事件的概率。在这个例子中，我们将根据“免费优惠”这个词语在垃圾邮件和非垃圾邮件中出现的概率，来计算这封邮件属于垃圾邮件的概率，即后验概率。

综上所述，先验概率是在观察任何数据之前对事件概率的初始估计，而后验概率是在观察到新的数据或证据之后，根据先验概率和相应的证据来计算事件的概率。在朴素贝叶斯算法中，我们利用先验概率和后验概率来进行分类决策。

（2）联合概率：有多个条件同时成立的概率，记为P(A,B)

  (3)  相互独立事件：如果P(A,B)=P(A)xP(B) ，则A和B事件相互独立

（4） 指的是B事件发生的条件下，A事件发生的概率，记作P(A|B)。公式：

2.2 贝叶斯公式

贝叶斯定理是一种通过先验概率和观测数据来计算后验概率的方法，其推导过程可以通过简单的概率论知识和条件概率的定义完成。下面是贝叶斯定理的推导过程：

三、朴素贝叶斯算法

3.1 基本概念及核心思想

朴素贝叶斯算法基于贝叶斯定理，通过计算后验概率来进行分类决策。
基于朴素条件独立性假设，将样本的特征之间看作相互独立的，从而简化计算。
在训练阶段，朴素贝叶斯算法统计每个类别下各个特征的条件概率分布。
在预测阶段，根据观测到的特征值，利用贝叶斯定理计算后验概率，选择具有最大后验概率的类别作为预测结果。

用垃圾邮件的案例为例子：

3.2 MAP分类准则

朴素贝叶斯算法的MAP分类准则是一种基于贝叶斯定理和最大后验概率来进行分类的方法。在朴素贝叶斯算法中，MAP分类准则用于选择具有最大后验概率的类别作为预测结果。

因为变量相互独立，为方便公式标记，不妨记P(C=c|X=x)为P(c|x)，基于属性条件独立性假设，贝叶斯公式可重写为：

其中d为属性数目，x_i 为 x 在第i个属性上的取值。 

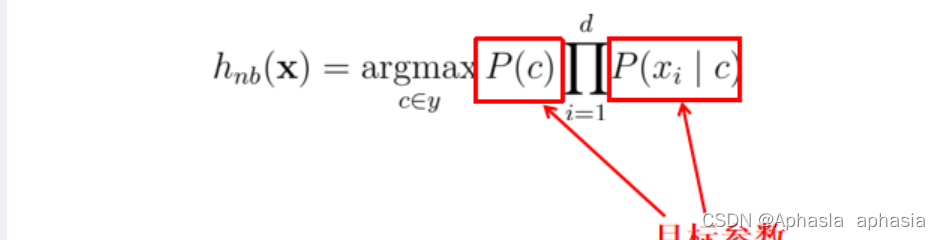
由于对所有类别来说 P(x)相同，因此MAP判定准则可改为：

3.3 拉普拉斯修正

拉普拉斯修正是指在计算概率时对每个计数都加上一个小的修正值，通常是1，以防止概率为零的情况出现。这样做可以避免因为某个特征在训练集中未出现而导致整个类别的概率为零的问题。
在朴素贝叶斯分类器中，拉普拉斯修正通过在每个类别的计数中加上一个常数来实现，以确保所有特征的概率不会为零。

则修改可为：

3.4 防溢出策略

在朴素贝叶斯算法中，条件概率的乘积往往涉及多个小于1的概率，这样的连乘运算容易导致下溢。为了避免这种情况，可以对概率进行取对数处理，将连乘转化为连加，同时也能够减少计算复杂度。

下面是采用对数变换的防溢出策略的一般步骤：

计算先验概率和条件概率时，对其取自然对数。
在预测时，对后验概率进行计算时同样取自然对数。
对类别的后验概率进行取对数处理后，选择具有最大对数后验概率的类别作为预测结果。
通过取对数处理，可以有效避免概率连乘时出现下溢或上溢的问题，提高了计算的稳定性和准确性

四、 垃圾邮箱的分类实现

4.1 构建给出的email和sogo数据集

import os

from utils import *
from collections import defaultdict

def build_email_dataset(language,root_dir = "dataset\\email"):
    
    dataset = {}
    category_cnt = {
        'ham':0,
        'spam':0
    }
    ham_dir = os.path.join(root_dir, 'ham')
    spam_dir = os.path.join(root_dir, 'spam')
    
    ham_vocabulary = defaultdict(int)
    spam_vocabulary = defaultdict(int)
    
    # use 20 ham + 20 spam as train dataset
    # use the rest as test dataset
    for file_name in os.listdir(ham_dir)[:-5]:
        #print('processing ham file:', file_name)
        category_cnt['ham'] += 1
        words = load_text(os.path.join(ham_dir,file_name),language)
        for word in words:
            if word.startswith('http') or word.startswith('www'):
                continue
            ham_vocabulary[word]+=1
    
    for file_name in os.listdir(spam_dir)[:-5]:
        #print('processing spam file:', file_name)
        category_cnt['spam'] += 1
        words = load_text(os.path.join(spam_dir,file_name),language)
        for word in words:
            if word.startswith('http') or word.startswith('www'):
                continue
            spam_vocabulary[word]+=1
    
    dataset['ham'] = ham_vocabulary
    dataset['spam'] = spam_vocabulary
    #print(ham_vocabulary)
    #print('ham vocabulary size:',len(ham_vocabulary)) # 421
    #print('spam vocabulary size:',len(spam_vocabulary))# 264
    dataset['category_cnt'] = category_cnt
    dataset['total_cnt'] = sum(category_cnt.values())
    
    test_set = {}
    for file_name in os.listdir(ham_dir)[-5:]:
        file_name = os.path.join(ham_dir,file_name)
        test_set[file_name] = 'ham'
    for file_name in os.listdir(spam_dir)[-5:]:
        file_name = os.path.join(spam_dir,file_name)
        test_set[file_name] = 'spam'
    
    #print(test_set)
    return dataset, test_set
       

def build_sougou_dataset(language, root_dir = "dataset\\SogouC"):
    
    dataset = {}
    category_cnt = {}
    
    test_set = {}
    
    classlist_path = os.path.join(root_dir, 'ClassList.txt')
    data_path = os.path.join(root_dir,'Sample')
    with open(classlist_path,'r',encoding='utf-8') as f:
        lines = f.readlines()
        for line in lines:
            class_dir, class_name = line.strip('\n').split('\t')
            dataset[class_name] = defaultdict(int)
            category_cnt[class_name] = 0
            for file_name in os.listdir(os.path.join(data_path,class_dir))[:-1]: # use the last file as test set
                category_cnt[class_name] += 1
                words = load_text(os.path.join(data_path,class_dir,file_name),language)
                for word in words:
                    dataset[class_name][word]+=1
    
            last_file = os.listdir(os.path.join(data_path,class_dir))[-1]
            last_file = os.path.join(data_path,class_dir,last_file)
            test_set[last_file] = class_name
    
    dataset['category_cnt'] = category_cnt
    #print(category_cnt)
    dataset['total_cnt'] = sum(category_cnt.values())
    
        
    return dataset, test_set

这段代码是用于构建电子邮件和搜狗数据集的函数。

build_email_dataset(language, root_dir)函数用于构建电子邮件数据集。它接受两个参数：

• language：指定文本语言的参数。
• root_dir：数据集所在的根目录，默认为"dataset\email"。

函数首先创建一个空的dataset字典来存储数据集，以及一个category_cnt字典来统计每个类别的样本数量。然后，它将指定的根目录下的"ham"文件夹和"spam"文件夹的路径进行拼接。接下来，函数使用load_text函数加载每个文件的文本数据，并将单词添加到对应类别的词汇表中。其中，ham_vocabulary和spam_vocabulary分别用于存储"ham"和"spam"类别的词汇表。

在处理完所有文件后，函数将最终的词汇表和样本数量信息保存到dataset字典中，并返回该字典作为训练数据集。另外一个数据集同这个。

4.2 定义移除常见停用词和特殊字符

# basic stop word set
stop_word_set = [',','.',':',';','(',')','[',']',
                     '{','}','<','>','/','\\','|','?'
                     ,'!','@','#','$','%','^','&','*',
                     '~','`','+','=','_','-','\n','\t','\r','&nbsp']

# chinese stop word set
stop_word_dir = 'dataset\\SogouC\\stopwords_cn.txt'
with open(stop_word_dir,'r',encoding='utf-8',errors='ignore') as f:
    stop_word_set_cn = f.read().split('\n')

def delete_stop_word(word,type='cn'):
    
    for stop_word in stop_word_set:
        word = word.replace(stop_word,'')
    for number in ['0','1','2','3','4','5','6','7','8','9']:
        word = word.replace(number,'')
   
    
    # delete the english character in chinese text
    if type == 'cn':
        for i in range(26):
            word = word.replace(chr(ord('a')+i),'')
            word = word.replace(chr(ord('A')+i),'')
        word = word.replace(' ','')
        # remove chinese character
        for c in ['。','，','：','；','（','）','【','】',
              '{','}','<','>','/','\\','|','？','！',
              '@','#','$','%','^','&','*','~','`','+','=','_','-','、']:
            word = word.replace(c,'')
        
    return word

def load_text(file_path,file_type='en',total = False):

    with open(file_path,'r',encoding='utf-8',errors='ignore') as f:
        if total:
            return f.read()
        content = f.read().replace(' ','')
        
    return delete_stop_word(content,file_type)

首先，定义了英文停用词集合stop_word_set，其中包括了常见的标点符号和空白字符等。同时，还定义了中文停用词集合stop_word_set_cn，它通过读取文件"dataset\SogouC\stopwords_cn.txt"来获取中文停用词列表。

接下来是delete_stop_word(word, type='cn')函数，用于删除停用词和特殊字符。最后是load_text(file_path, file_type='en', total=False)函数，用于加载文本数据并进行处理。

4.3 构建朴素贝叶斯分类器

import argparse
from time import sleep
import math
from dataset import *

def main(args):
    
    LANGUAGE = 'en'
    
    if args.email:
        LANGUAGE = 'en'
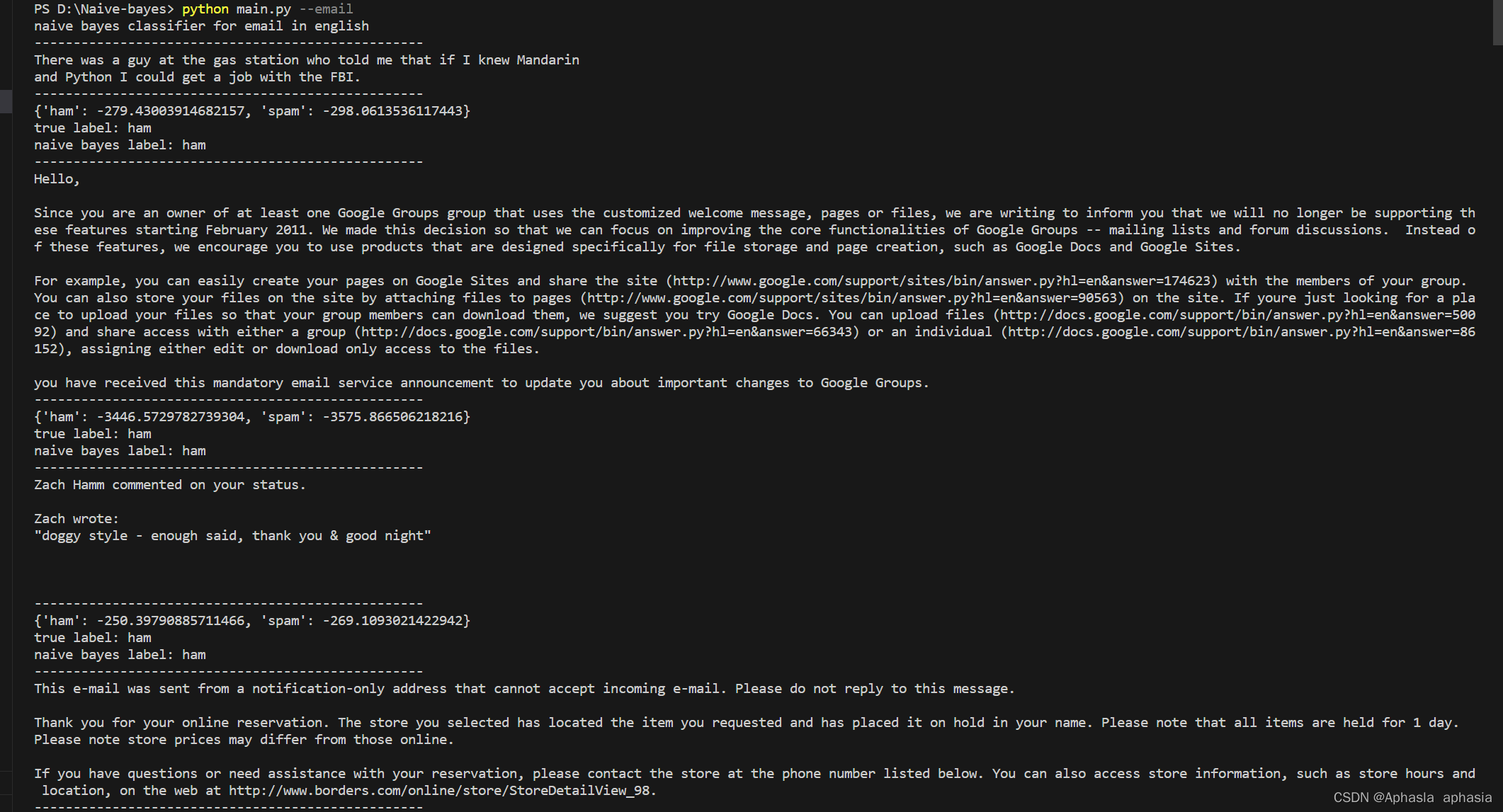
        print('naive bayes classifier for email in english')
        # dataset construction:
        # ham_vocabulary, spam_vocabulary, test_set = build_email_dataset()
        dataset,test_set = build_email_dataset(language=LANGUAGE)
    elif args.sougou:
        LANGUAGE = 'cn'
        print('naive bayes classifier for sougou in chinese')
        dataset,test_set = build_sougou_dataset(language=LANGUAGE)
        
    else :
        print('please specify the dataset')
        return

    # test
    total = 0
    correct = 0

    for file_path in test_set:
        words = load_text(file_path,LANGUAGE,total=True)
        
        # print split line
        print('-'*50)
        print(words)
        print('-'*50)
        true_label = test_set[file_path]
        naive_bayes_label = calculate_naive_bayes(dataset,load_text(file_path,LANGUAGE))
        print('true label:',true_label)
        print('naive bayes label:',naive_bayes_label)
        if naive_bayes_label == true_label:
            correct += 1
        total += 1

    print(f'accuracy: {100*correct/total} %')



def calculate_naive_bayes(dataset,words):

    possibility = {}
    for class_name,category_cnt in dataset['category_cnt'].items():
        possibility[class_name] = math.log(category_cnt/dataset['total_cnt'])
    
    #print(possibility)
    
    class_names = dataset['category_cnt'].keys()
    
    for word in words:
        for class_name in class_names:
            total_word_number = sum(dataset[class_name].values())
            # print('total word number:',total_word_number)
            # print(word)
            # exit(0)
            if word in dataset[class_name].keys():
                #print("find word:",word)
                possibility[class_name] += math.log((dataset[class_name][word]+1)/(total_word_number+len(dataset[class_name])))
                #print('possibility:',possibility)
                #sleep(3)
            else:
                possibility[class_name] += math.log(1/(total_word_number+len(dataset[class_name])+1))
    
    #possibility = np.softmax(possibility)
    print(possibility)
    label = max(possibility,key=possibility.get)
    return label


if __name__ == '__main__':
    parser = argparse.ArgumentParser()
    parser.add_argument('--email',action='store_true')
    parser.add_argument('--sougou',action='store_true')
    args = parser.parse_args()
    main(args)

    

首先，通过argparse模块解析命令行参数。可以使用--email参数指定使用英文邮件数据集，或者使用--sougou参数指定使用中文搜狗数据集。

接下来，根据参数选择相应的数据集构建函数和语言类型。如果使用--email参数，则调用build_email_dataset函数构建英文邮件数据集；如果使用--sougou参数，则调用build_sougou_dataset函数构建中文搜狗数据集。同时，将测试集保存到test_set变量中。

然后，使用循环遍历测试集中的每个文件路径。通过load_text函数加载文本数据，并将整篇文本传递给calculate_naive_bayes函数进行分类。然后将真实标签和朴素贝叶斯分类结果打印出来，并统计分类准确率。

4.4 算法的用法和输出

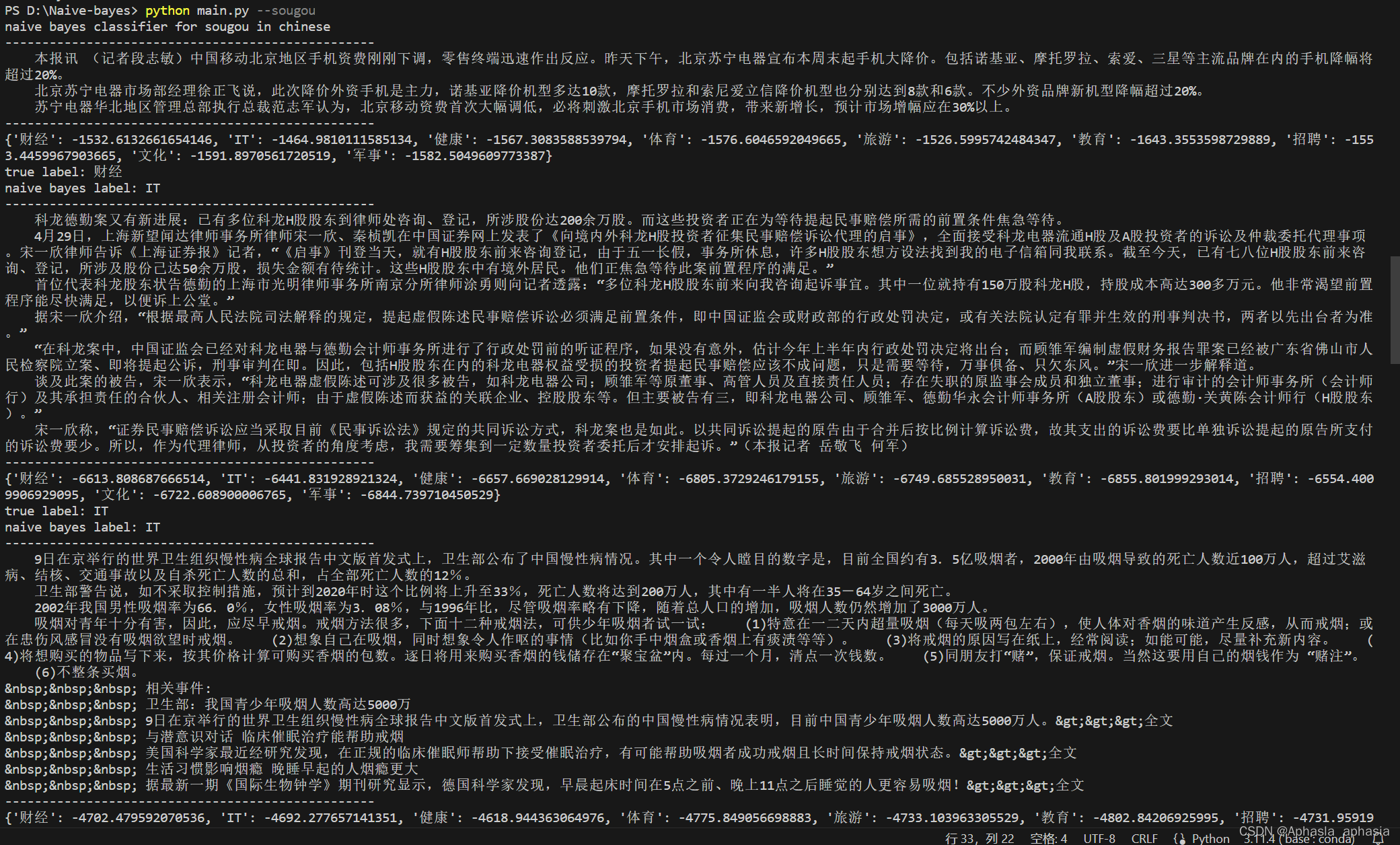
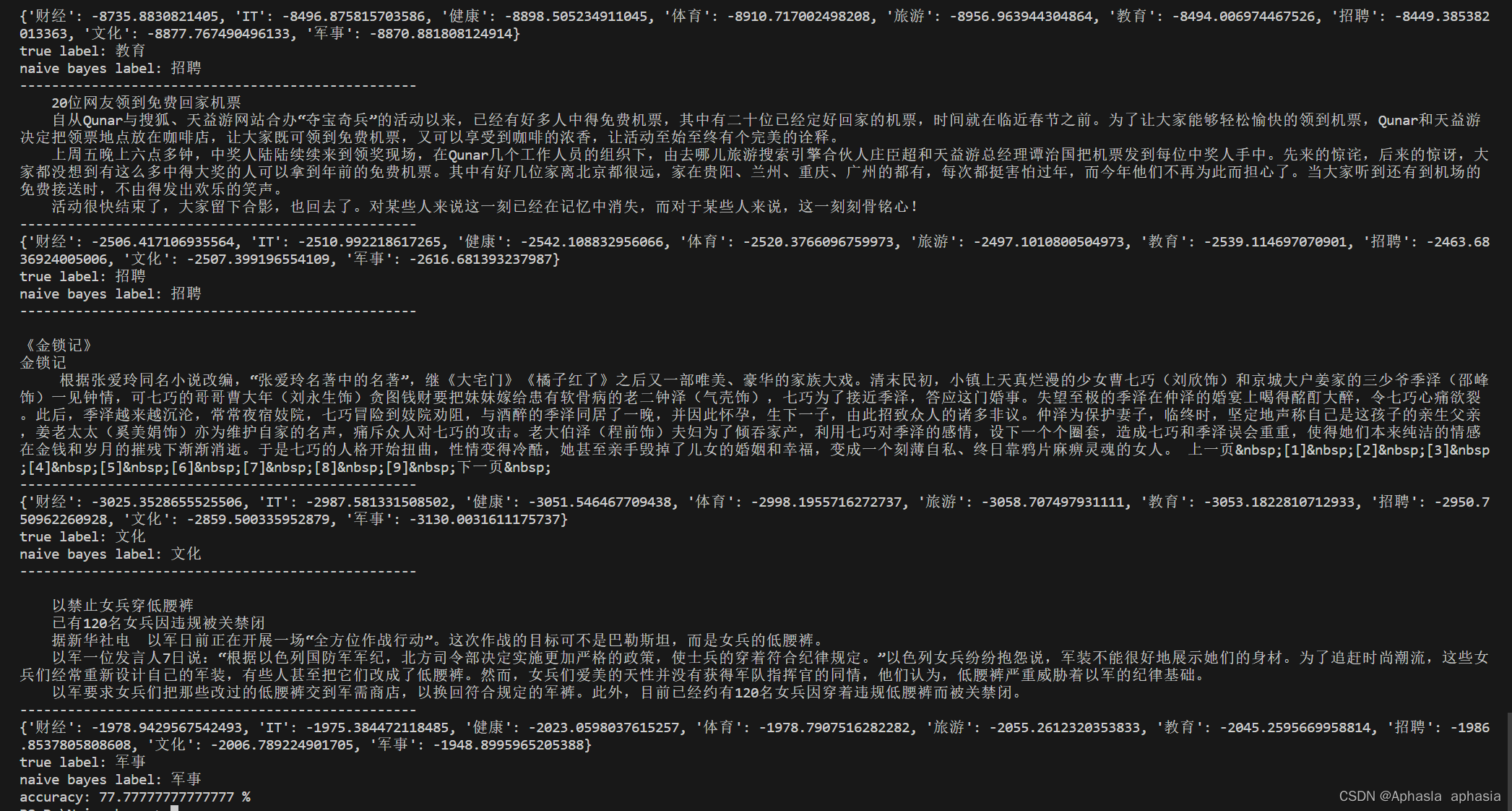
截取重点，部分输出省略 

五、实验小结

5.1 朴素贝叶斯的优缺点

优点：

算法逻辑简单,易于实现
分类过程中时空开销小
缺点：

理论上，朴素贝叶斯模型与其他分类方法相比具有最小的误差率。但是实际上并非总是如此，这是因为朴素贝叶斯模型假设属性之间相互独立，这个假设在实际应用中往往是不成立的，在属性个数比较多或者属性之间相关性较大时，分类效果不好.
而在属性相关性较小时，朴素贝叶斯性能最为良好。对于这一点，有半朴素贝叶斯之类的算法通过考虑部分关联性适度改进.

5.2 实验中的心得体会

• 首先先验集并不是从一个大样本中筛选出来的,所以导致每一个类的初始先验概率相同.事实上垃圾邮件的数量会多于正常邮件,搜狗中也并不是这九个类的先验概率相同,这显然是不合理的.
• 其次如果真的完全按照朴素贝叶斯公式来计算也是存在问题的,因为朴素贝叶斯公式是要求各个特征的概率值相乘,多个(0~1)且接近0的小数相乘很容易造成python的下溢出,导致概率归0.

  • 解决方法为利用 math.log 函数的性质,单调递增,内部的乘积可以转化为外部的加法

    

    把概率的累乘变为多个log的累加,且由于单调递增的性质不会对结果造成影响