225.用队列实现栈

请你仅使用两个队列实现一个后入先出（LIFO）的栈，并支持普通栈的全部四种操作（push、top、pop 和 empty）。

实现 MyStack 类：

void push(int x) 将元素 x 压入栈顶。
int pop() 移除并返回栈顶元素。
int top() 返回栈顶元素。
boolean empty() 如果栈是空的，返回 true ；否则，返回 false 。

思路:用队列实现栈，首先要清楚队列和栈两者数据结构的区别:队列是先进先出的结构，栈是先进后出的。如果想用队列实现栈较为简单，只需要定义一个栈即可，看pop()函数，想要移除并返回栈顶元素，栈顶元素是队列的尾部元素，所以先用一个变量存储队列的长度，减一是为了让下一个队列的队头为栈顶元素，记录栈顶元素，移除，返回；top函数的话可以直接调用已经实现的pop函数进行操作，只不过不要移除，所以要在压回队列内。

class MyStack {
public:
   queue<int> que;
    MyStack() {
    }
    void push(int x) {
        que.push(x);
    }
    int pop() {
        int size=que.size();
        size=size-1;
        while(size--){
            que.push(que.front());
            que.pop();
        }
        int val=que.front();
        que.pop();
        return val;
    }
    int top() {
        int val=pop();
        que.push(val);
        return val;
    }
    bool empty() {
        if(que.empty()){
            return true;
        }
        return false;
    }
};

232.用栈实现队列

请你仅使用两个栈实现先入先出队列。队列应当支持一般队列支持的所有操作（push、pop、peek、empty）：

实现 MyQueue 类：

void push(int x) 将元素 x 推到队列的末尾
int pop() 从队列的开头移除并返回元素
int peek() 返回队列开头的元素
boolean empty() 如果队列为空，返回 true ；否则，返回 false

 思路:实现队列的话可不能只用一个栈了，要用到两个栈，一个是输出栈，一个是输入栈。

class MyQueue {
public:
    MyQueue() {
    }
    stack<int> st1;//输入栈
    stack<int> st2;//输出栈
    void push(int x) {
      while(!st2.empty()){
        st1.push(st2.top());
        st2.pop();
      }
      st1.push(x);
    }
    int pop() {
        while(!st1.empty()){
          st2.push(st1.top());
          st1.pop();
        }
        int val=st2.top();
        st2.pop();
        return val;
    }
    int peek() {
         while(!st1.empty()){
          st2.push(st1.top());
          st1.pop();
        }
        int val=st2.top();
        return val;
    }
    bool empty() {
        if(st1.empty()&&st2.empty()){
            return true;
        }
        return false;
    }
};

92.链表内指定区间反转

为明天面试做准备的算法题，感觉挺有难度的

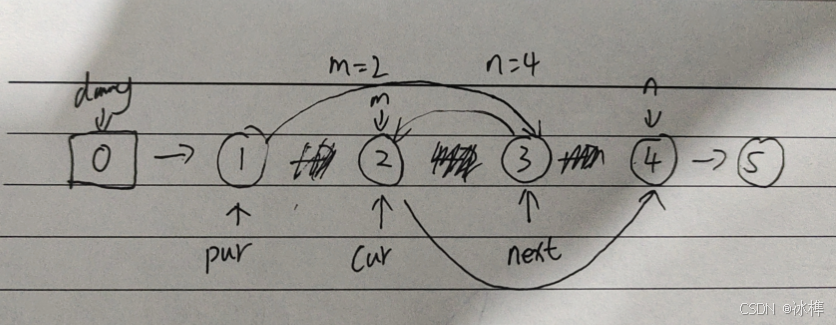
 思路:首先判断，当头节点不为空且两位置相等时，返回头节点，然后，由于我们可能要操作头节点，所以要定义一个虚拟头节点来方便对头节点的操作，之后，定义一个节点pur,让他指向要操作节点的前一个结点，定义一个cur节点指向pur的下一个节点，然后进入循环，让next节点指向cur节点的下一个节点，然后将cur节点指向下一个节点的下一个节点，然后让next节点指向pur的下一个节点，(因为需要让pur指向已经反转之后的开头节点)，然后让pur->next=next;,这样就将pur节点指向了next节点，第一次反转成功，第二次流程如上。

class Solution {
public:
    ListNode* reverseBetween(ListNode* head, int m, int n) {
        // write code here
        if(head!=nullptr&&n==m){
            return head;
        }
        ListNode* dummy=new ListNode(0);
        dummy->next=head;
        ListNode* pur=dummy;
       for(int i=1;i<m;i++){
        pur=pur->next;
       }
        ListNode* cur=pur->next;
        ListNode* next;
        int size=n-m;
        while(size--){
            next=cur->next;
            cur->next=cur->next->next;
            next->next=pur->next;
            pur->next=next;
        }
        return dummy->next;
    }
};

104.计算二叉树的最大深度

给定一个二叉树 root ，返回其最大深度。

二叉树的 最大深度 是指从根节点到最远叶子节点的最长路径上的节点数。

 思路:本题目较为简单，通过深度优先搜索就可以算出，每次返回值是左右最大深度加上头节点。

class Solution {
public:
    int maxDepth(TreeNode* root) {
        if(root==nullptr){
            return 0;
        }
      int leftmax=maxDepth(root->left);
       int rightmax= maxDepth(root->right);
        return leftmax>rightmax?leftmax+1:rightmax+1;
    }
};

落下三道题了，周日在补上吧😭