Bootstrap

七大排序——纯C

🎆前言🎆

✨笔者也仅是大一萌新，写博客为了记录和巩固知识✨

🥰赠人玫瑰，手留余香，欢迎各位读者进行交流和建议🥰

🌹能与大家一起学习，一起进步是我的荣幸🌹

🤞如果这篇文章有帮助到您，还请留个赞支持一下哦🤞

1

1.排序的概念:

排序:所谓排序，就是使一串记录，按照其中的某个或某些关键字的大小，递增或递减的排列起来的操作。
稳定性:即排序前后排序后，相同数据前后次序没有发生改变，即:1 2 3 2这一组数据，排序后为:1 2 2 3，红色的2依旧在绿色的2之前，那么就可以说这种排序方法是稳定的
内部排序:数据元素全部放在内存中的排序。
外部排序:数据元素太多不能同时放在内存中，根据排序过程的要求不能在内外存之间移动数据的排序。

2.常见的排序:

插入排序:直接插入排序 希尔排序

选择排序:选择排序 堆排序

交换排序:快速排序 冒泡排序

归并排序:归并排序

前期准备:

打印和交换:

void PrintArray(int* a, int n) //打印函数
{
	for (int i = 0; i < n; i++)
	{
		printf("%d ", a[i]);
	}
	printf("\n");
}
void Swap(int* pa, int* pb) //交换函数
{
	int tmp = *pa;
	*pa = *pb;
	*pb = tmp;
}

函数声明:

#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#include <string.h>

void PrintArray(int* a, int n);
//插入
void InsertSort(int* a, int n);
//希尔
void ShellSort(int* a, int n);

//直接选择
void SelectSort(int* a, int n);

//堆排序
void AdjustDown(int* a, int n, int root);
void HeapSort(int* a, int n);

//冒泡排序
void BubbleSort(int* a, int n);

//快排
void QuickSort(int* a, int begin, int end);
void QuickSort2(int* a, int begin, int end);

//非递归快排
void QuickSort3(int* a, int begin, int end);
//归并
void MergeSort(int* a, int n);
//非递归归并
void MergeSortNonR(int* a, int n);
//计数排序
void CountSort(int* a, int n);

插入排序:

直接插入排序:

特性：

  1. 越接近有序，它的时间效率越高
  2. 时间复杂度:O(N2) 空间复杂度:O(1)
  3. 稳定性:稳定(当它们相等时不做变动，所以稳定)

思路：

类似于我们斗地主理牌

b8c9361310434da191b3b3ea86ca89e2_th

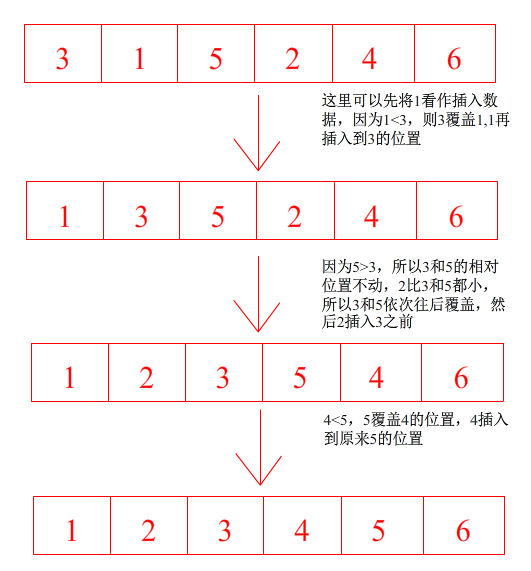
我们每插入一个元素，就会对它进行排序，使其变成有序，此时，在插入这个元素之前的所有元素都是有序的，那么我们从第一个元素开始就让它有序，之后每一个元素，都进行一次排序，下图从3开始就是第一个有序元素，按升序来排，如果1<3，那么就进行覆盖(类似于顺序表的头插)

image-20220507231022735

image-20220507232814168

void InsertSort(int* a, int n)
{
	for(int i = 0; i < n - 1; i++) //进行n-1趟(因为后面要记录[end+1]的元素，防止越界就只能进行n-1次排序)
	{
		int end = i; //每一次for循环，end就到了下一个元素
		int tmp = a[end + 1]; //tmp记录end的下一个元素，防止该元素被覆盖后找不到
		while(end >= 0) //只要end不为负就继续循环单趟排序
		{
			if(tmp < a[end]) //升序，如果后一个插入的元素小于前一个，就进行覆盖
			{
				a[end + 1] = a[end]; //覆盖
				--end; //移动end到上一个元素
			}
			else //已经排好序的话，这趟就直接跳出，进行下一趟排序
			break;
		}
		a[end + 1] = tmp; //将记录的元素重新插入到数组中
	}
}
希尔排序:

插入排序的时间复杂度为O(N2) ，这并不算快，但是插入排序有个特性是:当它越接近有序，那么就越快，所以一位名叫希尔(Donald Shell)对其进行了优化，使得有了今天的希尔排序(又称"缩小增量排序")

特性：

  1. 是针对直接插入排序的优化(预排序优化)
  2. 时间复杂度(约为):O(N1.3) 空间复杂度:O(1)
  3. 稳定性:不稳定(可能被分在不同的gap组，此时分组排可能会让后面的排在前面)
  4. gap越小，越接近有序；gap越大，预排越快

思路:

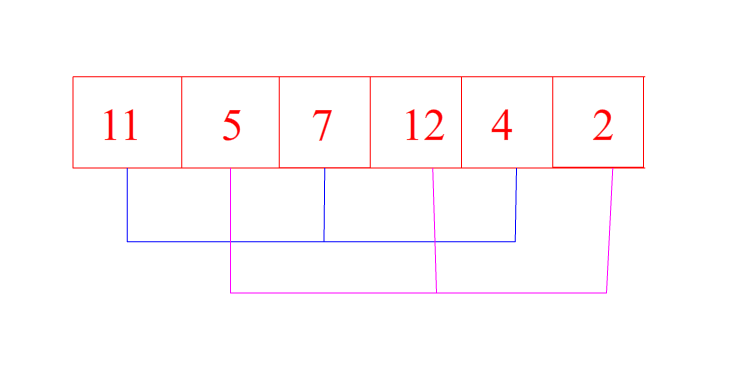
将一组元素分为gap组(gap一般为元素个数的1/2或者1/3)，然后对每一组进行排序，当gap等于1时预排序完成，此时为直接插入排序

如图:

将这组元素分为两组，先进行11 7 4的排序，再进行5 12 2排序，然后gap/2

image-20220509235416959

下图是预排序后的数组，此时gap为1，变为直接插入排序，经过预排后更加有序，速度也会更快

image-20220509235555056

void ShellSort(int* a, int n)
{
    //两层控制
	int gap = n;
    while(gap > 1)
    {
        gap = gap / 2; //这里如果要除3需要加个1，必须要gap最终为1，为1就是直接插入，但是经过了预排将快很多
        for(int i = 0; i < n - gap; i++) //控制整个排序，从第一个元素开始，到n-gap结束
        {
            int end = i;
            int tmp = a[end + gap];
            while(end >= 0)
            {
                if(tmp < a[end])
                {
                    a[end + gap] = a[end]; //覆盖
                    end -= gap; //覆盖后end再去找前面的元素
                }
                else
                    break;
            }
            a[end + gap] = tmp; //将记录元素插入进去
        }
    }
}

选择排序:

直接选择排序:
void SelectSort(int* a, int n)
{
    int left = 0, right = n - 1;
    while(left < right)
    {
        int maxi = left, mini = left;
        for(int i = left + 1; i <= right; i++)
        {
            if(a[i] < a[mini])
            {
                mini = i;
            }
            if(a[i] > a[maxi])
            {
                maxi = i;
            }
        }
        Swap(&a[left], &a[mini]);
        if(maxi == left)
        {
            maxi = mini;
        }
        Swap(&a[right], &a[maxi]);
        left++;
        right--;
    }
}
堆排序:
void AdjustDown(int* a, size_t size, size_t root)
{
    size_t parent = root;
    size_t child = parent * 2 + 1;
    while(child < size)
    {
        if(child + 1 < size && a[child] < a[child + 1])
        {
            child++;
        }
        if(a[child] > a[parent])
        {
            Swap(&a[child], &a[parent]);
            parent = child;
            child = parent * 2 + 1;
        }
        else
            break;
    }
}
void HeapSort(int* a, int n)
{
    for(int i = (n - 1 - 1) / 2; i >= 0; i--)
    {
        AdjustDown(a, n, i);
    }
    size_t end = n - 1;
    while(end > 0)
    {
        Swap(&a[0], &a[end]);
        AdjustDown(a, end, 0);
        --end;
    }
}

交换排序:

冒泡排序:
void BubbleSort(int* a, int n)
{
    for(int i = 0; i < n - 1; i++)
    {
        for(int j = 0; j < n - i - 1; j++)
        {
            if(a[j] > a[j + 1])
            {
                int tmp = a[j];
                a[j] = a[j + 1];
                a[j + 1] = tmp;
            }
        }
    }
    //优化版本,当冒泡有序时，将不会再次排序
	for (int i = 0; i < n; i++)
	{
		int flag = 0;
		for (int j = 1; j < n - i; j++)
		{
			
			if (a[j - 1] > a[j])
			{
				flag = 1;
				Swap(&a[j - 1], &a[j]);
			}
		}
		if (flag == 0)
			break;
	}
}
快速排序:

Hoare法:

int PartSort(int* a, int left, int right)
{
	int keyi = left;
	while(left < right)
	{
		while(left < right && a[right] >= a[keyi])
		{
			right--;
		}
		while(left < right && a[left] <= a[keyi])
		{
			left++;
		}
		Swap(&a[left], &a[right]);
	}
	Swap(&a[left], &a[keyi]);
	return left;
}
void QuickSort(int* a, int begin, int end)
{
	if(begin >= end)
	return;
	int keyi = PartSort(a, begin, end);
	QuuickSort(a, begin, keyi - 1);
	QuickSort(a, keyi + 1, end);s
}

归并排序：

归并排序:
void _MergeSort(int* a, int begin, int end, int* tmp)
{
	if (begin >= end)
		return;

	int mid = (begin + end) / 2;
	// [begin, mid][mid+1, end]
	_MergeSort(a, begin, mid, tmp);
	_MergeSort(a, mid + 1, end, tmp);

	// 归并[begin, mid][mid+1, end]
	//printf("归并[%d,%d][%d,%d]\n", begin, mid, mid+1, end);
	int begin1 = begin, end1 = mid;
	int begin2 = mid + 1, end2 = end;
	int index = begin;
	while (begin1 <= end1 && begin2 <= end2)
	{
		if (a[begin1] < a[begin2])
			tmp[index++] = a[begin1++];
		else
			tmp[index++] = a[begin2++];
	}

	while (begin1 <= end1)
		tmp[index++] = a[begin1++];

	while (begin2 <= end2)
		tmp[index++] = a[begin2++];

	memcpy(a + begin, tmp + begin, (end - begin + 1) * sizeof(int));
}

//时间:O(N*logN) 空间:O(N)
void MergeSort(int* a, int n)
{
	int* tmp = (int*)malloc(sizeof(int) * n);
	assert(tmp);

	_MergeSort(a, 0, n - 1, tmp);

	free(tmp);
}

void MergeSortNonR(int* a, int n)
{
	int* tmp = (int*)malloc(sizeof(int) * n);
	int gap = 1;

	while (gap < n)
	{
		// 间距为gap是一组，两两归并
		for (int i = 0; i < n; i += 2 * gap)
		{
			int begin1 = i, end1 = i + gap - 1;
			int begin2 = i + gap, end2 = i + 2 * gap - 1;
			// end1 越界，修正
			if (end1 >= n)
				end1 = n - 1;

			// begin2 越界，第二个区间不存在
			if (begin2 >= n)
			{
				begin2 = n;
				end2 = n - 1;
			}

			// begin2 ok， end2越界，修正end2即可
			if (begin2 < n && end2 >= n)
				end2 = n - 1;

			// 条件断点
			if (begin1 == 8 && end1 == 9 && begin2 == 9 && end2 == 9)
			{
				int x = 0;
			}

			printf("归并[%d,%d][%d,%d]\n", begin1, end1, begin2, end2);

			int index = i;
			while (begin1 <= end1 && begin2 <= end2)
			{
				if (a[begin1] < a[begin2])
					tmp[index++] = a[begin1++];
				else
					tmp[index++] = a[begin2++];
			}

			while (begin1 <= end1)
				tmp[index++] = a[begin1++];

			while (begin2 <= end2)
				tmp[index++] = a[begin2++];
		}
		memcpy(a, tmp, n * sizeof(int));

		gap *= 2;
	}
	free(tmp);
}

悦读

道可道，非常道；名可名，非常名。 无名，天地之始，有名，万物之母。 故常无欲，以观其妙，常有欲，以观其徼。 此两者，同出而异名，同谓之玄，玄之又玄，众妙之门。

最新收录
Linux：进程终止
2024年有多少程序员转行了？
Mybatis @Flush注解分析
[leetcode]151. Reverse Words in a String
苹果微信分身双开以及多开教程！方法教程来了！
ENVI5.3.1 去除影像四周的黑色背景
06.sqlite3学习——DQL（数据查询）（全）
查询计算机会议信息一站式工具：截稿日期、召开信息、会议等级全都有！
疫情下的大数据力量：多地政府借力大数据技术，多家企业上马大数据产品
华为2023年提出的多元时间序列预测模型（MTS-Mixers）
;