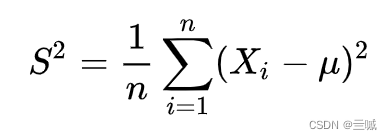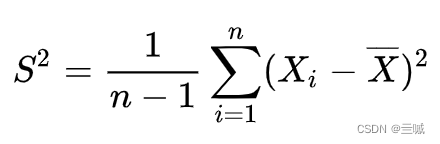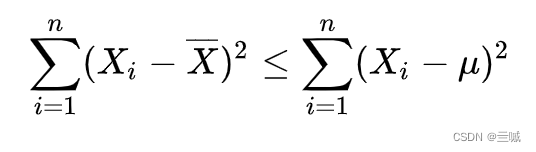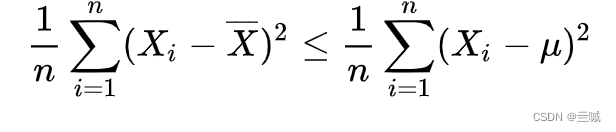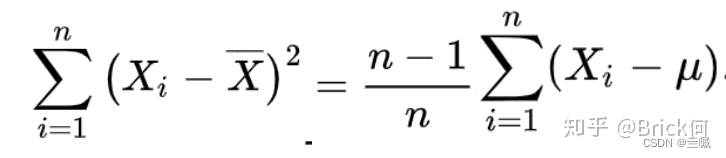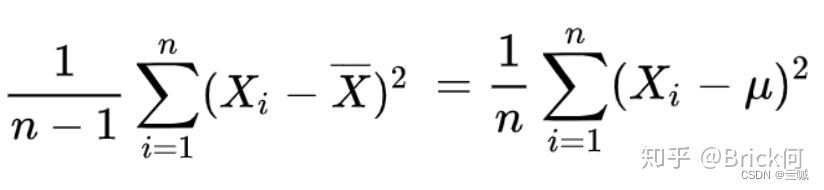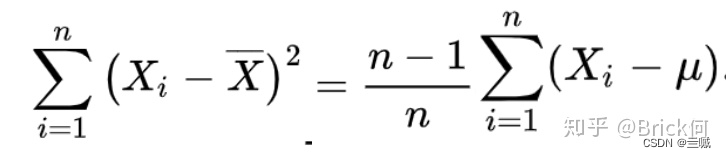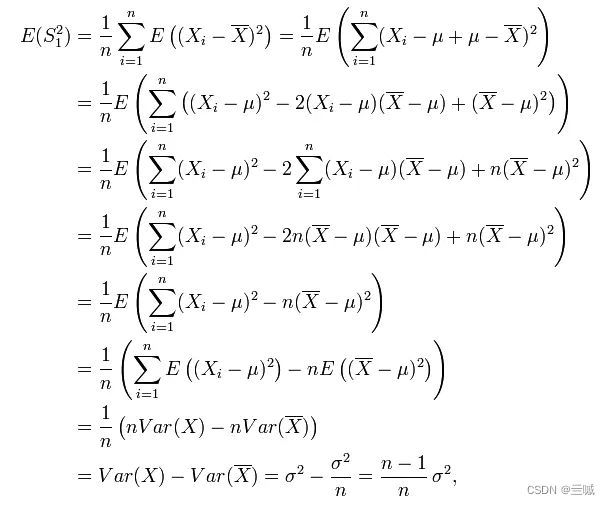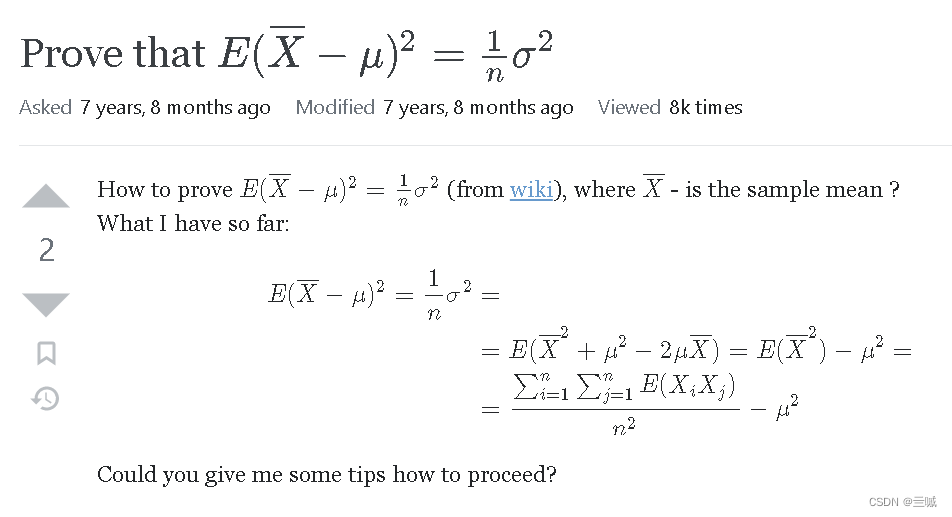方差概念
除以n其实没错,但只适用于母体方差(总体均数已知);
同样的,样本标准差也只适用于样本方差。
让我们看一下这两个公式:
统计学重要的研究内容之一是“用样本推测总体”。具体而言,就是用样本均数和样本标准差来估计总体均数和总体标准差,而这里的估计有一个很重要的原则就是“无偏”。所谓“无偏”,就是说,样本值应该是围绕总体值上下波动的,它不能总在总体值的上面,或者总在总体值下面。这里我们需要明确,对于一个特定的总体,其总体均数和总体标准差是恒定不变的。但是,从总体中我们可以进行无数次抽样,每次抽样便获得一个特定的样本,然后计算出特定的样本均数和样本标准差。所以,只要抽样一次,样本值就可能变化一次。因此,样本值是变化的。用一个变化的量去估计一个恒定的量,首要原则就是“无偏”。换言之,如果我们知道某一个变化的量如果总是小于这个恒定的量,那么这个变化量就不是一个无偏估计。
比如:
为了实现无偏,得到下面这个公式(右边少个平方):(推导在问题一)
变换一下得到我们最初问题的答案:
问题一
让我们深入探究一下这个公式(右边少个平方)怎么推导出来的:
但还是有些问题,比如倒数第二行是如何推导出最后一行的(推导在问题二)。
问题二
我们可以看一下一个问题及它的两个答案来梳理一下:
问题:
它的两个答案:
第一个:
第二个:
经过这两个答案的解释,我想你应该理会的差不多了,若还有问题请@我,希望你能考倒我。
对了你可以通过观察正态分布来加深印象,毕竟公式太枯燥了。
个人小结
其实我对s的平方和与θ的平方和有过疑惑,其实两者的关系十分简单:
奇技淫巧
我不太清楚对错,也没太看懂,但这个思路很奇特。