1.快速排序

使用条件：必须是”顺序表“，即“数组”。乱序

快排优势：时间复杂度低，代码简洁。

int huafen (int A[],int L,int R){
    int mid = A[L];//选择最左边的作为枢轴
    while(L<R){
        while(A[R]>=mid && L<R) R--;
        A[L]=A[R];
        while(A[L]<=mid && L<R) L++;
        A[R]=A[L];
    }
    A[L]=mid;
    return L;//返回划分的中点位置
}
void Qsort(int A[],int L,int R){
    if(L>=R) return;//递归终止
    int M=huafen(A,L,R);
    Qsort(A,L,M-1);//左半部分快排
    Qsort(A,M+1,R);//右半部分快排
}

11分

int huafen (int A[],int L,int R){
    int mid = A[L];//选择最左边的作为枢轴
    while(L<R){
        while(A[R]>=mid && L<R) R--;
        A[L]=A[R];
        while(A[L]<=mid && L<R) L++;
        A[R]=A[L];
    }
    A[L]=mid;
    return L;//返回划分的中点位置
}
void Qsort(int A[],int L,int R){
    if(L>=R) return;//递归终止
    int M=huafen(A,L,R);
    Qsort(A,L,M-1);//左半部分快排
    Qsort(A,M+1,R);//右半部分快排
}
int func(int A[],int N,int B[],int M){
    int C[N+M];
    for(int i=0;i<N;i++){
        C[i]=A[i];
    }
    for(int i=0;i<M;i++){
        C[i+N]=B[i];
    }
    Qsort(C,0,N+M-1);//对数组使用快排
    return C[(N+M-1)/2];//返回中位数
}

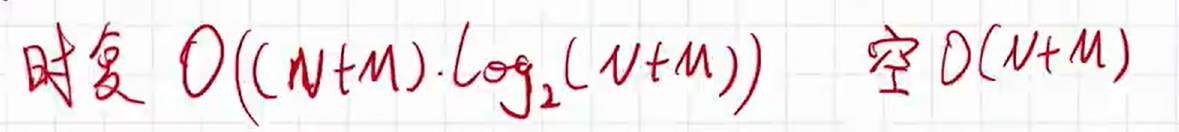
为什么空间复杂度不是log₂ (n+m)?

因为我们定义的C数组大于log ₂(n+m)。

12分

int Merge(int A[],int n,int B[],int m,int C[]){
    int i=0,j=0,k=0;
    while(i<n && j<m){
        if(A[i]<=B[j]) C[k++]=A[i++];
        else C[k++]=B[j++];
    }
    while(i<n) C[k++]=A[i++];
    while(j<m) C[k++]=B[j++];
    return 1;
}
int func(int A[],int n,int B[],int m){
    int C[n+m];
    Merge(A,n,B,m,C);
    return C[(n+m)/2];
}

Merge 操作的空间复杂度为O(n)。

一趟Merge（归并）的时间复杂度为O(n)。

int huafen (int A[],int L,int R){
    int mid = A[L];//选择最左边的作为枢轴
    while(L<R){
        while(A[R]>=mid && L<R) R--;
        A[L]=A[R];
        while(A[L]<=mid && L<R) L++;
        A[R]=A[L];
    }
    A[L]=mid;
    return L;//返回划分的中点位置
}
void Qsort(int A[],int L,int R){
    if(L>=R) return;//递归终止
    int M=huafen(A,L,R);
    Qsort(A,L,M-1);//左半部分快排
    Qsort(A,M+1,R);//右半部分快排
}
int func(int A[],int N){
    Qsort(A,0,N-1);
    int n=A[N/2];
    int count=0;
    //for(int i=0;i<N;i++){
    //    if(n==A[i]){
    //        count++;
    //    }
    //}//以下是王道的答案；
    for(int i=N/2;i>=0;i--){
        if(n==A[i]){
            count++;
        }
    }
    for(int i=N/2-1;i<N;i++){
        if(n==A[i]){
            count++;
        }
    }
    if(count>N/2){
        return n;
    }else{
        return -1;
    }
}

时间复杂度和空间复杂度就是快速排序的时间复杂度和空间复杂度。

int huafen (int A[],int L,int R){
    int mid = A[L];//选择最左边的作为枢轴
    while(L<R){
        while(A[R]>=mid && L<R) R--;
        A[L]=A[R];
        while(A[L]<=mid && L<R) L++;
        A[R]=A[L];
    }
    A[L]=mid;
    return L;//返回划分的中点位置
}
void Qsort(int A[],int L,int R){
    if(L>=R) return;//递归终止
    int M=huafen(A,L,R);
    Qsort(A,L,M-1);//左半部分快排
    Qsort(A,M+1,R);//右半部分快排
}
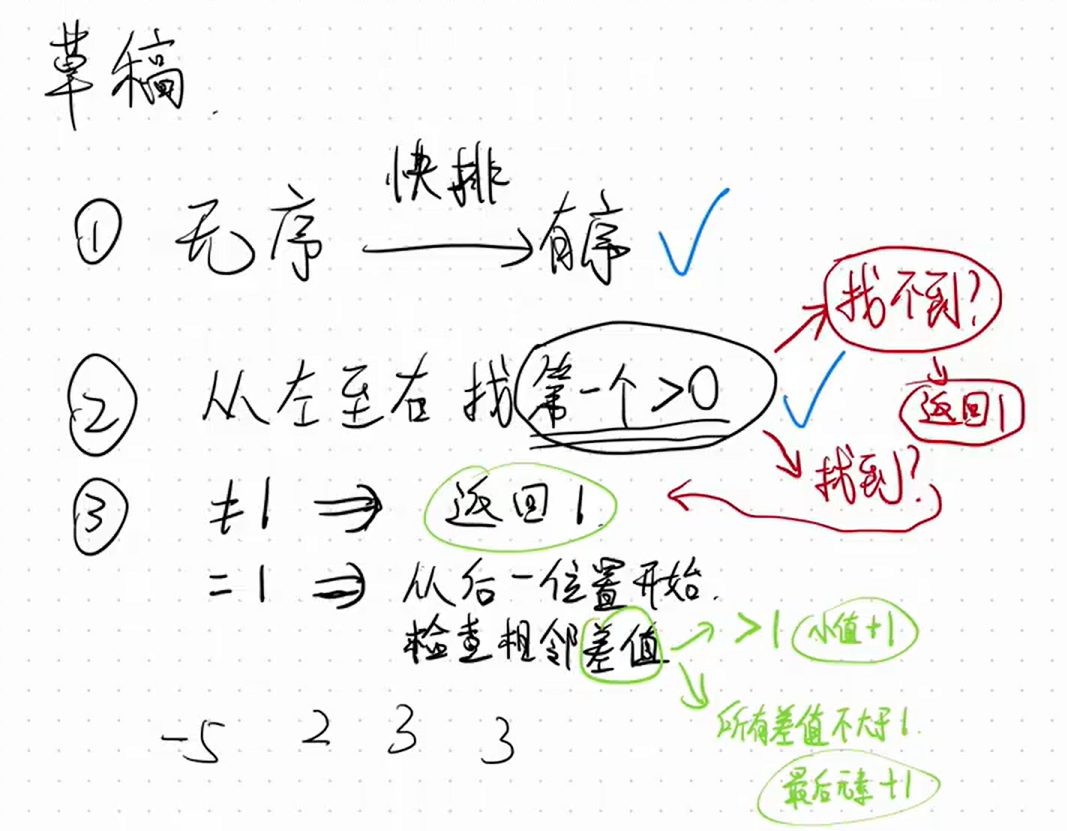
int func(int A[],int n){
    Qsort(A,0,n-1);
	int m =-1;
	for(int i=0;i<n;i++){
  	  if(A[i]>0){
  	      m = i;	
   	     break;
 	   }
	}
	if(m == -1) return 1;//如果m等于-1说明，数组A全都是小于0
	if(A[m] != 1) return 1;//如果能走到下一条语句，说明A[m]等于1，无须再判断
	for(m=m+1;m<n;m++){
	    if(A[m]-A[m-1]>1){
	        return A[m-1]+1;//作差后大于1，则返回小的加1
 	   }
	}
	return A[n-1]+1;//返回最后一个值加1，此时数组A所有元素均是紧挨着的
}

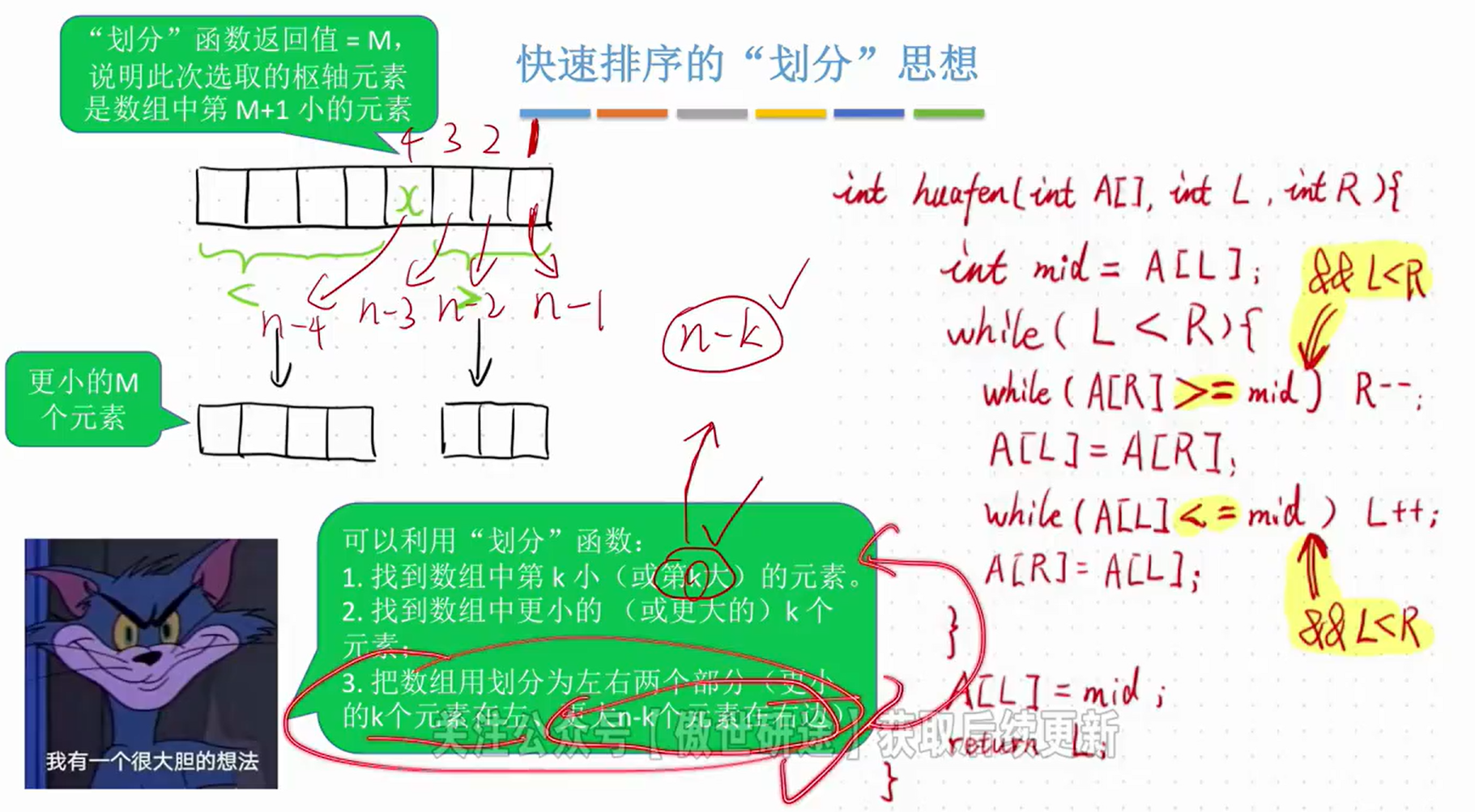
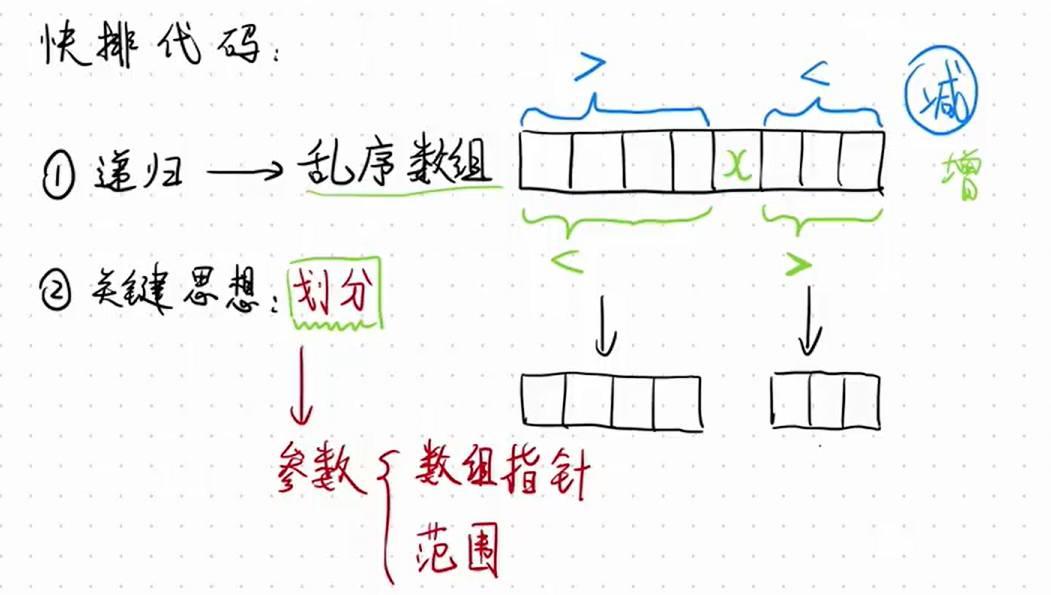
2.划分思想

第K小（或第K大）可理解为，排好序之后的位置，因为数组排好序之后位置与数组下标是有对应关系的；

int huafen (A[],int L,int R){
    int mid=A[0];//选择枢轴
    while(L<R){
        while(A[R]>=mid && L<R) R--;
        A[L]=A[R];
        while(A[L]<=mid && L<R) L++;
        A[R]=A[L];
    }
    A[L]=mid;//划分位置的值
    return L;//返回划分的位置
}
int func(int A[],int n,int K){//找到第K小的元素
    int L=0,R=n-1,M=0;
    while(1){
        M = huafen(A,L,R);
        if(M==K-1) break;
        else if(M > K-1) R=M-1;
        else if(M < K-1) L=M+1;
    }
    return A[K-1];
}

int huafen (A[],int L,int R){
    int mid=A[0];//选择枢轴
    while(L<R){
        while(A[R]>=mid && L<R) R--;
        A[L]=A[R];
        while(A[L]<=mid && L<R) L++;
        A[R]=A[L];
    }
    A[L]=mid;//划分位置的值
    return L;//返回划分的位置
}
int func(int A[],int n,int K){//找到第K小的元素
    int L=1,R=n,M=0;
    while(1){
        M = huafen(A,L,R);
        if(M==K) break;
        else if(M > K) R=M-1;
        else if(M < K) L=M+1;
    }
    return A[K];
}

最优解

int huafen (A[],int L,int R){
    int mid=A[0];//选择枢轴
    while(L<R){
        while(A[R]>=mid && L<R) R--;
        A[L]=A[R];
        while(A[L]<=mid && L<R) L++;
        A[R]=A[L];
    }
    A[L]=mid;//划分位置的值
    return L;//返回划分的位置
}
int func(int A[],int n){//找到第K小的元素
    int K=n/2;
    int L=0,R=n-1,M=0;
    while(1){
        M = huafen(A,L,R);
        if(M==K-1) break;
        else if(M > K-1) R=M-1;
        else if(M < K-1) L=M+1;
    }
    return A[K-1];
}

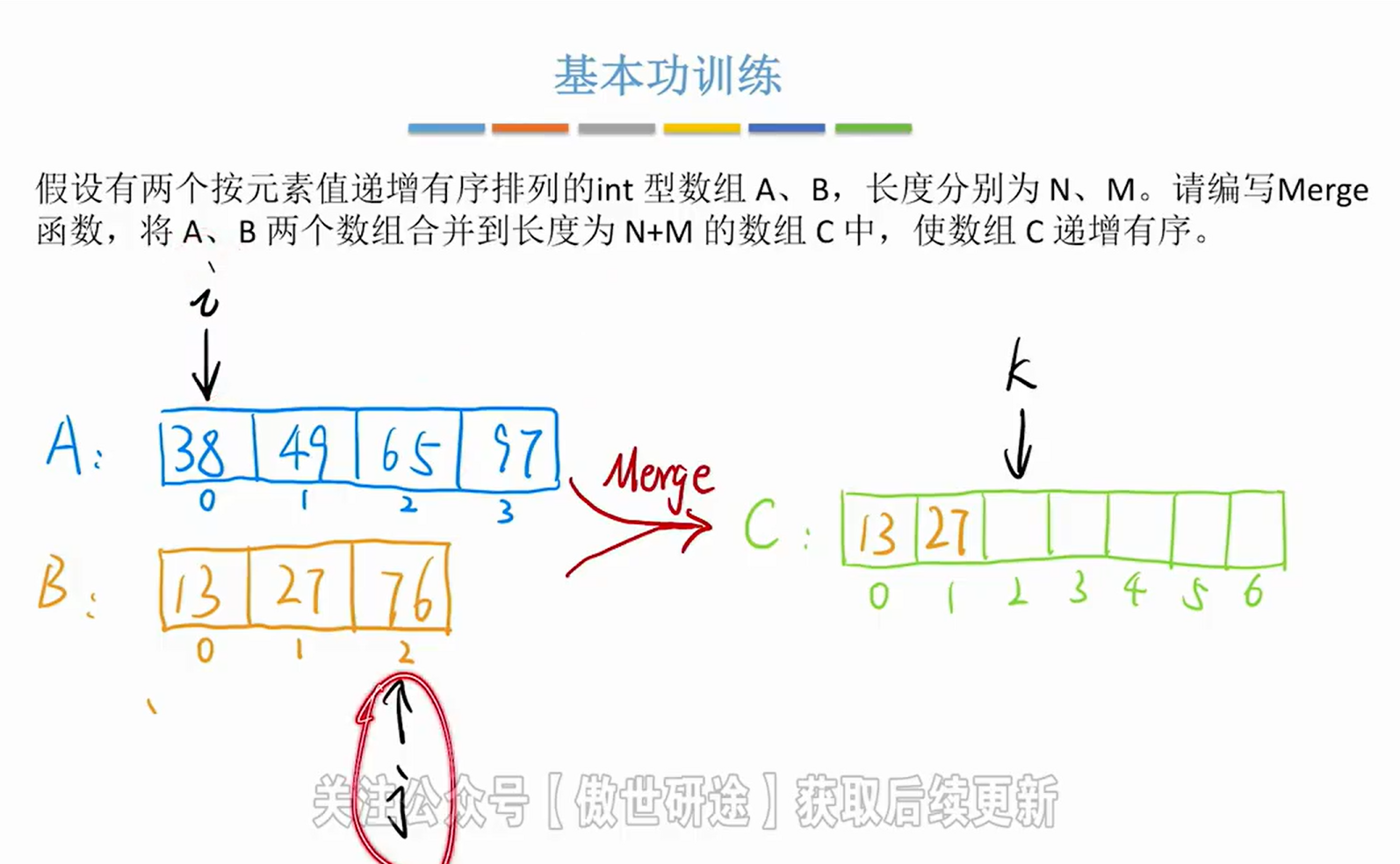
3.二路归并

int Merge(int A[],int n,int B[],int m,int C[]){
    int i=0,j=0,k=0;
    while(i<n && j<m){
        if(A[i]<=B[j]) C[k++]=A[i++];
        else C[k++]=B[j++];
    }
    while(i<n) C[k++]=A[i++];
    while(j<m) C[k++]=B[j++];
    return 1;
}

Merge 操作的空间复杂度为O(n)。

一趟Merge（归并）的时间复杂度为O(n)。

二路归并中，共需要log₂n趟，故时间复杂度为O(nlog₂n)

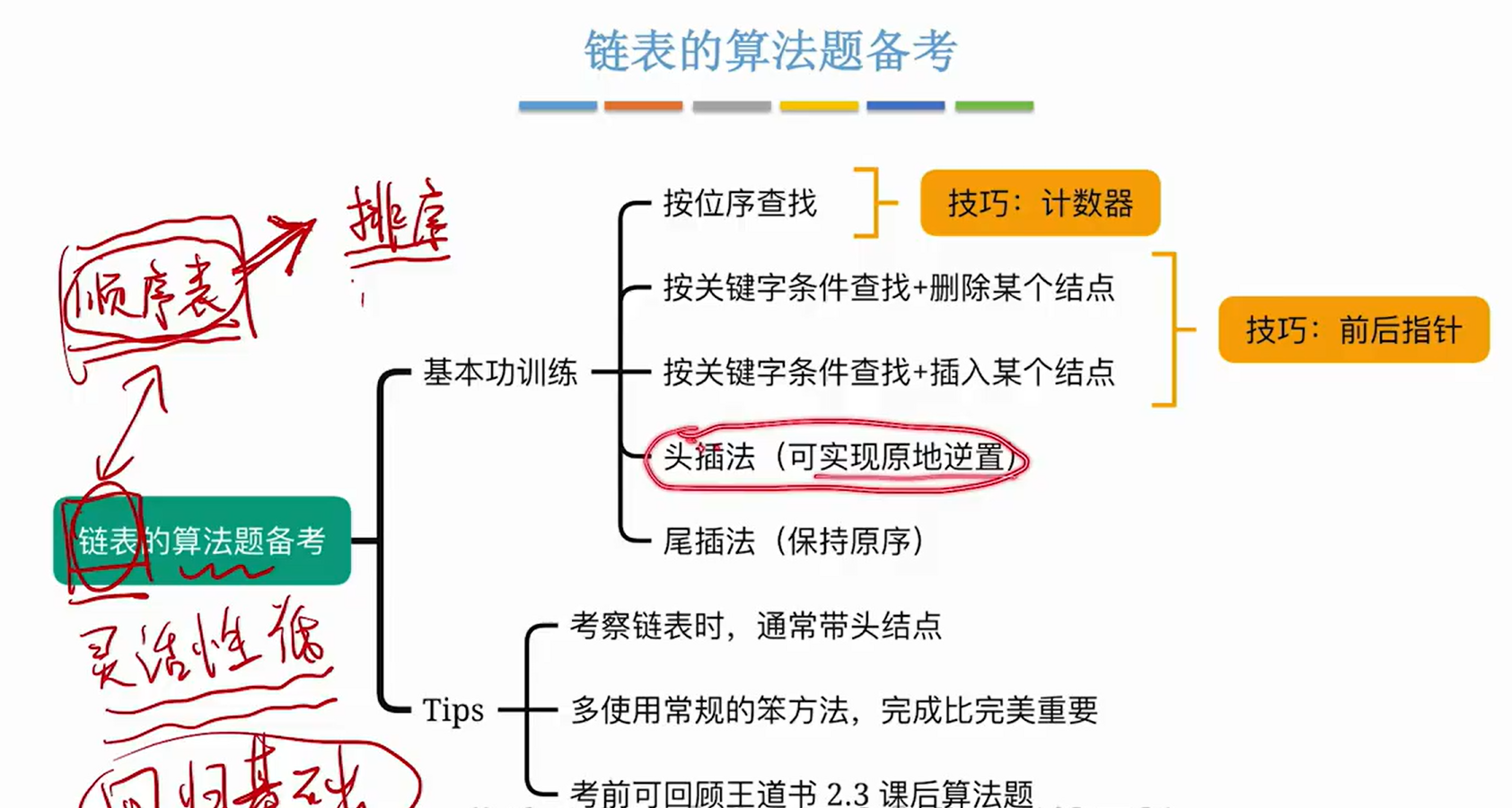
4.链表

1>使用计数器统计链表的长度

//定义单链表结点
typedef struct LNode{
    int data;
    struct 	LNode* next;
}LNode, *LinkList;
//求单链表长度
int listLen(LinkList L){
    int length=0;
    LNode *p=L->next;
    while (p!=NULL){
        length++;
        p=p->next;
    }
    printf("链表的长度 = %d \n",length);
    return length;
}
//返回单链表的中间结点
int findMidNode(LinkList L){
    int length=0;
    LNode *p=L->next;
    while (p!=NULL){
        length++;
        p=p->next;
    }
    int count=0;//计数器
    p= L->next;//让p指向头节点的下一个节点，（从头开始遍历）
    while(p!=NULL){
        if(count == lengtj/2) break;//找到中间结点，跳出循环
        p=p->next;//指向下一个结点
    }
    p=p->next;
    return p;
}

//求单链表长度
int listLen(LinkList L){
    int length=0;
    LNode *p=L->next;
    while (p!=NULL){
        length++;
        p=p->next;
    }
    return length;
}
//返回指针类型
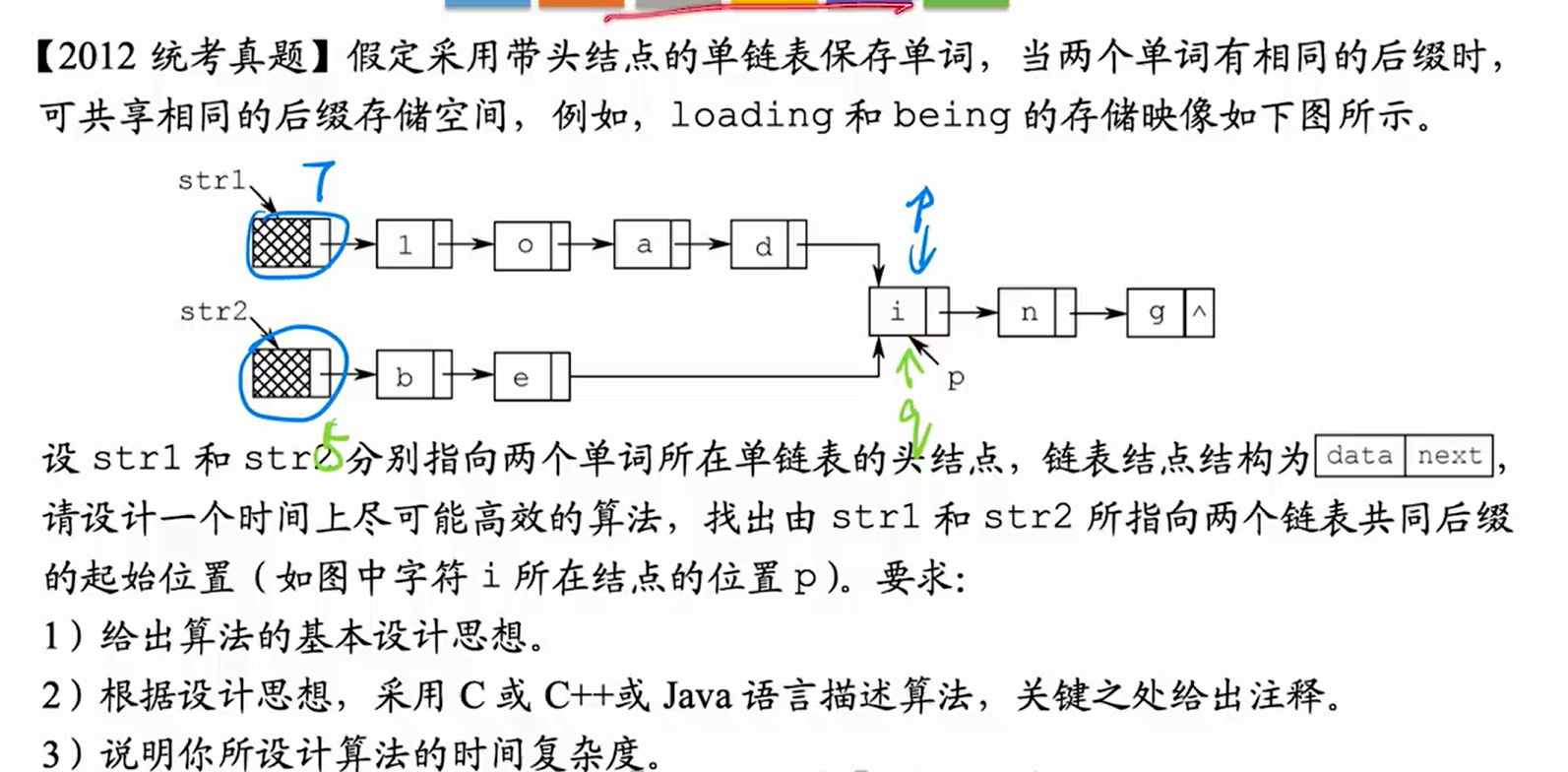
LinkNode *Find_1st_Common(LinkList str1,LinkList str2){
    int len1=listLen(str1),len2=listLen(str2);
    LinkNode *p,*q;
    for(p=str1;len1>len2;len1--) //使 p 指向的链表与 q 指向的链表等长
    	p=p->next;
    for(q=str2;len1<len2;len2--) //使 q 指向的链表与 p 指向的链表等长
   		q=q->next;
    while(p->next!=NULL&&p->next!=q->next){//查找共同后缀起始点
        p=p->next; //两个指针同步向后移动
        q=q->next;
    }
    return p->next; //返回共同后缀的起始点
}

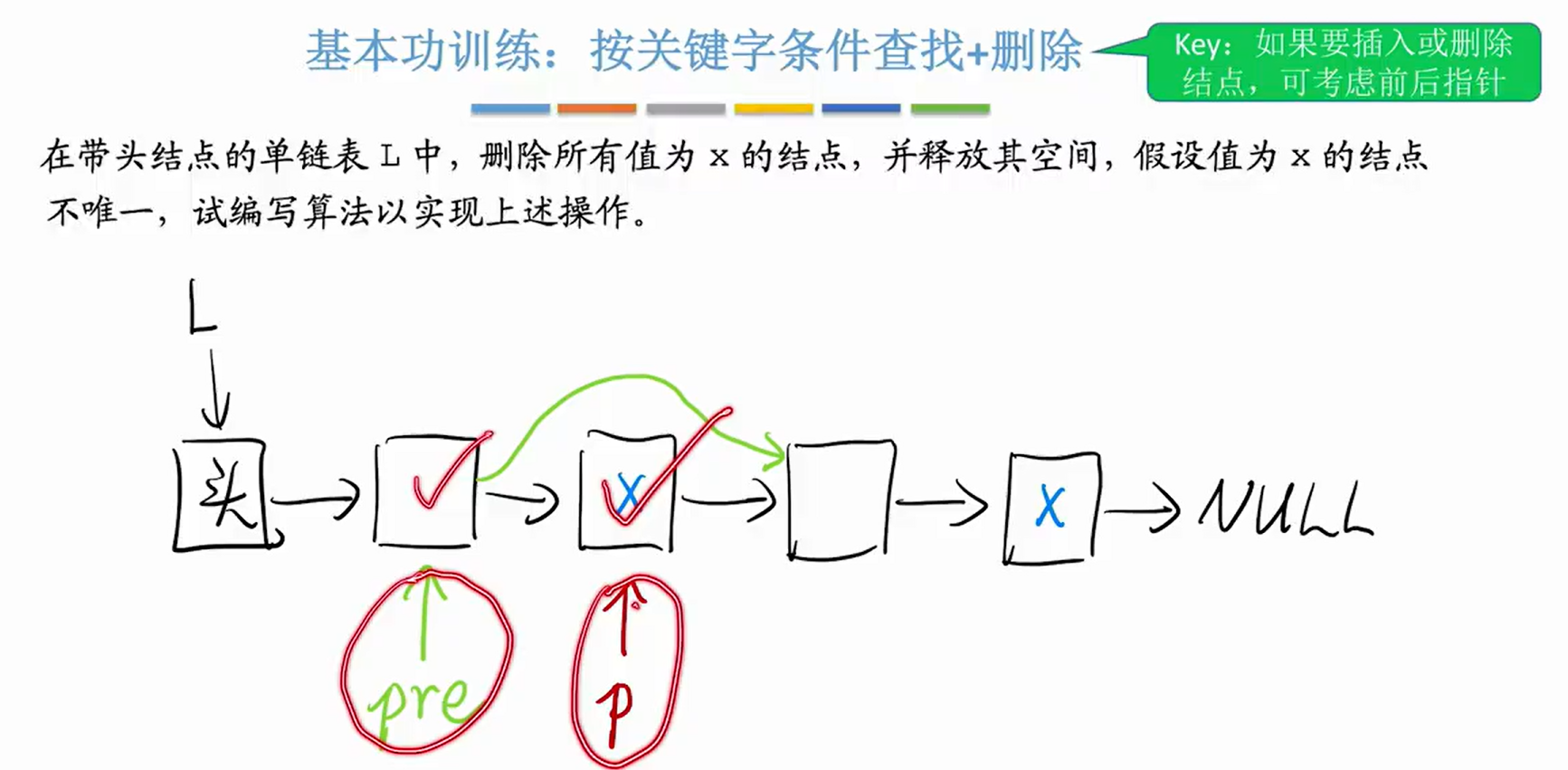
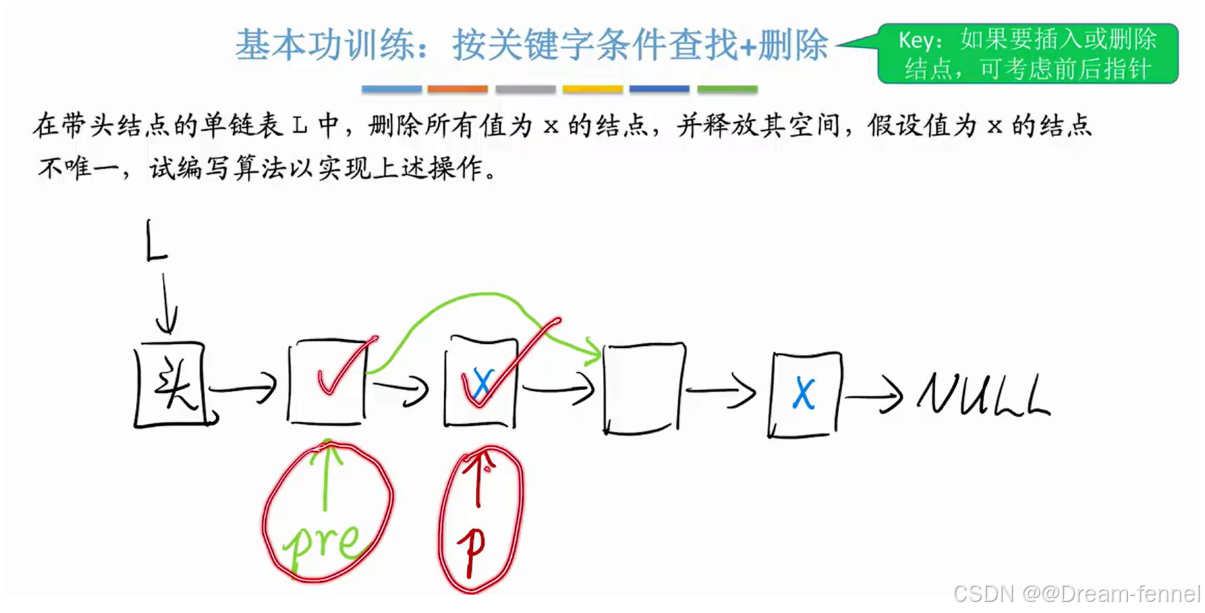
2>按照关键字条件查找+删除

//删除值为X的结点
int deletX(LinkList L,int x){
    LNode *pre = L;  //pre指向p的前驱节点
    LNode *p =pre ->next;//指向pre的下一个结点
    while(p!=NULL){
        if(p->data==x){
            LNode *q = p;//释放值为x的结点
            pre->next = p->next;//删除节点，修改指针
            free(q);
        }else{
            pre = p;//两个指针同时移动
            p= p->next;
        }
    }
}

3>按照关键字条件查找+插入

void InsertX(LinkList L,int x){
    LNode *pre = L;
    LNode *p = pre->next;
    while (p!=NULL){
        if(p->data >x){
            break;
        }else{
            pre = p;
            p = p->next;
        }
    }
    LNode *q= (LNode *)malloc(sizeof(LNOde));//等价与LinkList q = (LinkList)malloc(sizeof(*q));
    q->data = x;
    q->next=p;
    pre->next = q;
}

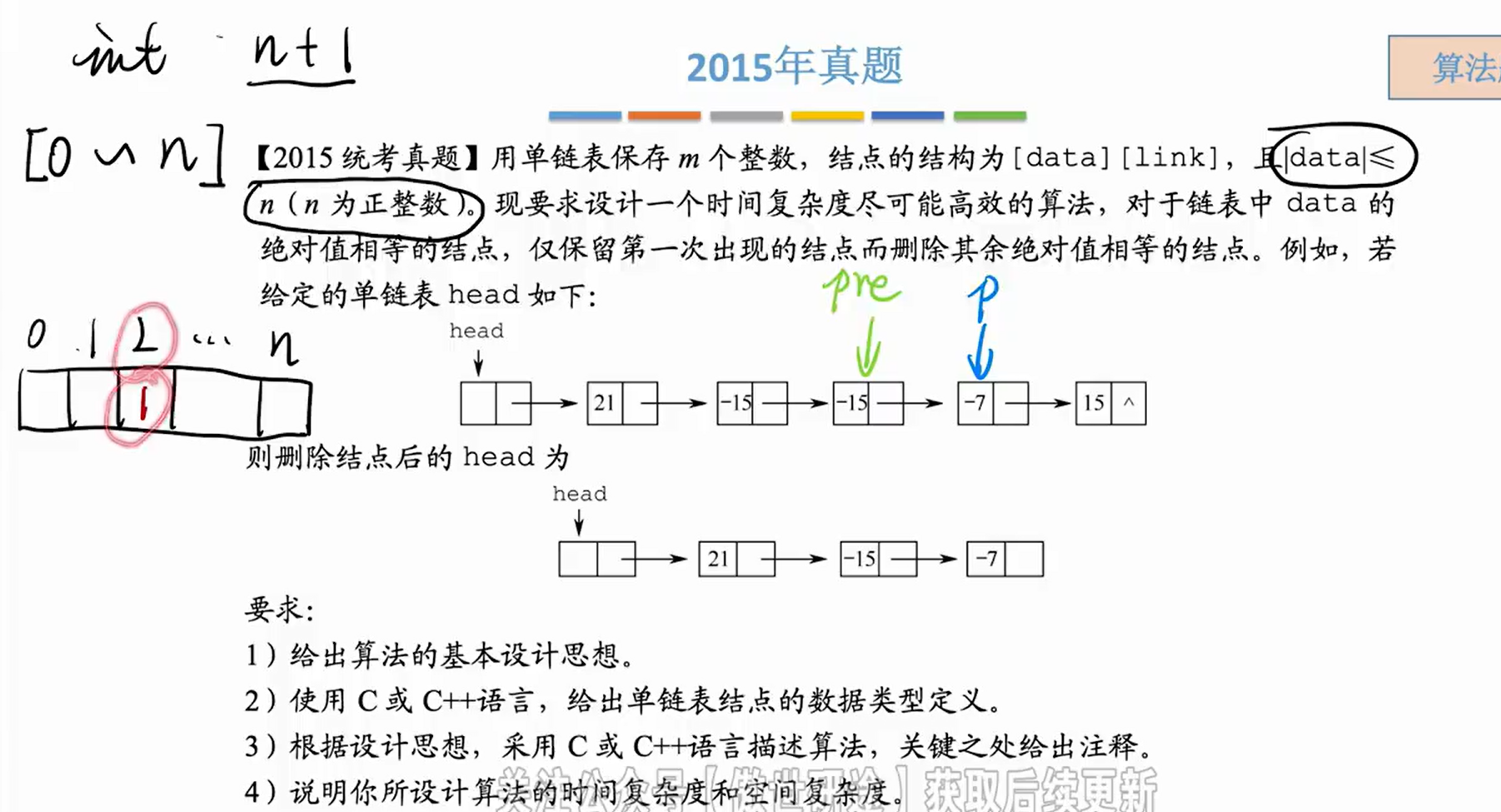
typedef struct LNode{
    int data;
    struct LNode* next;
}LNode,*LinkList;

// 函数功能：删除链表中绝对值重复出现的节点，只保留第一次出现的节点
void Del(LinkList L,int n){
    // 遍历链表，将负数节点的值取绝对值
    LNode *p = L;
    while (p!=NULL){
        if(p->data <0){
            p->data = -p->data; 
        }
        p = p->next;
    }
    // 创建辅助数组，用于标记已出现的绝对值
    int a[n + 1] = {0};

    // prev 用于指向当前节点的前一个节点
    LNode *prev = NULL;
    // 重新将 p 指向链表头节点，开始处理链表
    p = L;
    while (p!=NULL){
        // 获取当前节点值的绝对值
        int Data = p->data;
        if (a[Data] == 0) {
            // 如果该绝对值第一次出现
            // 将辅助数组中对应位置标记为已出现
            a[Data] = 1;
            // prev 指向当前节点
            prev = p;
            // p 指向下一个节点，继续遍历
            p = p->next;
        } else {
            // 如果该绝对值不是第一次出现
            // 将当前节点存储在 toDelete 中，准备删除
            LNode *toDelete = p;
            // p 指向下一个节点，继续遍历
            p = p->next;
            if (prev!= NULL) {
                // 如果当前节点不是头节点，将 prev 的 next 指针指向当前节点的下一个节点
                prev->next = p;
            } else {
                // 如果当前节点是头节点，更新头指针
                L = p;
            }
            // 释放要删除的节点的内存空间
            free(toDelete);
        }
    }
}

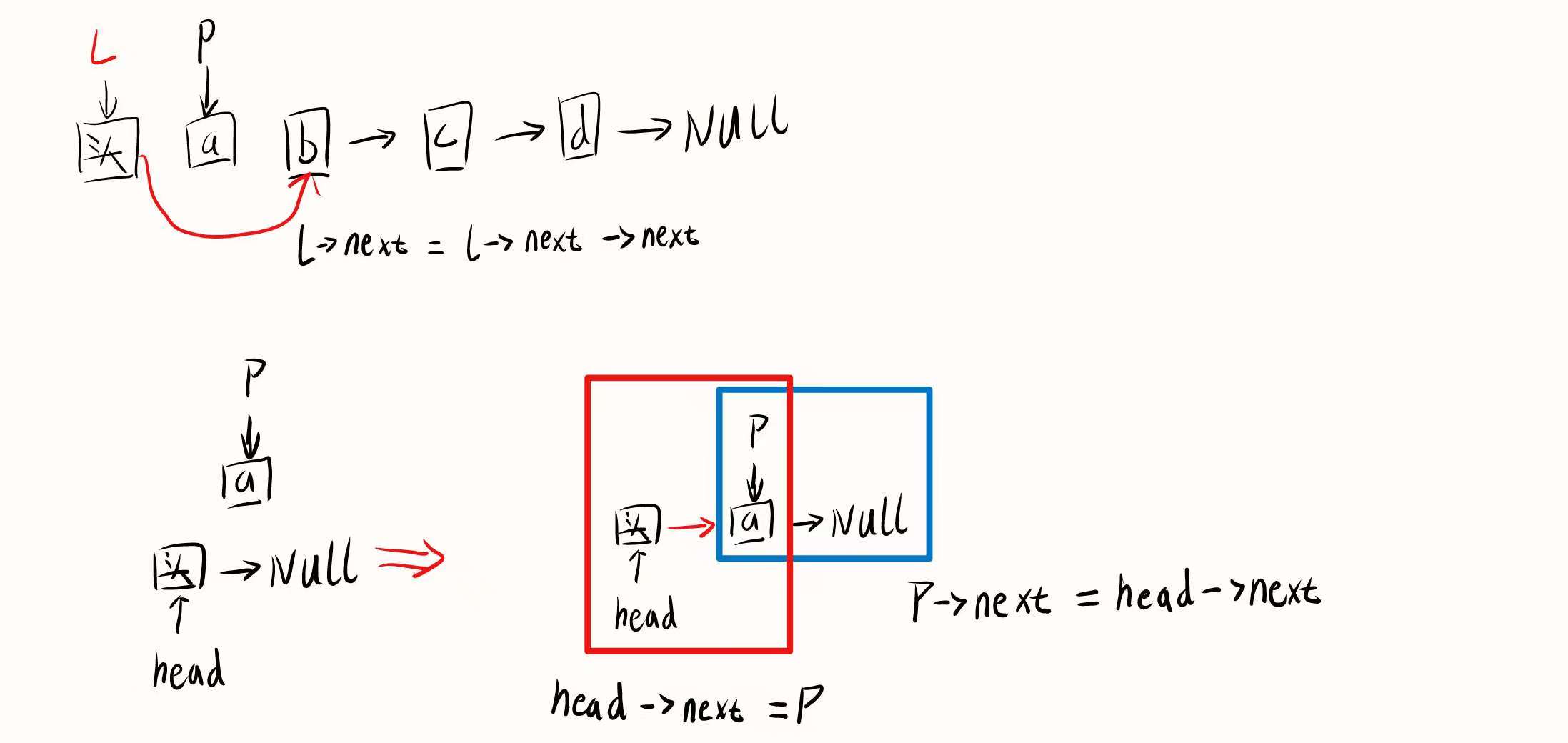
5.头插法（原地逆置）

void ListReserve(LinkList L){
    //分配一个辅助头结点
    LinkList head = (LNOde *) malloc (sizeof(LNOde));
    head->next = NULL;
    while (L->next != NULL){
        LNode *p = L->next; //按顺序拆下每个结点
        L->next = L->next->next;
        
        p->next = head->next;//头插法
        head->next = p;//将头结点链接到第一个元素
    }
    L->next = head->next;//将逆置好的链表链接回原链表
    free(head);//释放辅助头结点
}

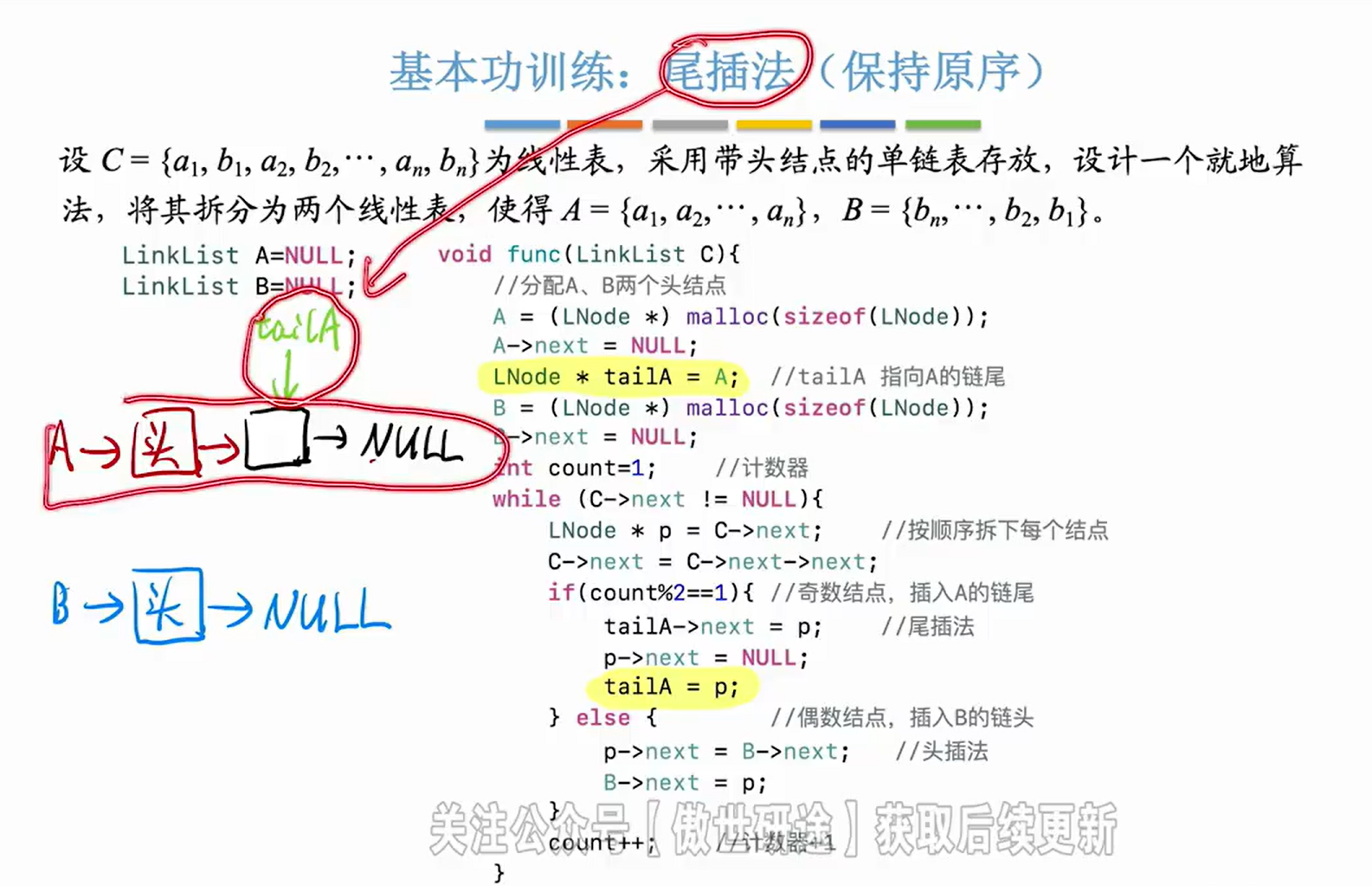
6.尾插法（保持原序）

LinkList A;//用于尾插法
LinkList B;//用于头插法
void func(LinkList C){
    //分配A、B两个头结点
    A = (LNode *) malloc(sizeof(LNode));
    A->next = NULL;
    LNode *tailA = A;//tailA 一直指向A的链尾
    B = (LNode *)malloc(sizeof(LNode));
    B->next = NULL;
    int count =1;
    while(C-next != NULL){
        LNode *p =C-next;//按照顺序拆下每个结点；指向C的第一个元素
        C->next = C->next->next;
        if(count %2==1){
            //原序
            tailA->next = p;//将新的结点链接到尾结点
            p->next = NULL;//将尾结点执指向NULL
            tailA = p;//尾指针移动到新的尾结点
        }else{
            //逆序
            p->next = B->next;//头插法
            B->next = p;
        }
        count++;
    }
}

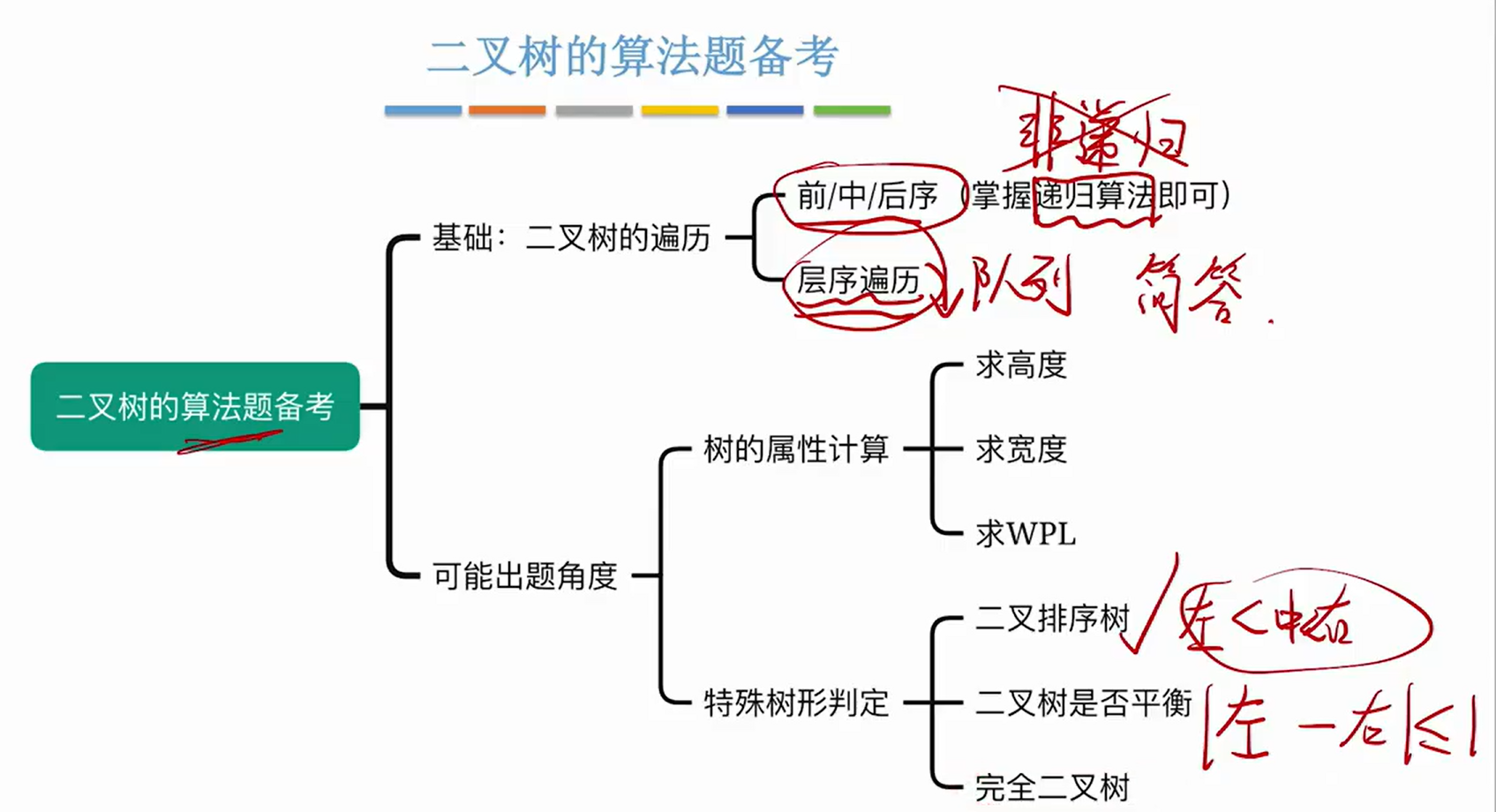
7.二叉树

1>前/中/后序遍历

//二叉树的结点定义（链式存储）
typedef struct BiTNode {
    int data;
    struct BiTNode *lchild,*rchild;
}BiTNode,*BiTree;
//此处可写对根节点的操作
void visit(BiTree T, int level) {
    if (T!= NULL) {
        printf("节点 %d 在第 %d 层\n", T->data, level);
    }
}


// 计算平衡因子的辅助函数
int getBalanceFactor(BiTree T) {
    if (T == NULL) {
        return 0;
    }
    int leftHeight = treeHeight(T->lchild);
    int rightHeight = treeHeight(T->rchild);
    return leftHeight - rightHeight;
}
// 前序遍历
void preOrder(BiTree T,int level) {
    if (T == NULL) {
        return;
    }
    int BalanceFactor= getBalanceFactor(T);
    visit(T, level);//访问根节点,结点所在层数
    printf("输出平衡子：%d",BalanceFactor);
    if(BalanceFactor >1 or BalanceFactor <-1) return 1
    preOrder(T->lchild,level + 1);//遍历左子树
    preOrder(T->rchild,level + 1);//遍历右子树
}

// 中序遍历
void inOrder(BiTree T,int level) {
    if (T == NULL) {
        return;
    }
    inOrder(T->lchild,level + 1);
    visit(T, level);
    inOrder(T->rchild,level + 1);
}

// 后序遍历
void postOrder(BiTree T,int level) {
    if (T == NULL) {
        return;
    }
    postOrder(T->lchild,level + 1);//左
    postOrder(T->rchild,level + 1);//右
    visit(T, level);
}

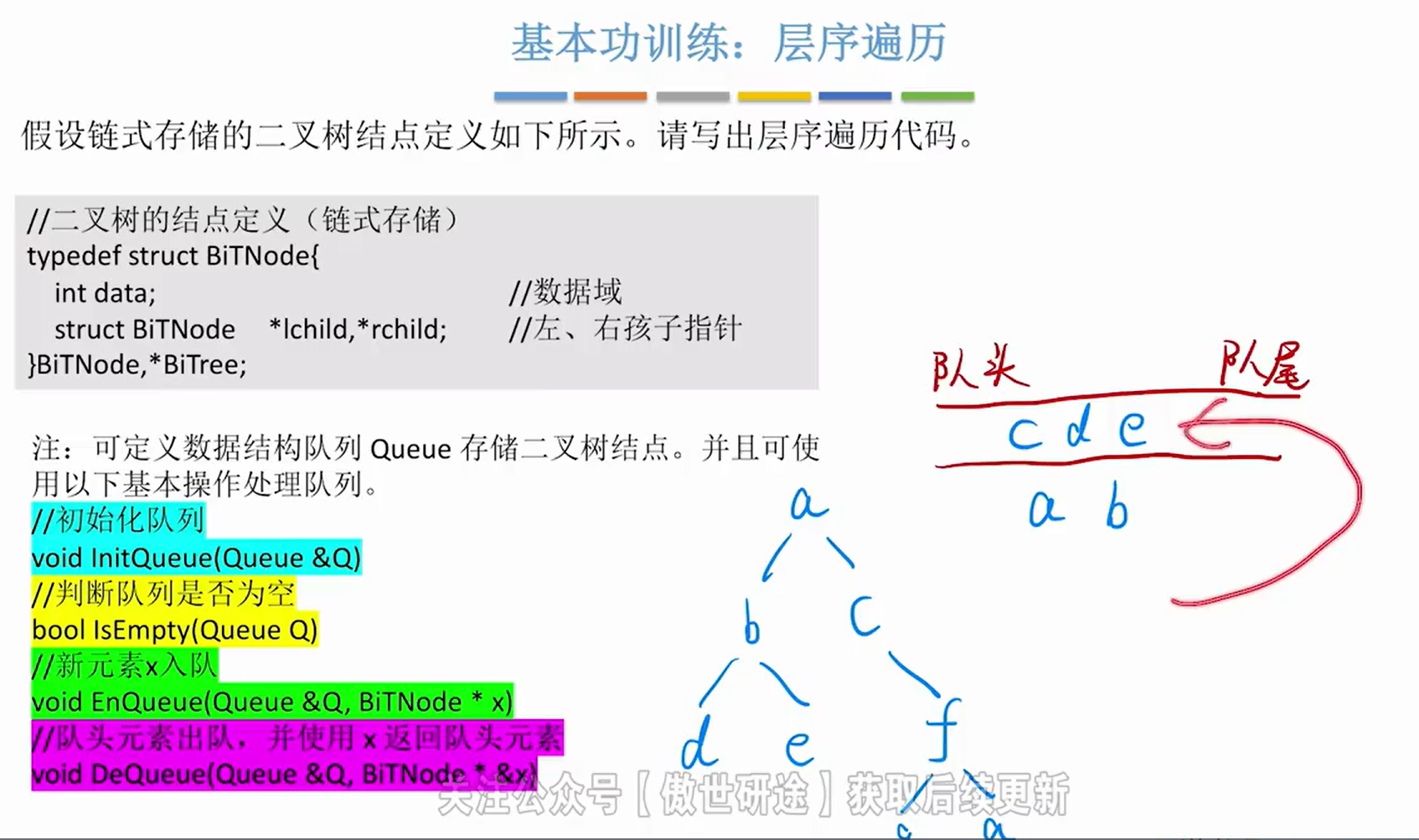
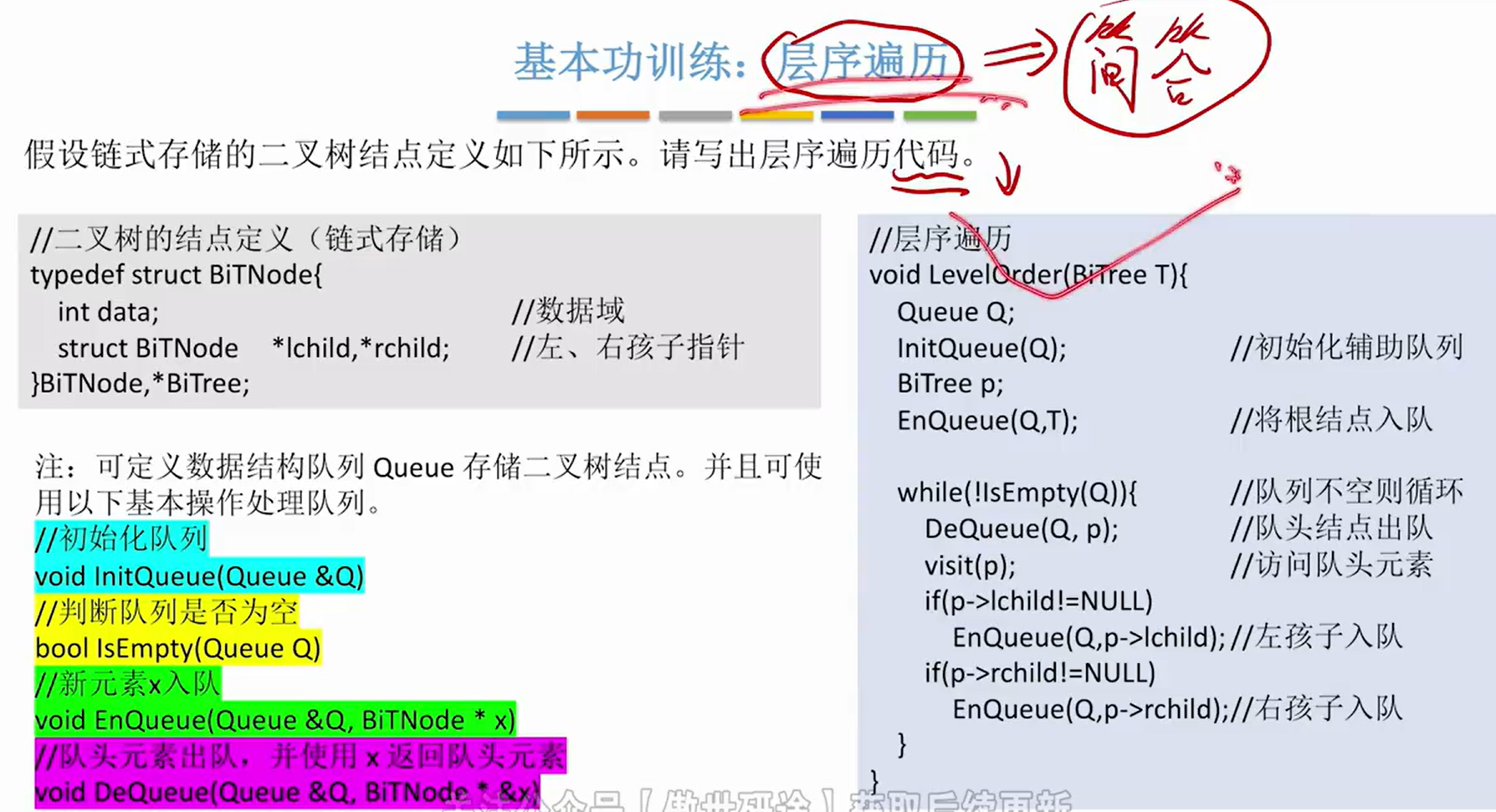
2>层序遍历

注意：更容易靠简答题；如果考算法题直接使用辅助队列即可

//二叉树的结点定义（链式存储）
typedef struct BiTNode{
    int data;//数据域
    struct BiTNode *lchild,*rchild;//左、右孩子指针
}BiTNode,*BiTree;

//层序遍历
void LevelOrder(BiTree T){
    Queue Q;
    InitQueue(Q);//辅助函数（初始化辅助队列）
    BiTree p;
    EnQueue(Q,T);//辅助函数，将根结点入队
    while (!IsEmpty(Q)){   //队列不为空循环
        DeQueue(Q,p);		//对头结点出队（辅助函数）
        visit(p);			//访问队头元素（辅助函数）
        if(p->lchild != NULL){
            EnQueue(Q,p->lchild);//左孩子入队
        }
        if(p->rchild != NULL){
            EnQueue(Q,p->rchild);//右孩子入队
        }
    }
}

3>求树的高度

//二叉树的结点定义（链式存储）
typedef struct BiTNode {
    int data;
    struct BiTNode *lchild,*rchild;
}BiTNode,*BiTree;
// 求二叉树的高度
//方法一（先序遍历的改版）
int height =0;
void PreOrder (BiTree,int n){
    if(T==NULL) return;
    if(n>height) height=n;//更新树的高度
    PreOrder(T->lchild,n+1);//遍历左子树
    PreOrder(T->rchild,n+1);//遍历右子树
}
//方法二
int treeHeight(BiTree T) {
    if (T == NULL) {
        return 0;
    }
    int leftHeight = treeHeight(T->lchild);
    int rightHeight = treeHeight(T->rchild);
    return (leftHeight > rightHeight? leftHeight : rightHeight) + 1;//找到最大的然后加1；（加1是，加上根节点）
}

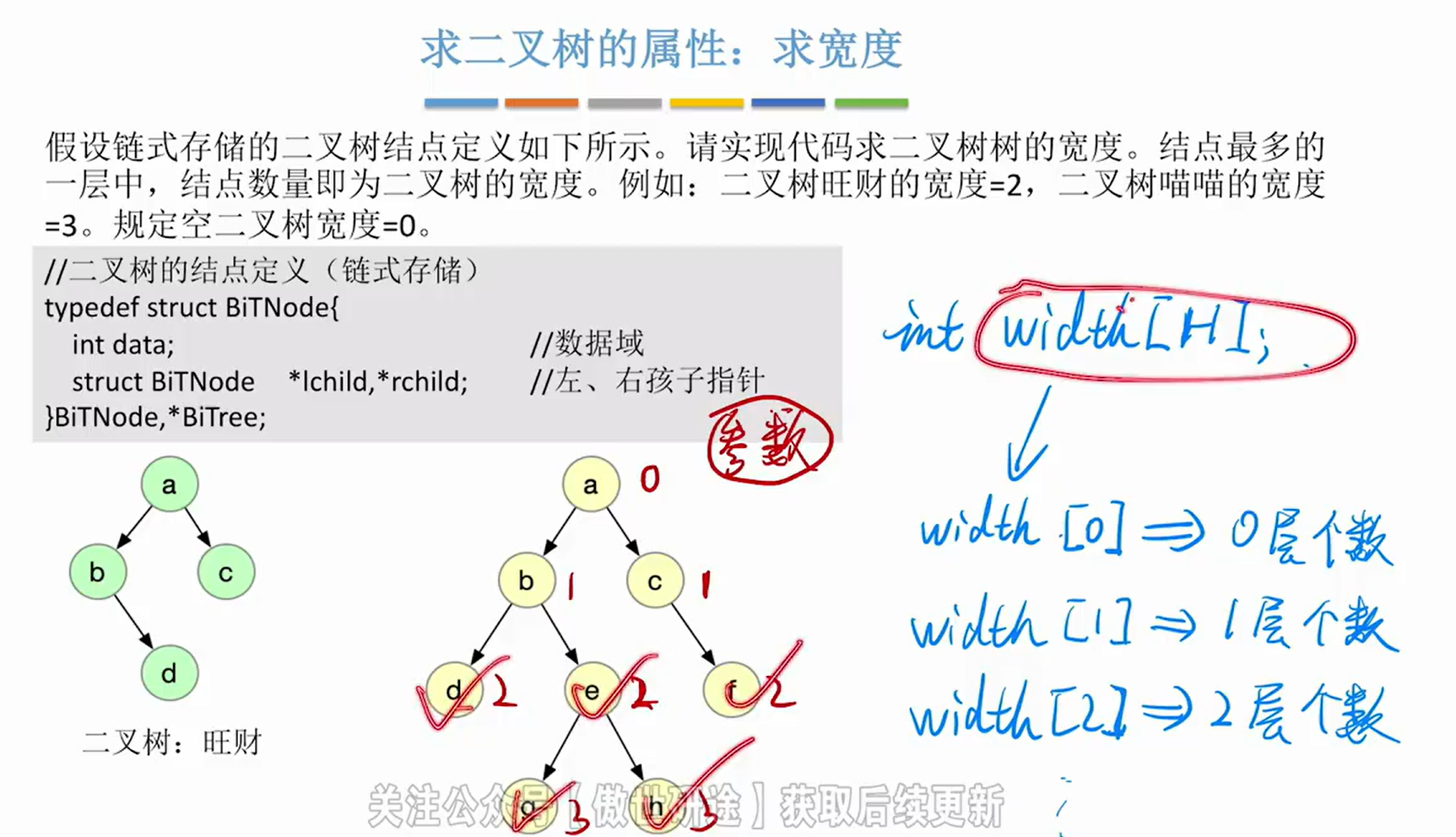
4>求树的宽度

//二叉树的结点定义（链式存储）
typedef struct BiTNode {
    int data;
    struct BiTNode *lchild,*rchild;
}BiTNode,*BiTree;
//使用先序遍历统计，同时各层结点总数
int width[MAX];//用于统计各层结点总数
void ProOrder(BiTree T,int level){
    if(T==NULL) return;
    width[level]++;//累加该层节点总数
    ProOrder(T->lchild,level+1);//遍历左子树
    ProOrder(T->rchild,level+1)//遍历右子树
}
//求树的宽度
void treeWidth(BiTree T){
    for(int i=0;i<MAX;i++)
        width[i]=0;
    ProOrder(T,0);//先序遍历二叉树，统计各层结点总数
    int maxWidth = 0;//最大宽度
    for(int i=0;i<MAX;i++){
        if(width[i] > maxWidth)
            maxWidth = width[i];
    }
    printf("树的宽度是%d",maxwidth);
}

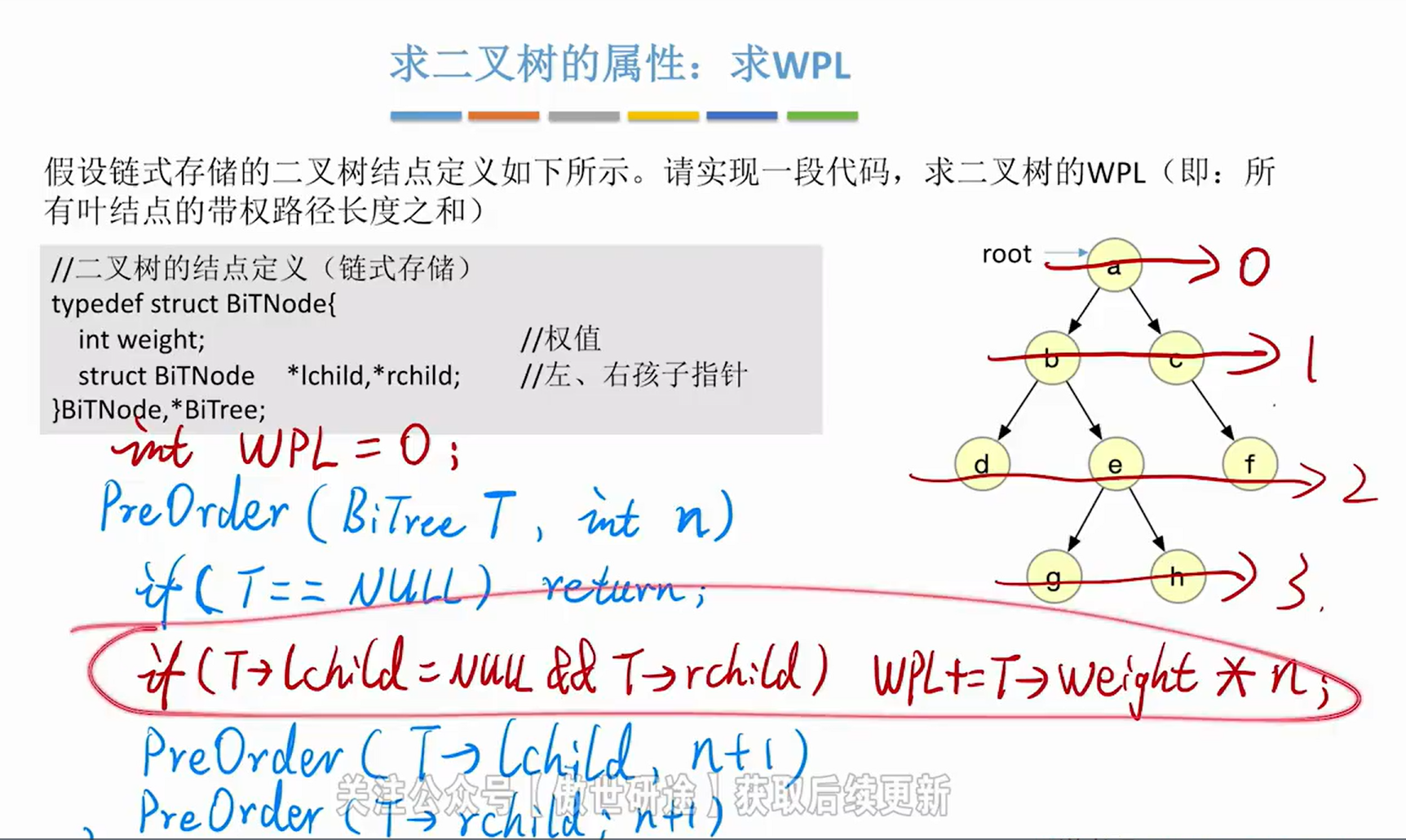
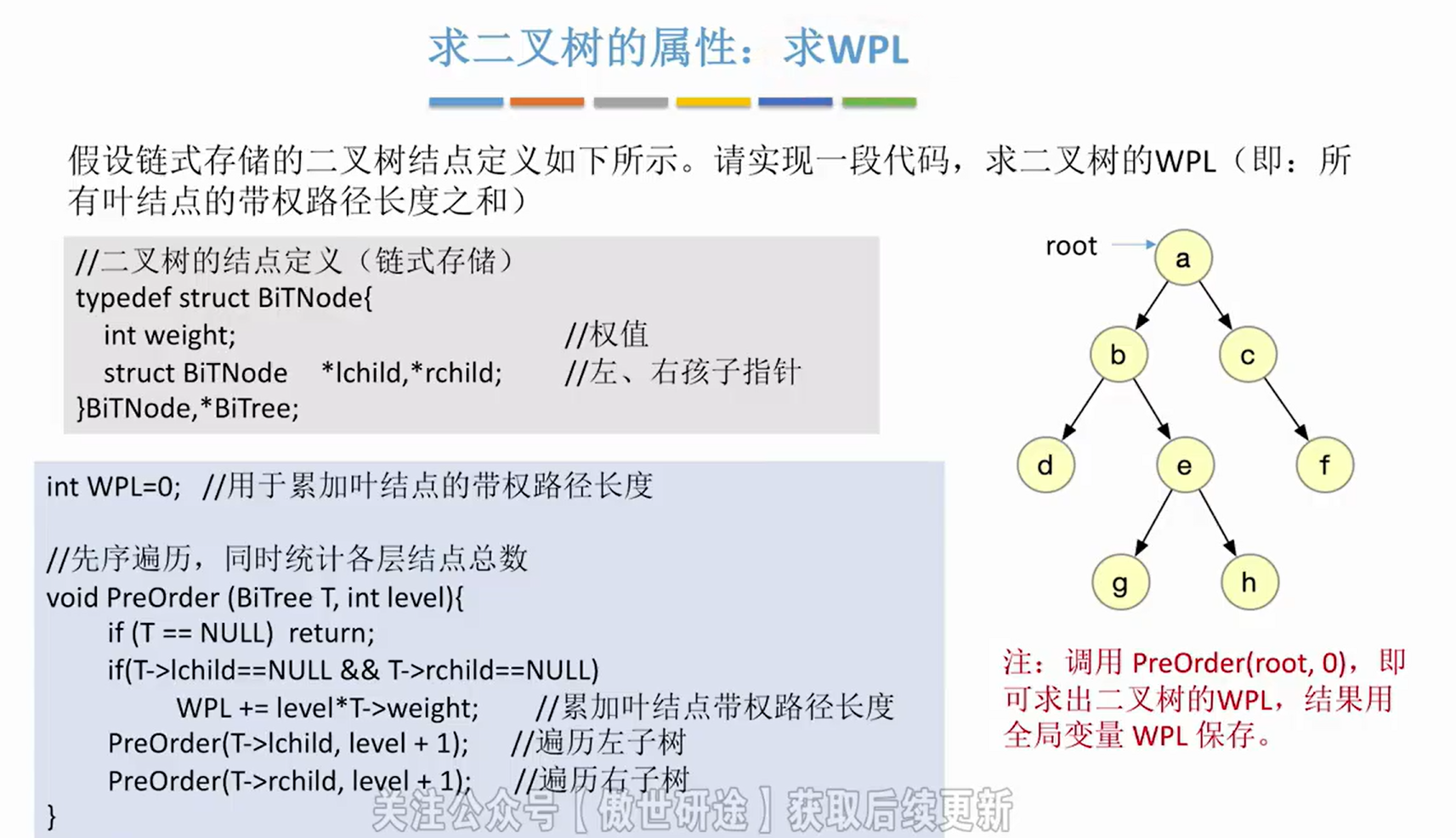
5->求WPL（带权路径长度）

//二叉树的结点定义（链式存储）
typedef struct BiTNode {
    int weight;
    struct BiTNode *lchild,*rchild;
}BiTNode,*BiTree;
int WPL=0;
//先序遍历
void PreOrder(BiTree T,int level){
    if(T == NULL) return;
    //处理，如果是叶子节点，叶子节点的权值乘以层数
    if(T->lchild == NULL&&T->rchild == NULL){
        WPL += level*T->weight; //累加叶结点带权路径长度
    }
    PreOrder(T->lchild,level + 1);//遍历左子树
    PreOrder(T->rchild,level + 1);//遍历右子树
}

6->判定二叉排序树

//二叉树的结点定义（链式存储）
typedef struct BiTNode {
    int weight;
    struct BiTNode *lchild,*rchild;
}BiTNode,*BiTree;

int temp = MIN_INT;
bool isBST=true;
void InOrder(BiTree T){
    if(T == NULL) return;
    InOrder(T-lchild);
    if(T->data >= temp) temp = T->data;
    else isBST = false;
    InOrder(T->rchild);
}

7->判定二叉树是否平衡

//二叉树的结点定义（链式存储）
typedef struct BiTNode {
    int weight;
    struct BiTNode *lchild,*rchild;
}BiTNode,*BiTree;

bool isBalance = true;
int PostOrder(BiTree T){
    if(T == NULL) return 0;
    int left = PostOrder(T->lchild);
    int right = PostOrder(T->rchild);
    
    if(left-right > 1) isBalance = false;
    if(left-right < -1) isBalance = false;
    //树的深度=MAX(左子树深度-右子树深度) + 1
    if(left > right) return left +1;
    else return right +1;
}

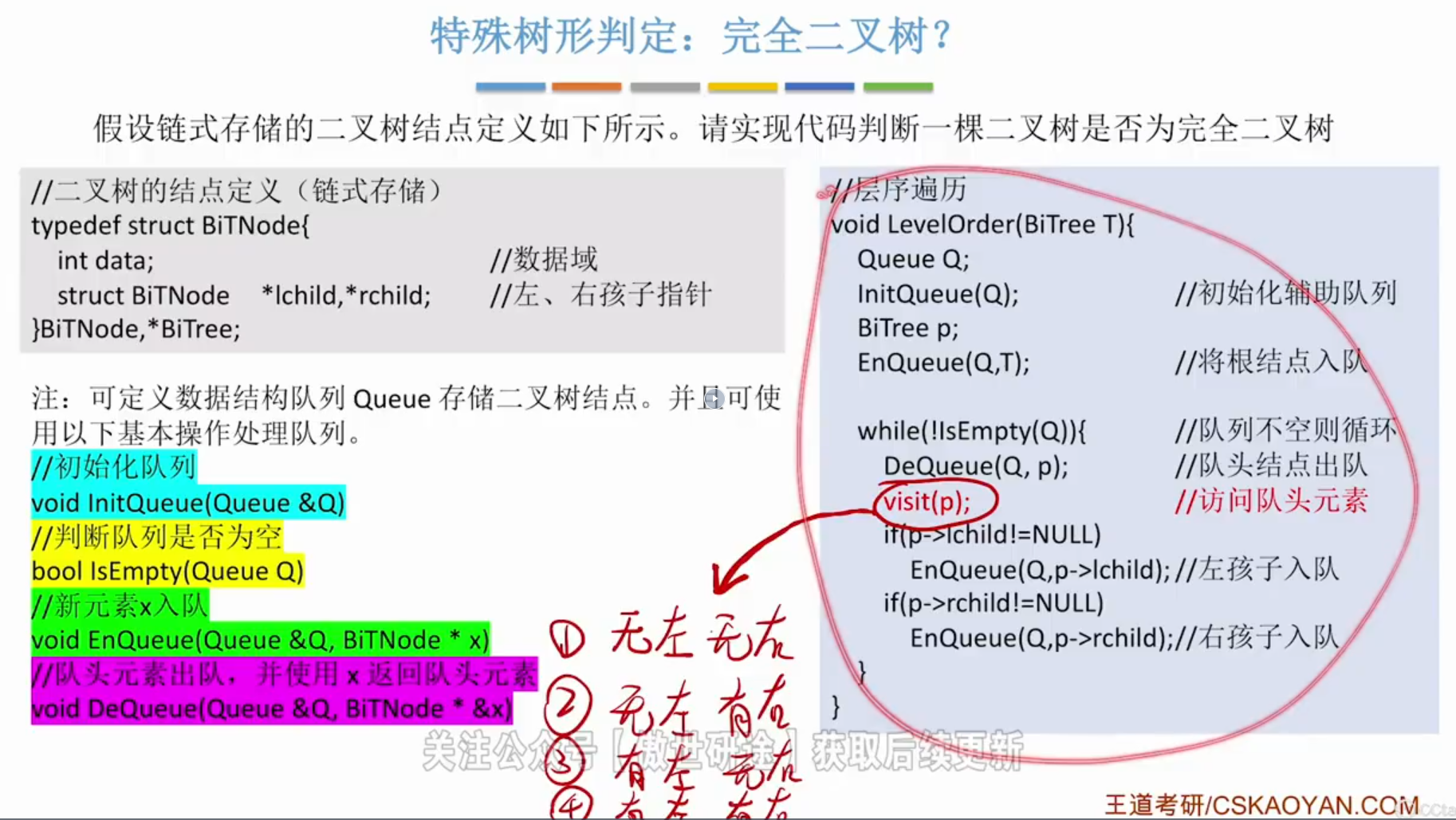
8->判定完全二叉树

想象层序遍历的过程：出队一个元素，入队该元素的所有孩子结点。

注：在完全二叉树中，一旦出现了叶子节点或者只有左孩子的分支节点，那么后续的节点必须都是叶子节点，不能再有有孩子的节点。

//二叉树的结点定义（链式存储）
typedef struct BiTNode{
    int data;//数据域
    struct BiTNode *lchild,*rchild;//左、右孩子指针
}BiTNode,*BiTree;

//层序遍历
void LevelOrder(BiTree T){
    Queue Q;
    InitQueue(Q);//辅助函数（初始化辅助队列）
    BiTree p;
    EnQueue(Q,T);//辅助函数，将根结点入队
    while (!IsEmpty(Q)){   //队列不为空循环
        DeQueue(Q,p);		//对头结点出队（辅助函数）
        visit(p);			//访问队头元素（辅助函数）
        if(p->lchild != NULL){
            EnQueue(Q,p->lchild);//左孩子入队
        }
        if(p->rchild != NULL){
            EnQueue(Q,p->rchild);//右孩子入队
        }
    }
}

bool isComplete = true; //是否为完全二叉树
bool flag = false;  //flag = true,表示层序遍历时出现过叶子或只有做孩子的分支节点

void visit(BiTNode *p){
    //既没有左孩子也没有右孩子，还不能判断不是完全二叉树
    if(p->lchild == Null && p->rchild ==NULL)  flag = true;
    if(p->lchild == Null && p->rchild !=NULL)  isComplete = false;//只有右孩子没有左孩子，直接判定不是完全二叉树
    if(p->lchild != NULL && p->child == NULL){  //有左无右
        if(flag) isComplete = false;  //如果flag=true说明之前出现了叶子节点，此时可直接判定不是完全二叉树
     	flag = true;  //否则此结点可能为完全二叉树
    }
    if(p->lchild != NULL && p->rchild != NULL){  //有左有右
        if(flag)  isComplete = false;  //如果flag=true说明之前出现了叶子节点，此时可直接判定不是完全二叉树
    }
}