🌈hello,你好鸭,我是Ethan,西安电子科技大学大三在读,很高兴你能来阅读。
✔️目前博客主要更新Java系列、项目案例、计算机必学四件套等。
🏃人生之义,在于追求,不在成败,勤通大道。加油呀!
🔥个人主页:Ethan Yankang
🔥推荐:史上最强八股文 || 一分钟看完我的上千篇博客
🔥温馨提示:划到文末发现专栏彩蛋 点击这里直接传送
🔥本篇概览:数据结构与算法 || 详细讲解了回溯算法在分割字符串方面的运用。🌈⭕🔥
【计算机领域一切迷惑的源头都是基本概念的模糊,算法除外】
🌈序言
算法乃我长久之志也,此关必过。今日得此代码随想录之良品辅助,应按此路学之习之,而长久不可懈怠。
前一系列文章详细讲解了回溯算法在组合问题中的使用,建议先将这部分知识掌握之后再来学习本篇内容,点击查看。
🔥 代码随想录95——回溯算法6——组合5——组合总和II-CSDN博客
🌈引出
切割问题其实是一种组合问题!
题目:131.分割回文串
给定一个字符串 s,将 s 分割成一些子串,使每个子串都是回文串。
返回 s 所有可能的分割方案。
示例: 输入: "aab" 输出: [ ["aa","b"], ["a","a","b"] ]
剖析题干重点:
1.如何分割子串
2.判断回文
🔥思路分析:
本题这涉及到两个关键问题:
- 切割问题,有不同的切割方式
- 判断回文
相信这里不同的切割方式可以搞懵很多同学了。
这种题目,想用for循环暴力解法,可能都不那么容易写出来,所以要换一种暴力的方式,就是回溯。
一些同学可能想不清楚 回溯究竟是如何切割字符串呢?
我们来分析一下切割,其实切割问题类似组合问题。
例如对于字符串abcdef:
- 组合问题:选取一个a之后,在bcdef中再去选取第二个,选取b之后在cdef中再选取第三个.....。
- 切割问题:切割一个a之后,在bcdef中再去切割第二段,切割b之后在cdef中再切割第三段.....。
感受出来了不?
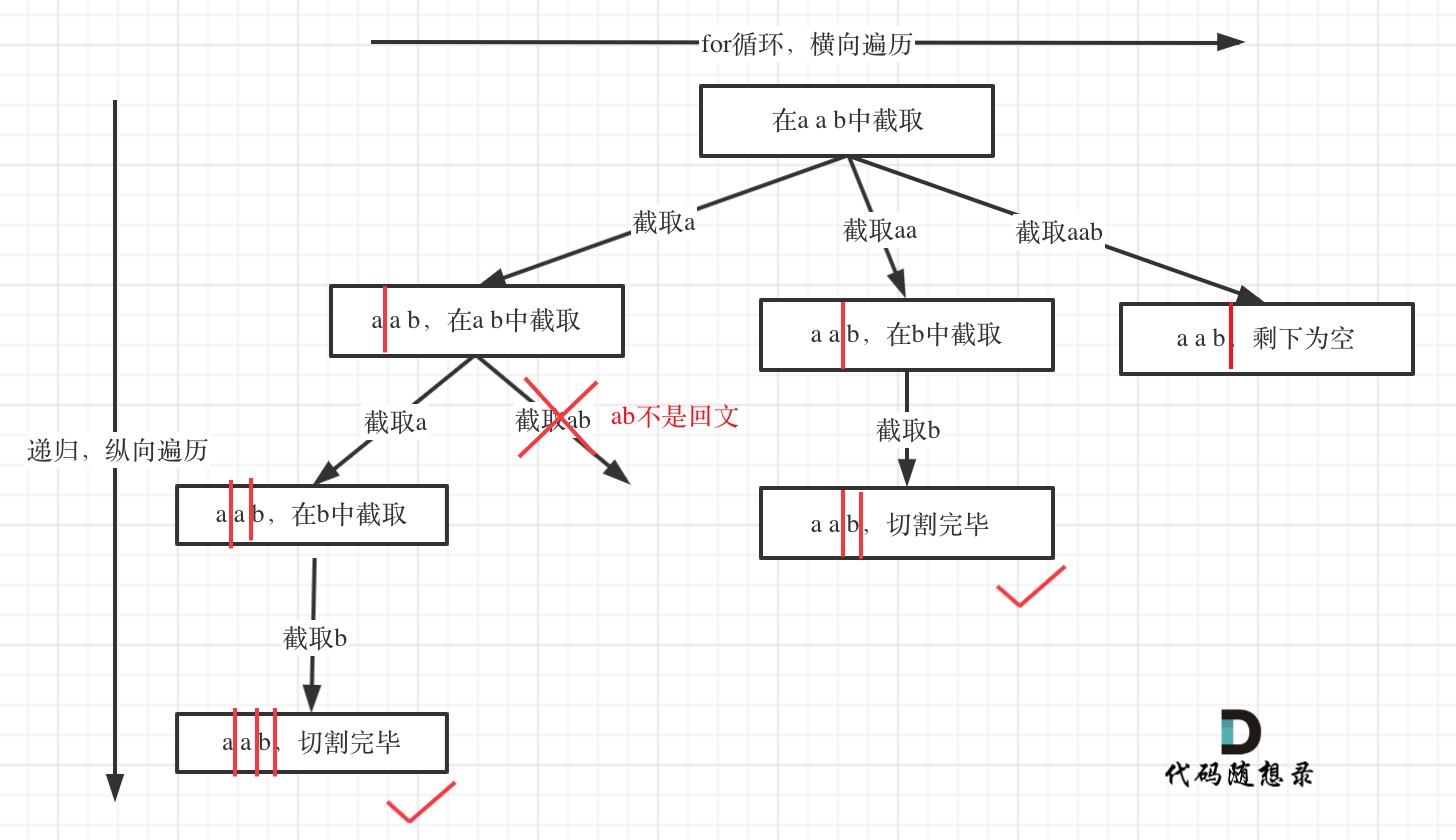
所以切割问题,也可以抽象为一棵树形结构,如图:
递归用来纵向遍历,for循环用来横向遍历,切割线(就是图中的红线)切割到字符串的结尾位置,说明找到了一个切割方法。
此时可以发现,切割问题的回溯搜索的过程和组合问题的回溯搜索的过程思想是一致的。
回溯三部曲
-
递归函数参数
全局变量数组path存放切割后回文的子串,二维数组result存放结果集。 (这两个参数可以放到函数参数里)
本题递归函数参数还需要startIndex,因为切割过的地方,不能重复切割,和组合问题也是保持一致的。
在回溯算法:求组合总和(二) (opens new window)中我们深入探讨了组合问题什么时候需要startIndex,什么时候不需要startIndex。—————
本题还需要startIndex来控制for循环的起始位置,对于组合问题,什么时候需要startIndex呢?
我举过例子,如果是一个集合来求组合的话,就需要startIndex,例如:77.组合 (opens new window),216.组合总和III (opens new window)。
如果是多个集合取组合,各个集合之间相互不影响,那么就不用startIndex,例如:17.电话号码的字母组合(opens new window)
注意以上我只是说求组合的情况,如果是排列问题,又是另一套分析的套路,后面我在讲解排列的时候会重点介绍。
代码如下:
vector<vector<string>> result;
vector<string> path; // 放已经回文的子串
void backtracking (const string& s, int startIndex) {
-
递归函数终止条件
从树形结构的图中可以看出:切割线切到了字符串最后面,说明找到了一种切割方法,此时就是本层递归的终止条件。
那么在代码里什么是切割线呢?
在处理组合问题的时候,递归参数需要传入startIndex,表示下一轮递归遍历的起始位置,这个startIndex就是切割线。
所以终止条件代码如下:
void backtracking (const string& s, int startIndex) {
// 如果起始位置已经大于s的大小,说明已经找到了一组分割方案了
if (startIndex >= s.size()) {
result.push_back(path);
return;
}
}-
单层搜索的逻辑
来看看在递归循环中如何截取子串呢?
在for (int i = startIndex; i < s.size(); i++)循环中,我们 定义了起始位置startIndex,那么 [startIndex, i] 就是要截取的子串。
首先判断这个子串是不是回文,如果是回文,就加入在vector<string> path中,path用来记录切割过的回文子串。
代码如下:
for (int i = startIndex; i < s.size(); i++) {
if (isPalindrome(s, startIndex, i)) { // 是回文子串
// 获取[startIndex,i]在s中的子串
string str = s.substr(startIndex, i - startIndex + 1);
path.push_back(str);
} else { // 如果不是则直接跳过
continue;
}
backtracking(s, i + 1); // 寻找i+1为起始位置的子串
path.pop_back(); // 回溯过程,弹出本次已经添加的子串
}注意切割过的位置,不能重复切割,所以,backtracking(s, i + 1); 传入下一层的起始位置为i + 1。
判断回文子串
最后我们看一下回文子串要如何判断了,判断一个字符串是否是回文。
可以使用双指针法,一个指针从前向后,一个指针从后向前,如果前后指针所指向的元素是相等的,就是回文字符串了。
那么判断回文的C++代码如下:
bool isPalindrome(const string& s, int start, int end) {
for (int i = start, j = end; i < j; i++, j--) {
if (s[i] != s[j]) {
return false;
}
}
return true;
}如果大家对双指针法有生疏了,传送门:双指针法:总结篇!(opens new window)
此时关键代码已经讲解完毕,整体代码如下(详细注释了)
根据Carl给出的回溯算法模板:
void backtracking(参数) {
if (终止条件) {
存放结果;
return;
}
for (选择:本层集合中元素(树中节点孩子的数量就是集合的大小)) {
处理节点;
backtracking(路径,选择列表); // 递归
回溯,撤销处理结果
}
}不难写出如下代码:
class Solution {
private:
vector<vector<string>> result;
vector<string> path; // 放已经回文的子串
void backtracking (const string& s, int startIndex) {
// 如果起始位置已经大于s的大小,说明已经找到了一组分割方案了
if (startIndex >= s.size()) {
result.push_back(path);
return;
}
for (int i = startIndex; i < s.size(); i++) {
if (isPalindrome(s, startIndex, i)) { // 是回文子串
// 获取[startIndex,i]在s中的子串
string str = s.substr(startIndex, i - startIndex + 1);
path.push_back(str);
} else { // 不是回文,跳过
continue;
}
backtracking(s, i + 1); // 寻找i+1为起始位置的子串
path.pop_back(); // 回溯过程,弹出本次已经添加的子串
}
}
bool isPalindrome(const string& s, int start, int end) {
for (int i = start, j = end; i < j; i++, j--) {
if (s[i] != s[j]) {
return false;
}
}
return true;
}
public:
vector<vector<string>> partition(string s) {
result.clear();
path.clear();
backtracking(s, 0);
return result;
}
};- 时间复杂度: O(n * 2^n)
- 空间复杂度: O(n^2)
#优化(dp判断是否是回文串)
上面的代码还存在一定的优化空间, 在于如何更高效的计算一个子字符串是否是回文字串。上述代码isPalindrome函数运用双指针的方法来判定对于一个字符串s, 给定起始下标和终止下标, 截取出的子字符串是否是回文字串。但是其中有一定的重复计算存在:
例如给定字符串"abcde", 在已知"bcd"不是回文字串时, 不再需要去双指针操作"abcde"而可以直接判定它一定不是回文字串。
具体来说, 给定一个字符串s, 长度为n, 它成为回文字串的充分必要条件是s[0] == s[n-1]且s[1:n-1]是回文字串。
大家如果熟悉动态规划这种算法的话, 我们可以高效地事先一次性计算出, 针对一个字符串s, 它的任何子串是否是回文字串, 然后在我们的回溯函数中直接查询即可, 省去了双指针移动判定这一步骤.
具体参考代码如下:
class Solution {
private:
vector<vector<string>> result;
vector<string> path; // 放已经回文的子串
vector<vector<bool>> isPalindrome; // 放事先计算好的是否回文子串的结果
void backtracking (const string& s, int startIndex) {
// 如果起始位置已经大于s的大小,说明已经找到了一组分割方案了
if (startIndex >= s.size()) {
result.push_back(path);
return;
}
for (int i = startIndex; i < s.size(); i++) {
if (isPalindrome[startIndex][i]) { // 是回文子串
// 获取[startIndex,i]在s中的子串
string str = s.substr(startIndex, i - startIndex + 1);
path.push_back(str);
} else { // 不是回文,跳过
continue;
}
backtracking(s, i + 1); // 寻找i+1为起始位置的子串
path.pop_back(); // 回溯过程,弹出本次已经添加的子串
}
}
void computePalindrome(const string& s) {
// isPalindrome[i][j] 代表 s[i:j](双边包括)是否是回文字串
isPalindrome.resize(s.size(), vector<bool>(s.size(), false)); // 根据字符串s, 刷新布尔矩阵的大小
for (int i = s.size() - 1; i >= 0; i--) {
// 需要倒序计算, 保证在i行时, i+1行已经计算好了
for (int j = i; j < s.size(); j++) {
if (j == i) {isPalindrome[i][j] = true;}
else if (j - i == 1) {isPalindrome[i][j] = (s[i] == s[j]);}
else {isPalindrome[i][j] = (s[i] == s[j] && isPalindrome[i+1][j-1]);}
}
}
}
public:
vector<vector<string>> partition(string s) {
result.clear();
path.clear();
computePalindrome(s);
backtracking(s, 0);
return result;
}
};
🌈最终代码:
回溯+双指针判断回文
class Solution {
// 存放结果的
List<List<String>> result=new LinkedList<>();
// 存放每一条路径的
List<String> path=new LinkedList<>();
public List<List<String>> partition(String s) {
// 直接回溯就好
backtracking(s,0);
//返回结果集
return result;
}
private void backtracking(String s, int startIndex){
// 如果开始分割的起始位置大于了原串的长度,那么找到了一组分割方案,递归结束,记录并返回:
if(startIndex>=s.length()){
result.add(new LinkedList<>(path));
return;
}
for(int i=startIndex;i<s.length();i++){
// 如果是回文子串,就记录
if(isPalindrome(s,startIndex,i)){
path.add(s.substring(startIndex,i+1));
}else
{
continue;
}
// 起始位置后移,保证不重复
backtracking(s,i+1);
path.removeLast();
}
}
//优美的判断回文的函数
private boolean isPalindrome(String s,int startIndex,int end){
while(startIndex<end)
if(s.charAt(startIndex++)!=s.charAt(end--))return false;
return true;
}
}
回溯+dp判断回文
class Solution {
List<List<String>> result;
LinkedList<String> path;
boolean[][] dp;
public List<List<String>> partition(String s) {
result = new ArrayList<>();
char[] str = s.toCharArray();
path = new LinkedList<>();
dp = new boolean[str.length + 1][str.length + 1];
isPalindrome(str);
backtracking(s, 0);
return result;
}
public void backtracking(String str, int startIndex) {
if (startIndex >= str.length()) {
//如果起始位置大于s的大小,说明找到了一组分割方案
result.add(new ArrayList<>(path));
} else {
for (int i = startIndex; i < str.length(); ++i) {
if (dp[startIndex][i]) {
//是回文子串,进入下一步递归
//先将当前子串保存入path
path.addLast(str.substring(startIndex, i + 1));
//起始位置后移,保证不重复
backtracking(str, i + 1);
path.pollLast();
} else {
//不是回文子串,跳过
continue;
}
}
}
}
//通过动态规划判断是否是回文串,参考动态规划篇 52 回文子串
public void isPalindrome(char[] str) {
for (int i = 0; i <= str.length; ++i) {
dp[i][i] = true;
}
for (int i = 1; i < str.length; ++i) {
for (int j = i; j >= 0; --j) {
if (str[j] == str[i]) {
if (i - j <= 1) {
dp[j][i] = true;
} else if (dp[j + 1][i - 1]) {
dp[j][i] = true;
}
}
}
}
}
}🔥今日总结:
总结
1.总体感受
这道题目在leetcode上是中等,但可以说是hard的题目了,但是代码其实就是按照模板的样子来的。
那么难究竟难在什么地方呢?
我列出如下几个难点:
- 切割问题可以抽象为组合问题
- 如何模拟那些切割线
- 切割问题中递归如何终止
- 在递归循环中如何截取子串
- 如何判断回文
我们平时在做难题的时候,总结出来难究竟难在哪里也是一种需要锻炼的能力。
一些同学可能遇到题目比较难,但是不知道题目难在哪里,反正就是很难。其实这样还是思维不够清晰,这种总结的能力需要多接触多锻炼。
本题我相信很多同学主要卡在了第一个难点上:就是不知道如何切割,甚至知道要用回溯法,也不知道如何用。也就是没有体会到按照求组合问题的套路就可以解决切割。
如果意识到这一点,算是重大突破了。接下来就可以对着模板照葫芦画瓢。
但接下来如何模拟切割线,如何终止,如何截取子串,其实都不好想,最后判断回文算是最简单的了。
关于模拟切割线,其实就是index是上一层已经确定了的分割线,i是这一层试图寻找的新分割线
除了这些难点,本题还有细节,例如:切割过的地方不能重复切割所以递归函数需要传入i + 1。
所以本题应该是一道hard题目了。
可能刷过这道题目的录友都没感受到自己原来克服了这么多难点,就把这道题目AC了,这应该叫做无招胜有招,人码合一。
2.核心代码
核心在于在横向的前提下进行纵向的遍历(DFS)。这就相当于递归的思想(或者说递归的思想在于回溯。两者不分家的。)
for (int i = startIndex; i < s.length(); i++) {
//如果是回文子串,则记录
if (isPalindrome(s, startIndex, i)) {
String str = s.substring(startIndex, i + 1);
deque.addLast(str);
} else {
continue;
}
//起始位置后移,保证不重复
backTracking(s, i + 1);
deque.removeLast();
}3.基本模版
这里的开头基本就是固定的模式了。
接口+实现===>接口为List(集合的四大天王之一)+实现LinkedList(频繁地增删使用)
// 存放结果的
List<List<String>> result=new LinkedList<>();
// 存放每一条路径的
List<String> path=new LinkedList<>();4.犯错:(引用)
详细情况请点击这里:(基础很重要的)
《JAVA核心技术卷·I》——第四章4——使用用户自定义类——《对象与类》-CSDN博客
错误
回溯结束的代码原本是这样的:
// 如果开始分割的起始位置大于了原串的长度,那么找到了一组分割方案,递归结束,记录并返回:
if(startIndex>=s.length()){
result.add(path);
return;
}这是错的,因为这里的PATH是引用,后面的更改会改变原来加入的PATH,所以这里应该传入一个新对象(深拷贝),即 new LinkedList<>(path)
修正:
应该创建一个新的 List 来复制 path 的内容再添加到 result 中,例如 result.add(new LinkedList<>(path))。
// 如果开始分割的起始位置大于了原串的长度,那么递归结束,记录并返回:
if(startIndex>=s.length()){
result.add(new LinkedList<>(path));
return;
}📣非常感谢你阅读到这里,如果这篇文章对你有帮助,希望能留下你的点赞👍 关注❤收藏✅ 评论💬,大佬三连必回哦!thanks!!!
📚愿大家都能学有所得,功不唐捐!
👇下面是专栏彩蛋系列,你会喜欢的!(为了避免影响算法的简洁与优美,这里直接将之前的几十个专栏简化为3个部分,不过你点击开后发现惊喜。)👇
💖💖💖💖💖💖💖💖💖💖💖💖💖💖💖💖💖💖
热门专栏
💖💖💖💖💖💖💖💖💖💖💖💖💖💖💖💖💖💖