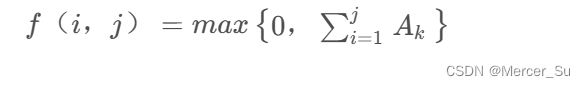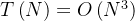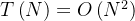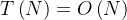1.3 实用应例:最大子序列
1.3.1 题目
给定N个整数的序列{A1 , A2 , ……,AN},求函数 的最大值,若值为负数,则放回0
1.3.1 暴力算法
1.3.1 方法1
思路:算出每个子序列的和
int fun1(int a[],int n){
int ThisSum,MaxSum=0;
for(int i=0;i<n;i++){ /*i是左端位置*/
for(int j=n;j>i;j--){ /*j是右端位置*/
ThisSum=0;
for(int k=i;k<j;k++){
ThisSum+=a[k];/*从1~5,2~5,3~5,……*/
if(ThisSum>MaxSum) MaxSum=ThisSum;
}
}
}
if(MaxSum<0) MaxSum=0;
return MaxSum;
}缺点:每次都会再次计算前面计算过的子序列和
时间复杂度:因为三重循环,且每次循环均接近N
所以时间复杂度为:
1.3.1 方法二(暴力优化)
思路:重新计算的部分省略
int fun2(int a[],int n){
int ThisSum,MaxSum=0;
for(int i=0;i<n;i++){/*i是左端位置*/
ThisSum=0;
for(int j=i;j<n;j++){/*j是右端位置*/
ThisSum+=a[j];/*从1~5,2~5,3~5,……*/
if(ThisSum>MaxSum) MaxSum=ThisSum;
}
if(MaxSum<0) MaxSum=0;
}
return MaxSum;
}时间复杂度:两重循环,且每次循环均接近N
所以时间复杂度为
1.3.1 分治(分而治之)
思路:
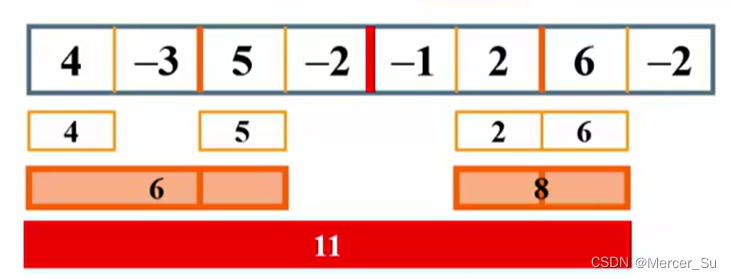
分:将数据分为左右两块,再左右两边以此递归(再次分为左右两边),足够小,求出当前最大
治:跨越边界,求出最大,从中间位置向两边扫描 三者相比较,求出最大的值
int cross_sum(int a[],int left,int right,int mid){
if(left==right) return a[left];
int leftsum=INT_MIN;/*int能找到的最小值*/
int Thissum=0;
for(int i=mid;i>left-1;i--){/*中点向左侧遍历,最大子序列和*/
Thissum+=a[i];
leftsum=max(leftsum,Thissum);
}
int rightsum=INT_MIN;
Thissum=0;
for(int i=mid+1;i<right+1;i++){/*中点向右侧遍历,最大子序列和*/
Thissum+=a[i];
rightsum=max(Thissum,rightsum);
}
return (leftsum+rightsum);
}
int fun3(int a[],int left,int right){
if(left==right) return a[left];
int LeftSum,RightSum,CrossSum;
int mid=(left+right)/2;
LeftSum=fun3(a,left,mid);/*确定左边的最大子序列*/
RightSum=fun3(a,mid+1,right);/*确定右边最大子序列*/
CrossSum=cross_sum(a,left,right,mid);/*跨越边界的子序列和*/
return max(max(LeftSum,RightSum),CrossSum);
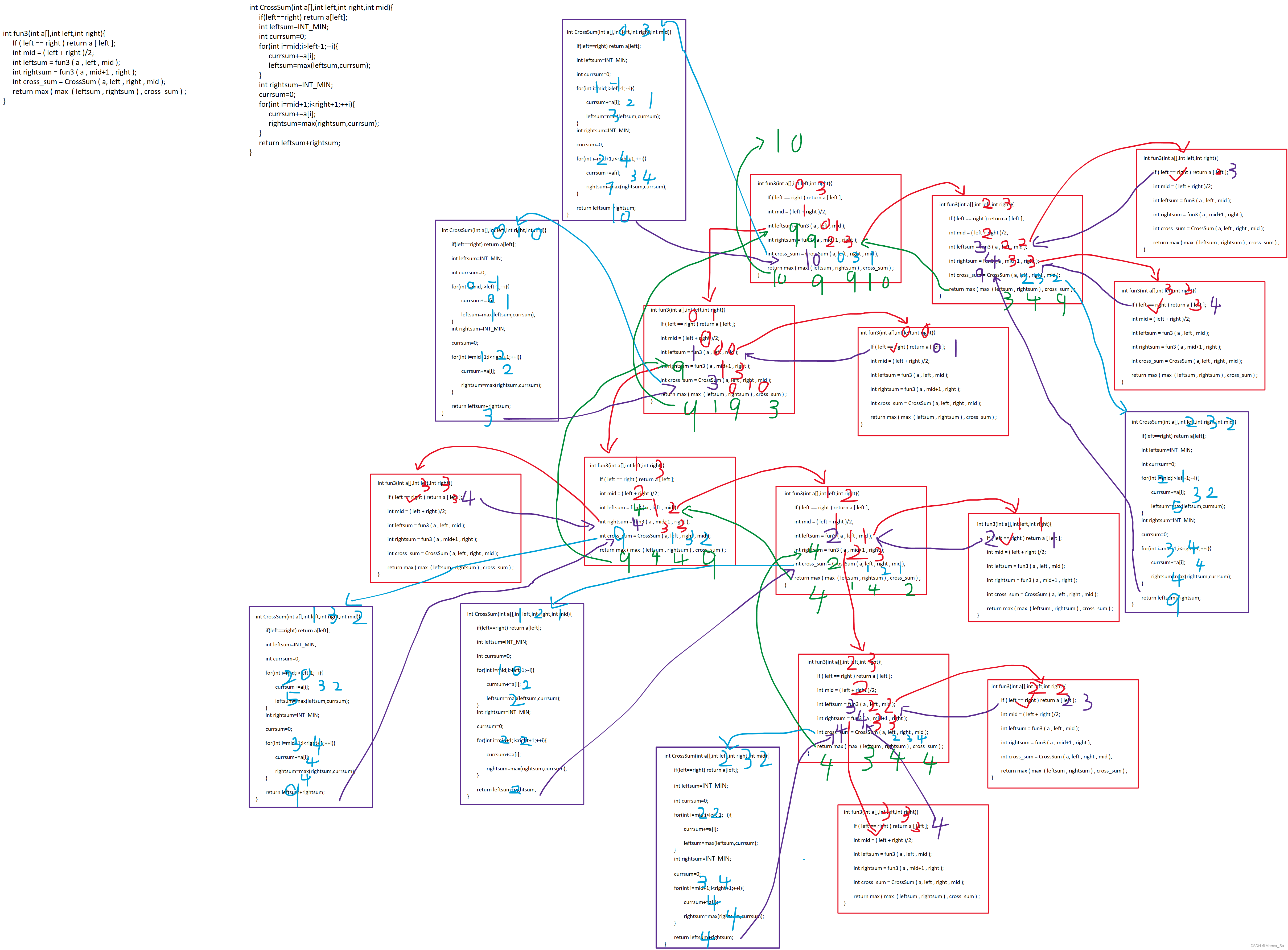
}程序运行过程:
时间复杂度:
其中乘以2^k,前得N,k为logN,以2为底的logN
所以
相加取最大,时间复杂度为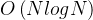
1.3.1 在线处理法
思路:当前子序列和为负数时,不会为后续子序列和提供价值,舍弃,保证当前答案的正确性
int fun(int a[],int n){
int ThisSum=0,MaxSum=0;
for(int i=0;i<n;i++){
ThisSum+=a[i];
if(ThisSum>MaxSum) MaxSum=ThisSum;
else if(ThisSum<0) ThisSum=0;/*小于0无法为后面提供价值*/
}
return MaxSum;
}时间复杂度:一个for循环,循环里面的所有东西包括if—else 都是常数量级的复杂度
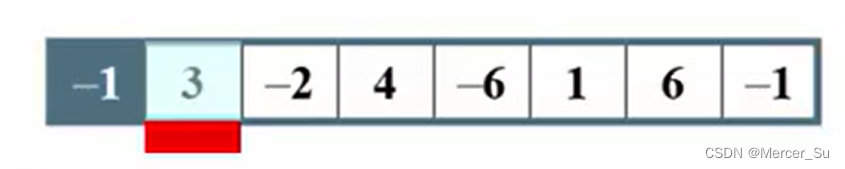
第一个数字:-1 , 使得ThisSum=-1<0 , 没有价值,舍弃
第二个数字:3 ,使得使得ThisSum=3>MaxSum , MaxSum=3
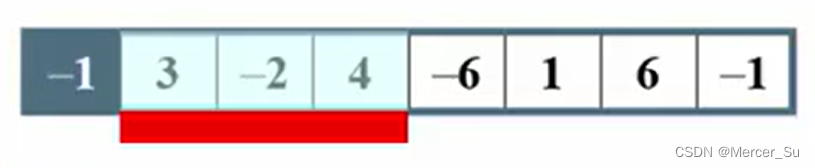
第三个数字:-2,使得ThisSum=1<MaxSum , 不更新,MaxSum=3
第四个数字:4,使得ThisSum=5>MaxSum , 更新 , MaxSum=5
以此类推,保证当前绝对正确
在线的意思是指每输入一个数据就即时处理,在任何一个地方中止输入,算法都能给出正确的、当前的解