一、机器学习
1.1 机器学习定义
1.2 监督学习 supervised learning
1.2.1 监督学习定义
给算法一个数据集,其中包含了正确答案,算法的目的是给出更多的正确答案
如预测房价(回归问题)、肿瘤良性恶性分类(分类问题)
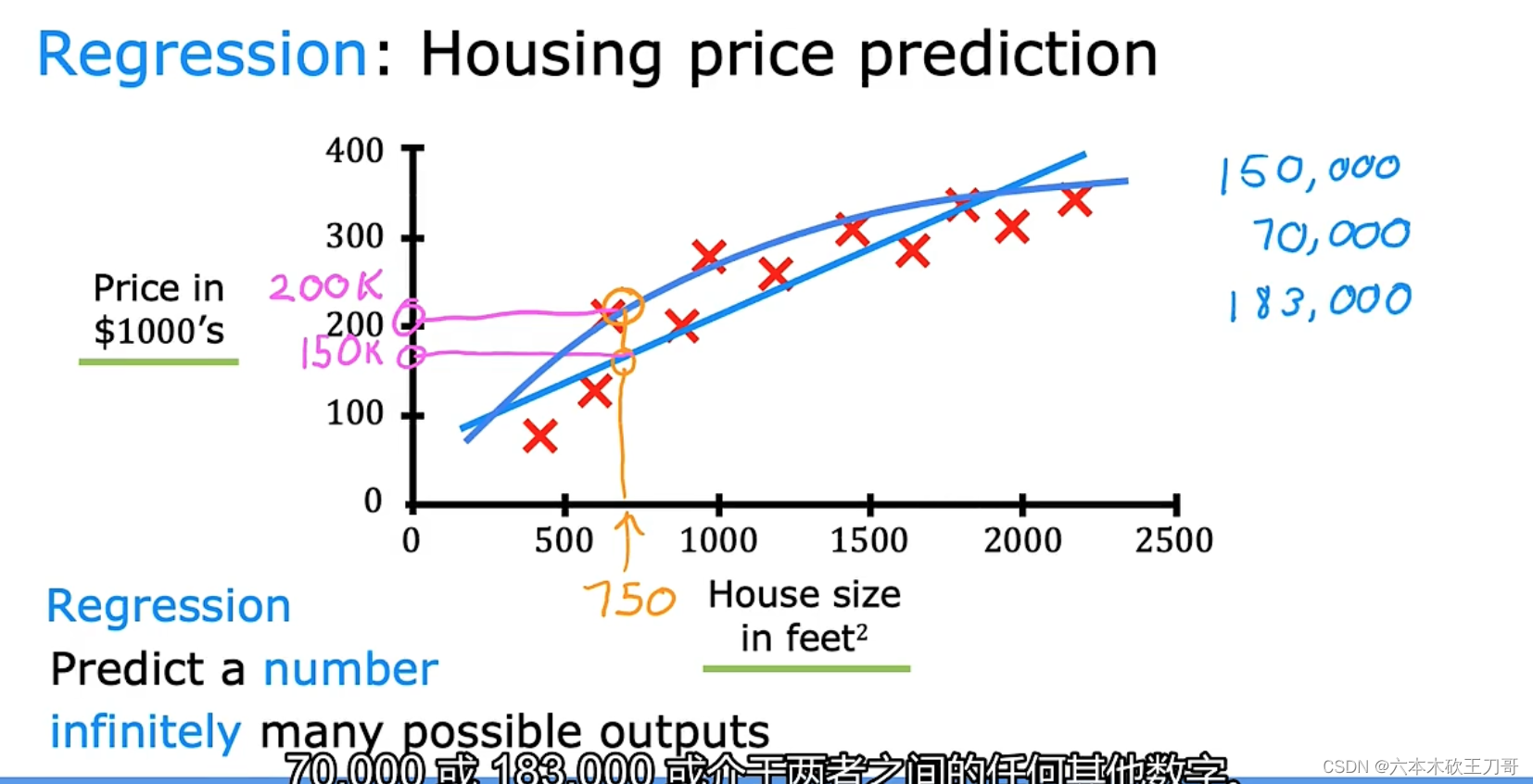
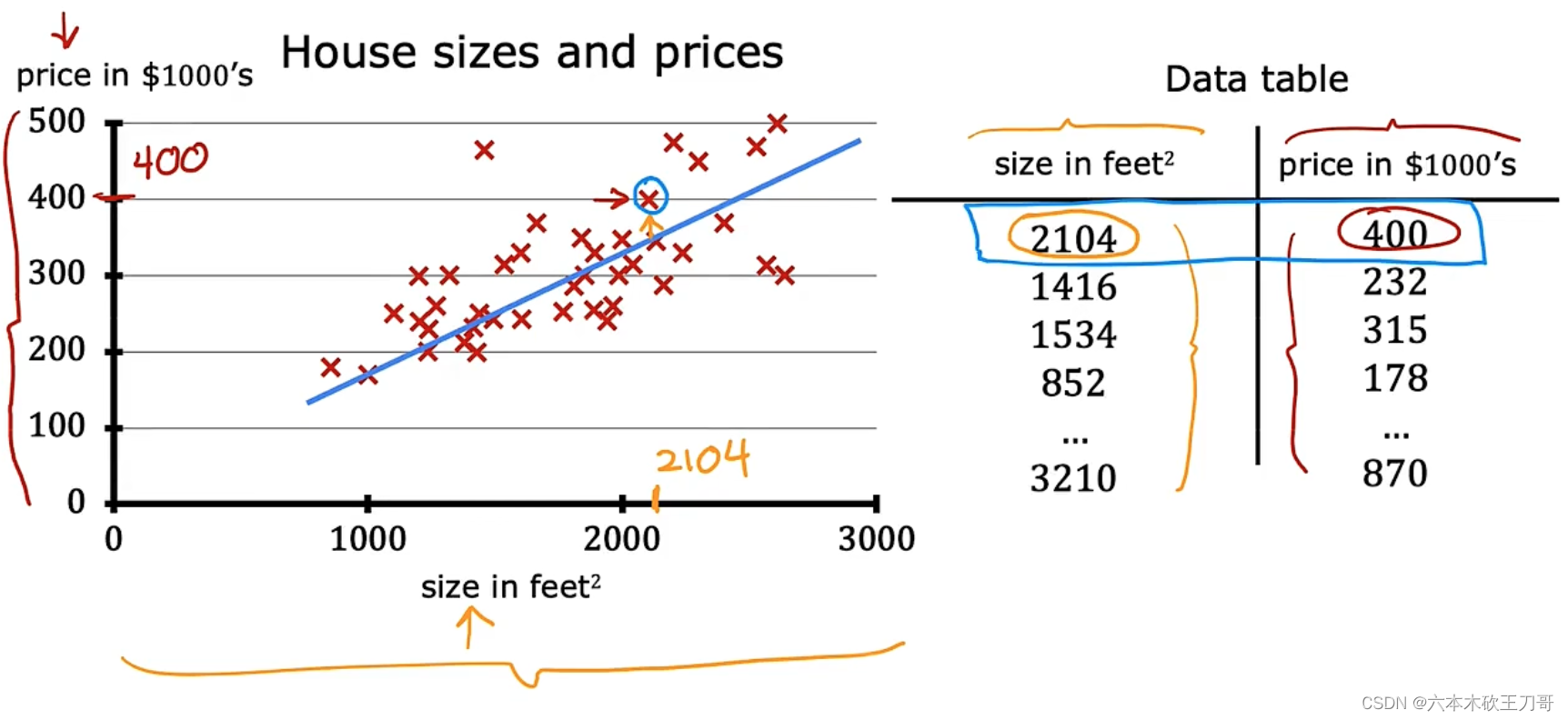
假如说你想预测房价。前阵子,一个学生从波特兰俄勒冈州的研究所收集了一些房价的数据。你把这些数据画 出来,看起来是这个样子:横轴表示房子的面积,单位是平方英尺,纵轴表示房价,单位是千美元。那基于这组数据,假如你有一个朋友,他有一套 750 平方英尺房子,现在他希望把 房子卖掉,他想知道这房子能卖多少钱。那么关于这个问题,机器学习算法将会怎么帮助你呢?
我们应用学习算法,可以在这组数据中画一条直线,或者换句话说,拟合一条直线,根据这条线我们可以推测出,这套房子可能卖$150,000,当然这不是唯一的算法。可能还有更 好的,比如我们不用直线拟合这些数据,用二次方程去拟合可能效果会更好。根据二次方程的曲线,我们可以从这个点推测出,这套房子能卖接近$200,000。稍后我们将讨论如何选择学习算法,如何决定用直线还是二次方程来拟合。两个方案中有一个能让你朋友的房子出售得更合理。这些都是学习算法里面很好的例子。以上就是监督学习的例子。
可以看出,监督学习指的就是我们给学习算法一个数据集。这个数据集由“正确答案”组成。在房价的例子中,我们给了一系列房子的数据,我们给定数据集中每个样本的正确价格, 即它们实际的售价然后运用学习算法,算出更多的正确答案。比如你朋友那个新房子的价格。用术语来讲,这叫做回归问题。我们试着推测出一个连续值的结果,即房子的价格。
再举另外一个监督学习的例子。我和一些朋友之前研究过这个。假设说你想通过查看病历来推测乳腺癌良性与否,假如有人检测出乳腺肿瘤,恶性肿瘤有害并且十分危险,而良性的肿瘤危害就没那么大,所以人们显然会很在意这个问题。
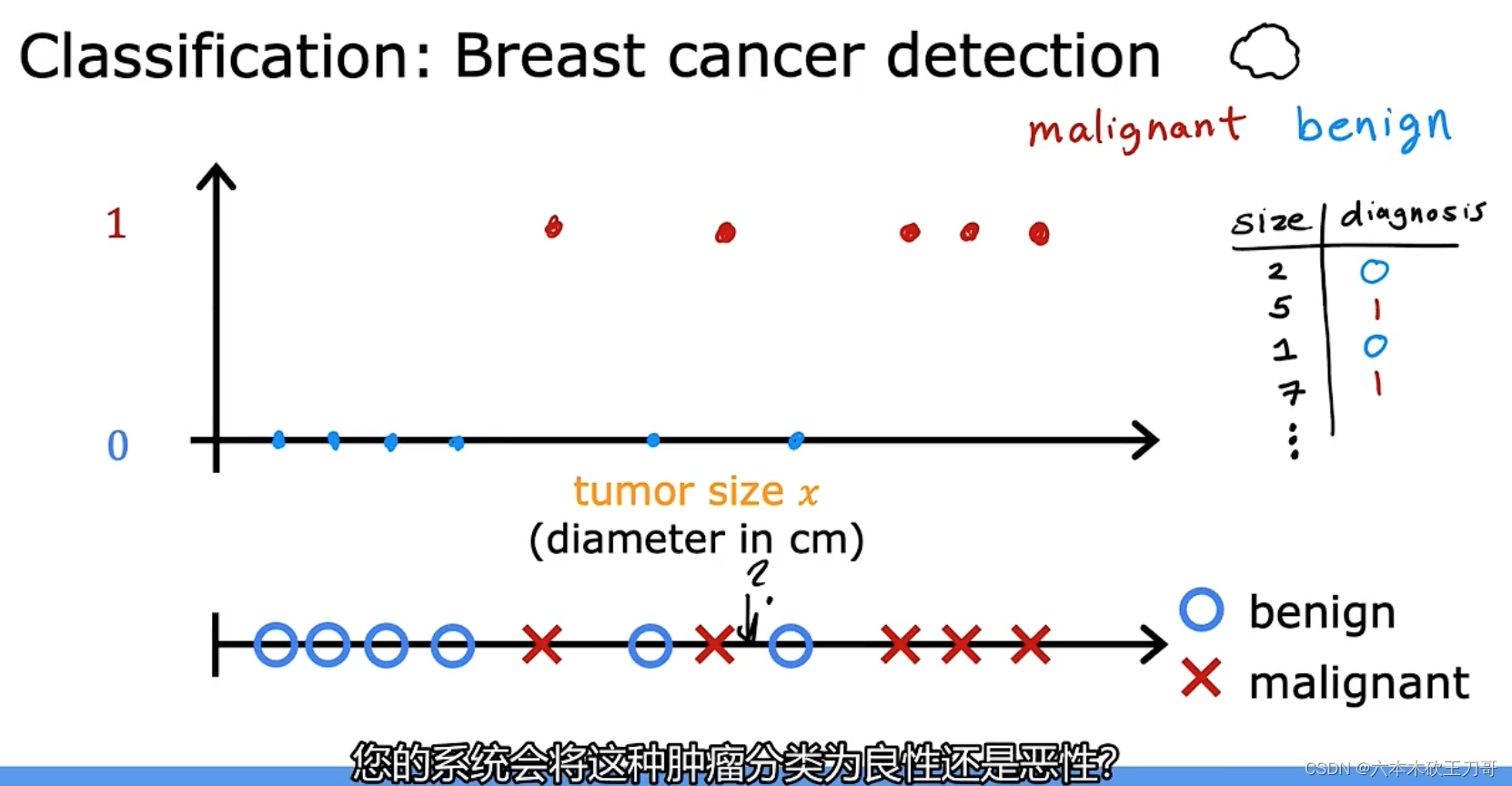
让我们来看一组数据:这个数据集中,横轴表示肿瘤的大小,纵轴上,我标出 1 和 0 表示是或者不是恶性肿瘤。我们之前见过的肿瘤,如果是恶性则记为 1,不是恶性,或者说良性记为 0。
我有 5 个良性肿瘤样本,在 1 的位置有 5 个恶性肿瘤样本。现在我们有一个朋友很不幸 检查出乳腺肿瘤。假设说她的肿瘤大概这么大,那么机器学习的问题就在于,你能否估算出肿瘤是恶性的或是良性的概率。用术语来讲,这是一个分类问题。
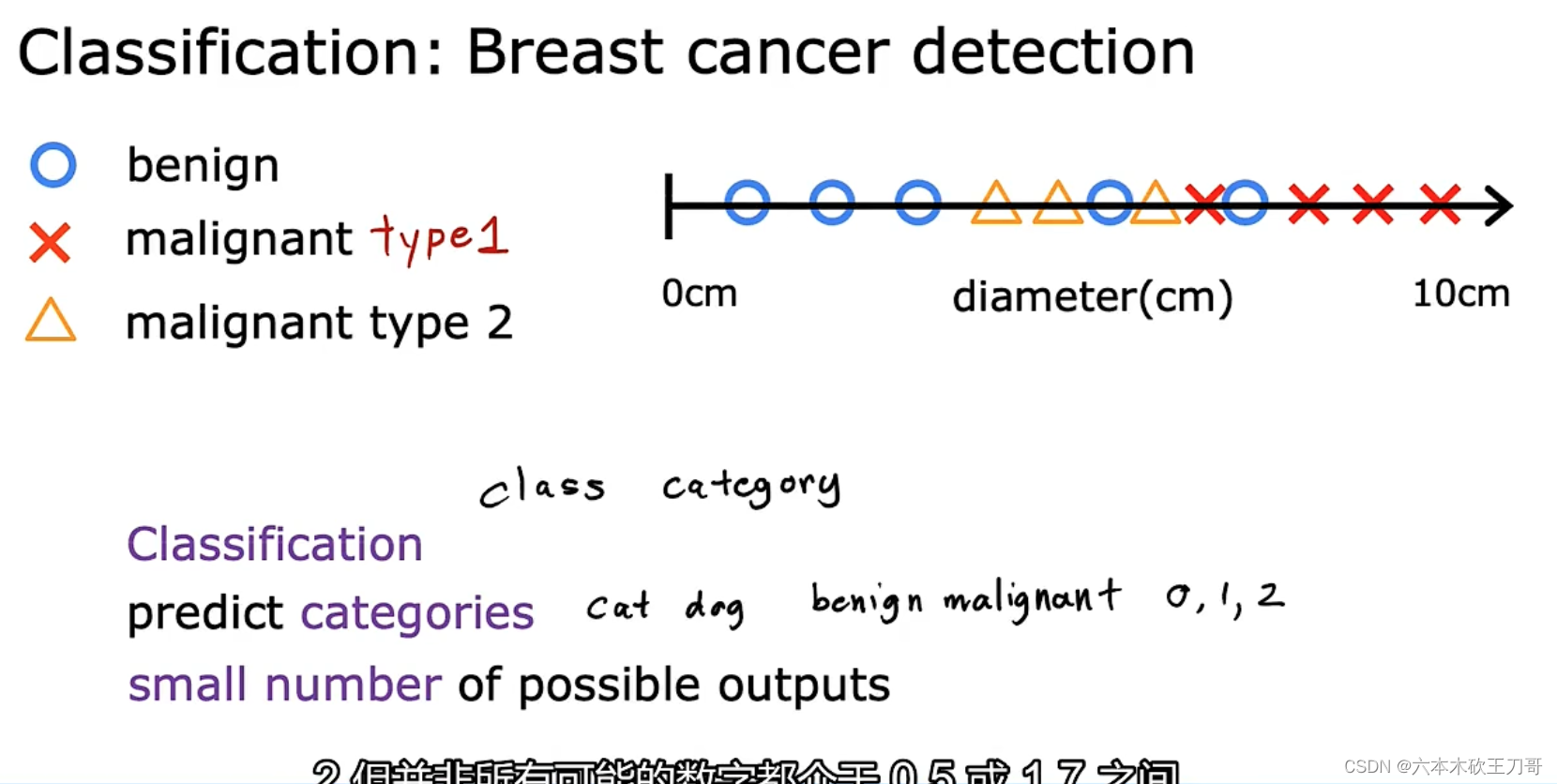
分类指的是,我们试着推测出离散的输出值:0 或 1 良性或恶性,而事实上在分类问题 中,输出可能不止两个值。比如说可能有三种乳腺癌,所以你希望预测离散输出 0、1、2、 3。0 代表良性,1 表示第 1 类乳腺癌,2 表示第 2 类癌症,3 表示第 3 类,但这也是分类问 题。
因为这几个离散的输出分别对应良性,第一类第二类或者第三类癌症,在分类问题中我们可以用另一种方式绘制这些数据点。
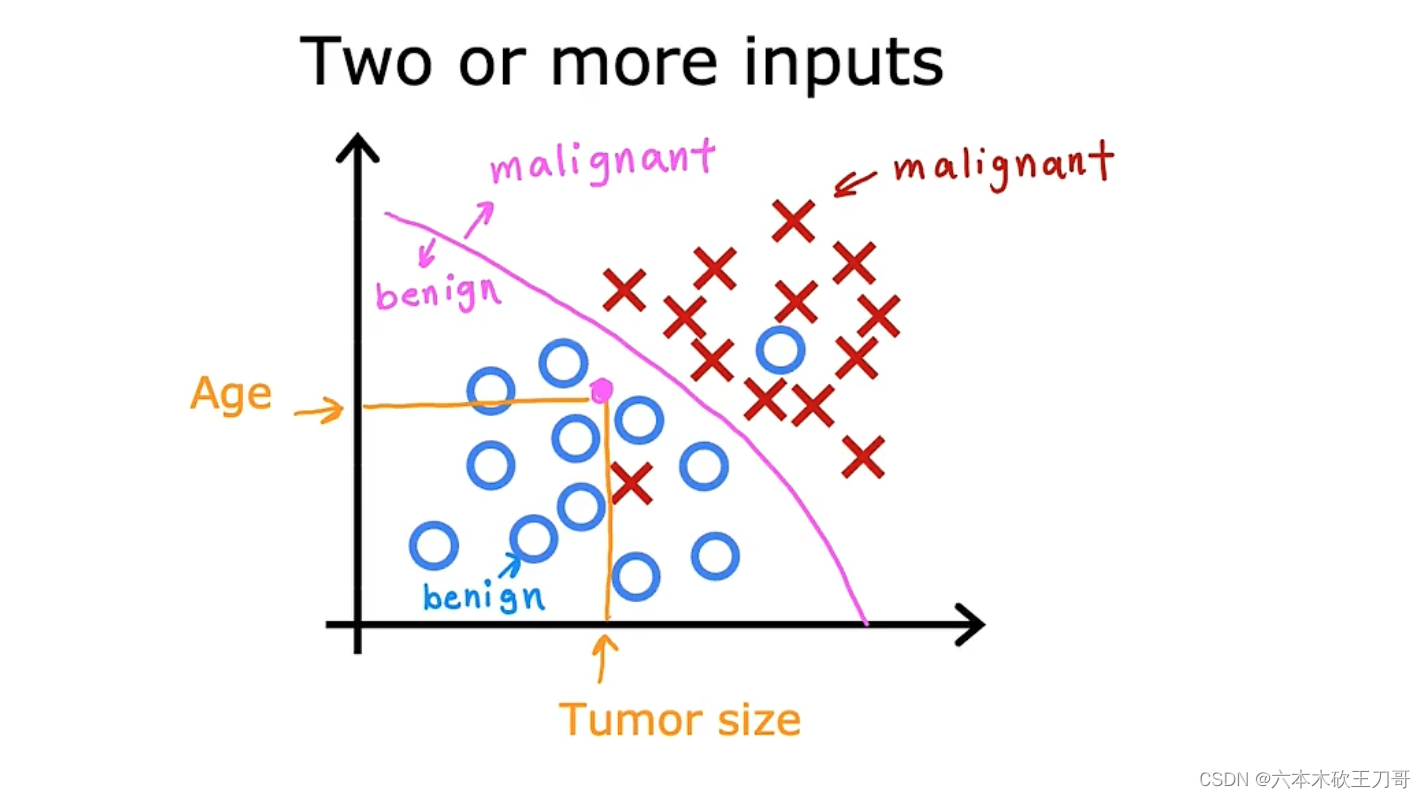
在其它一些机器学习问题中,可能会遇到不止一种特征。举个例子,我们不仅知道肿瘤的尺寸,还知道对应患者的年龄。在其他机器学习问题中,我们通常有更多的特征,我朋友研究这个问题时,通常采用这些特征,比如肿块密度,肿瘤细胞尺寸的一致性和形状的一致性等等,还有一些其他的特征。这就是我们即将学到最有趣的学习算法之一。
1.3 无监督学习 unsupervised learning
1.3.1 无监督学习定义
只给算法一个数据集,但是不给数据集的正确答案,由算法自行分类。
如聚类
1.谷歌新闻每天收集几十万条新闻,并按主题分好类
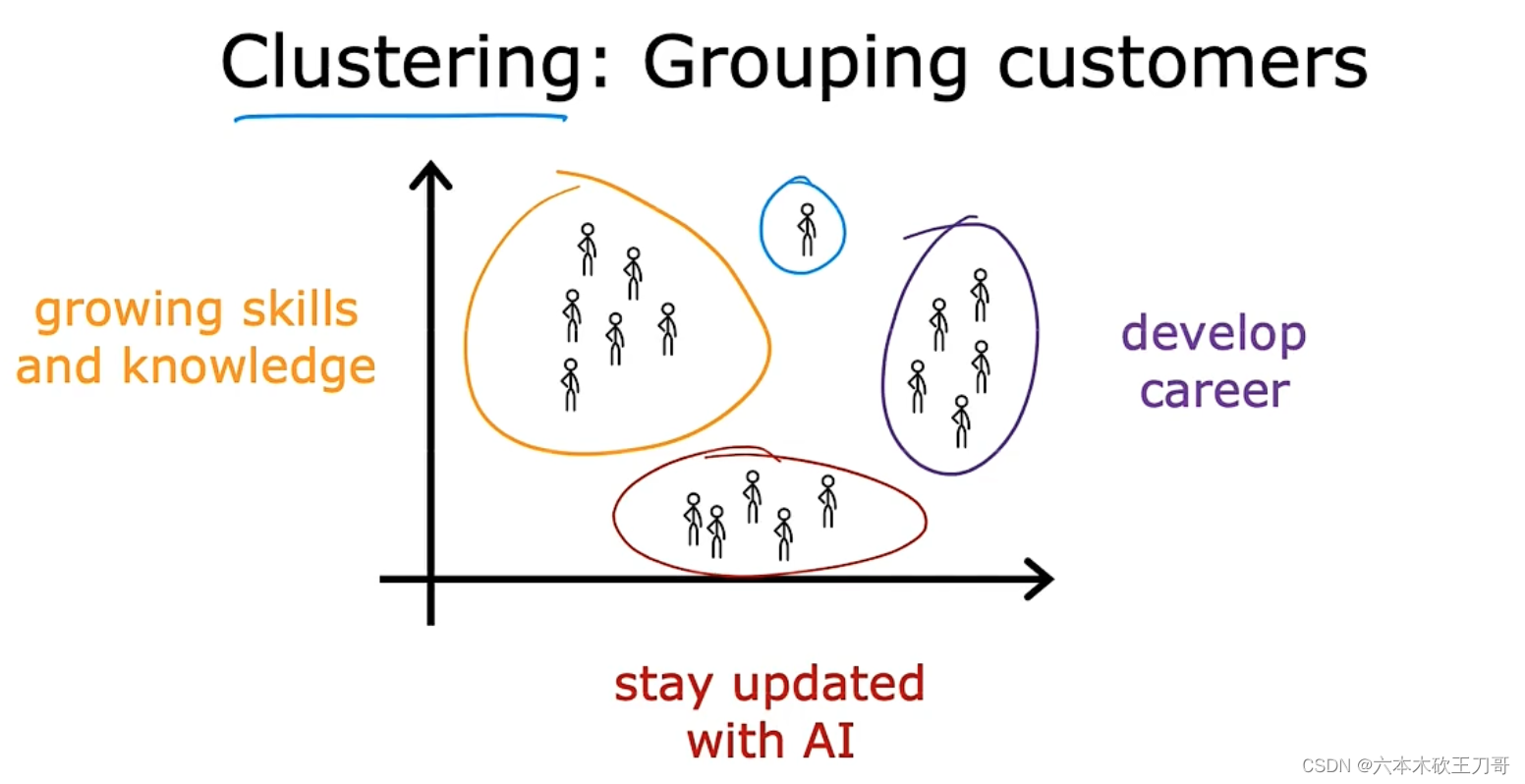
2.Grouping customer 市场通过对用户进行分类,确定目标用户
1.3.2 聚类算法
二、单变量的线性回归 univariate linear regression——预测问题
2.1 线性回归模型
这个例子是预测住房价格的,我们要使用一个数据集,数据集包含俄勒冈州波特兰市的住房价格。它被称作监督学习是因为对于每个数据来说,我们给出了“正确的答案”,即告诉我们: 根据我们的数据来说,房子实际的价格是多少,而且,更具体来说,这是一个回归问题。回 归一词指的是,我们根据之前的数据预测出一个准确的输出值,对于这个例子就是价格。
我们将要用来描述这个回归问题的标记如下: 𝑚 代表训练集中实例的数量
𝑥 代表特征/输入变量
𝑦 代表目标变量/输出变量
(𝑥,𝑦) 代表训练集中的实例
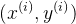
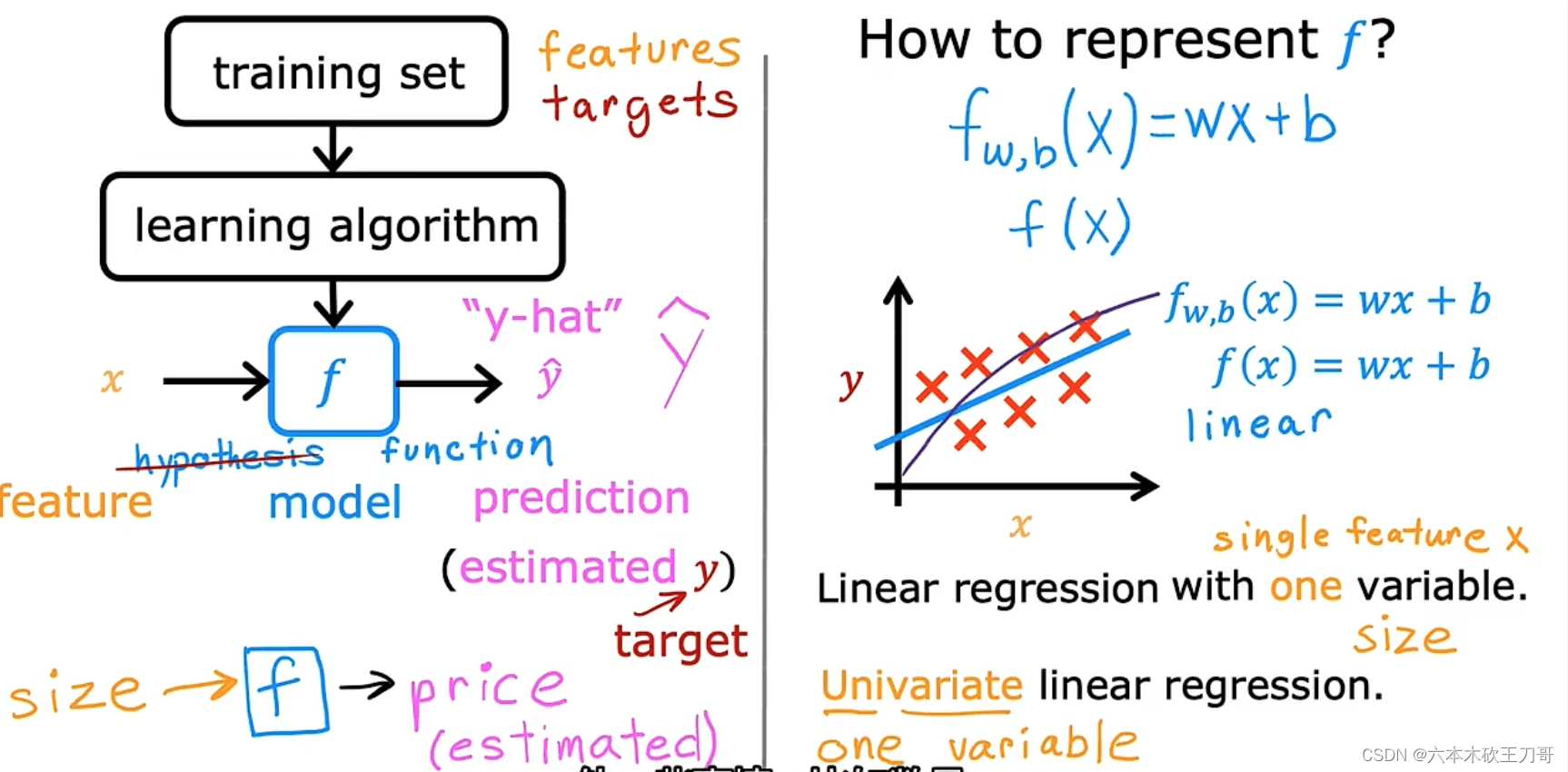
训练算法在这里是一个函数f,输入feature x,输出估计值y-hat,y-hat并不一定等于真实值。在线性回归中,f是用wx+b表示的,因为只含有一个特征/输入变量,因此这样的问题叫作单变量线性回归问题。
2.2 代价函数
2.2.1 代价函数推导
定义代价函数的概念,这有助于我们弄清楚如何把最有可能的直线与我们的数据相拟合。
在单变量线性回归模型中,需要明确w和b的作用是什么,也就是为我们的模型选择合适的参数w和b,在房价问题这个例子中便是直线的斜率和在𝑦 轴上的截距。
我们选择的参数决定了我们得到的直线相对于我们的训练集的准确程度,模型所预测的值y(i)-hat与训练集中实际值y(i)之间的差距就是建模误差(modeling error)。我们的目标便是选择出可以使得建模误差的平方和能够最小的模型参数。
cost function函数就是根据全部实际值和预测值之差的平方和推导出。
2.2.2 理解代价函数
我们给了代价函数一个数学上的定义。在这个视频里,让我们通过一些例子来获取一些直观的感受,看看代价函数到底是在干什么。 首先需要明确目标是最小化代价函数,并找出最小化代价函数的参数(单变量线性回归中是w和b)。
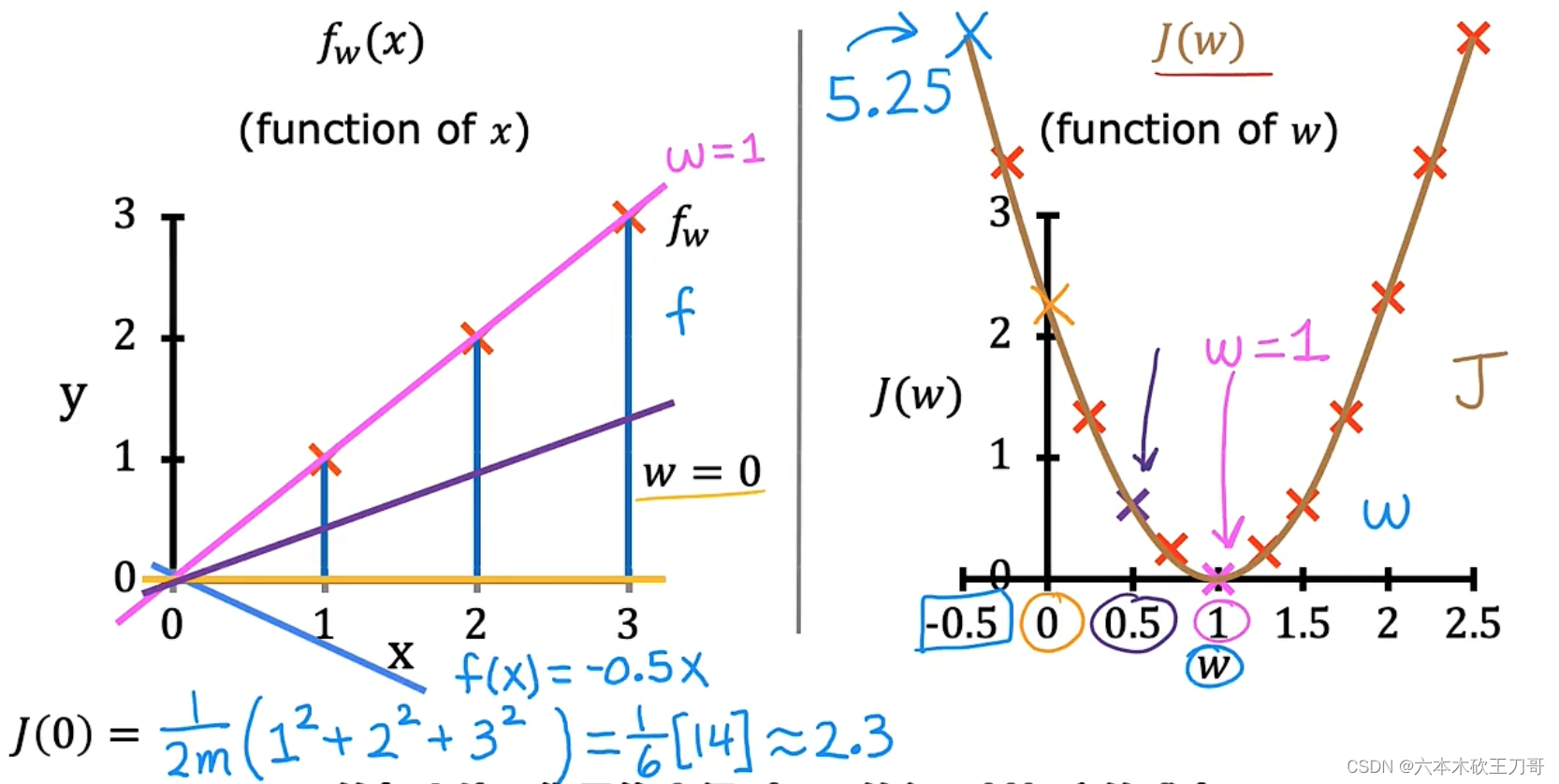
假设目前的变量只有w,可以推导出简化版的代价函数。
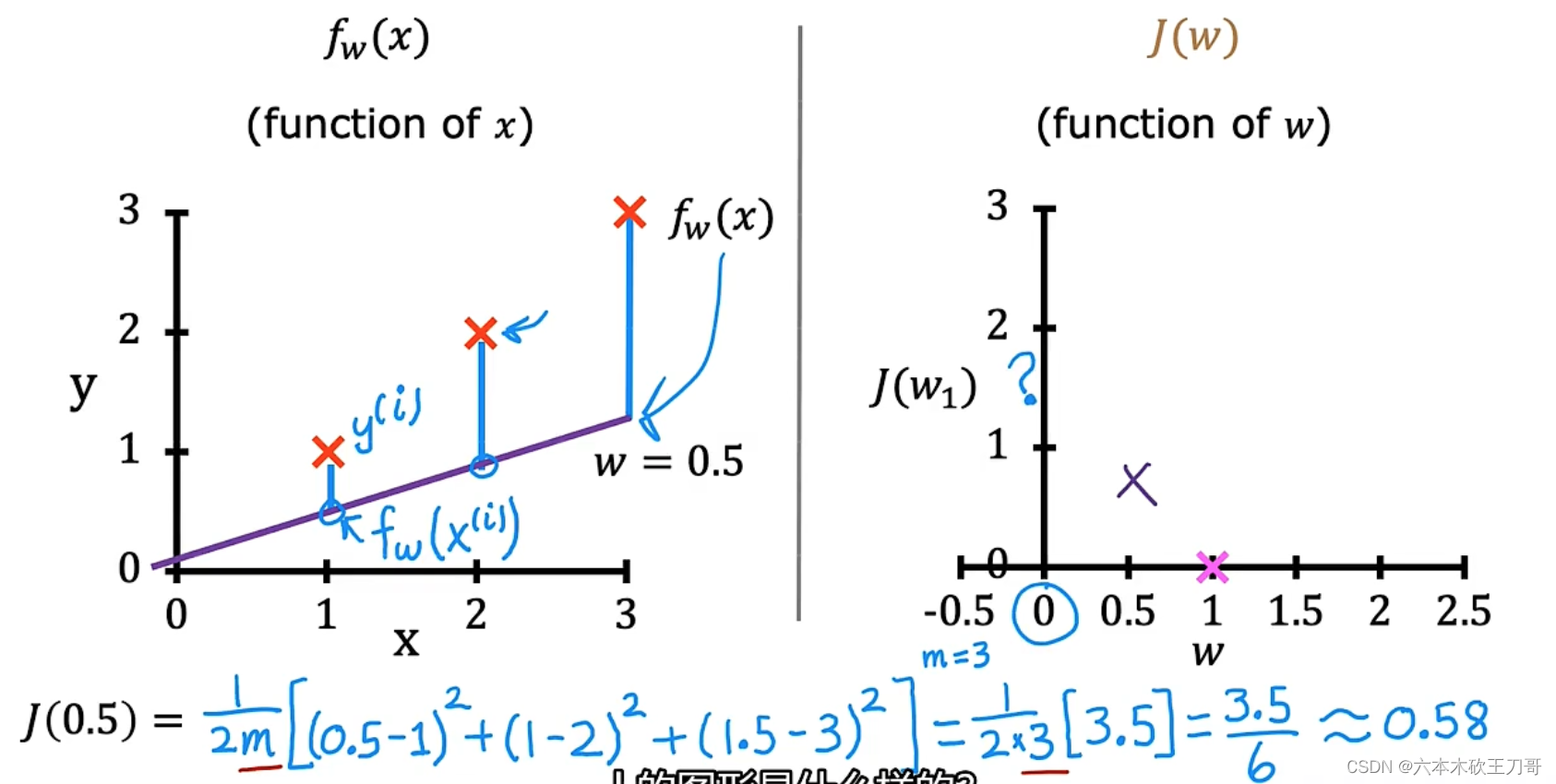
现在开始绘制J(w)的图像,假设训练集的数据如下左图所示,当w等于1时,J(w) = 0。
继续绘制J(w)的图像,当w=0.5时,可以计算出J(w)的值,并把点标在图像上。
测试完一系列点,最终的代价函数可视化图像如下所示,当w=1时,代价函数最小。
2.2.3 可视化代价函数
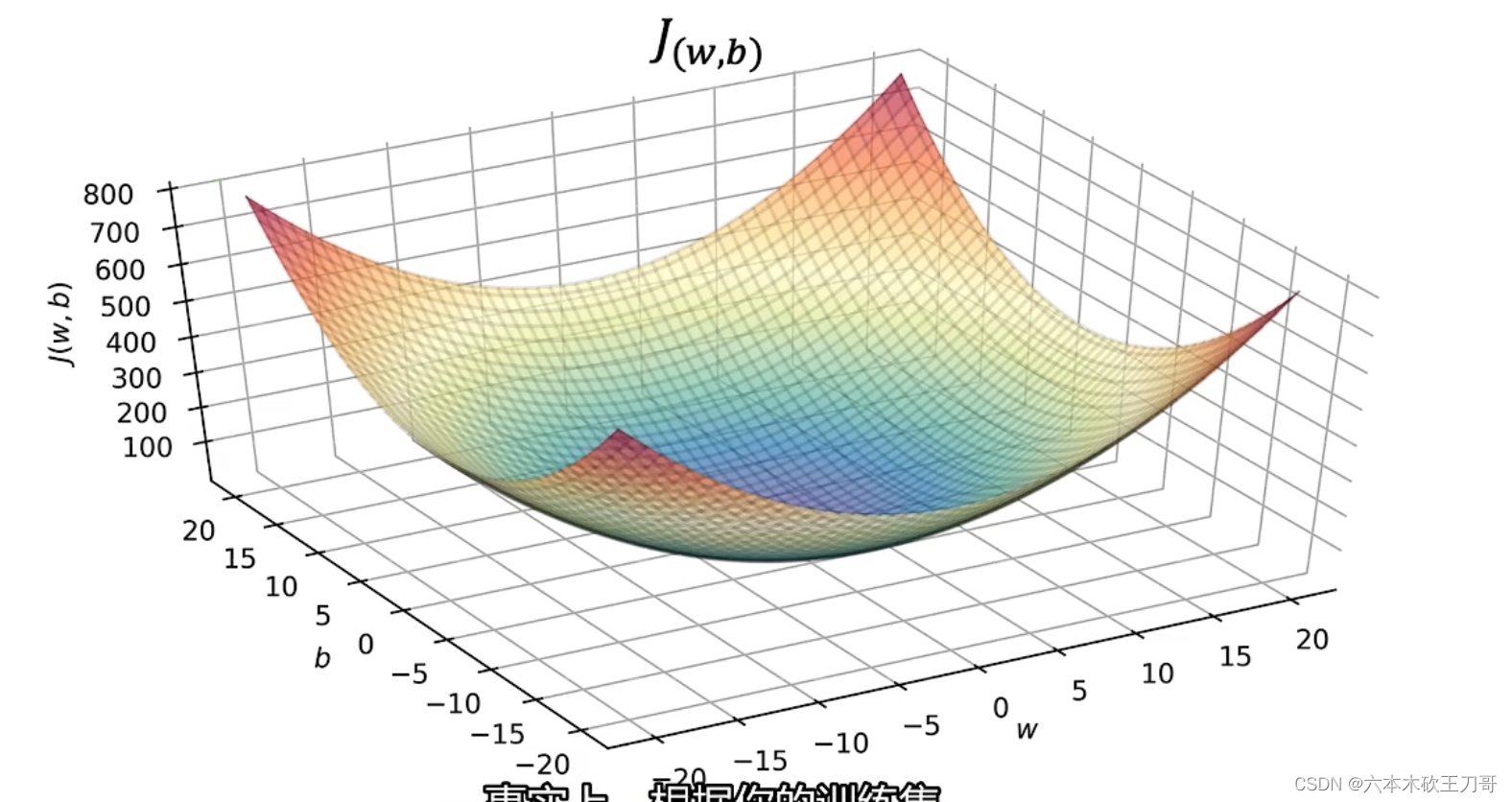
包含w和b参数并且更general的代价函数可视化图像是一个类似碗状的三维图像。
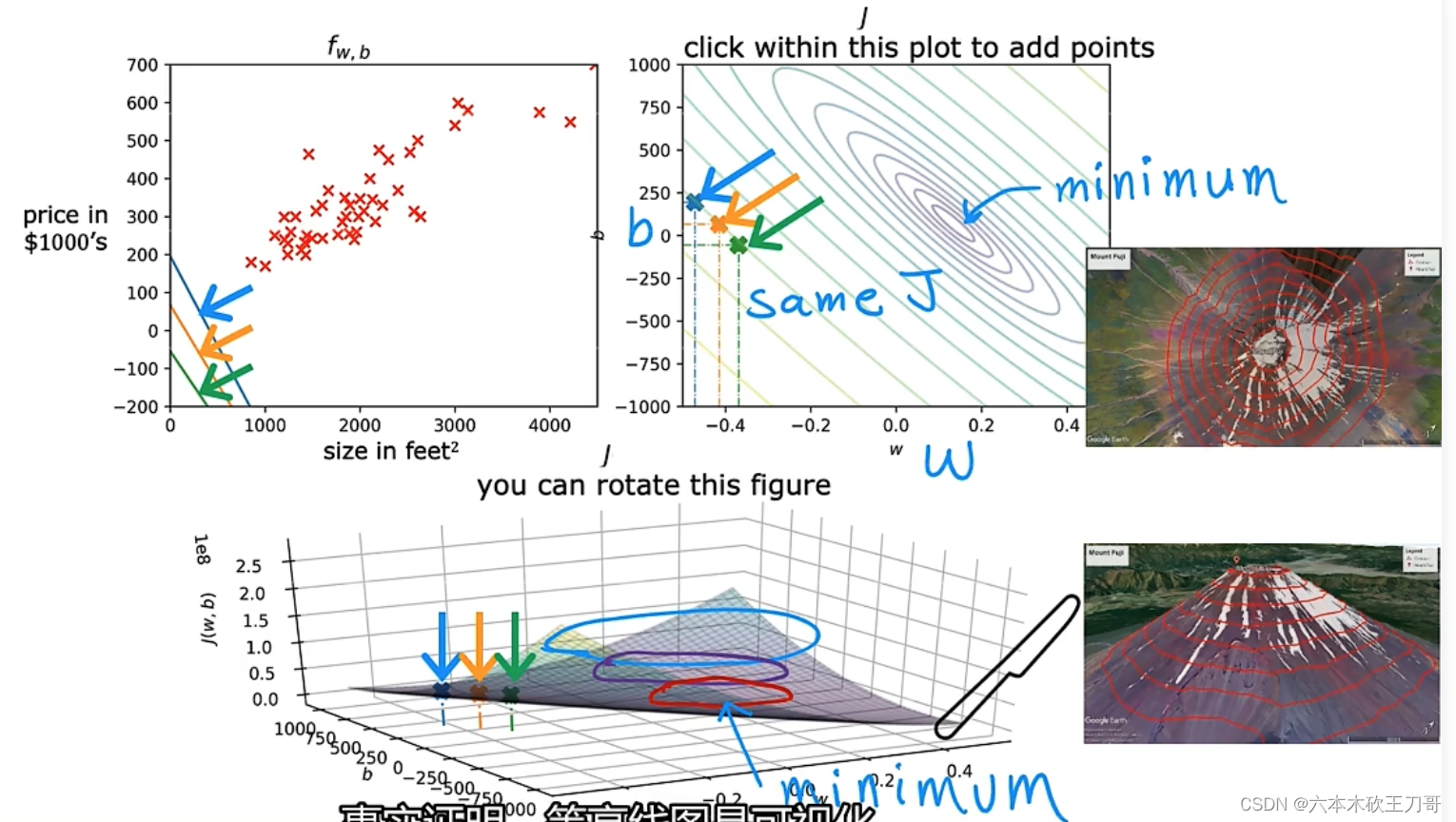
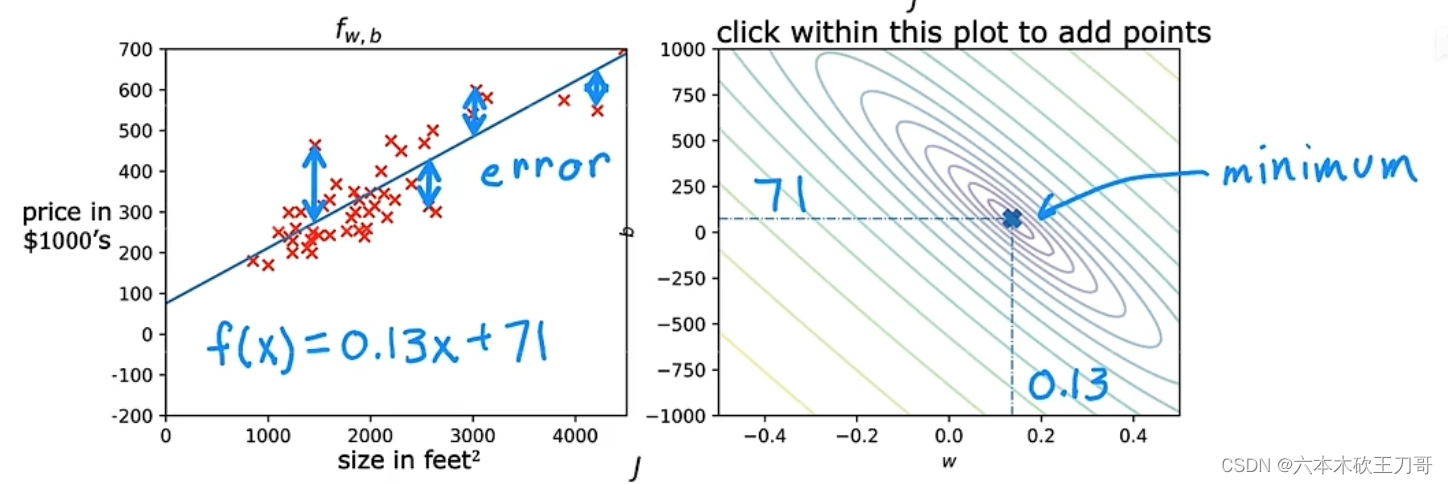
另一种代价函数的样子,是等高线图,这个图是最下面三维图像的等高线图。可以看出在三维空间中存在一个使得J(w, b)最小的点,对应等高线图中是minimum的中心点,
我们们也不希望编个程序把这些点画出来,然后人工的方法来读出这些点的数值,这很明显不是一个好办法。我们会遇到更复杂、更高维度、更多参数的情况,而这些情况是很难画出图的,因此更无法将其可视化,因此我们真正需要的是编写程序来找出这些最小化代价函数的w和b的值。
2.2.4 可视化举例
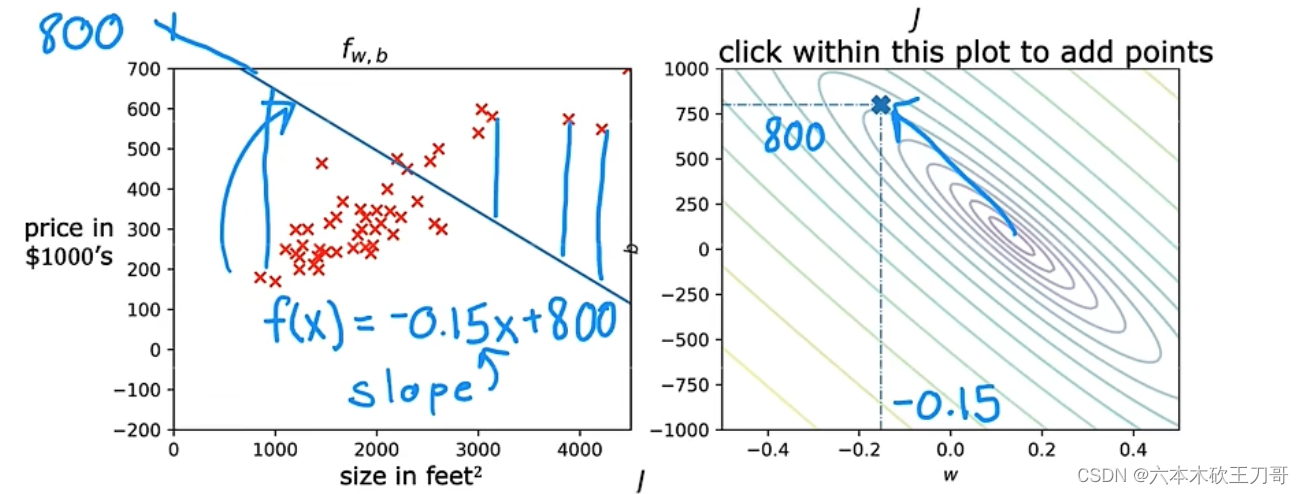
现在来看几个例子,帮助更好的理解单变量线性函数和它的代价函数之间的关系,分别取不同的w和b,对应等高线图中的不同位置,越靠近中心点,拟合的效果越好。
2.3 梯度下降算法 Gradient Descent algorithm
2.3.1 梯度下降算法的实现
梯度下降是一个用来求函数最小值的算法,我们将使用梯度下降算法来求出代价函数 𝐽(w,b) 的最小值。
梯度下降背后的思想是:开始时我们随机选择一个参数的组合(w,b),计算代价函数,然后我们寻找下一个能让代价函数值下降最多的参数组合。我们持续这么做直到一个局部最小值(local minimum),因为我们并没有尝试完所有的参数组合,所以不能确定我们得到的局部最小值是否便是全局最小值(global minimum),选择不同的初始参数组合,可能会找到不同的局部最小值。
想象一下你正站立在山的这一点上,站立在你想象的公园这座红色山上,在梯度下降算法中,我们要做的就是旋转 360 度,看看我们的周围,并问自己要在某个方向上,用小碎步尽快下山。这些小碎步需要朝什么方向?如果我们站在山坡上的这一点,你看一下周围,你会发现最佳的下山方向,你再看看周围,然后再一次想想,我应该从什么方向迈着小碎步下山?然后你按照自己的判断又迈出一步,重复上面的步骤,从这个新的点,你环顾四周,并决定从什么方向将会最快下山,然后又迈进了一小步,并依此类推,直到你接近局部最低点的位置。
批量梯度下降(batch gradient descent)算法的公式为:
其中𝑎是学习率(learning rate),它决定了我们沿着能让代价函数下降程度最大的方向向下迈出的步子有多大,在批量梯度下降中,我们每一次都同时让所有的参数减去学习速率乘以代价函数的导数。
在梯度下降算法中,这是正确实现同时更新的方法。我不打算解释为什么你需要同时更新,同时更新是梯度下降中的一种常用方法。我们之后会讲到,同步更新是更自然的实现方法。当人们谈到梯度下降时,他们的意思就是同步更新。
2.3.2 理解梯度下降算法
对w赋值,使得𝐽(w)按梯度下降最快方向进行,一直迭代下去,最终得到局部最小值。其中𝑎是学习率(learning rate),它决定了我们沿着能让代价函数下降程度最大的方向向下迈出的步子有多大。
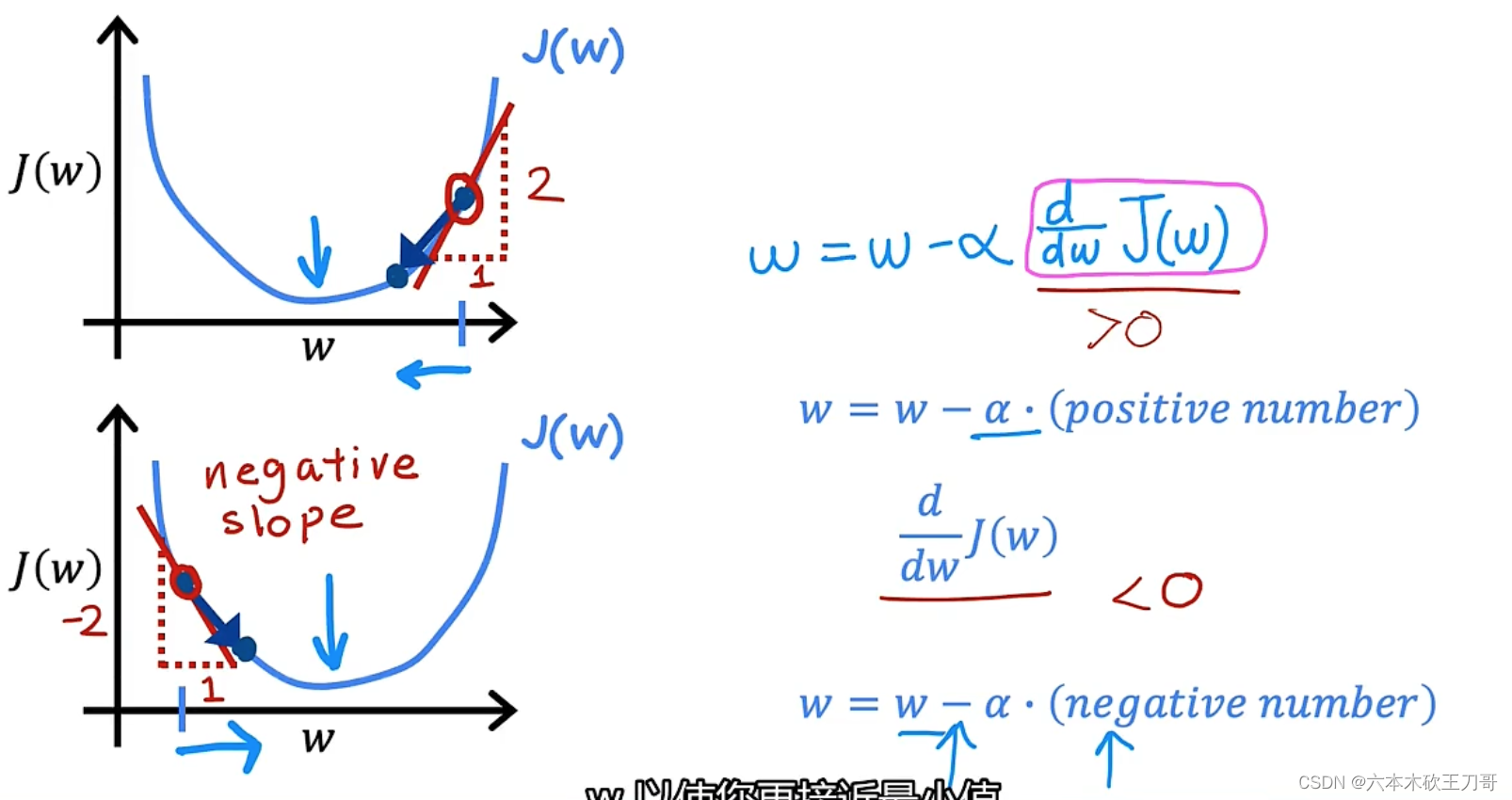
对于这个问题,求导的目的,基本上可以说取这个红点的切线,就是这样一条红色的直线,刚好与函数相切于这一点,让我们看看这条红色直线的斜率,就是这条刚好与函数曲线相切的这条直线,这条直线的斜率正好是这个三角形的高度除以这个水平长度。
分两种情况讨论,这条线有一个正斜率,也就是说它有正导数,因此,我得到的新的w,w更新后等于w减去一个正数乘以𝑎。另外一种情况负斜率,也就是负导数,此时w更新是w加上一个正数乘𝑎。
2.3.3 学习率
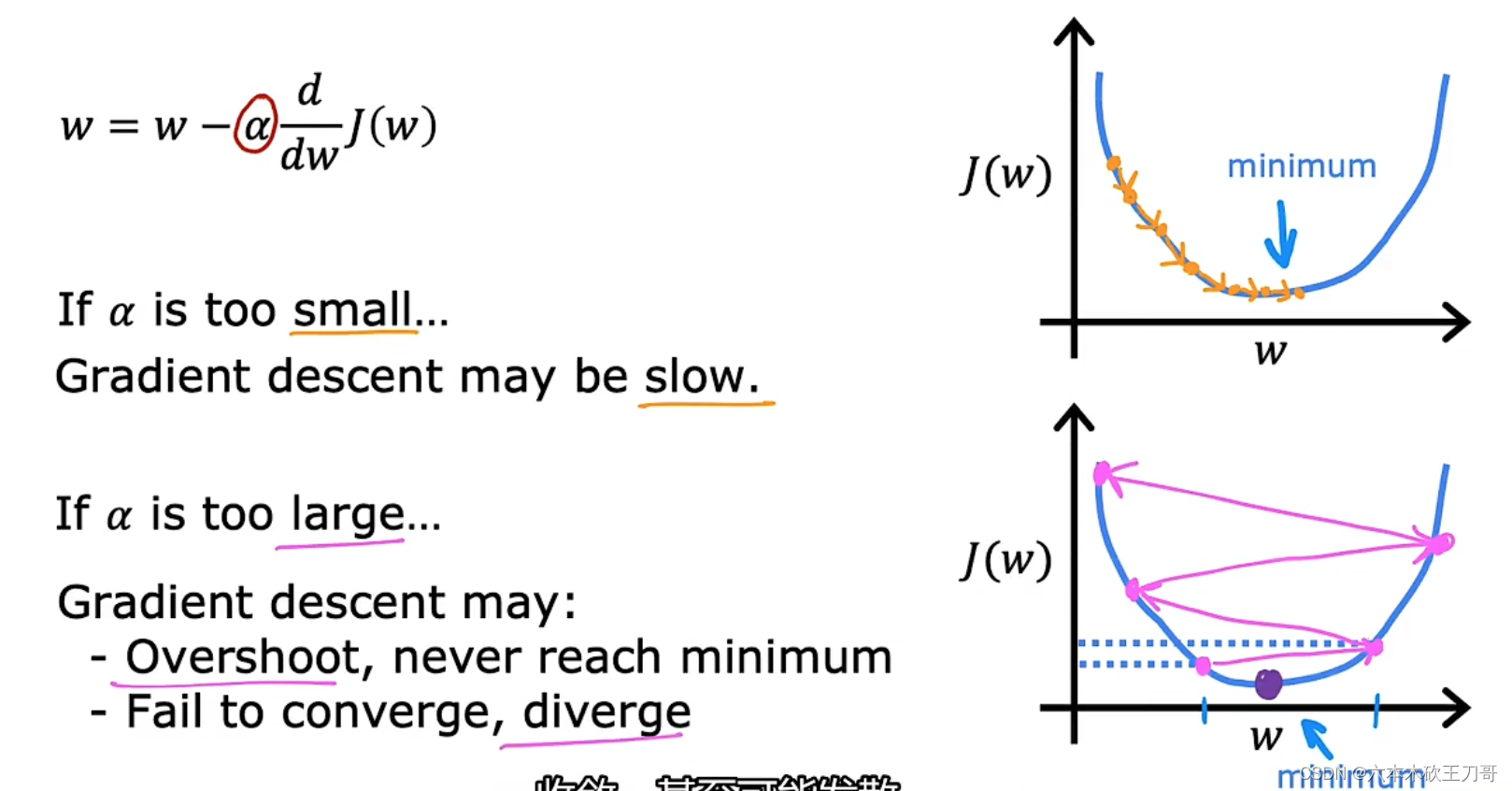
让我们来看看如果𝑎太小或𝑎太大会出现什么情况:
如果𝑎太小了,即我的学习速率太小,结果就是只能这样像小宝宝一样一点点地挪动, 去努力接近最低点,这样就需要很多步才能到达最低点,所以如果𝑎太小的话,可能会很慢, 因为它会一点点挪动,它会需要很多步才能到达全局最低点。
如果𝑎太大,那么梯度下降法可能会越过最低点,甚至可能无法收敛,下一次迭代又移动了一大步,越过一次,又越过一次,一次次越过最低点,直到你发现实际上离最低点越来越远,所以,如果𝑎太大,它会导致无法收敛,甚至发散。
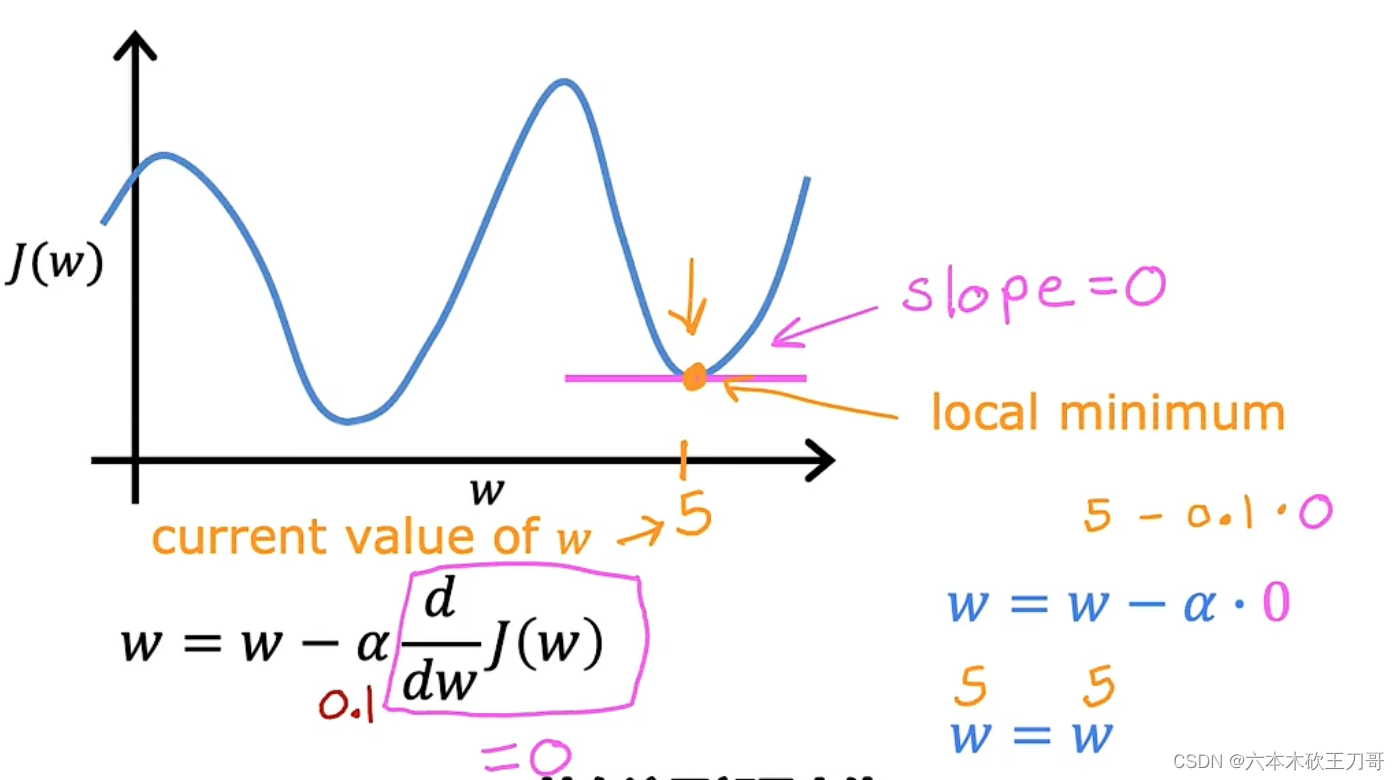
现在,还有一个问题,如果我们预先把w放在一个局部的最低点,你认为下一步梯度下降法会怎样工作? 假设你将w初始化在局部最低点,在这儿,它已经在一个局部的最优处或局部最低点。
结果是局部最优点的导数将等于零,因为它是那条切线的斜率。这意味着你已经在局部最优点,它使得w不再改变,也就是新的w等于原来的w,因此,如果你的参数已经处于局部最低点,那么梯度下降法更新其实什么都没做,它不会改变参数的值。这也解释了为什么即使学习速率𝑎保持不变时,梯度下降也可以收敛到局部最低点。
我们来看一个例子,我想找到它的最小值,首先初始化我的梯度下降算法,在那个品红色的点初始化,如果我更新一步梯度下降,也许它会带我到这个点,因为这个点的导数是相当陡的。现在,在这 个绿色的点,如果我再更新一步,你会发现我的导数,也即斜率,是没那么陡的。随着我接近最低点,我的导数越来越接近零,所以,梯度下降一步后,新的导数会变小一点点。然后我想再梯度下降一步,在这个绿点,我自然会用一个稍微跟刚才在那个品红点时比,再小一点的一步,到了新的红色点,更接近全局最低点了,因此这点的导数会比在绿点时更小。所以,我再进行一步梯度下降时,我的导数项是更小的,w更新的幅度就会更小。所以随着梯度下降法的运行,你移动的幅度会自动变得越来越小,直到最终移动幅度非常小,你会发现已经收敛到局部极小值。
回顾一下,在梯度下降法中,当我们接近局部最低点时,梯度下降法会自动采取更小的 幅度,这是因为当我们接近局部最低点时,很显然在局部最低时导数等于零,所以当我们接近局部最低时,导数值会自动变得越来越小,所以梯度下降将自动采取较小的幅度,这就是梯度下降的做法。所以实际上没有必要再另外减小𝑎。
2.3.4 梯度下降的线性回归
三、numpy的向量Vectors、矩阵Matrices
四、多元线性回归 multiple linear regression
4.1 多维特征
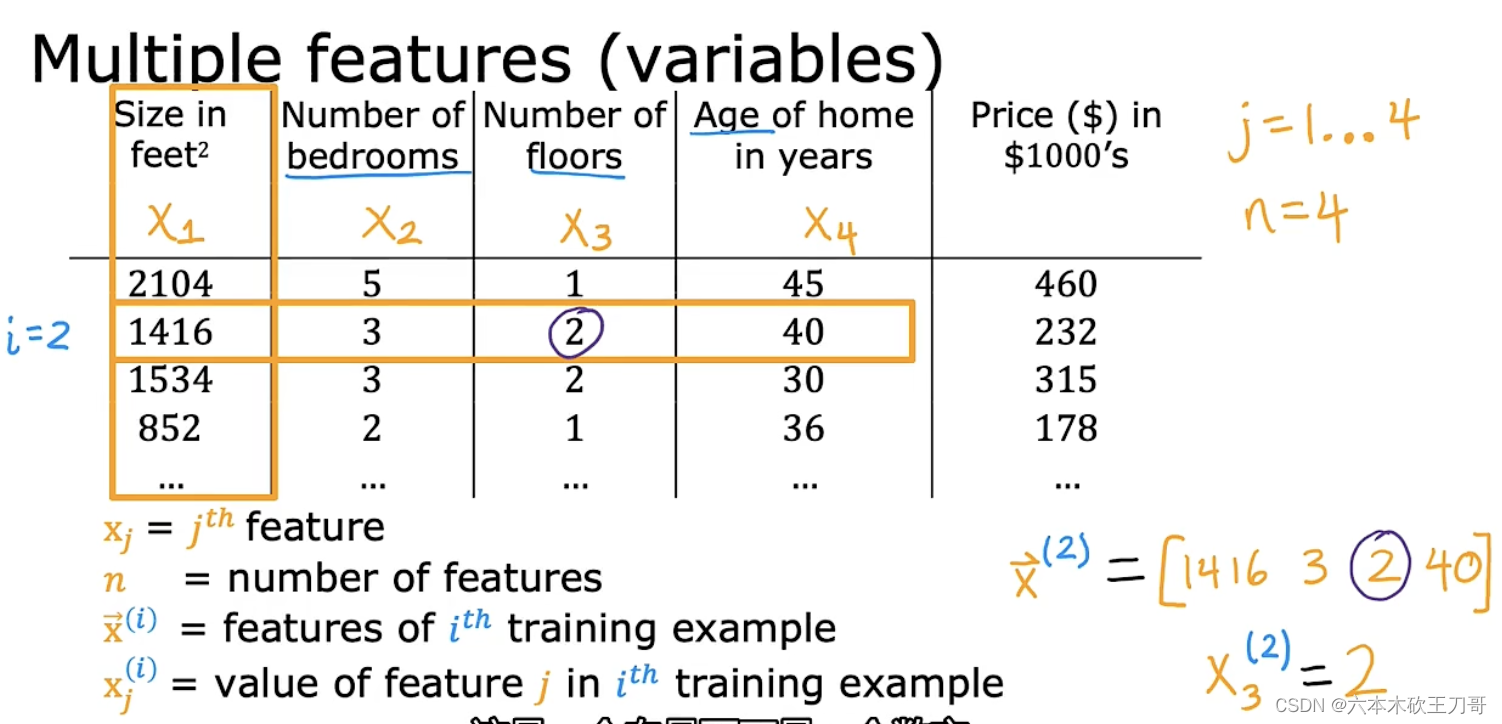
目前为止,我们探讨了单变量/特征的回归模型,现在我们对房价模型增加更多的特征, 例如房间数楼层等,构成一个含有多个变量的模型,模型中的特征为(𝑥1, 𝑥1, . . . , 𝑥𝑛)。
增添更多特征后,我们引入一系列新的注释:
𝑛 代表特征的数量
𝑥(𝑖)代表第 𝑖 个训练实例,是特征矩阵中的第𝑖行,是一个向量(vector)。
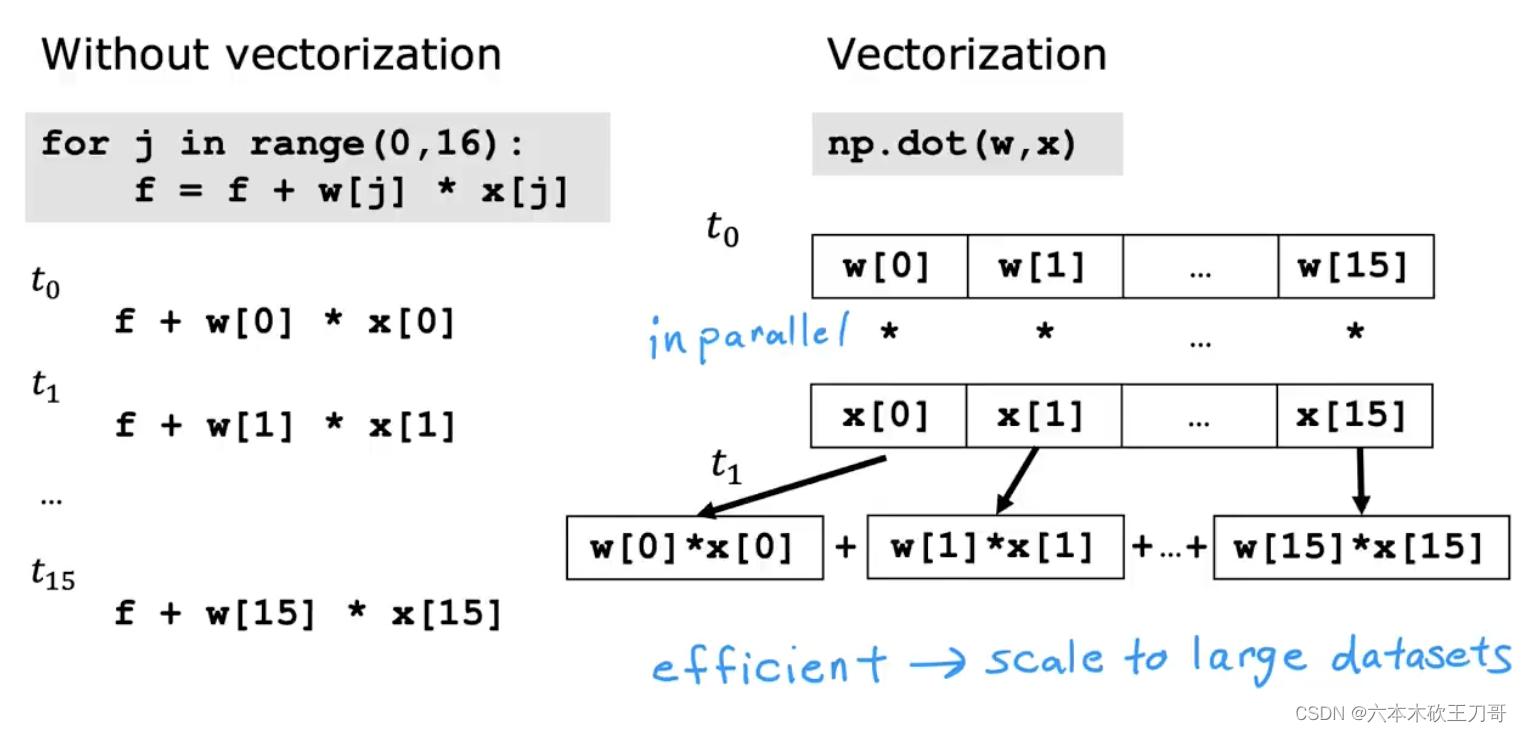
4.2向量化
使用NumPy向量化提高计算性能,充分利用CPU或者GPU的并行性。
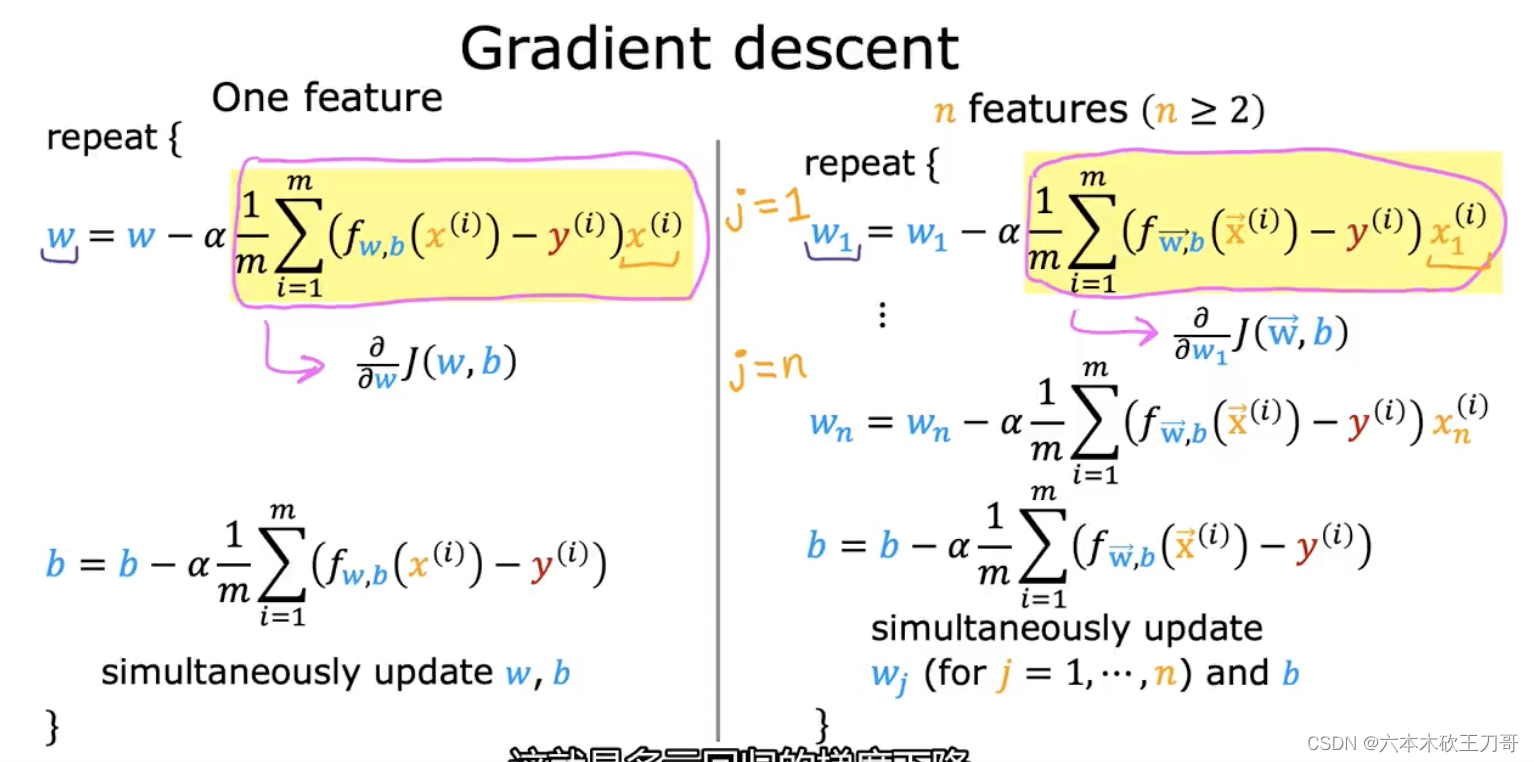
4.3多元梯度下降法 Gradient Descent With Multiple Variables
在原来的多元表示中,我们使用多个变量,但是在向量表示中,可以使用向量来替代。
与单变量线性回归类似,在多变量线性回归中,我们也构建一个代价函数,则这个代价函数是所有建模误差的平方和,我们的目标和单变量线性回归问题中一样,是要找出使得代价函数最小的一系列参数。 多变量线性回归的批量梯度下降算法为:
另一种方法是normal equation,但是用的不多。
4.4 特征缩放
-
目的 :让梯度下降运行的更快
-
问题:当特征范围相差太大时,会一直来回振荡,梯度下降效率低。
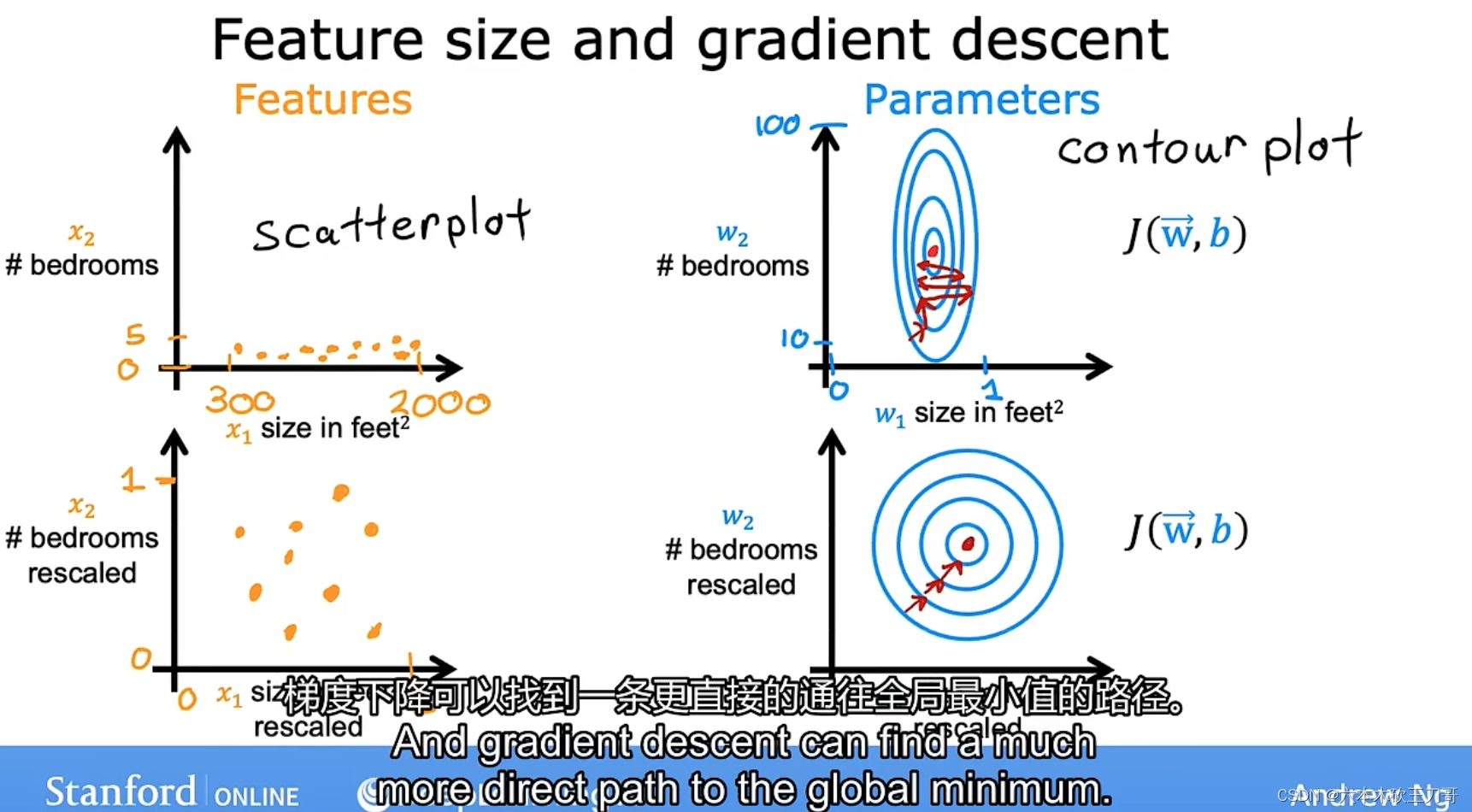
在我们面对多维特征问题的时候,我们要保证这些特征都具有相近的尺度,这将帮助梯度下降算法更快地收敛。
以房价问题为例,假设我们使用两个特征,房屋的尺寸和房间的数量,尺寸的值为 0- 2000 平方英尺,而房间数量的值则是 0-5,以两个参数分别为横纵坐标,绘制代价函数的等高线图能,看出图像会显得很扁,梯度下降算法需要非常多次的迭代才能收敛。
解决的方法是尝试将所有特征的尺度都尽量缩放到-1 到 1 之间。
其中一种缩放方法如下图:
4.4.1 均值归一化 Mean normalization
数据只有正值,经过均值归一化,数据既有正数又有负数。
其中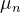
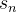
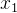
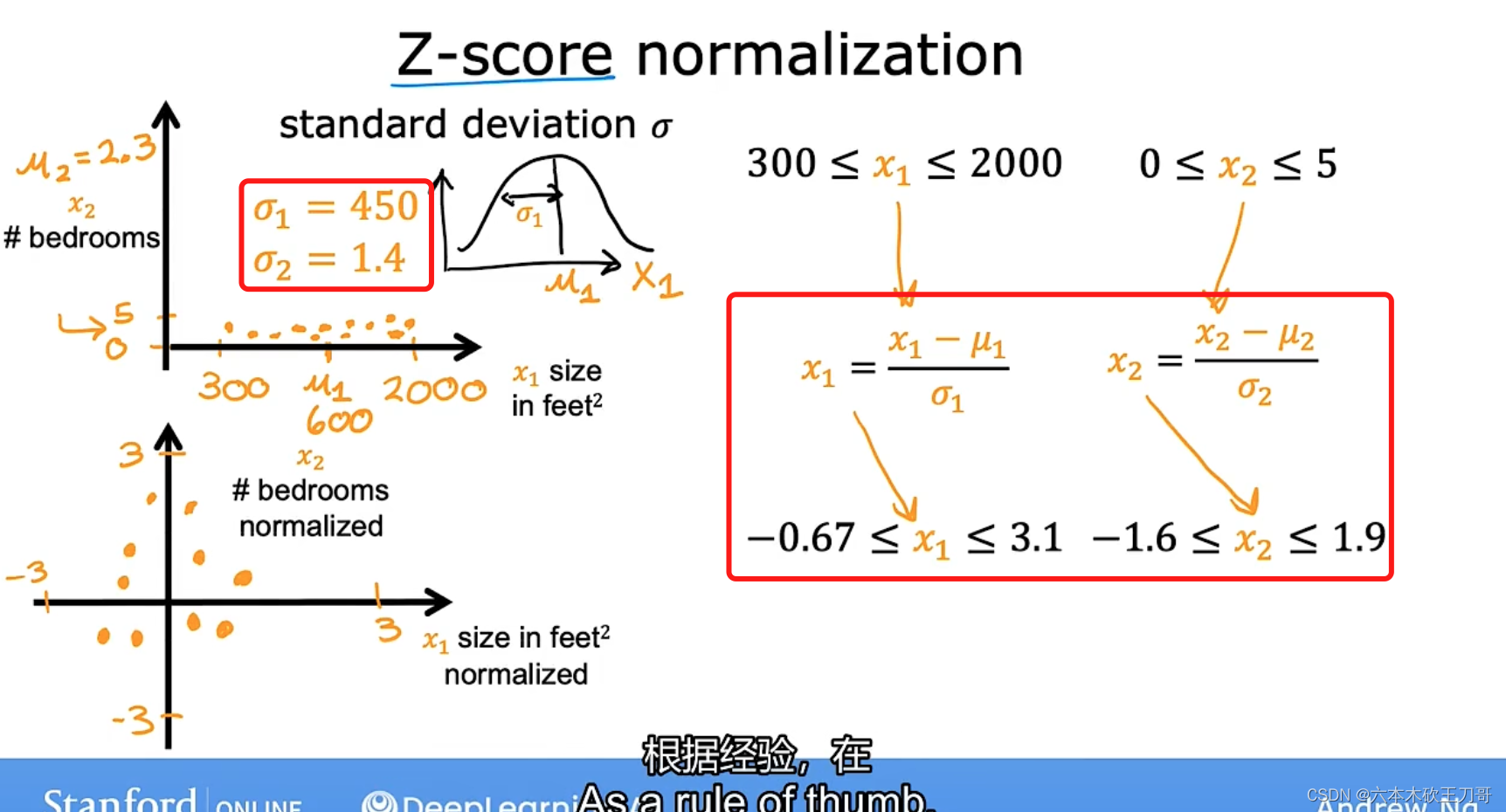
4.4.2 Z-score normalization Z-score归一化
第二种归一化方法,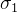
根据情况推荐是否缩放
4.5 判断收敛和学习率
在以下的多元线性回归梯度下降法中,选择Alpha是很重要的。
4.5.1 判断梯度下降是否收敛的方法和学习曲线 learning curve
在下图中,横坐标代表迭代的次数,每次迭代会同步更新w向量和b。这和之前的单变量线性回归的横坐标是w不一样。这条曲线也可以称之为学习曲线。
例如图中的100次迭代和200次迭代,它的代价函数的J值都下降了,如果J值不下降,这意味着学习率的选择出现了问题。然后在300次迭代,曲线变的平坦,第400次迭代的时候,曲线已经收敛,所以是经过一定次数迭代之后,J收敛到小于某个值,从而变得平坦。根据应用程序的不同,收敛所需要的迭代次数不同。
第二种方法是自动测试代价函数是否收敛,例如将代价函数的变化值与某个阀值(例如 0.001) 进行比较,当小于这个阈值的时候,说明收敛。
梯度下降算法收敛所需要的迭代次数根据模型的不同而不同,我们不能提前预知,我们可以绘制迭代次数和代价函数的图表来观测算法在何时趋于收敛。
4.5.2 学习率的选择
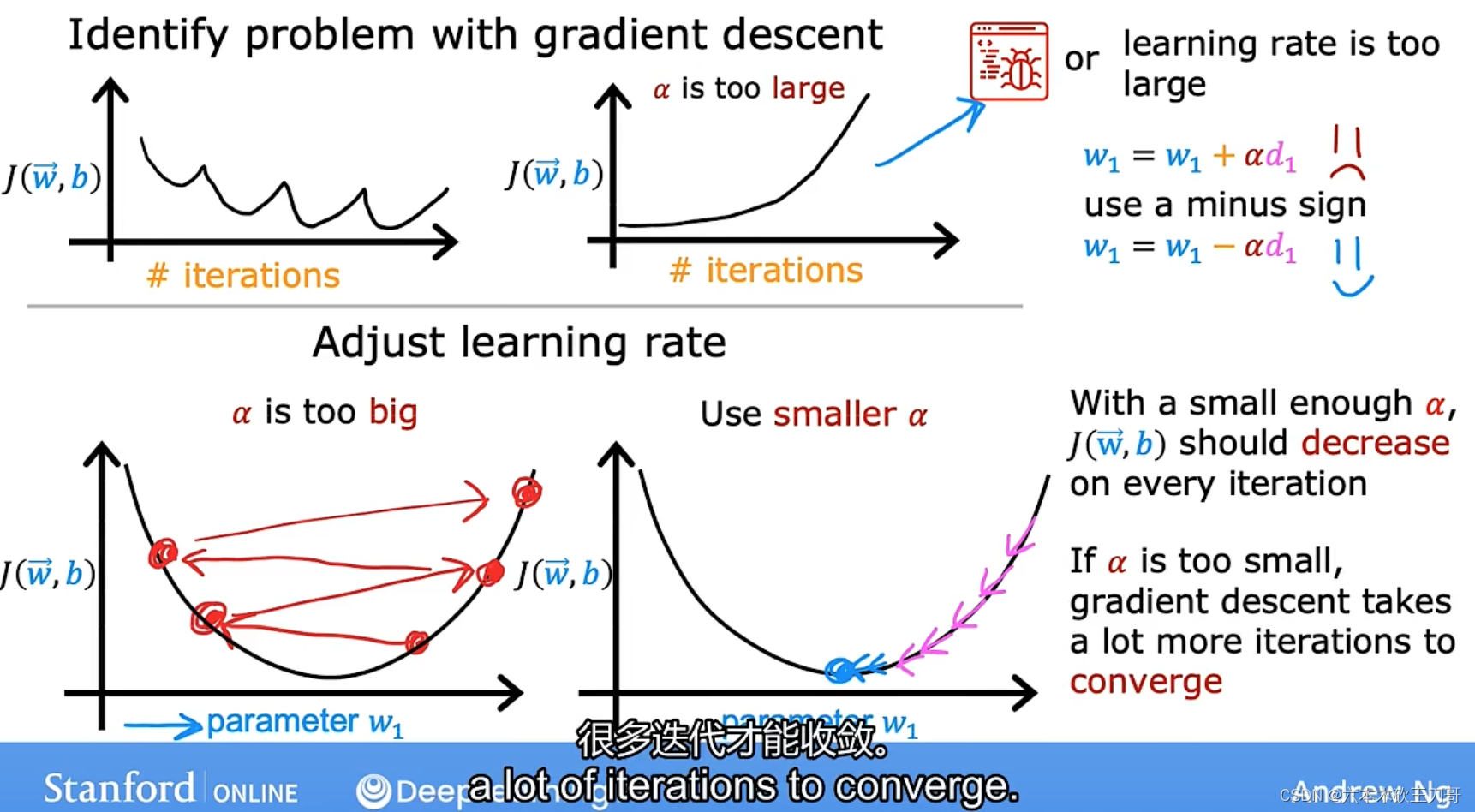
梯度下降算法的每次迭代受到学习率的影响,如果学习率𝑎过小,则达到收敛所需的迭代次数会非常高;如果学习率𝑎过大,每次迭代可能不会减小代价函数,可能会越过局部最小值导致无法收敛。
当然除了这个学习率选择问题也有代码的bug问题,例如在更新w的时候,使用了加号+,加上学习率乘导数会导致w变大,可能会导致无法收敛。
通常可以考虑尝试些学习率: 0.01,0.03,0.1,0.3,1,3,10
4.6 特征和多项式回归 polynomial regression
4.6.1 特征工程 feature engineering
通过转换、结合设计新的特征x
假设有两个特征:x1 是土地宽度,x2 是土地纵向深度。
由于房价实际与面积挂钩,所以提取出新特征:面积x3 = x1 * x2,以获得更好的模型。
4.6.2 多项式回归
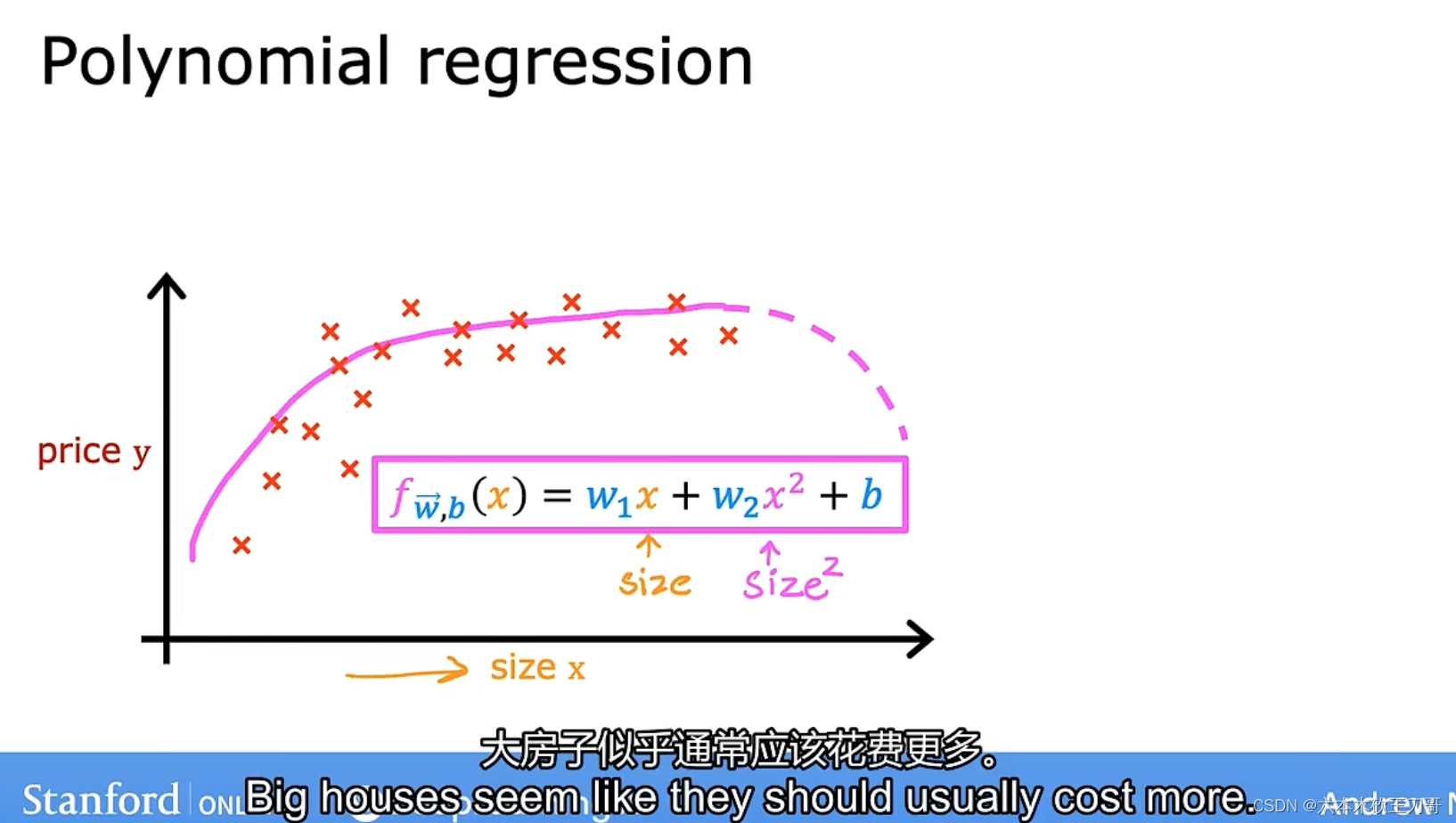
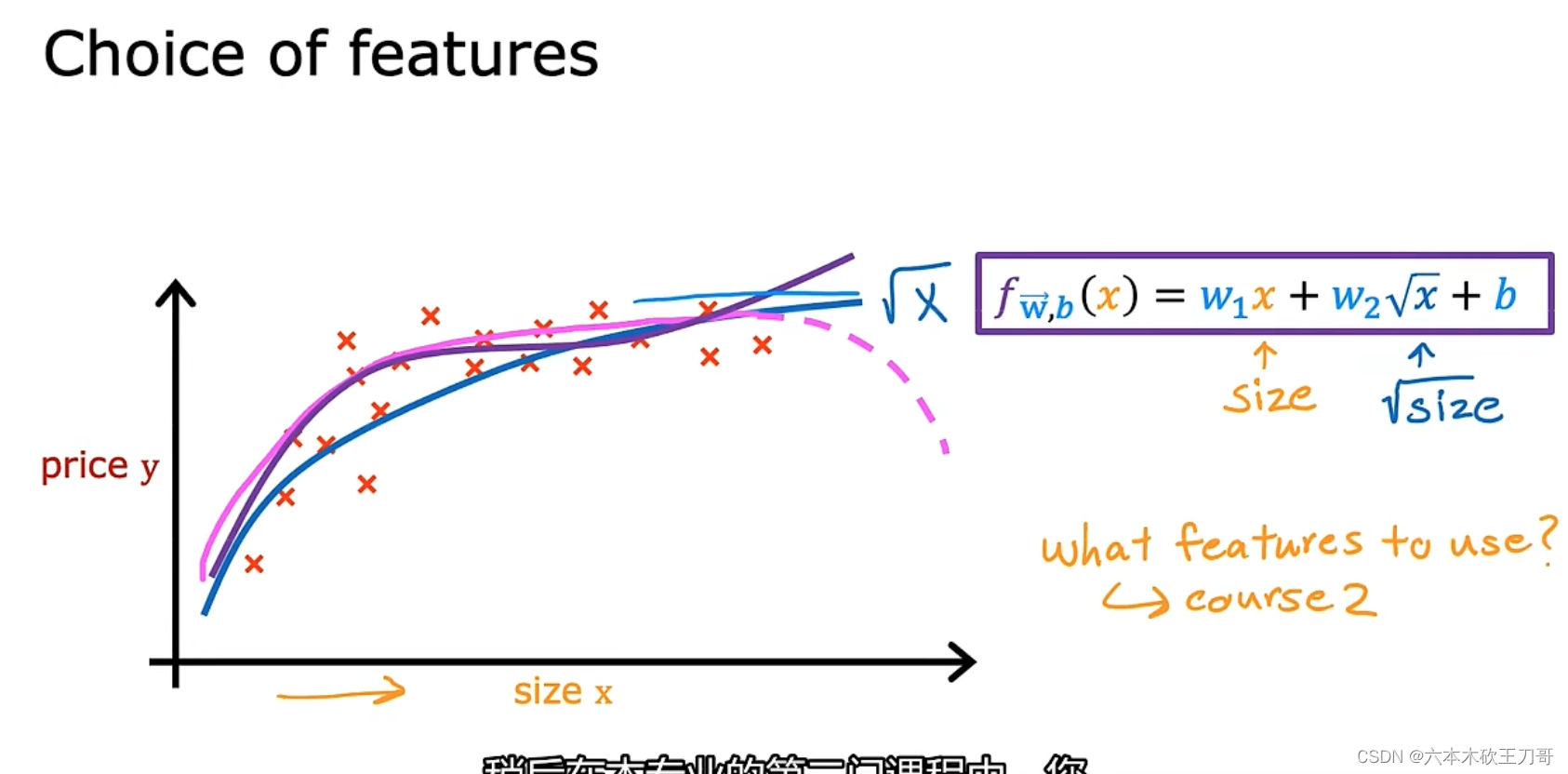
线性回归并不适用于所有数据,有时我们需要曲线来适应我们的数据,比如一个二次方模型。
但是下图中的二次曲线后半的price下降,明显不符合实际。(房价不会随着size变大而变低)
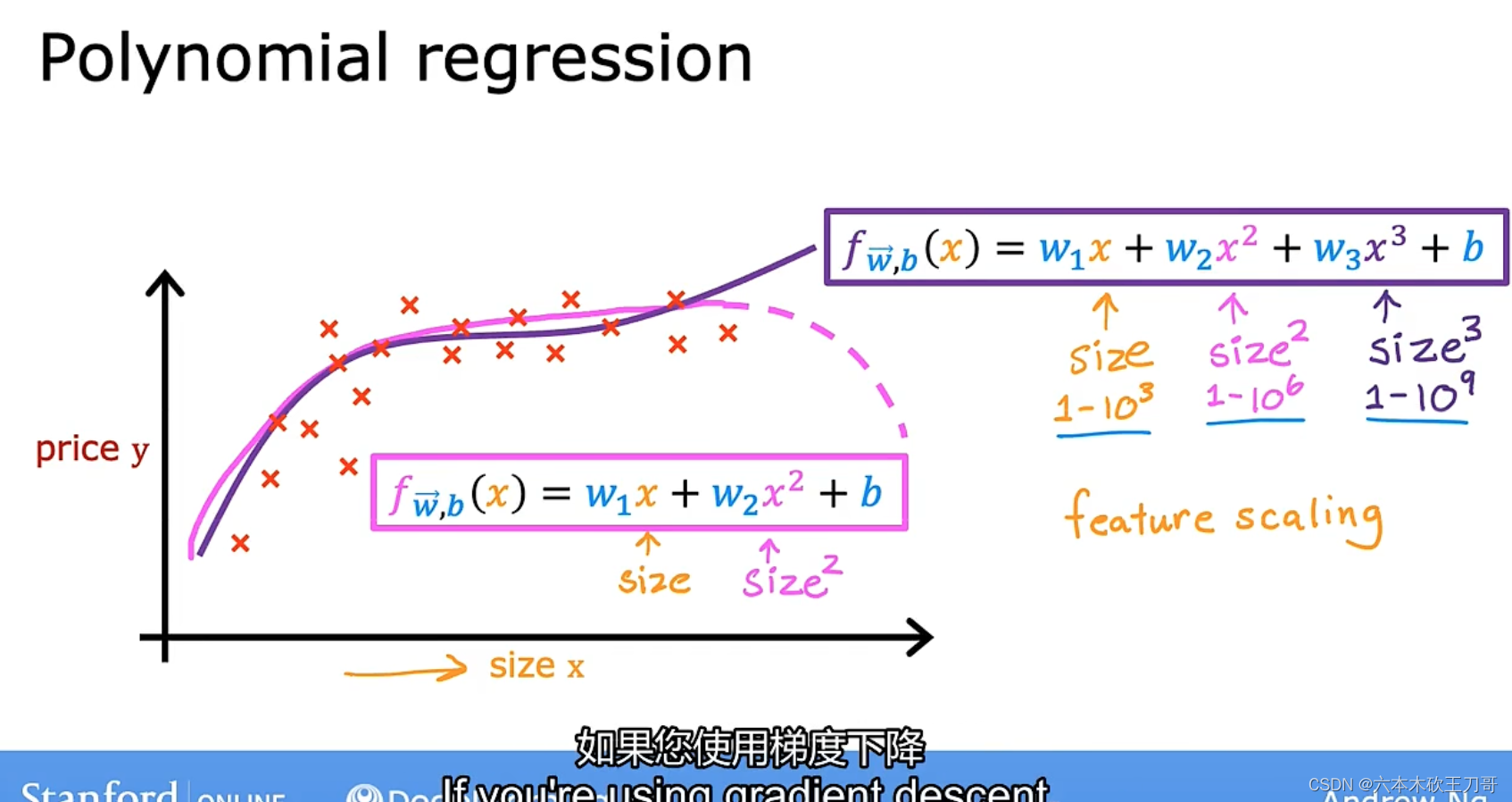
可以选用三次模型进行拟合。
曲线符合实际,但由于二次方和三次方的出现,特征缩放将会变得很重要,要十分注意自变量范围的选取。
特征被重新标定,特征缩放,让它们彼此之间具有可比性,例如当初始size选取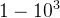
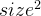
选用根号模型
能充分拟合,且自变量范围可变曲度大(形状变化)
五、逻辑回归logistic regression——分类问题
5.1 线性回归对于分类问题的局限性和逻辑回归
在分类问题中,你要预测的变量 𝑦 是离散的值,我们将学习一种叫做逻辑回归 (Logistic Regression) 的算法,这是目前最流行使用最广泛的一种学习算法。
在分类问题中,我们尝试预测的是结果是否属于某一个类(例如正确或错误)。分类问 题的例子有:判断一封电子邮件是否是垃圾邮件;判断一次金融交易是否是欺诈;之前我们 也谈到了肿瘤分类问题的例子,区别一个肿瘤是恶性的还是良性的。
我们从二元的分类问题开始讨论。
我们将因变量(dependent variable)可能属于的两个类分别称为负向类(negative class)和正向类(positive class), 0 表示负向类,1 表示正向类。
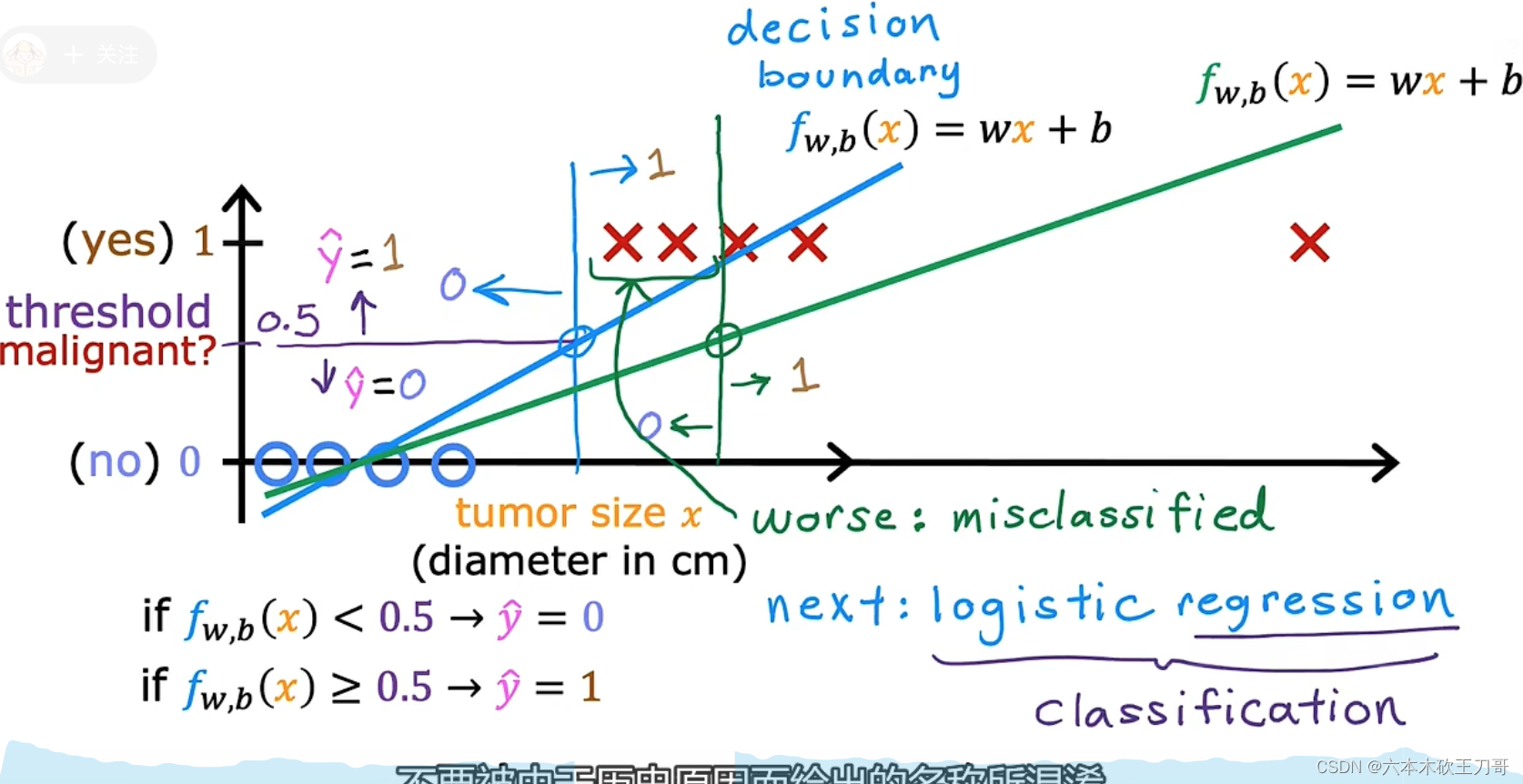
对于没有离群点的数据,一个线性模型似乎能很好地完成分类任务。假使我们又观测到一个非常大尺寸的恶性肿瘤,将其作为实例加入到我们的训练集中来,这将使得我们获 得一条新的直线。
由于离群点的存在,线性回归不适用于分类问题。如下图(阈值为0.5),由于最右离群点,再用线性回归与实际情况不拟合。
如果我们要用线性回归算法来解决一个分类问题,对于分类, 𝑦 取值为 0 或者 1,但如果你使用的是线性回归,那么假设函数的输出值可能远大于 1,或者远小于 0,即使所有训练样本的标签 𝑦 都等于 0 或 1。尽管我们知道标签应该取值 0 或者 1,但是如果算法得到的值远大于 1 或者远小于 0 的话,就会感觉很奇怪。所以我们在接下来的要研究的算法就叫做逻辑回归算法,这个算法的性质是:它的输出值永远在 0 到 1 之间。
顺便说一下,逻辑回归算法是分类算法,我们将它作为分类算法使用。有时候可能因为 这个算法的名字中出现了“回归”使你感到困惑,但逻辑回归算法实际上是一种分类算法,它适用于标签 𝑦 取值离散的情况,如:1 0 0 1。
引入逻辑回归(logistic regression)算法,来解决这个问题,其实是Sigmoid公式。下图中的sigmoid函数g(z),无论z取多大或者多小, g(z)的值永远都在0和1之间。
更进一步,如果我们把之前的线性回归函数表达式wx+b代入z,得到关于x的新的表达式f(x) = g(wx+b),这样就可以把输出限制到了0到1之间。
下面来看一下这个函数的相关解释,如果给出肿瘤大小x,此时输出的值为0.7,说明此时肿瘤恶性的概率为70%,为了保证结果只为1或者0,我们认为肿瘤良性的概率为0.3,此时两个概率相加为1,在一些不同的数学表示上,用条件概率来表示这个概念,当给出x以及w和b基础上,得到y=1的概率。
5.2 决策边界 decision boundary
现在讲下决策边界(decision boundary)的概念。这个概念能更好地帮助我们理解逻辑回归的假设函数在计算什么。
在预测中,需要假设在什么情况下预测的概率为1或者为0,这就是决策边界的问题。
推导什么情况下是分界线,sigmoid函数中,当z为0的时候,取值正好是0.5,所以可以把z>=0和z<0作为判断的标准,z对应wx+b。
案例1:
下列的分类问题中,如何划分y=0和y=1的情况,引入之前的g(z),z大于0和小于0的时候分别预测为0和1,所以此时要找到z=0的那条线,在这种情况下,有两个特征x1和x2,让w1和w2都为1,b为3,此时决策边界是下图的一条直线。当然如果选用不同的参数值,那么决策边界也可以是别的直线。
案例二:
遇到下图的分类问题,需要用多项式特征(使用多项式也是线性回归的一种),此时决策边界是一个圆。
案例三:
可以根据情况选择不同的非线性边界,多项式可以拟合更复杂的情形。
5.3 逻辑回归的代价函数 cost function
我们要介绍如何拟合逻辑回归模型的参数w。具体来说,要定义用来拟合参数的优化目标或者叫代价函数,这便是监督学习问题中的逻辑回归模型的拟合问题。
5.3.1 loss function
如下的训练集合,如何选择w和b?
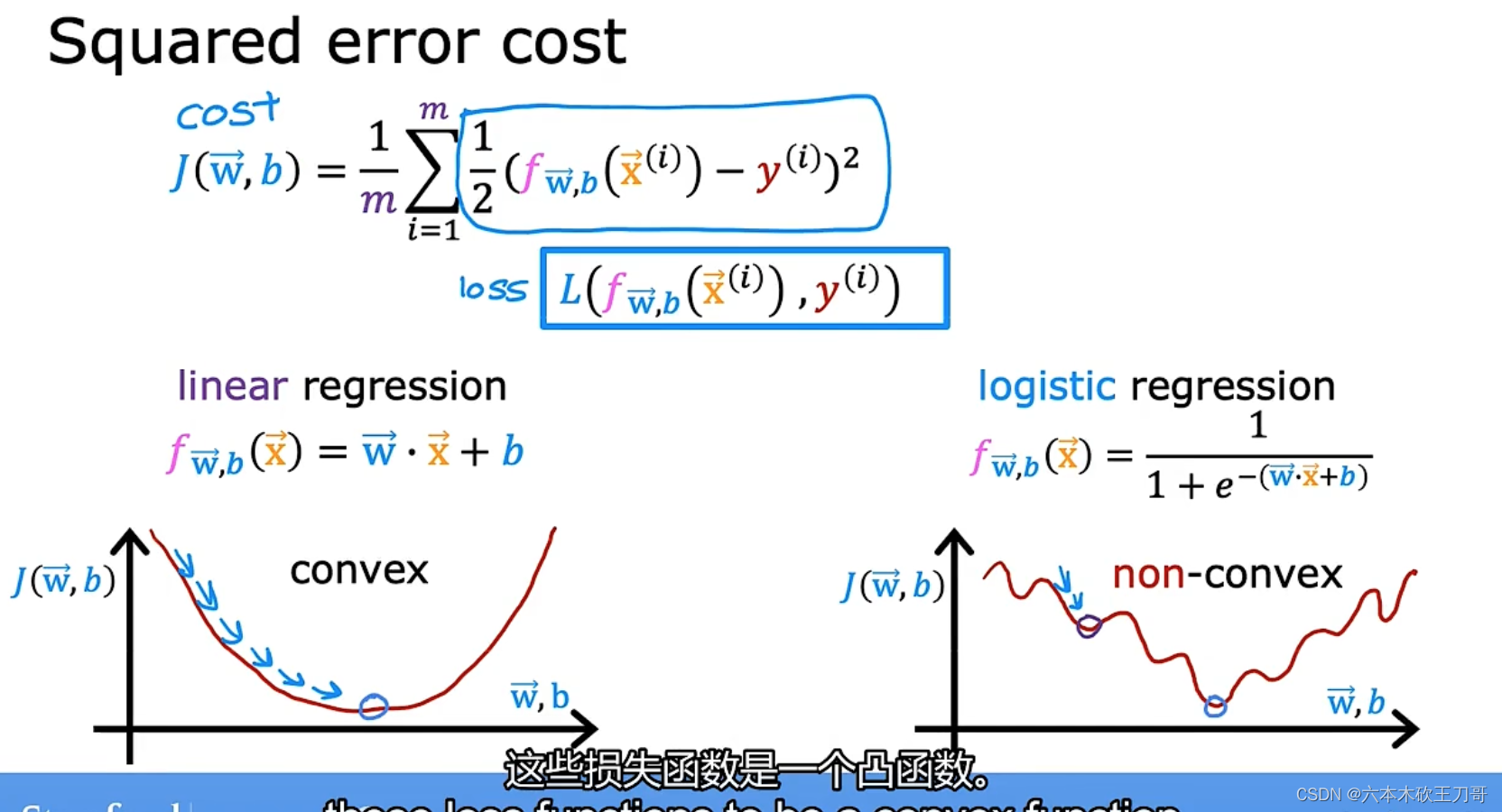
对于线性回归模型,我们定义的代价函数是所有模型误差的平方和。理论上来说,我们也可以对逻辑回归模型沿用这个定义,但是问题在于,当我们将Sigmoid函数带入到定义的代价函数中时,我们得到的代价函数将是一个非凸函数(non-convexfunction)。这意味着我们的代价函数有许多局部最小值,这将影响梯度下降算法寻找全局最小值。
将线性回归的代价函数改写为蓝框内的形式 (即把1/2提到后面去),得到逻辑回归的cost function。
上图蓝框的损失函数 loss function 是在一个训练样本的表现,把所有训练样本的损失加起来得到的代价函数 cost function,才能衡量模型在整个训练集上的表现
5.3.2 逻辑回归的loss函数和cost函数
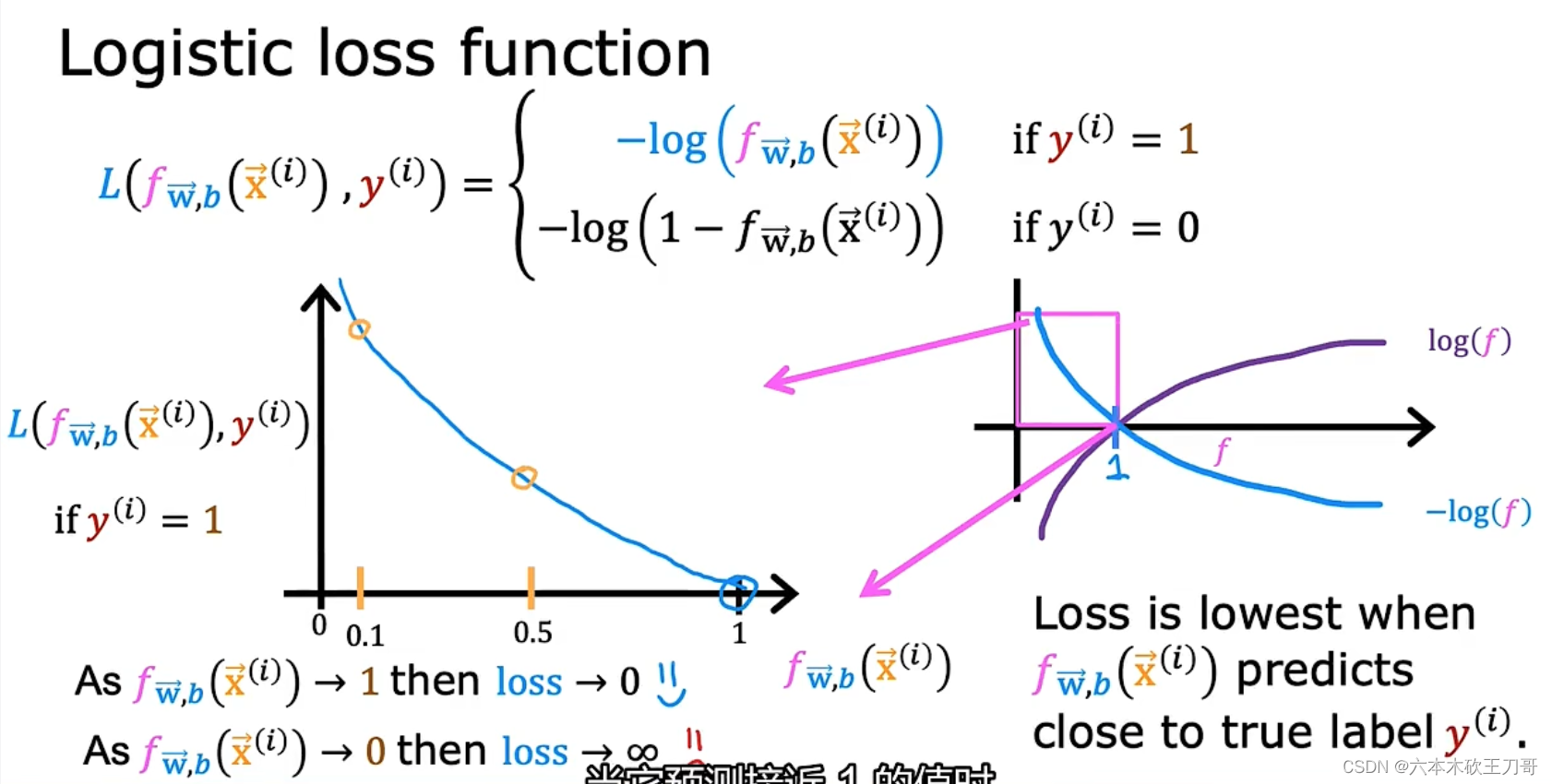
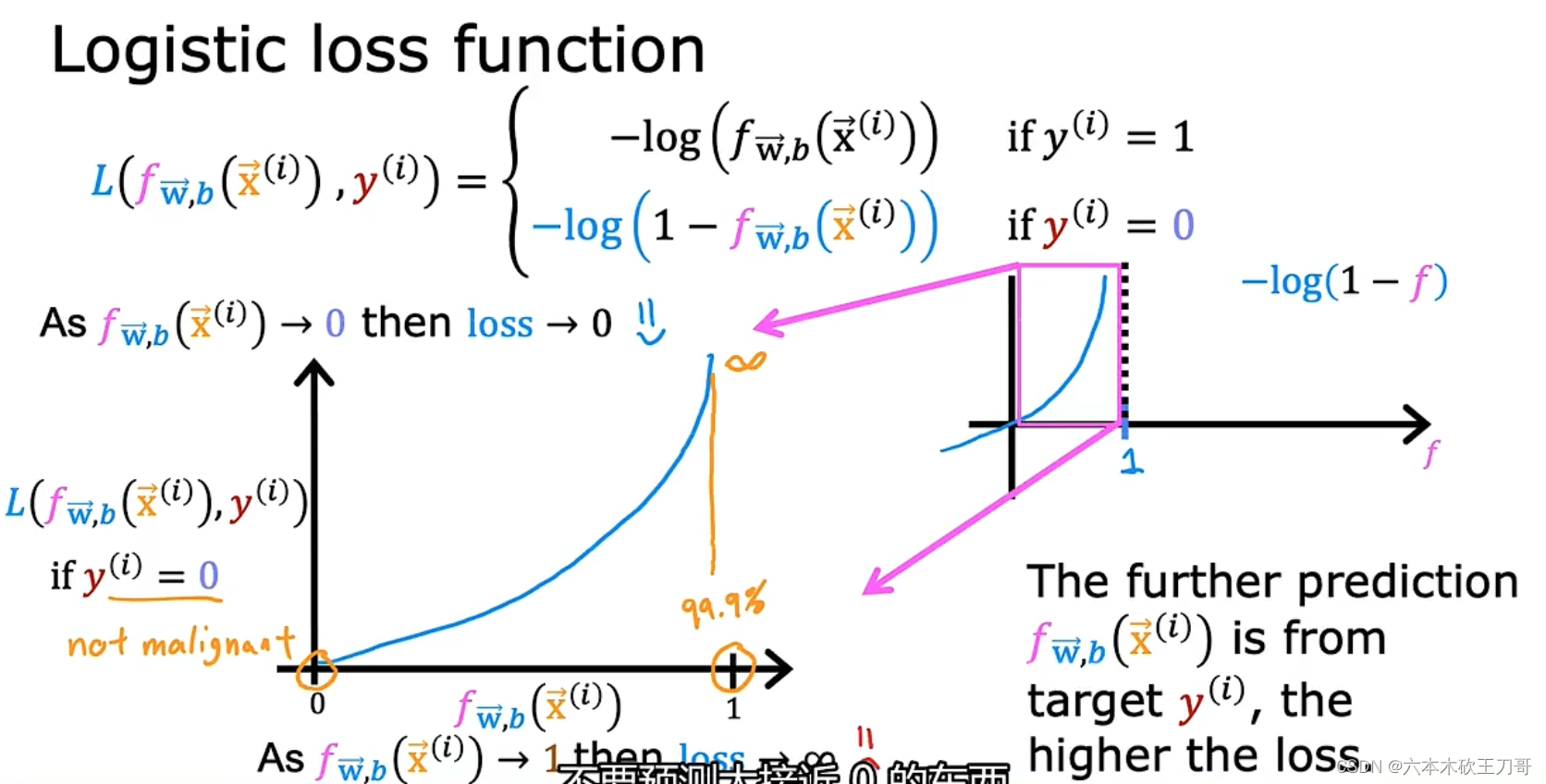
我们把逻辑回归的损失函数定义为两种对数函数。
首先研究第一个对数函数,预测y=1时的损失函数。因为逻辑回归函数fw, b(x)的输出总是在0和1之间(因为f(x)其实是g(z),它的函数形式是一个Sigmoid函数,限制了f(x)输出在0到1之之间),所以可以画出损失函数f取值是0到1之间的一部分图像。(如下左图所示,把横坐标0到1间的函数图像拿出来)
观察左图,当f输出是0.5的时候,图像的取值不是很大,但是当f是0.1的时候,图像的输出非常大,也就是损失函数的值很大,也就是说这个损失函数保证了当预测值是1的时候,损失是最小的。记住我们训练的目的是让损失函数最小,如果这个损失函数较大的话,模型就大概率不会把它预测为1。
在下图假设在y预测为0的时候,如果此时说99.9%的可能性是恶性肿瘤,但是在这个代价函数中,x趋于0.99的惩罚代价是非常大的(very high loss)。
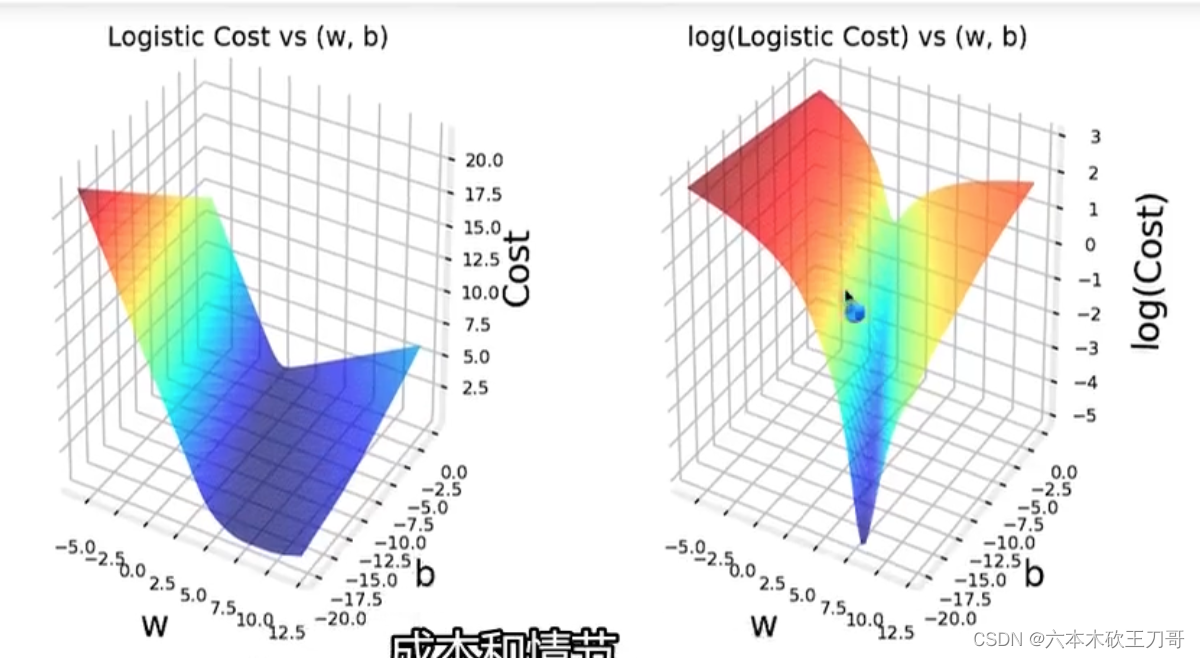
我们定义了单训练样本的代价函数,凸性分析的内容是超出这门课的范围的,但是可以证明我们所选的代价函数会给我们一个凸优化问题。代价函数𝐽(w,b)会是一个凸函数,并且没有局部最优值。(下图就是这个凸函数三维图像,它没有局部最小值)
5.3.3 简化逻辑回归cost函数和梯度下降实现
找出一种稍微简单一点的方法来写代价函数,来替换我们现在用的方法,把分类讨论巧妙利用条件合并为一个式子。同时我们还要弄清楚如何运用梯度下降法,来拟合出逻辑回归的参数。因此,之后就应该知道如何实现一个完整的逻辑回归算法。
下图展示了简化后的损失函数 loss function,当y取0或者1的时候,得到的函数值和之前一样。
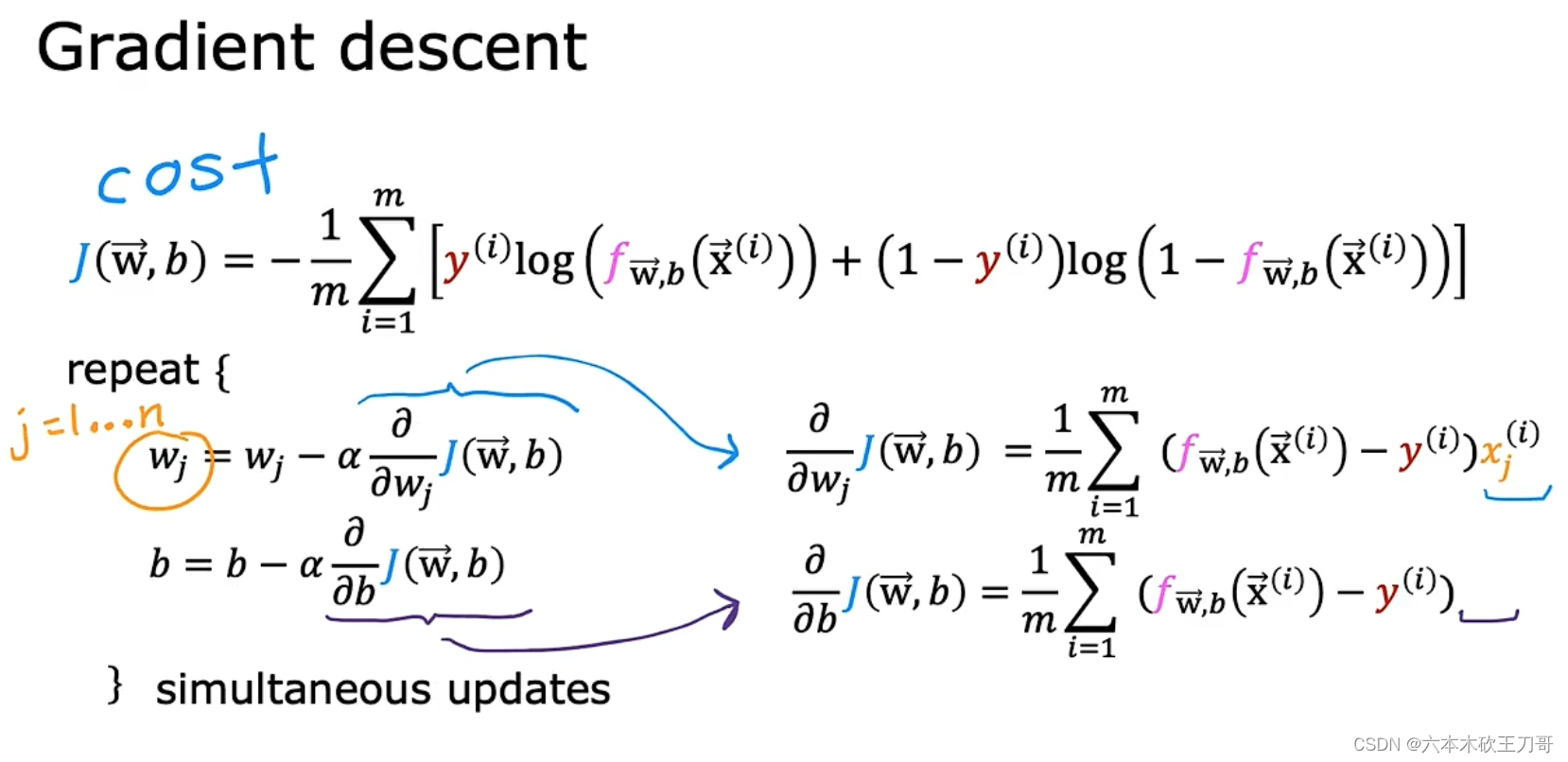
结合了以上损失函数,我们把它代入到代价函数cost function中,为什么获得这个结果呢?因为推导自最大似然估计,但是并不需要理解它,这只是这个代价函数背后的深层次的数学知识。
接下来讨论最小化以上代价函数的方法,是使用梯度下降法(gradient descent)。
为了拟合出逻辑回归的模型,需要找出最佳的w和b让代价函数J的值最小。
当然,求解偏导数的规则需要解决函数求导的知识,包括Sigmoid函数和对数函数求导,针对损失函数J对w求导的过程,可以参考:逻辑回归的梯度下降公式详细推导过程_逻辑回归梯度下降推导_iioSnail的博客-CSDN博客
有时间尽量补充出自己手动求导的过程。(留白)
现在,如果把这个更新规则和我们之前用在线性回归上的进行比较的话,我们会惊讶地发现,这个式子正是我们用来做线性回归梯度下降的。(本质上的推导过程肯定是不一样的,只是推导出的最终结果恰好一样)
那么,线性回归和逻辑回归是同一个算法吗?要回答这个问题,我们要观察逻辑回归看看发生了哪些变化。实际上,假设的定义发生了变化。
逻辑回归的梯度下降看似与线性回归的梯度下降相同,但本质不同,因为他们的fx的原型不一样。
因此,即使更新参数的规则看起来基本相同,但由于假设的定义发生了变化,所以逻辑函数的梯度下降,跟线性回归的梯度下降实际上是两个完全不同的东西。
在先前的视频中,当我们在谈论线性回归的梯度下降法时,我们谈到了如何监控梯度下降法以确保其收敛,我通常也把同样的方法用在逻辑回归中,来监测梯度下降,以确保它正常收敛。
当使用梯度下降法来实现逻辑回归时,我们有这些不同的参数w,就是w0 w1 w2 一直到 w𝑛,我们需要用这个表达式来更新这些参数。我们还可以使用 for 循环来更新这些参数值, 用 for i=1 to n,或者 for i=1 to n+1。当然,不用 for 循环也是可以的,理想情况下,我们更提倡使用向量化的实现,可以把所有这些 n 个参数同时更新。
最后还有一点,我们之前在谈线性回归时讲到的特征缩放,我们看到了特征缩放是如何 提高梯度下降的收敛速度的,这个特征缩放的方法,也适用于逻辑回归。如果你的特征范围差距很大的话,那么应用特征缩放的方法,同样也可以让逻辑回归中,梯度下降收敛更快。
就是这样,现在你知道如何实现逻辑回归,这是一种非常强大,甚至可能世界上使用最广泛的一种分类算法。
六、过拟合问题
6.1 过拟合定义
过拟合:当变量过多时,训练出来的假设能很好地拟合训练集,所以代价函数实际上可能非常接近于0,但得到的曲线为了千方百计的拟合数据集,导致它无法泛化到新的样本中,无法预测新样本数据
泛化:指一个假设模型应用到新样本的能力
6.1.1 过拟合案例
如果我们有非常多的特征,我们通过学习得到的假设可能能够非常好地适应训练集(代价函数可能几乎为 0),但是可能会不能推广到新的数据。
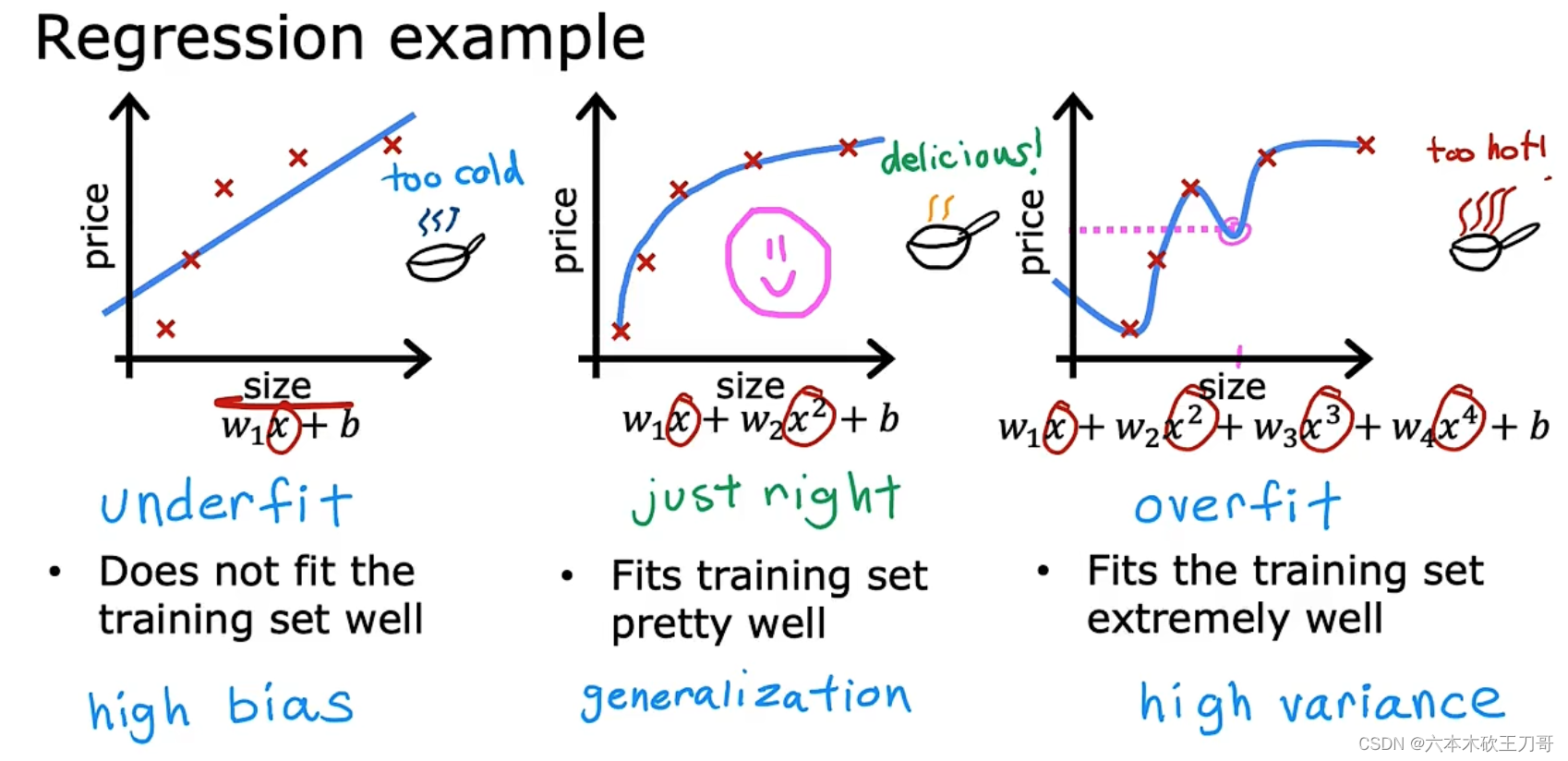
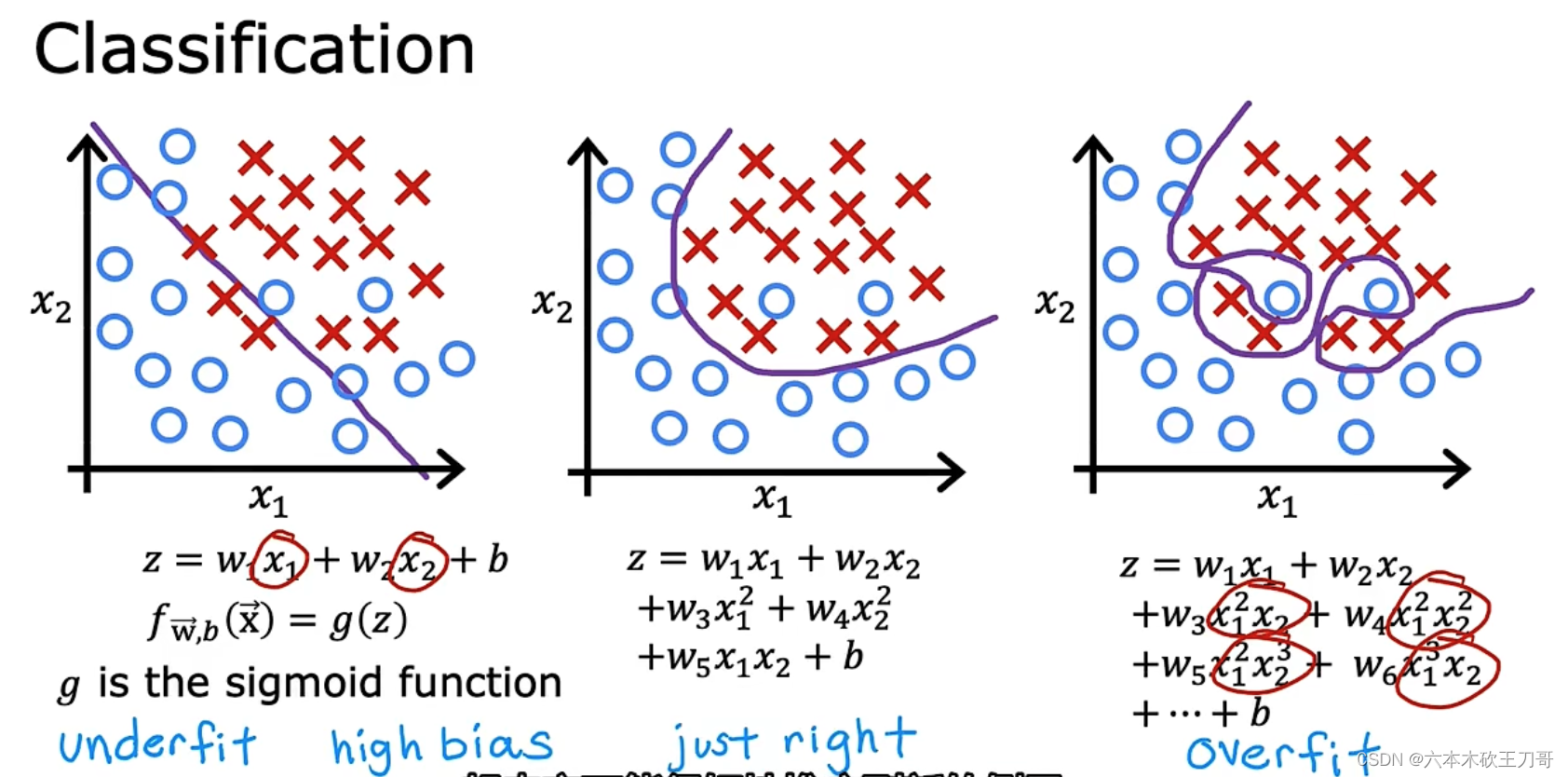
下面的例子中,第一个模型是一个线性模型,欠拟合 high bias,不能很好地适应我们的训练集,它以一次方程一种很强的preconception来拟合数据,或者说是有很强的bias认为这个房价预测问题将以一次直线来拟合;
第三模型是一个四次方的模型 high variance,过于强调拟合原始数据,而丢失了算法的本质:预测新数据。我们可以看出,若给出一个新的值使之预测,它将表现的很差,是过拟合,虽然能非常好地适应我们的训练集但在新输入变量进行预测时可能会效果不好;
而中间的模型似乎最合适,称为泛化 generalization。
分类问题也存在过拟合和欠拟合问题:
根据决策边界z=0,画出每一条分割线。就以多项式理解,𝑥 的次数越高,拟合的越好,但相应的预测的能力就可能变差。
6.1.2 解决过拟合方法
问题是,如果我们发现了过拟合问题,应该如何处理?
- 得到更多的数据
- 特征选择——选用特征的一部分
- 正则化——减少参数大小
第一种方法是获得更多的数据,但是这并不一定总是有效的,有时候并没有那么多的数据。
第二种方法是减少特征的选择,如果使用全部特征(此时可能会用高阶多项式来拟合)再加上不足够的数据,就可能会出现过拟合。如果选择部分最符合的特征,会带来不错的效果。但是但大部分特征都比较重要的时候,就会导致一些重要特征被丢弃。
第三种方法是正则化,前面的抛弃某些重要特征(把参数w设置为0)可能会带来不好的影响,所以我们可以把这个特征的参数尽可能减少以防止对模型有过大的影响,例如把w参数设置为0.0001.
以下总结了这三种方法:
6.2 过拟合的代价函数(正则化原理 Regularization)
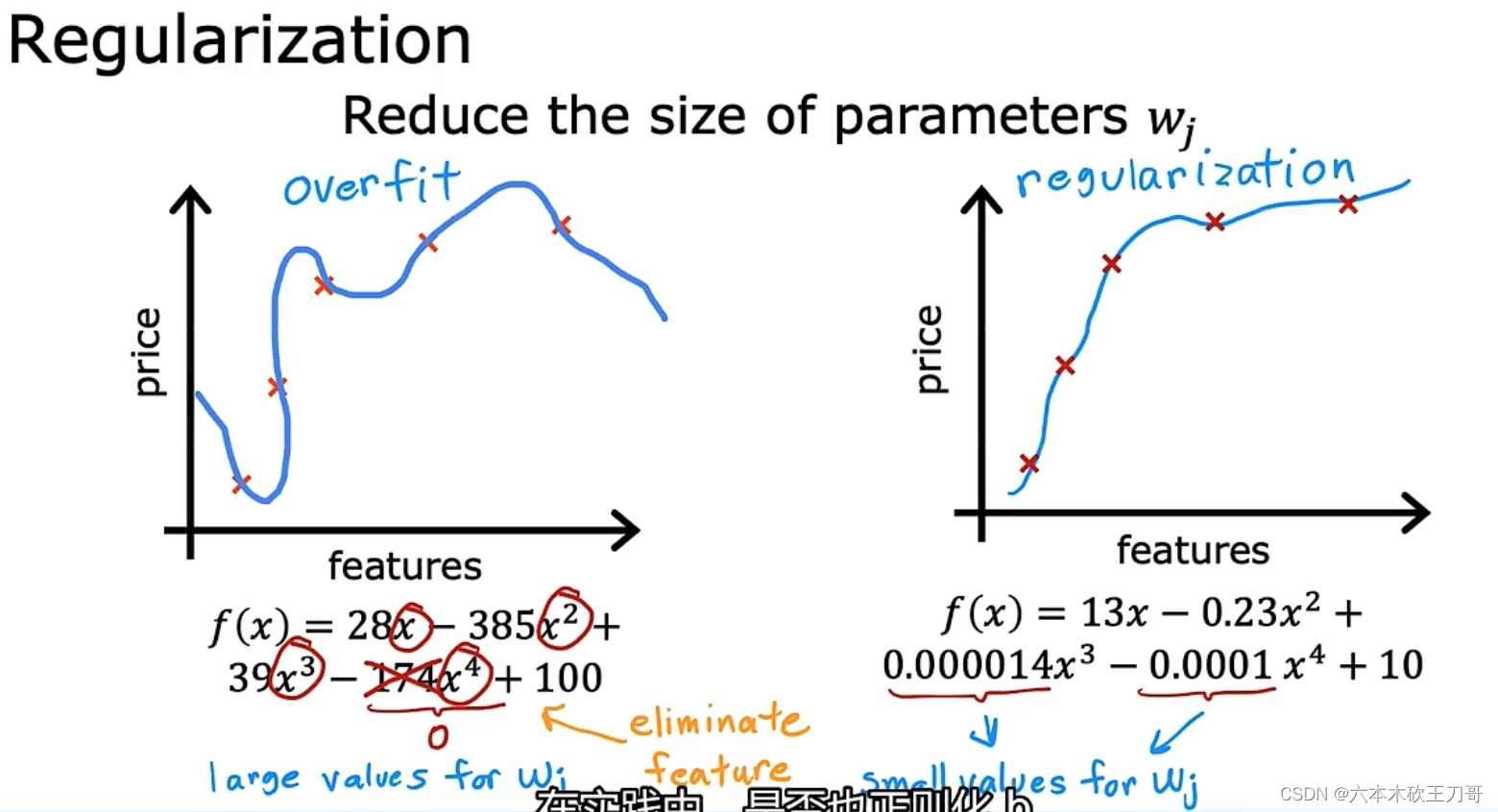
我们可以从之前的事例中看出,正是那些高次项导致了过拟合的产生,所以如果我们能让这些高次项的系数接近于 0 的话,我们就能很好的拟合了。
所以我们要做的就是在一定程度上减小这些参数w的值,这就是正则化的基本方法。我们决定要减少w3和w4的大小,我们要做的便是修改代价函数,在其中w3和w4 设置一点惩罚。 这样做的话,我们在尝试最小化代价时也需要将这个惩罚纳入考虑中,并最终导致选择较小一些的w3和w4。
下图的直觉告诉我们,在图一的代价函数基础上,如果增加两个系数较大的高次项,为了最小化代价函数,自然而然地w3,w4要接近于0,从而去除了这两项,相当于惩罚这两项使得原来的式子变为二次函数。在一般的回归函数中,使参数的值更小一般会使得曲线更为平滑而减少过拟合情况的发生。
通过这样的代价函数选择出的w3和w4 对预测结果的影响就比之前要小许多。
如果有很多参数,我们不清楚哪个参数是高阶项,即不知道惩罚哪个能获得更好拟合的结果,因此引入正则化项,统一惩罚参数以得到较为简单的函数。
统一惩罚能得到简单结果是因为,高阶项受到惩罚的效果会更强,反映在图像上就是使其影响变弱,λ 为正则化参数,有时候也会把b的惩罚加进来,但是大部分情况下只有w。
在下图中,第一项是平方误差项,+后的第二项为正则化项,λ 为正则化参数,作用是控制两个不同目标之间的取舍
(1)第一个目标与第一项 Usual Squared Error Function有关,即我们想要更加拟合数据集 fit data
(2)第二个目标与第二项 Regularization term 有关,即我们想要参数wj尽量小keep wj small,
惩罚从w1到wn,不包括b(之所以不惩罚b是为了让拟合的函数尽量简单,极端情况就是J = b,代表的一条水平线,不过实操中有无b影响不大)
上图中举了两个极端例子:
1. 若 λ 设置为0,等于没有进行正则化,出现过拟合情况;
2. 若 λ 设置的过大(上图中的10的10次方),即对w1 w2 w3 w4的惩罚程度过大,导致每一项都接近于0,最后假设模型只剩一个f(x) = b,出现欠拟合情况。所以对于正则化,我们要取一个合理的 𝜆 的值,这样才能更好的应用正则化。
所以对于正则化,我们要取一个合理的 𝜆 的值,这样才能更好的应用正则化。
回顾一下代价函数,为了使用正则化,让我们把这些概念应用到到线性回归和逻辑回归 中去,那么我们就可以让他们避免过度拟合了。
6.3 用于线性回归的正则方法 Regularized Linear Regression
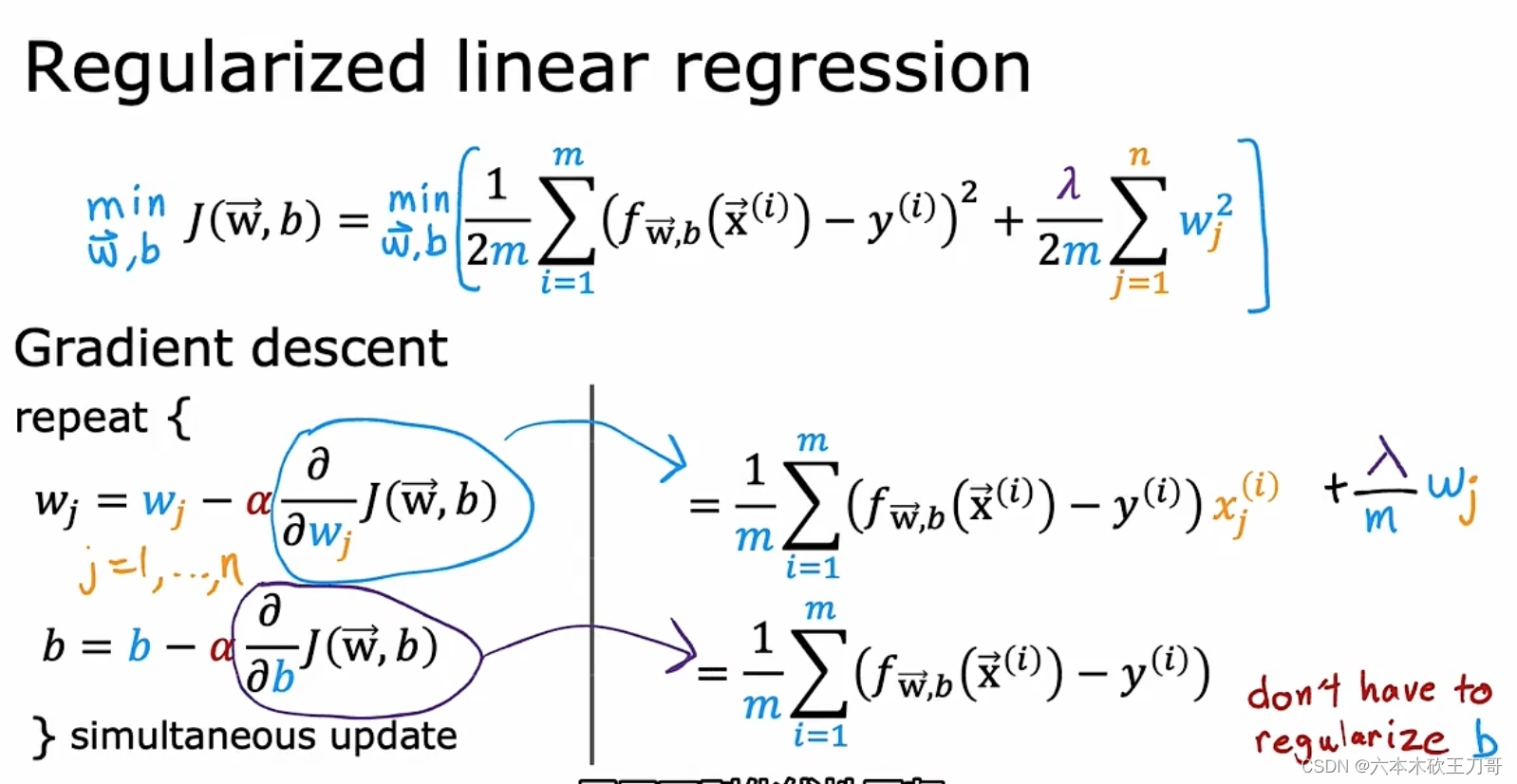
线性回归的正则化方法的推导过程如下,w比原来的更新多出了一项。
更新公式的数学推导,具体过程是展开并提项,从wj后面括号内的项可以看出,正则化就是在每一次执行gd迭代后,会用一个略微小于1的数乘以wj执行更新,让wj的值变小了一点,这就解释了为什么正则化可以在每次迭代中shrink缩小wj的值。
How we get the derivative term?
6.4 用于逻辑回归的正则方法 Regularized Linear Regression
针对逻辑回归问题,我们在之前的课程已经学习过两种优化算法:我们首先学习了使用梯度下降法来优化代价函数𝐽(w, b),接下来学习了更高级的优化算法,这些高级优化算法需要设计新的代价函数𝐽(w, b)。
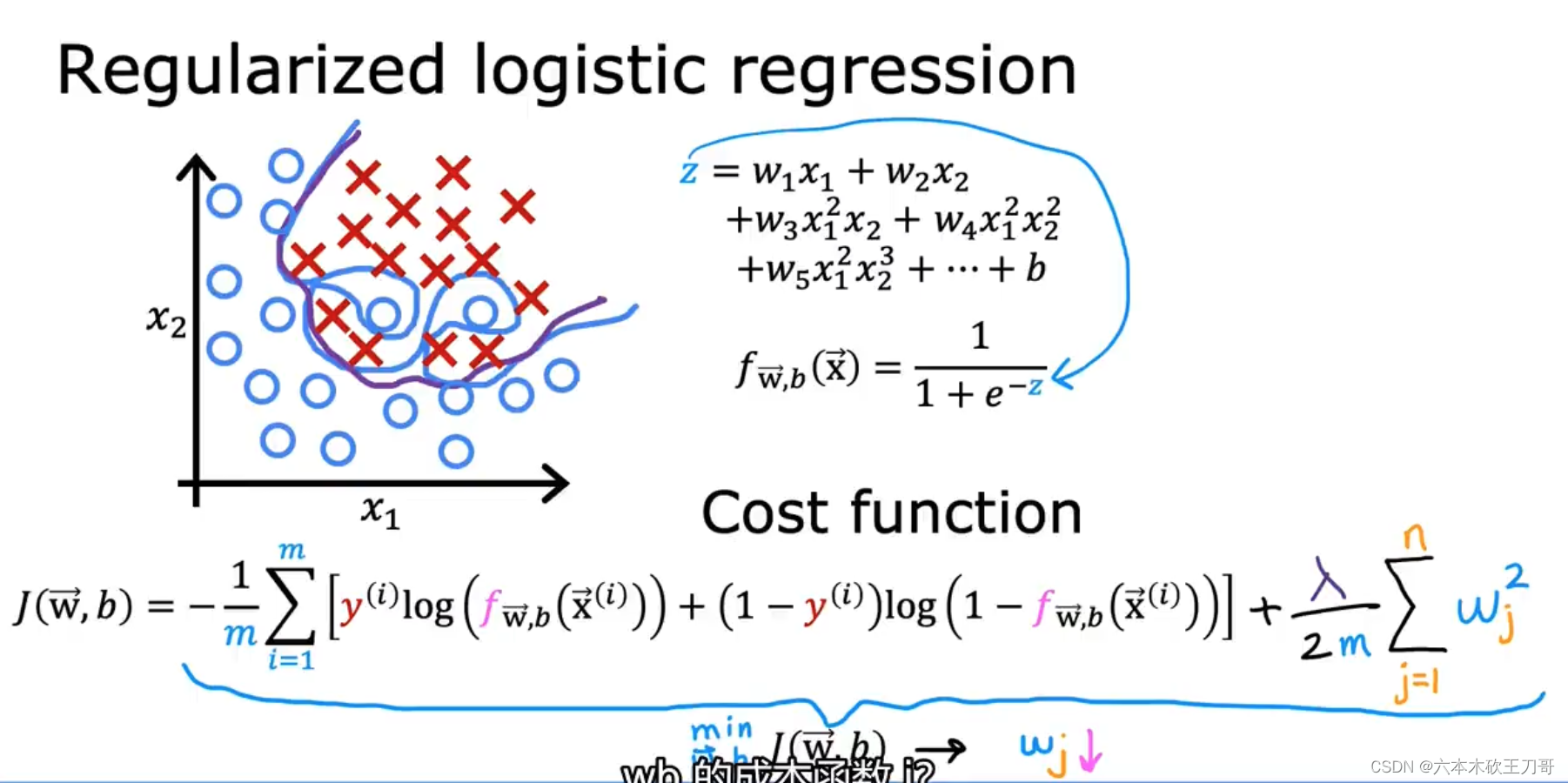
正则化同样对于逻辑回归,我们也给代价函数增加一个正则化的表达式,得到代价函数:
要最小化该代价函数,通过求导,得出梯度下降算法为:
看上去同线性回归一样,但是知道逻辑回归是用的Sigmoid函数,所以本质上不同。
目前大家对机器学习算法可能还只是略懂,但是一旦你精通了线性回归、高级优化算法和正则化技术,坦率地说,你对机器学习的理解可能已经比许多工程师深入了。现在,你已经有了丰富的机器学习知识,目测比那些硅谷工程师还厉害,或者用机器学习算法来做产品。
接下来的课程中,我们将学习一个非常强大的非线性分类器,无论是线性回归问题,还是逻辑回归问题,都可以构造多项式来解决,并且知道如何解决过拟合问题。你将逐渐发现还有更强大的非线性分类器,可以用来解决多项式回归问题。我们接下来将学会,比现在解决问题的方法强大 N 倍的学习算法。