一.实验内容

1. 编写程序实现n皇后算法，画出运行时间与皇后n的关系图，分析实验结果

二.实验过程及记录结果

主要算法

// 判断当前位置是否可以放置皇后
int is_valid(int* board, int row, int col) {
    for (int i = 0; i < row; i++) {
        if (board[i] == col || abs(board[i] - col) == abs(i - row)) {
            return 0;
        }
    }
    return 1;
}
void backtrack(int* board, int row, int n) {
    if (row == n) {
        count++;
        return;
    }
    for (int col = 0; col < n; col++) {
        if (is_valid(board, row, col)) {
            board[row] = col;
            backtrack(board, row + 1, n);
            board[row] = -1;
        }
    }
}

完整代码

#include <stdio.h>
#include <stdlib.h>
#include <time.h>

int count = 0; // 用于计数摆放种数

// 判断当前位置是否可以放置皇后
int is_valid(int* board, int row, int col) {
    for (int i = 0; i < row; i++) {
        if (board[i] == col || abs(board[i] - col) == abs(i - row)) {
            return 0;
        }
    }
    return 1;
}

// 回溯算法求解n皇后问题
void backtrack(int* board, int row, int n) {
    if (row == n) {
        count++;
        return;
    }
    for (int col = 0; col < n; col++) {
        if (is_valid(board, row, col)) {
            board[row] = col;
            backtrack(board, row + 1, n);
            board[row] = -1;
        }
    }
}

int main() {
    int n;
    printf("请输入皇后的个数：");
    scanf("%d", &n);

    int* board = (int*)malloc(n * sizeof(int));
    for (int i = 0; i < n; i++) {
        board[i] = -1;
    }

    clock_t start_time = clock(); // 记录开始时间
    backtrack(board, 0, n);
    clock_t end_time = clock(); // 记录结束时间

    printf("皇后的摆放种数为：%d\n", count);
    printf("程序运行时间为：%f秒\n", (double)(end_time - start_time) / CLOCKS_PER_SEC);

    free(board);
    return 0;
}

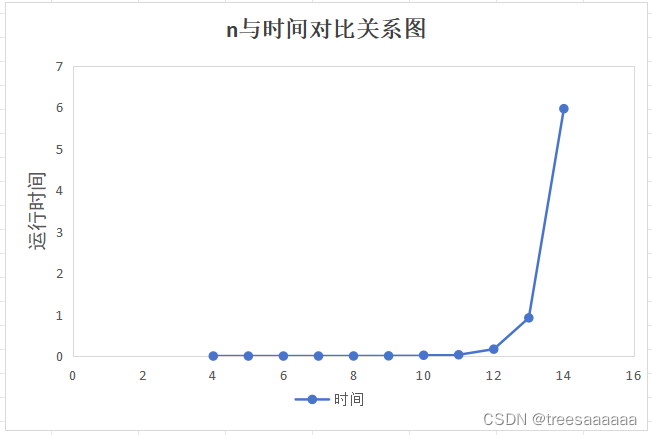
皇后数n（3<n<14）的时间效率对比

4.结果分析

实验结果：由运行结果可视化分析可以得出，当n逐渐增大后，运行时间呈指数型上涨趋势

5.原因分析：

 当n较小时（例如n=1, 2, 3），n皇后问题可以通过简单的算法快速解决。然而，随着n的增加，问题的复杂性也会急剧增加。当n较大时（例如n>10），即使使用优化的回溯算法，解决n皇后问题也可能需要相当长的时间。

1. 搜索空间大小：随着皇后数量的增加，可能的解的数量呈指数级增长。对于n皇后问题，有大约4^(n-1)种可能的解。因此，当n较大时，需要搜索的解空间变得非常大。

2. 回溯深度：在回溯算法中，每次决策都会导致一个解空间分支的产生。对于n皇后问题，每一步都有2种选择（将皇后放在当前列的某一行或某一行都不放）。因此，在每一步上都有2^n个可能的决策。由于有n个皇后需要放置，所以总共有2^(n-1)个决策步骤。这导致了一个非常深的搜索树，使得算法的运行时间急剧增加。由于n皇后问题具有指数级的状态空间（即可能的皇后位置的数量），因此它的时间复杂度是O(N!)，其中N是棋盘的大小，即n。这是因为在最坏的情况下，我们需要尝试所有可能的皇后位置组合。

3. 剪枝策略：为了提高效率，可以使用一些剪枝策略来减少搜索空间的大小。例如，如果当前列的某一行已经放置了皇后，那么可以提前终止该分支的搜索。然而，这些策略只能在一定程度上减少搜索空间的大小，并不能从根本上解决n皇后问题的复杂性。

6.总结

综上所述，随着皇后数量的增加，解决n皇后问题的运行时间会急剧增加。这是因为问题的解空间呈指数级增长，导致搜索树的深度非常深。因此，当需要解决的n皇后问题规模较大时，需要使用更高效的算法或近似算法来解决问题。