背包九讲——分组背包问题

背包问题第六讲——分组背包问题

背包问题是一类经典的组合优化问题，通常涉及在限定容量的背包中选择物品，以最大化某种价值或利益。问题的一般描述是：有一个背包，其容量为C；有一组物品，每个物品有重量w和价值v。目标是选择一些物品放入背包，使得它们的总重量不超过背包容量，同时总价值最大。
分组背包问题是背包问题的变体，它的一般描述为对物品进行分组，对每一组内的物品规定只能选择k个。

分组背包问题

分组背包问题（Grouped Knapsack Problem）是组合优化中的一个问题，它是经典的背包问题的变种。在分组背包问题中，有多个物品组，每组中的物品不可分割，并且每组中的物品数量至少有一个。目标是在不超过背包容量的前提下，选择物品的组合，使得总价值最大。

它在一组物品中进行选择，每个物品属于某个特定的组。问题的描述通常是这样的：给定若干组物品，每组物品都有自己的重量、价值以及数量限制。目标是选择若干组物品放入背包中，使得背包中物品的总价值最大。

问题定义

物品：有 n 组物品，每组有若干个不可分割的物品。
背包容量：背包可以承载的最大重量为 W。
价值：每组物品有一个价值。
重量：每组物品有一个重量。
目标：选择一些组的物品，使得总重量不超过 W，且总价值最大。

解题算法

动态规划：这是解决分组背包问题最常用的方法。
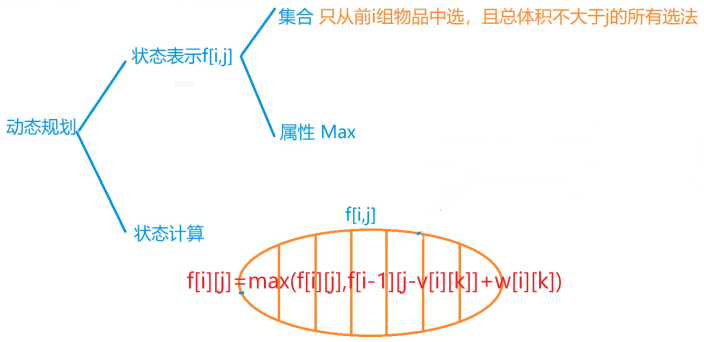
状态定义：定义f[i[j]表示考虑前 i 组物品，当前背包容量为 j 时的最大价值。
- 状态转移方程：
  - 如果不选第 i 组物品:f[i][j]=f[i-1][j]
  - 如果选第 i 组物品（前提是 j 至少可以装下第 i 组物品）：f[i][j] = max(f[i][j], dp[i-1][j-w[i]] + v[i])
- 初始化:f[0][j]=0，因为没有物品时价值为0。
- 遍历顺序：先遍历物品组，再遍历背包容量。
贪心算法：在某些情况下，如果物品的价值和重量满足某种比例关系，可以使用贪心算法。
回溯法：尽管效率较低，但可以用来验证问题的解。

问题解法

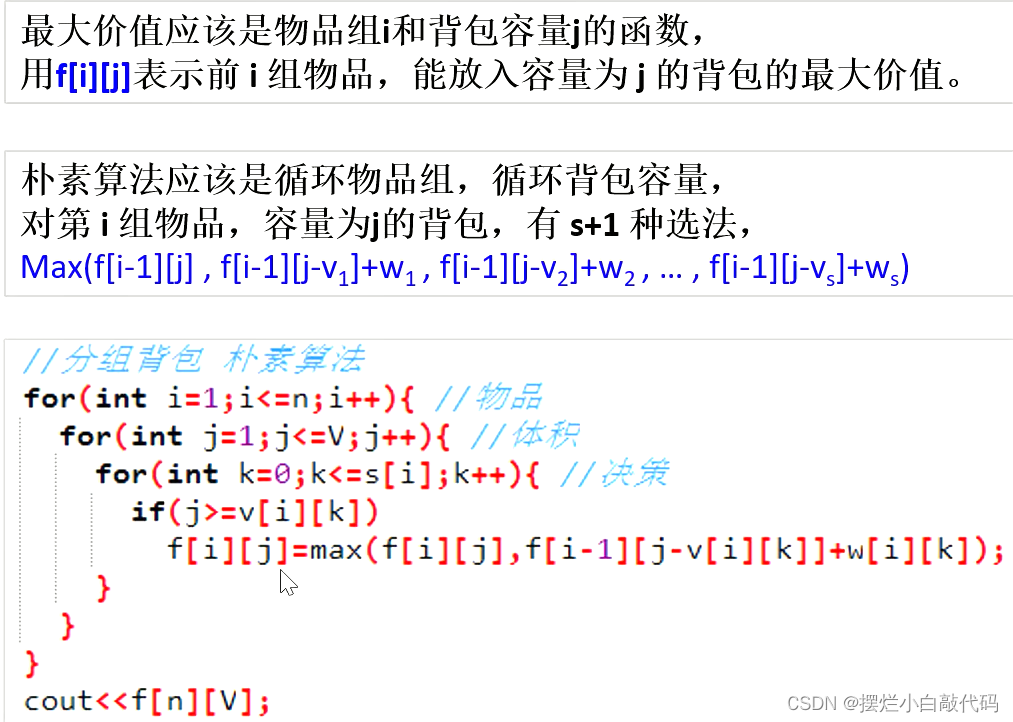
朴素解法：

这里朴素解法利用的二维数组f[i][j]来进行状态转移，枚举物品组数，枚举体积，枚举对于每组物品的决策，选还是不选，以得到最优解。这里朴素解法不再详细介绍，只放一个代码段，因为后面还可以优化一下。

其实看起来跟多重背包的朴素解法差不多，有什么不同的，下面放上了两段代码，比较看一下。不同在了就是在状态转移上了，多重背包呢可以选多个所以用k来控制，分组背包呢，例题中一组背包中最多只允许选一个，就是对于一组背包可以不选可以选一个。每一个物品都是不同的、有个性的，没有完全相同的，第三个for循环就是在枚举每一组具体的物品。

//多重背包朴素解法
for(int i=1;i<=n;i++){//物品
	for(int j=1;j<=V;j++){//体积
		for(int k=0;k<=s[i];k++){//决策
			if(j>=k*v[i]){
				f[i][j]=max(f[i][j],f[i-1][j-k*v[i]])+k*w[i];
			}
		}
	}
}
cout<<f[n][V]<<endl;

//分组背包朴素解法
for(int i=1;i<=n;i++){//第几组物品
	for(int j=1;j<=V;j++){//体积
		for(int k=0;k<=s[i];k++){//决策
			if(j>=v[i][k]){
				f[i][j]=max(f[i][j],f[i-1][j-v[i][k]]+w[i][k]);
			}
		}
	}
}
cout<<f[n][V]<<endl;

一维优化解法

对照朴素解法，多重背包呢时间复杂度那个for循环k的可以优化掉，空间复杂度也可以优化成一维的，但是时间复杂度优化是有条件的，多重背包呢可以组合进行二进制优化，也可以分类进行单调队列优化。分组背包呢，第i组物品的体积价值都是各不相同的，毫无规律可言，何以优化，但是在空间复杂度上可以优化成一维，f[i][j]是在f[i-1][j]转移过来的，就是在前一组物品决策完转移过来的，只是用了上一行的数据，有点类似01背包的一维优化，我们把此叫做滚动数组，前面的数据我更新完就不需要了，我只需要保存此时状态的数据即可，便于再下一次利用时可以拿来直接用。用完就可以释放掉，后面都不需要了，因此我们可以优化成一维解法。

#include<iostream>
using namespace std;
int dp[1005],v[1005],w[1005];//dp[i]表示背包容量为i时所获得最大价值
int N,V;
int main(){
	cin>>N>>V;
	int p;//p表示第p组物品
	for(int i=1;i<=N;i++){
		cin>>p;
		for(int j=1;j<=p;j++){
			cin>>v[j]>>w[j];
		}
        //因为dp[j]会先于dp[j-v[k]]更新，所以dp[j-v[k]]的值等价于dp[i-1][j-v[k]]
		for(int j=V;j>=1;j--){//逆序枚举背包容量
			for(int k=1;k<=p;k++){
				if(j>=v[k]){
					dp[j]=max(dp[j],dp[j-v[k]]+w[k]);
				}
			}
		}
	}
	cout<<dp[V]<<endl;
	return 0;
}

注：这里注意枚举背包容量和枚举k顺序不可颠倒，不然dp[j-v[k]]的值就不等价于dp[i-1][j-v[k]]了。

变式题型

博主做过其他类型的题，但都是分组背包的变式。有的题呢，一组物品给你限定了选多少个，比如选2个3个，例题中最多选一个，这样的话就比较麻烦了，既要确定选了哪一组物品又要达到选几个的要求，还是再次基础上，利用贪心，在每一组背包选几个的要求基础上，使得每一组背包都是最优的就可以（01背包）。用背包容量去枚举每一组背包，再去加一个if判断是否达到选几个的要求。有的呢还会把物品乱序输入，让你自己根据输入的编号去分组好，再去进行选择。下面放一个我写过的题的代码，背包的组数打乱，需要自己组合背包这一类的问题（当然题中样例打乱）。

#include<iostream>
#include<vector>
using namespace std;
int w[31],c[31];
int dp[201];
int v,n,p,t;
int main(){
	cin>>v>>n>>t;//v容量n物品t组数
	vector<vector<int>> group(t+1);
	for(int i=1;i<=n;i++){
		cin>>w[i]>>c[i]>>p;//p属于第几组
		group[p].push_back(i);//把下标往里抛就行
	}
	for(int i=1;i<=t;i++){//与一维优化类似
		for(int j=v;j>=0;j--){
			for(int k=0;k<group[i].size();k++){
				int index=group[i][k];
				if(j>=w[index]){
					dp[j]=max(dp[j],dp[j-w[index]]+c[index]);
				}
			}
		}
	}
	cout<<dp[v]<<endl;
	return 0;
}
/*
10 6 3
2 1 1
3 3 1
4 8 2
6 9 2
2 8 3
3 9 3
*/
//20

上篇文章：背包九讲——二维费用背包问题-CSDN博客

分组背包呢，听起来就是分组分组……，无非还是01背包的变形，变形非常多，但是万变不离其宗，方法会了，其他变式也都迎刃而解。博主水平有限，能说的都在文章展现了，有错误的地方请大家指出，大家有疑问的地方随时可以私信我，看到必答。下一篇更新树形背包（有依赖的背包）。