💥💥💞💞欢迎来到本博客❤️❤️💥💥
🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者
⛳️座右铭:行百里者,半于九十。
📋📋📋本文目录如下:🎁🎁🎁
目录
💥1 概述
文献来源:
摘要:充分发挥流域梯级水电的调节作用,实现梯级水光系统的互补联合发电是促进清洁能源消纳的重要途径。文中考虑光伏出力不确定性,以整体可消纳电量期望最大为目标,提出了梯级水光互补系统的短期优化调度模型。该模型以机组为最小调度单位,精细化建模了电站约束、机组约束以及电网约束,通过梯级负荷在电站和时段间的合理调配,挖掘梯级水电的电网供电支撑和光伏互补协调双重作用,提升互补系统整体消纳水平。模型求解方面,采用分段线性逼近、引入0-1整数变量、发电水头离散等线性化方法和建模技巧处理模型中的非线性约束,将原模型转换为混合整数线性规划问题,并在Java环境中采用CPLEX工具实现求解。最后,以参考中国西南地区某流域梯级的4个水电站15台机组以及2个光伏群构建的互补系统为例,验证了所提模型和求解方法的有效性。
关键词:
梯级水电站;优化调度;多能互补系统;最大化可消纳电量期望;混合整数线性规划;
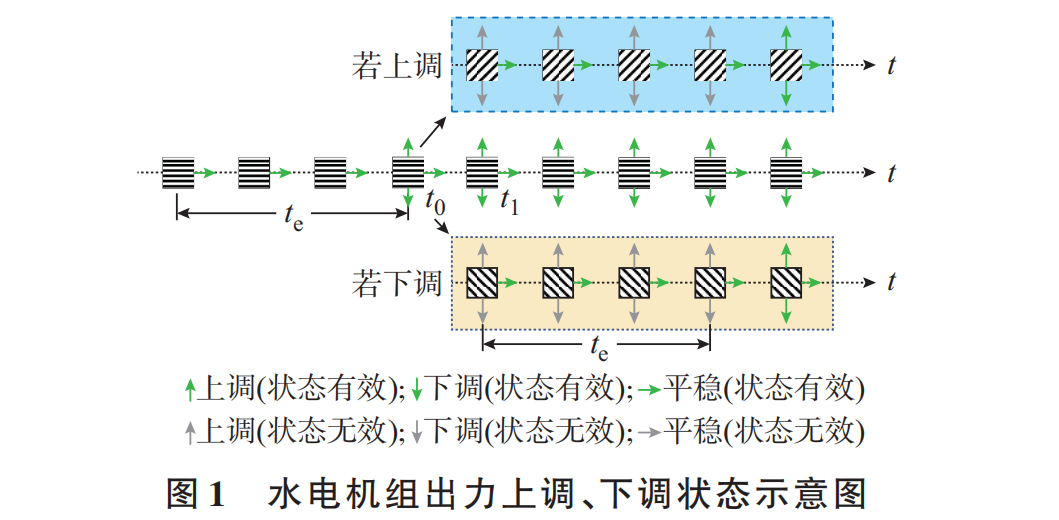
目前,关于水电与光伏等新能源的多能互补,除了互补系统的容量规划与设计[5-7] 之外,其运行调度也得到了广泛关注[8]。文献[9]分别以总出力波动性最小和整体平稳性最优为不同的控制策略,构建了水光互补系统调度模型;文献[10]考虑光伏出力随机性,提出了基于多项式混沌理论的概率配点算法的运行安全分析方法,为梯级水光互补系统安全稳定运行提供了理论支持;文献[11]考虑光伏的短期波动性,提出了嵌套短期弃电风险的水光互补中长期优化调度方法;文献[12]建立了龙羊峡水光互补短期优化调度模型,并分析了多种场景下的水光互补效果;文献[13]以光伏能量损失函数为基础建立短期与长期调度模型间的联系,提出了一种水光互补系统的自适应运行规则;文献[14]建立了兼顾发电量和出力波动的双目标调度模型,在保证发电量的前提下降低了光伏出力波动;文献[15]以梯级水电耗水量最小为目标,构建了梯级水光联合发电
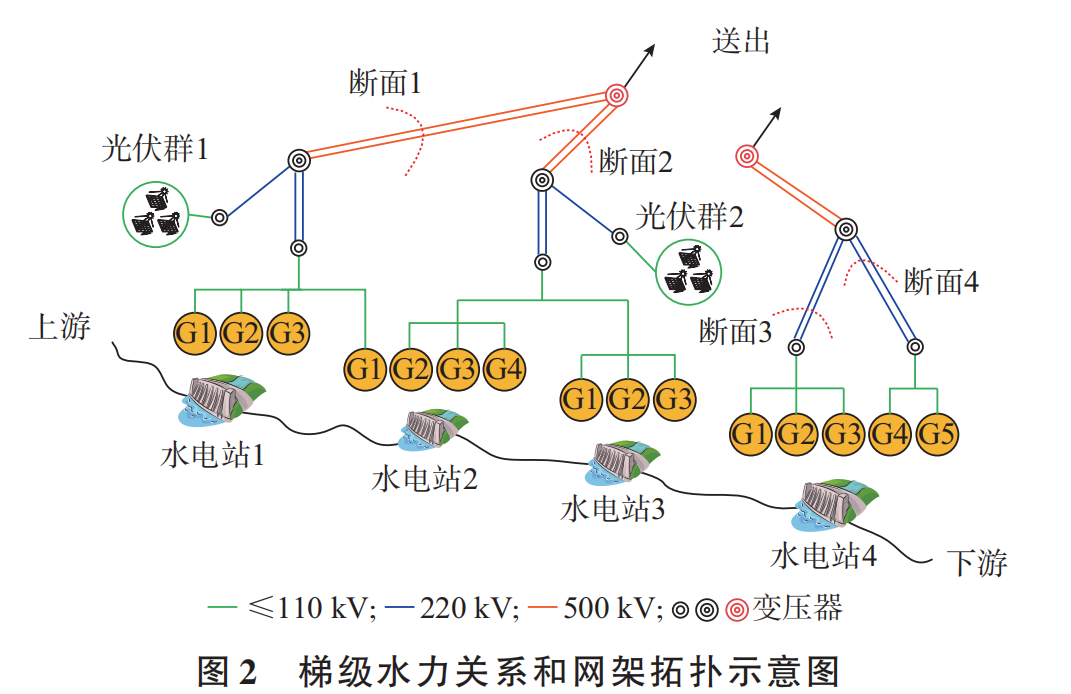
系统短期优化调度模型。综合调研分析,水光互补的本质是发挥水电的良好调节能力以促进随机性光伏的消纳,研究主要集中在互补特性分析、出力波动平抑、运行安全分析等方面。现有模型大多以电站为最小调度单元,没有精细化考虑机组和电网的复杂运行约束,使得各电站在执行计划时存在偏差,甚至难以执行。例如,同一电站可能包含多台不同类型的机组,不同类型的机组具有不同的爬坡能力、振动区、启停次数等约束限制,不能一概而论;同一电站的不同机组、梯级上下游之间的不同电站可能通过不同的分区断面逐级并网,受到多级分区断面输送容量约束限制[16-17]。此外,平抑光伏的波动性可能导致水电出力频繁波动,给水电机组造成损耗和运行风险[18-19],如何在互补调度中避免水电出力的频繁波动也是需要重点考虑的问题。
为此,本文在已有研究的基础上,以机组为最小调度单位,采用模糊聚类方法构建出力场景描述光
伏不确定性,精细化考虑互补系统面临的电站约束、机组约束和电网约束,构建了梯级水光互补系统最大化可消纳电量期望短期优化调度模型。通过梯级负荷在电站和时段间的合理调配,挖掘梯级水电在电网供电支撑和光伏互补调节中的双重作用[20] ,提升互补系统的整体电量消纳水平。所提模型是一个高 维 的 多 变 量 、多 约 束 的 混 合 整 数 非 线 性 规 划 (MINLP)问题,已有研究多采用智能算法求解,求解结果优劣受初始解影响大且容易陷入局部最优解,难以保证收敛到全局最优解。伴随近些年商业求解工具的发展,混合整数线性规划(MILP)凭借算法成熟、求解效率高、结果稳定等优势,已在水电领域得到了广泛应用[21-24]。为实现模型的高效求
解,对于模型中涉及的非线性约束,采用分段线性逼近、引入 0-1 整数变量、发电水头离散等线性化方法和建模技巧,将原 MINLP 问题转化为 MILP 问题,并 在Matlab环 境 中 采 用 CPLEX 工 具 实 现 求 解 。 最后,以中国西南地区某流域梯级的 4 座水电站 15 台机组以及 2 个光伏群为参考所构建的互补系统为研究对象,验证了本文所提模型和求解方法的有效性。
📚2 运行结果

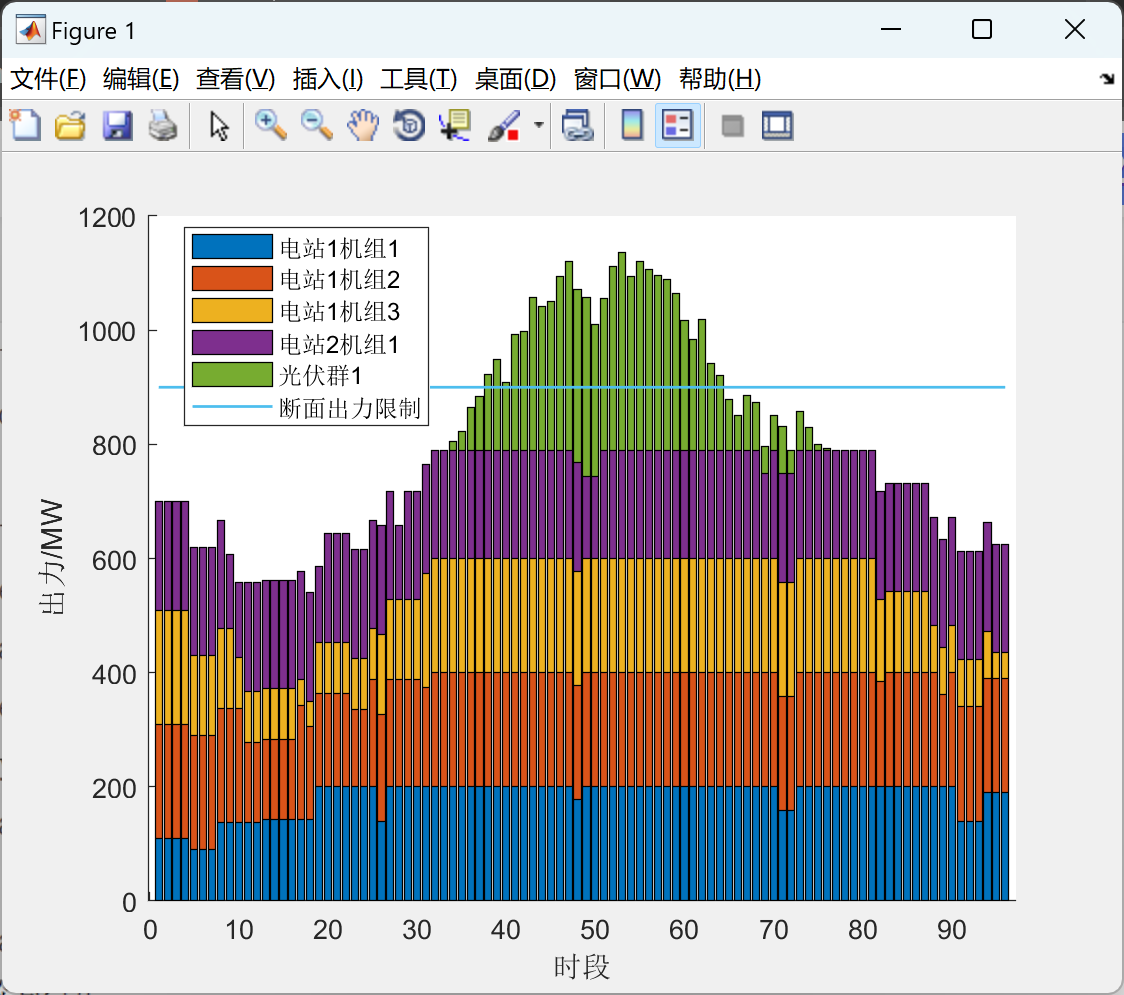
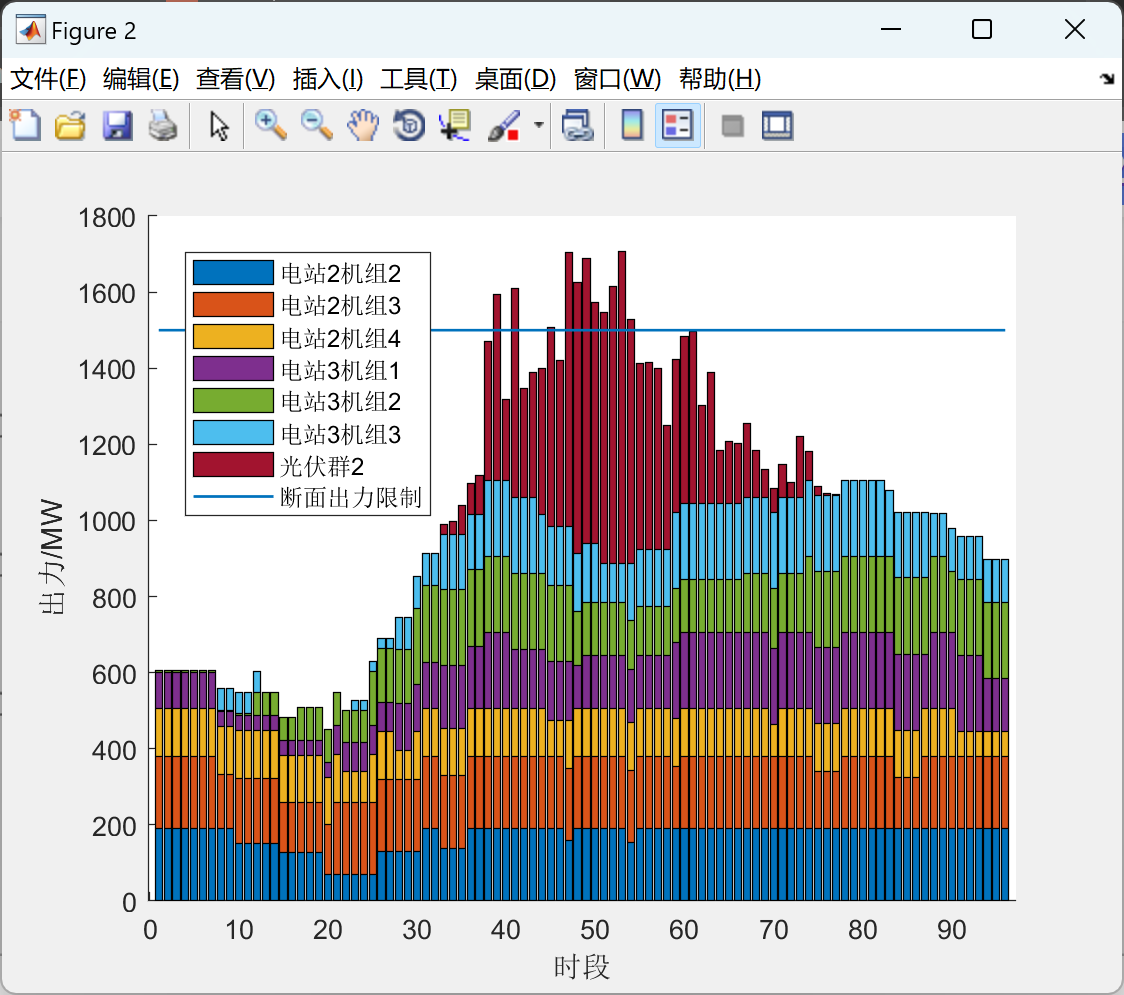
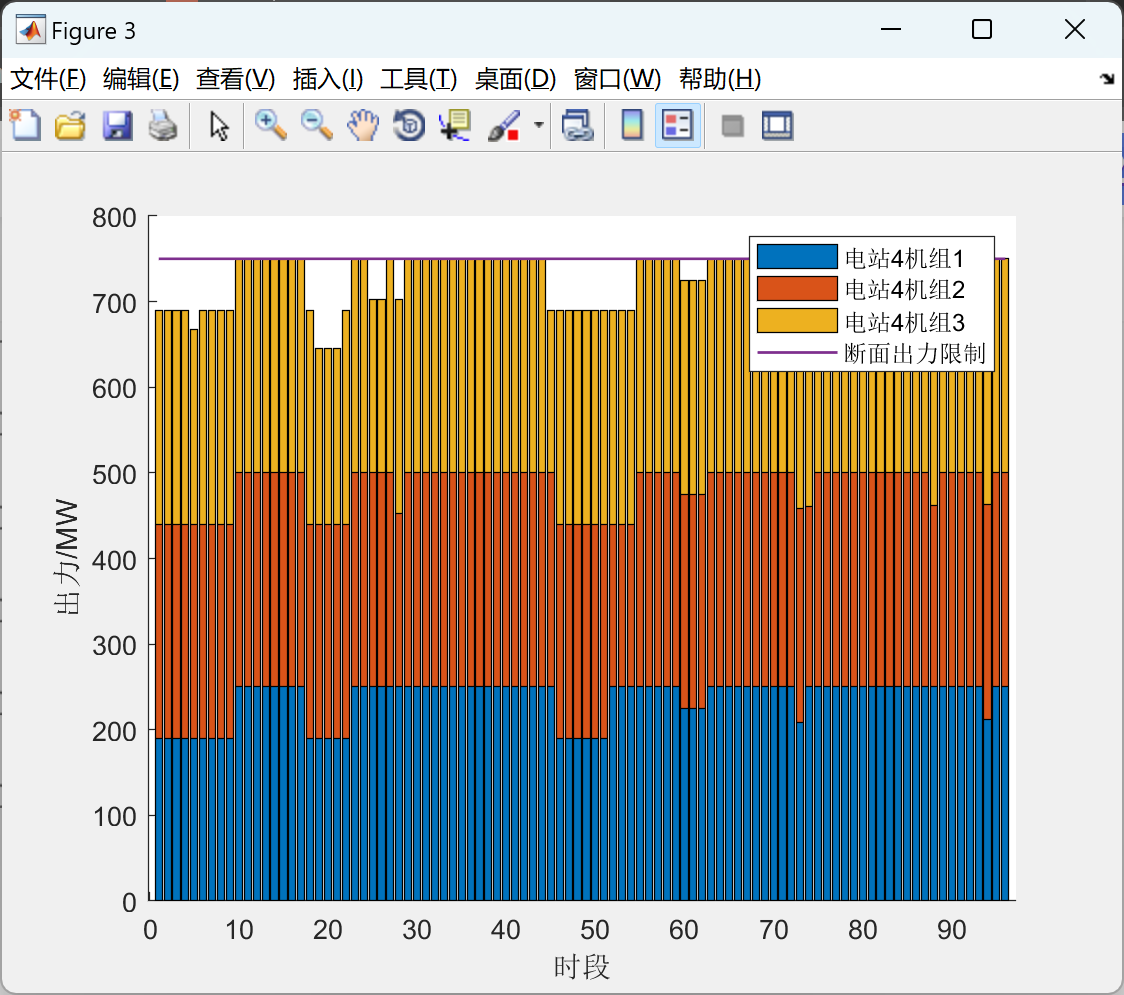
部分代码:
%% 决策变量
P_hydro = sdpvar(I,T); % 水电站i在时段t的出力
P_w = sdpvar(G,T); % 第g个约束断面在时段 t 的弃电量
V_it = sdpvar(I,T); % 水电站 i 在时段 t 末的库容
I_it = sdpvar(I,T); % 水电站i在时段t的入库流量
Q_it = sdpvar(I,T); % 电站 i 在时段 t的出库流量
R_it = sdpvar(I,T); % 电站i - 1和电站i之间在时段t的区间流量
Q_p_it = sdpvar(I,T); % 水电站i在时段t的发电流量
Q_d_it = sdpvar(I,T); % 电站 i 在时段 t 的弃水流量
Z_up_it = sdpvar(I,T); % 电站i所在水库在时段t的坝前水位
Z_down_it = sdpvar(I,T); % 水电站i在时段t的入库流量
P_int = sdpvar(N,T); % 第n台机组在时段t的出力
u_int = binvar(N,T); % 第n台机组在时段t的开停机状态
Q_p_int = sdpvar(N,T); % 第n台机组时段 t 的发电流量
y_on_int = binvar(N,T); % 第n台机组在时段t的启动操作变量
y_off_int = binvar(N,T); % 第n台机组在时段t的停机操作变量
H_int = sdpvar(N,T); % 第 n 台机组在时段 t的发电水头
H_loss_int = sdpvar(N,T); % 第 n 台机组在时段 t的水头损失
P_sgt = sdpvar(G,T); % 约束断面g在t时段所有机组总出力
theta_1_3ntk = binvar(10,T,2); % 水电站1-3的机组振动区指示变量
theta_4ntk = binvar(5,T,3); % 水电站4的机组振动区指示变量
alpha_int = binvar(N,T); % 1表示时段 t + 1 功率向下调节
beta_int = binvar(N,T); % 1表示时段 t + 1 功率向上调节
🎉3 参考文献
部分理论来源于网络,如有侵权请联系删除。
[1]罗彬,陈永灿,刘昭伟等.梯级水光互补系统最大化可消纳电量期望短期优化调度模型[J].电力系统自动化,2023,47(10):66-75.