目录
一、实验目的
掌握贪心算法求解问题的思想;针对不同问题,会利用贪心算法进行问题建模、求解以及时间复杂度分析;并利用JAVA/C/C++等编程语言开展算法编码实践(语言自选)。
理解装载问题及背包问题的贪心求解策略;对比分析与动态规划求解问题的算法异同;能够利用贪心算法,开展装载问题及背包问题的算法设计及编码实现。
二、实验环境
1、机房电脑 Window11
2、Eclipse/Dev-C++等
三、实验内容
实验要求及原理:
①掌握贪心算法求解问题的策略及思路;
能够用贪心算法解决的问题一般都具有两个重要性质:贪心选择性质和最优子结构性质。
1.贪心选择性质
贪心算法求解的问题的整体最优解可以通过一系列局部最优选择来达到,贪心算法不依赖将来所做的选择,也不依赖子问题的解,所以贪心算法一般是自顶向下解决问题。
2.最优子结构性质
当一个问题的最优解包含其子问题的最优解时,则此问题具有最优子结构性质。动态规划算法和贪心算法求解的问题都具有最优子结构性质。
②基于贪心算法设计装载问题的求解;
针对指定容量C的船,给定n个集装箱,各集装箱重量为wi。如何将集装箱装到船上保证装的集装个数最多?针对装载问题,如何利用贪心算法进行算法设计及优化。
问题分析:
wi越小可装载的集装箱个数越多,所以采用优先选取重量轻的集装箱装船的贪心思路;将集装箱重量从小到大排列,重量最轻的先装,将尽可能多的集装箱装到船上,每一次选择重量最轻的,这样就保证了最终问题的解是最优解。
在装载算法中,由于排序步骤是主导因素,因此采用最优的排序算法时,时间复杂度为O(nlog n)。
③基于贪心算法设计背包问题的求解;
针对指定容量C的背包,给定n个物品,各物品具有重量wi、价值vi。如何选择物品装入背包,使得价值最大(未要求0/1性)?背包问题,贪心算法设计求解策略及优化。
问题分析:
首先计算每种物品的单位重量的价值:vi/wi,然后根据贪心选择策略将尽可能多的单位重量价值最高的物品放入背包。若将这种物品全部放入背包后,背包内总重量还未超过c,就选择单位重量价值次高的物品并尽可能多的装入背包,以此类推不断进行下去直到背包装满。
动态规划求解0/1背包问题的思路差异:
对于0/1背包问题,贪心算法得到的不是全局最优解,0/1背包只能用动态规划算法来解决,因为该问题具有约束条件和目标函数的特性,而动态规划可以通过记录子问题的解来避免重复计算,并逐步构建出全局最优解,系统地考虑所有可能的解和约束条件,能够找到全局最优解。
在设计背包问题中,我使用了快速排序算法进行排序,使用了最快速的排序算法,该算法的时间复杂度最优,也为O(nlogn)。
④对上述算法进行时间复杂性分析,并输出程序运行时间及运行结果。
算法的时间复杂度为O(nlog n)。
四、核心代码
void loading(float C, float w[], int x[], int n) {
// 创建一个数组来存储重量和原始索引的配对
// 将每个物品的重量和索引组成一个pair,存入items数组
pair<float, int> items[n];
for (int i = 0; i < n; i++) {
items[i] = make_pair(w[i], i);
}
// 按照重量进行排序
sort(items, items + n, compare);
// 初始化x数组为0
for (int i = 0; i < n; i++) {
x[i] = 0;
}
// 装载集装箱
for (int i = 0; i < n && items[i].first <= C; i++) {
x[items[i].second] = 1; // 标识为1,表示商品要取
C -= items[i].first; // 调整更新货船容量
}
}// 快速排序函数,递归地对数组进行排序
void quickSort(float arr[], float w[], float v[], int low, int high) {
if (low < high) {
// pi是分区索引,arr[pi]现在在正确的位置
int pi = partition(arr, w, v, low, high);
// 分别对分区前后的元素进行排序
quickSort(arr, w, v, low, pi - 1);
quickSort(arr, w, v, pi + 1, high);
}
}
// 根据单位重量价值对物品进行排序
void Sort(int n, float w[], float v[]) {
for (int i = 0; i < n; i++)
z[i] = v[i] / w[i]; // 用z[]存物品的单位重量价值
quickSort(z, w, v, 0, n - 1); // 调用快速排序函数进行排序
}五、记录与处理
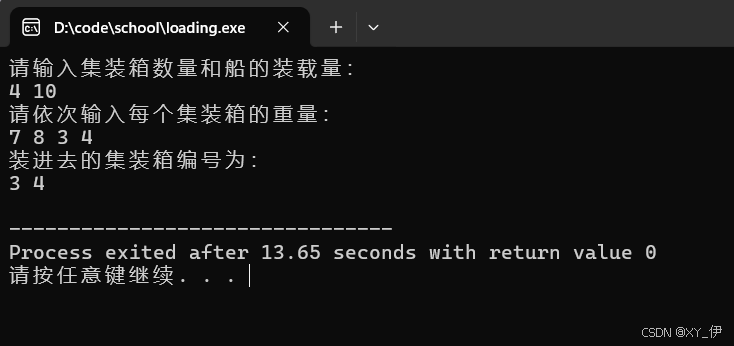
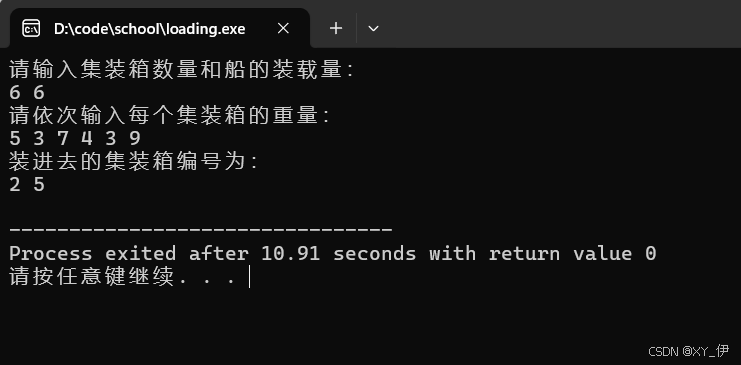
1.基于贪心算法设计装载问题的求解:
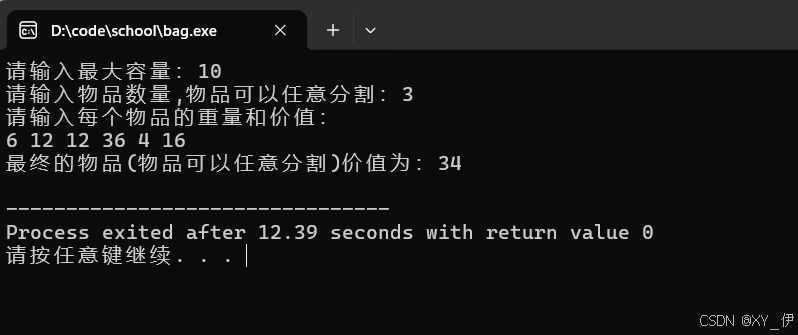
2.基于贪心算法设计背包问题的求解:
六、思考与总结
贪心算法是一种逐步构建解决方案的算法策略,贪心算法通过一系列局部最优选择来构建全局最优解,其关键在于每一步选择都是当前状态下的最佳决策,是自顶向下的策略,动态规划算法一般是自底向上解决问题。贪心具有两个性质:贪心选择性质和最优子结构性质。
七、完整报告和成果文件提取链接
完整可运行代码以及相关实验报告以下链接可获取:
链接: https://pan.baidu.com/s/1iss6-C2nxZQGkEpo-WDn0A?pwd=g5cg 提取码: g5cg