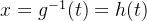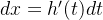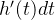一.定积分
定积分是微积分中的一个重要概念,用于求解函数在某个区间上的累积效应或面积。
1.定义
定积分
表示函数 f(x)在区间 [a,b]上的累积效应或面积。定积分的定义可以通过以下步骤来理解:
-
分割区间: 将区间 [a,b]分割成 n 个小区间,每个小区间的长度为 Δxi,其中
,且 x0=a,xn=b。
-
取样本点: 在每个小区间
内取一个样本点 ξi。
-
构造黎曼和: 构造黎曼和
,表示函数 f(x) 在区间 [a,b]上的近似累积效应或面积。
-
取极限: 当分割的区间数 n 趋向于无穷大,且每个小区间的长度 Δxi趋向于零时,黎曼和的极限即为定积分:
说明:
黎曼和是通过将区间 [a,b]分成 n 个等宽的子区间,每个子区间的宽度为
,然后选择每个子区间内的一点 xi,计算矩形的面积之和来近似积分的。
黎曼和可以表示为:
其中:
-
Sn是黎曼和的值。
-
n是子区间的数量。
-
xi是第 i个子区间 [xi−1,xi]内的一点。
-
Δx是每个子区间的宽度。
2.几何意义
定积分
的几何意义是函数 f(x) 在区间 [a,b]上的曲线下面积。具体来说:
-
如果 f(x)≥0,则定积分表示曲线下方的面积。
-
如果 f(x)≤0,则定积分表示曲线上方的面积的负值。
3.性质
定积分具有以下重要性质:
-
线性性质:
其中 c 和 d 是常数。
-
区间可加性:
其中 a≤c≤b。
-
积分上下限交换:
-
定积分中值定理
如果函数 f(x) 在闭区间 [a,b] 上连续,则存在 c∈[a,b],使得:
证明:
设f(x)在[a,b]上连续,因为闭区间上连续函数必有最大最小值,不妨设最大值为M,最小值为m,最大值和最小值可相等。
对
两边同时积分可得:
同除以b-a从而得到:
由连续函数的介值定理可知,必定
,使得
,即:
4.微积分基本公式
牛顿-莱布尼茨公式
其中,F(x)是 f(x)的一个原函数,即 F′(x)=f(x)。
微积分基本定理
微积分基本定理分为两部分,分别描述了积分上限函数的性质和定积分的基本公式。
第一部分(Part 1)
如果 f(t) 在区间 [a,b]上连续,则积分上限函数
在区间 [a,b] 上可导,并且其导数为:
第一基本定理表明不定积分是微分的逆运算,保证了某连续函数的原函数的存在性。
第二部分(Part 2)
如果 F(x)是 f(x)的一个原函数,即 F′(x)=f(x),则:
第二基本定理则提供了定积分和不定积分之间的联系,使得定积分的计算变得简便。
5.定积分换元法
步骤
-
选择合适的变量替换: 选择一个合适的变量替换 t=g(x),使得积分变得更简单,并求反函数:
-
求导数: 对 x 的导数
-
替换积分变量: 将原积分中的 x 替换为 t,并将 dx 替换为
-
确定新的积分上下限: 将原积分的上下限 a 和 b 替换为新的上下限 t 的值。即 t 的下限为 t1,上限为 t2。
-
求解新积分: 求解新的定积分
二.多元函数
1.二元极限
定义
设函数 f(x,y) 在点 (a,b) 的某个去心邻域内有定义。如果对于任意给定的正数 ϵ,总存在正数 δ,使得当
时,总有:
∣f(x,y)−L∣<ϵ
则称 L 为函数 f(x,y)在点 (a,b)处的极限,记作:
几何意义
当点 (x,y)从任意方式趋近于点 (a,b) 时,函数 f(x,y) 的值趋近于 L。换句话说,函数图像在二维平面的点 (a,b)附近趋近于一个三维立体平面上的点 (a,b,L)。可将(a,b)想象为(a,b,L)投影在二维平面的点。
如果 (x,y)从不同方式趋近于点 (a,b),函数 f(x,y) 的值不相等,则表示 f(x,y) 不存在。
2.偏导数
偏导数是多元函数求导的一种形式,表示在多个自变量中,当其中一个自变量改变而其他自变量保持不变时函数值的变化率。
这实质上是将其他自变量视为常数,然后按照单变量函数求导的方法进行运算。
定义
设函数 f(x,y) 在点 (x0,y0) 的某个邻域内有定义。如果极限:
存在,则称此极限为函数 f(x,y)在点 (x0,y0) 处对 x 的偏导数,记作:
类似地,如果极限:
存在,则称此极限为函数 f(x,y)在点 (x0,y0)处对 y的偏导数,记作:
偏导数的计算方法
对于二元函数z=f(x,y),求z对x的偏导数时,将y看作常量,对x求导;求z对y的偏导数时,将x看作常量,对y求导。
3.全微分
定义
如果函数z=f(x, y)在点(x, y)处的全增量
可以表示为
,其中A、B不依赖于Δx, Δy,仅与x, y有关,ρ趋近于0(ρ=√[(Δx)²+(Δy)²]),此时称函数z=f(x, y)在点(x, y)处可微分,AΔx+BΔy称为函数z=f(x, y)在点(x, y)处的全微分,记为dz即dz=AΔx +BΔy。
可微的必要条件条件
若z=f(x,y)在(x,y)点处可微,则偏导数
存在,并且
可微的充分条件
z=f(x,y)在(x,y)的某个邻域内有连续的偏导数
则在(x,y)处可微,
4.梯度
梯度是一个向量,表示多元函数在某一点处的最大变化率和变化方向。
定义
设 f(x1,x2,…,xn)是一个定义在 Rn(n维欧几里得空间) 上的多元函数,函数 f在n维向量点 a=(a1,a2,…,an)处的梯度定义为:
其中,
是函数 f 在点 a 处对第 i 个自变量的偏导数。
性质
-
最大变化率:梯度 ∇f(a) 的方向是函数 f在点 a 处变化率最大的方向。
-
变化率:梯度 ∇f(a) 的大小(模)是函数 f 在点 a 处沿梯度方向的变化率。
沿梯度方向是是函数 f在点 a 处变化率增加最大的方向;沿梯度反方向是是函数 f在点 a 处变化率减小最大的方向;沿梯度垂直方向函数 f在点 a 处变化率为0。
梯度下降
梯度下降是一种优化算法,用于寻找多元函数的最小值。其基本思想是沿着函数的负梯度方向逐步更新参数,以减少函数值。
算法步骤
-
初始化:选择一个初始点 x0。
-
迭代更新:对于每次迭代 k,计算当前点的梯度
,并更新参数:
其中,η 是学习率(步长),控制每次更新的步幅。
-
终止条件:当梯度的模足够小或达到预设的迭代次数时,停止迭代。通常,终止条件可以是以下几种:
-
梯度的模足够小:当梯度的模(或范数)
小于某个阈值时,停止迭代。
说明:
梯度的范数表示梯度向量的大小,即梯度向量的长度。
梯度的范数(模) ∥∇f(xk)∥是这个向量的欧几里得长度,定义为:
-
达到预设的迭代次数:当迭代次数达到预设的最大迭代次数时,停止迭代。
-
函数值变化足够小:当函数值的变化
小于某个阈值时,停止迭代。
-
学习率
学习率 η是一个重要的超参数,控制着每次更新的步幅。选择合适的学习率对于梯度下降算法的性能至关重要:
-
学习率过大:如果步幅过大,算法可能会“跳过”最优解,导致在最优解附近来回震荡。
-
学习率过小:可能导致算法收敛速度过慢。
5.二重积分
二重积分是多元微积分中的一个重要概念,用于计算二维区域上的函数积分。它通常用于计算平面区域上的面积、质量、重心等问题。二
重积分的基本思想是将一个二维区域分割成无数个小区域,然后在每个小区域上计算函数值的积分。
定义
设 f(x,y)f(x,y) 是定义在平面区域 D 上的函数,二重积分记作:
其中 dA表示面积元素。
几何意义
如果 f(x,y)是非负函数,二重积分
表示以 D 为底、以 f(x,y)为顶的曲顶柱体的体积。
二重积分的计算步骤-直角坐标系
在直角坐标系下,二重积分可以表示为两个定积分的乘积:
其中 D 是由 x=a 到 x=b 以及 y=g(x)到 y=h(x) 围成的区域。
-
确定积分区域 D:首先,你需要确定积分区域 D的边界。这个区域可以是矩形、圆形、多边形等。
-
设置积分限:根据积分区域 D,设置积分的限。例如,对于直角坐标系中的矩形区域,积分限通常是 a≤x≤b 和 c≤y≤d。
-
写出积分表达式:根据积分限写出二重积分的表达式:
-
计算内层积分:先对 y 进行积分,得到关于 x 的表达式。
-
计算外层积分:再对 x 进行积分,得到最终的积分值。
三.三角函数
1. 基本定义
-
正弦函数(sin):
-
余弦函数(cos):
-
正切函数(tan):
2. 基本关系
2.1 毕达哥拉斯恒等式
这个恒等式可以从直角三角形的勾股定理推导出来。
2.2 商数关系
2.3 倒数关系
3. 三角函数的周期性
-
正弦函数和余弦函数:
其中,k 是任意整数。
-
正切函数:
其中,k 是任意整数。
4. 三角函数的对称性
-
正弦函数:
-
余弦函数:
-
正切函数:
5. 三角函数的和差公式
-
正弦函数的和差公式:
-
余弦函数的和差公式:
-
正切函数的和差公式:
6. 三角函数的倍角公式
-
正弦函数的倍角公式:
-
余弦函数的倍角公式:
-
正切函数的倍角公式:
7. 三角函数的半角公式
-
正弦函数的半角公式:
-
余弦函数的半角公式:
-
正切函数的半角公式:


![[x_{i−1},x_{i}]](/image/aHR0cHM6Ly9sYXRleC5jc2RuLm5ldC9lcT8lNUJ4XyU3QmklMjV1MjIxMjElN0QlMkN4XyU3QmklN0QlNUQ%3D)







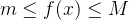
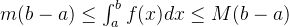
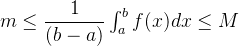
![\exists c\in [a,b]](/image/aHR0cHM6Ly9sYXRleC5jc2RuLm5ldC9lcT8lNUNleGlzdHMlMjBjJTVDaW4lMjAlNUJhJTJDYiU1RA%3D%3D)
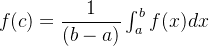
![\int _{a}^{b}f(x)dx=f(c)(b-a),\exists c\in [a,b]](/image/aHR0cHM6Ly9sYXRleC5jc2RuLm5ldC9lcT8lNUNpbnQlMjBfJTdCYSU3RCU1RSU3QmIlN0RmJTI4eCUyOWR4JTNEZiUyOGMlMjklMjhiLWElMjklMkMlNUNleGlzdHMlMjBjJTVDaW4lMjAlNUJhJTJDYiU1RA%3D%3D)