数据结构算法力扣总结1

文章目录

P3 认识复杂度和简单排序算法

1、时间复杂度

略

2、空间复杂度

创建有限的变量来运行代码，O(1)

如果需要创建一个数组，和之前数组同样规模，则应该是O(n)

3、冒泡排序算法

找出最大值

比如数组A[6] = {10,2,4,6,1,9}从小到大排序

从0开始，5和2判断谁大谁小，可以把数组变成：A[6] = {2,10,4,6,1,9}

之后的1，变成：A[6] = {2,4,10,6,1,9}，同理…，直到完成下标n-1的数的位置，{2,4,6,1,9,10}

一轮结束后，开始

{2,4,6,1,9}–》{2,4,1,6,9}

{2,4,1,6}–》{2,1,4,6}

{2,1,4}–》{1,2,4}

{1,2}–》{1,2}

{1}–》{1}

要从0就开始一次一次查看n-1个数，则为：n-1 + n-2 + n-3 +…，等差序列

时间复杂度：O(n^2)

代码

int[] nums = new int[]{9, 10, 4, 2, 5, 3, 1};
for (int i = nums.length - 1; i > 0; i--) {
    for (int j = 0; j < i; j++) {
        if (nums[j] > nums[j + 1]) {
            int temp = nums[j + 1];
            nums[j + 1] = nums[j];
            nums[j] = temp;
        }
    }
}

4、异或符号

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-HbeKGTki-1681106852036)(C:\Users\卯末\AppData\Roaming\Typora\typora-user-images\image-20230313183858028.png)]

注：3）的意思是：任何一团异或，最后结果都是一样的

应用

可以应用在数组中两个数交换顺序，也就是使用temp

前提是：两个数都在内存独立，两个指向的内存不一样

代码

// nums[j] = 1; nums[j+1] = 2
nums[j] = nums[j + 1] ^ nums[j];     // j+1=2   j=1     j=2^1
nums[j + 1] = nums[j + 1] ^ nums[j]; // j+1=2   j=2^1   j+1=2^2^1=0^1=1
nums[j] = nums[j + 1] ^ nums[j];     // j+1=1   j=2^1   j=1^2^1=0^2=2
// 结果:nums[j] = 2; nums[j+1] = 1

题目（常见面试题）

查找一个数组中出现奇数次的元素，nums = [1,1,2,3,3,5,5,5,5]

使用一个常数去异或所有元素，因为偶数次的元素自己异或2次变成0，而奇数次的则依然存在

1）当只有一种数出现奇数次，则直接用常数去异或整个数组，最后出来的就是出现奇数次的那个数

2）当有两种数出现奇数次，在使用1）的步骤之后，会求出a^b，而且因为出来的不是0，说明a和b是有某一位数是不一样的，分别是0和1，此时我们去除

// arr中，只有一种数，出现奇数次
public static void printOddTimesNum1(int[] arr) {
    int eor = 0;
    for (int i = 0; i < arr.length; i++) {
        eor ^= arr[i];
    }
    System.out.println(eor);
}

// arr中，有两种数，出现奇数次
public static void printOddTimesNum2(int[] arr) {
    int eor = 0;
    for (int i = 0; i < arr.length; i++) {
        eor ^= arr[i];
    }
    // a 和 b是两种数
    // eor != 0
    // eor最右侧的1，提取出来
    // eor :     00110010110111000
    // rightOne :00000000000001000
    // 问：这里~eor + 1能求出最右边的1，为什么呢？
    // 答：因为反转之前，最右边的1后边全是0，反转之后不就全变成1了，此时加上1，就会进行补点，1+1向上补点			  0，最后形成的就是只有最右边的1还依然是1，除了它之外全变成0了
    int rightOne = eor & (~eor + 1); // 提取出最右的1
	

    int onlyOne = 0; // eor'
    for (int i = 0 ; i < arr.length;i++) {
        //  arr[1] =  111100011110000
        // rightOne=  000000000010000
        // 这里这样做是为了筛选出a/b中这个位置有1的，因为偶数次的、这个位置有1的数，最后会因为有偶数次而		   成0，0^0^0^a/b = a/b，这样就筛选出来了
        if ((arr[i] & rightOne) != 0) {
            onlyOne ^= arr[i];
        }
    }
    System.out.println(onlyOne + " " + (eor ^ onlyOne));
}

5、选择排序算法

找出最小值

就是定义初始最小值，然后读取整个数组，发现比他小的就给minIndex赋值，执行完一个下标的最小之后，进行下一个下标的查找

代码

public static void selectionSort(int[] arr) {
   if (arr == null || arr.length < 2) {
      return;
   }
   // 0 ~ N-1  找到最小值，在哪，放到0位置上
   // 1 ~ n-1  找到最小值，在哪，放到1 位置上
   // 2 ~ n-1  找到最小值，在哪，放到2 位置上
   for (int i = 0; i < arr.length - 1; i++) {
      int minIndex = i;
      for (int j = i + 1; j < arr.length; j++) { // i ~ N-1 上找最小值的下标 
         minIndex = arr[j] < arr[minIndex] ? j : minIndex;
      }
      int tmp = arr[i];
      arr[i] = arr[minIndex];
      arr[minIndex] = tmp;
   }
}

6、插入排序算法

这个算法和之前的选择、冒泡不一样，会根据数组的排列而改变其时间复杂度

算法和冒泡排序差不多，但他是从开头开始算，而冒泡是结尾

是让0~i位置有序

冒泡是第一个for从后往前，第二个for从前往后，确定最后一个数的位置

插入两个for刚好相反，每次都做到0~j有序

时间复杂度分3个：O最差复杂度、Θ平均复杂度、Ω最好复杂度，问你复杂度就是问最差

该算法的时间复杂度为：O(n^2)

代码

// 从小到大排序
public static void insertionSort(int[] arr) {
   if (arr == null || arr.length < 2) {
      return;
   }
   // 不只1个数
   for (int i = 1; i < arr.length; i++) { // 0 ~ i 做到有序
      for (int j = i - 1; j >= 0 && arr[j] > arr[j + 1]; j--) {
         swap(arr, j, j + 1);
      }
   }
}

// i和j是一个位置的话，会出错
public static void swap(int[] arr, int i, int j) {
   arr[i] = arr[i] ^ arr[j];
   arr[j] = arr[i] ^ arr[j];
   arr[i] = arr[i] ^ arr[j];
}

P4 认识O(NlogN)的排序

1、二分查找算法

也就是min、max、mid

二分查找不一定是有序数组才能使用，也可以是无序的

代码

// 有序数组中是否有某一个数
public static boolean exist(int[] sortedArr, int num) {
   if (sortedArr == null || sortedArr.length == 0) {
      return false;
   }
   int L = 0;
   int R = sortedArr.length - 1;
   int mid = 0;
   // L..R
   while (L < R) { // L..R 至少两个数的时候
      mid = L + ((R - L) >> 1); // 这里不使用(L + R)>>1，是因为这样有溢出的危险
      if (sortedArr[mid] == num) {
         return true;
      } else if (sortedArr[mid] > num) {
         R = mid - 1;
      } else {
         L = mid + 1;
      }
   }
   return sortedArr[L] == num;
}

2、对数器

随机生成可控的数组，规定数组长度、元素范围、测试次数

代码

public static int[] generateRandomArray(int maxSize, int maxValue) {
   // Math.random()   [0,1)  
   // Math.random() * N  [0,N)
   // (int)(Math.random() * N)  [0, N-1]
   int[] arr = new int[(int) ((maxSize + 1) * Math.random())];
   for (int i = 0; i < arr.length; i++) {
      // [-? , +?]
      arr[i] = (int) ((maxValue + 1) * Math.random()) - (int) (maxValue * Math.random());
   }
   return arr;
}

public static void main(String[] args) {
   int testTime = 500000;// 测试次数
   int maxSize = 100;// 数组长度值
   int maxValue = 100;// 数组最大值
   boolean succeed = true;
   for (int i = 0; i < testTime; i++) {
       // 生成随机数组
      int[] arr1 = generateRandomArray(maxSize, maxValue);
       // 复制数组
      int[] arr2 = copyArray(arr1);
       // 执行数组
      selectionSort(arr1);
      comparator(arr2);
       // 对比正确答案和测试答案
      if (!isEqual(arr1, arr2)) {
         succeed = false;
         printArray(arr1);
         printArray(arr2);
         break;
      }
   }
   System.out.println(succeed ? "Nice!" : "Fucking fucked!");

   int[] arr = generateRandomArray(maxSize, maxValue);
   printArray(arr);
   selectionSort(arr);
   printArray(arr);
}

3、master公式

T(N) = a * T(N/b) + O(N^d)

当递归使用时，子规模相同，则符合master公式

a：子规模的数量

b：子规模的规模

d：除了子规模以外的时间复杂度

logb(a)和d的大小关系	时间复杂度
logb(a) < d	O(N^d)
logb(a) > d	O(N^logb(a))
logb(a) = d	O(N^d * logN)

4、归并排序算法

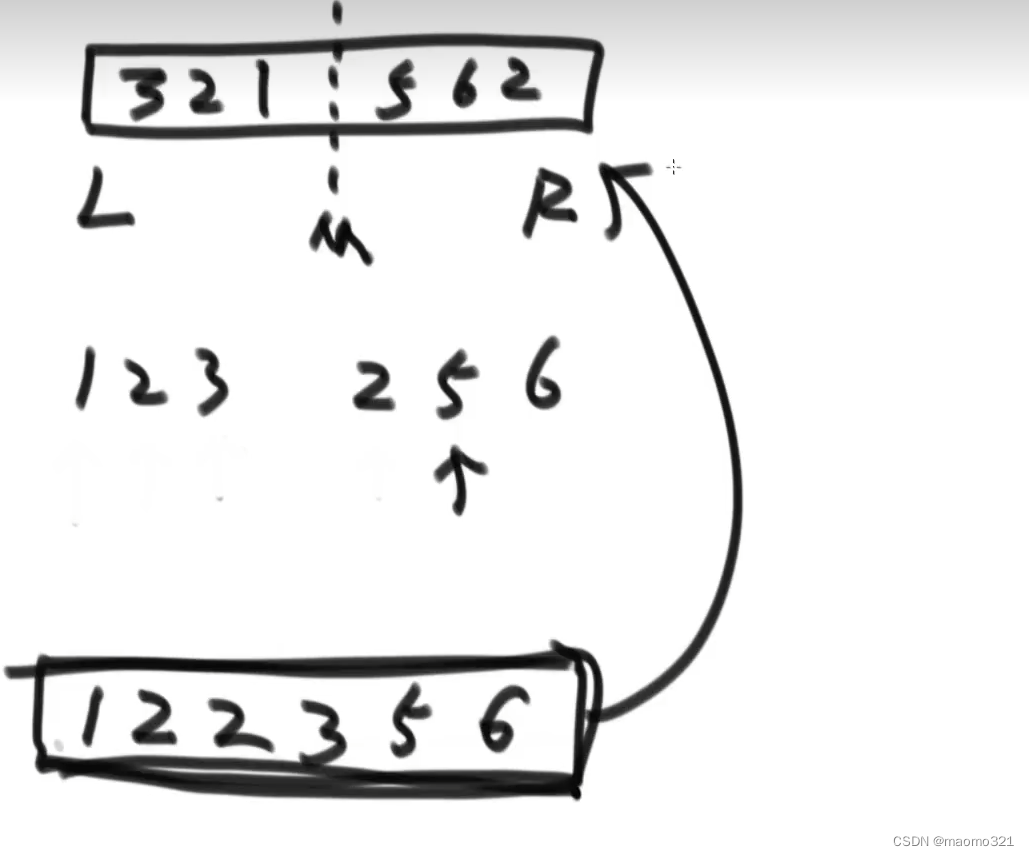
把数组分成两份，分别排好序，准备一个空数组，比较左边的第一个数和右边的第一个数，谁小就把这个数填到空

数组中，然后这个数组的指针向后移动一位，再次比较

问：为什么左右会有序

答：因为这个算法把数组分成很多份，之后每个都进行merge排序，每个都有自己的专属空数组

注：符合master公式，复杂度为O(N * logN)

图解

在这里插入图片描述

代码

// 请把arr[L..R]排有序
// l...r N
// T(N) = 2 * T(N / 2) + O(N)
// O(N * logN)
public static void process(int[] arr, int L, int R) {
   if (L == R) { // base case
      return;
   }
   int mid = L + ((R - L) >> 1);
    // 分成左右，左又分成它的左右，然后一直分
   process(arr, L, mid);
   process(arr, mid + 1, R);
   merge(arr, L, mid, R);
}

public static void merge(int[] arr, int L, int M, int R) {
   int[] help = new int[R - L + 1];
   int i = 0;
   int p1 = L;
   int p2 = M + 1;
   while (p1 <= M && p2 <= R) {
      help[i++] = arr[p1] <= arr[p2] ? arr[p1++] : arr[p2++];
   }
   // 要么p1越界了，要么p2越界了
   while (p1 <= M) {
      help[i++] = arr[p1++];
   }
   while (p2 <= R) {
      help[i++] = arr[p2++];
   }
   for (i = 0; i < help.length; i++) {
      arr[L + i] = help[i];
   }
}

和冒泡、选择的差别

没有把比较信息浪费掉，变成了整体有序的部分和更大的部分比较

数组小和问题

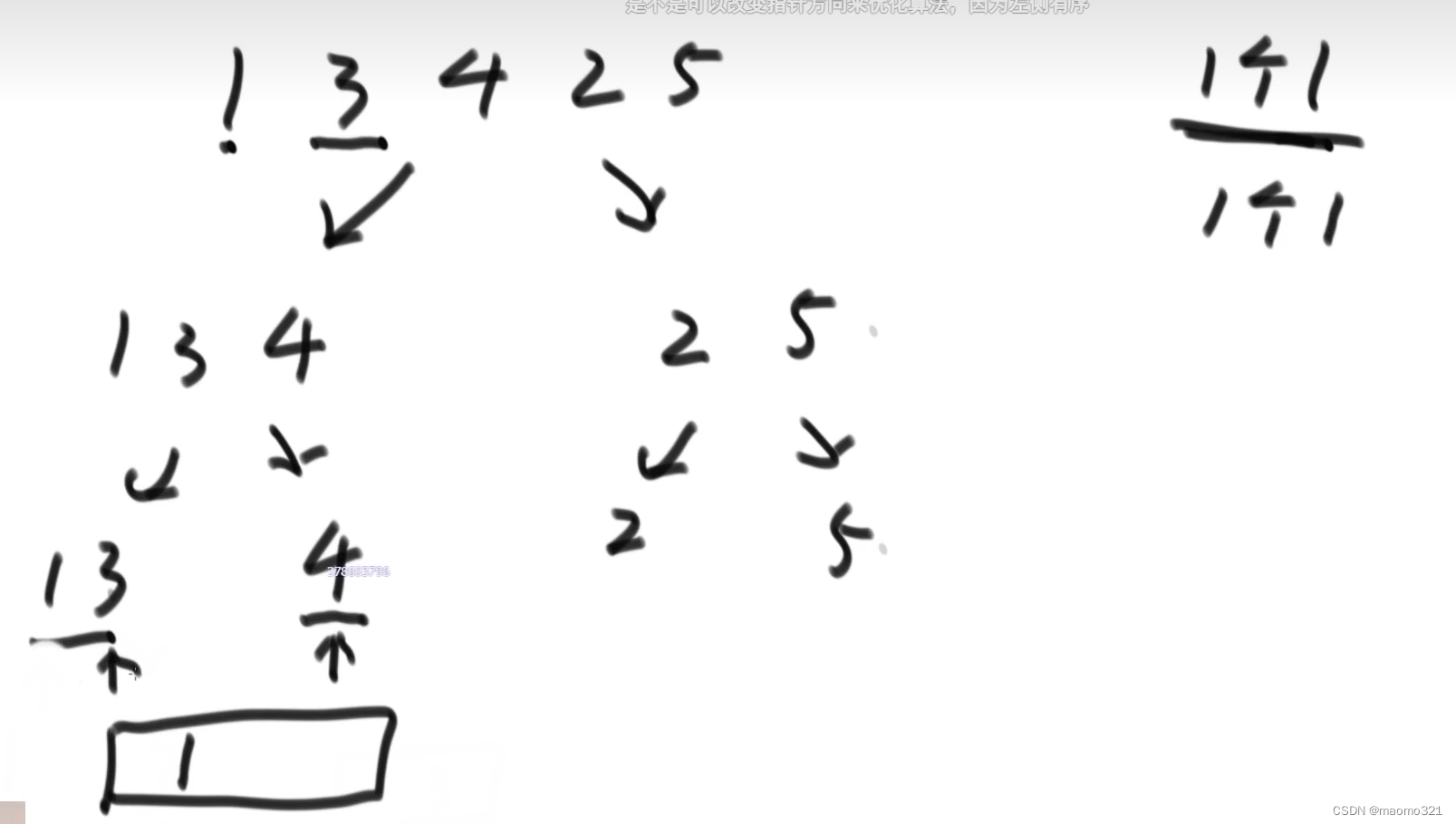
在这里插入图片描述

按照归并排序算法，把数组一个一个排号，对比左边和右边，如果左边小就在result加上该数

在这里插入图片描述

比如这里1 3，就两个数字都要和4对比，小了就写道新建的result数组里

算完1 3之后，算1 3 4，分为1和2 5，3 和2 5，4和2 5对比，同样是小了就加进去

注：当左边和右边相同时，右边需要先指针向下，而且不产生小和，这样才能直到当前这个数比右边多少个小

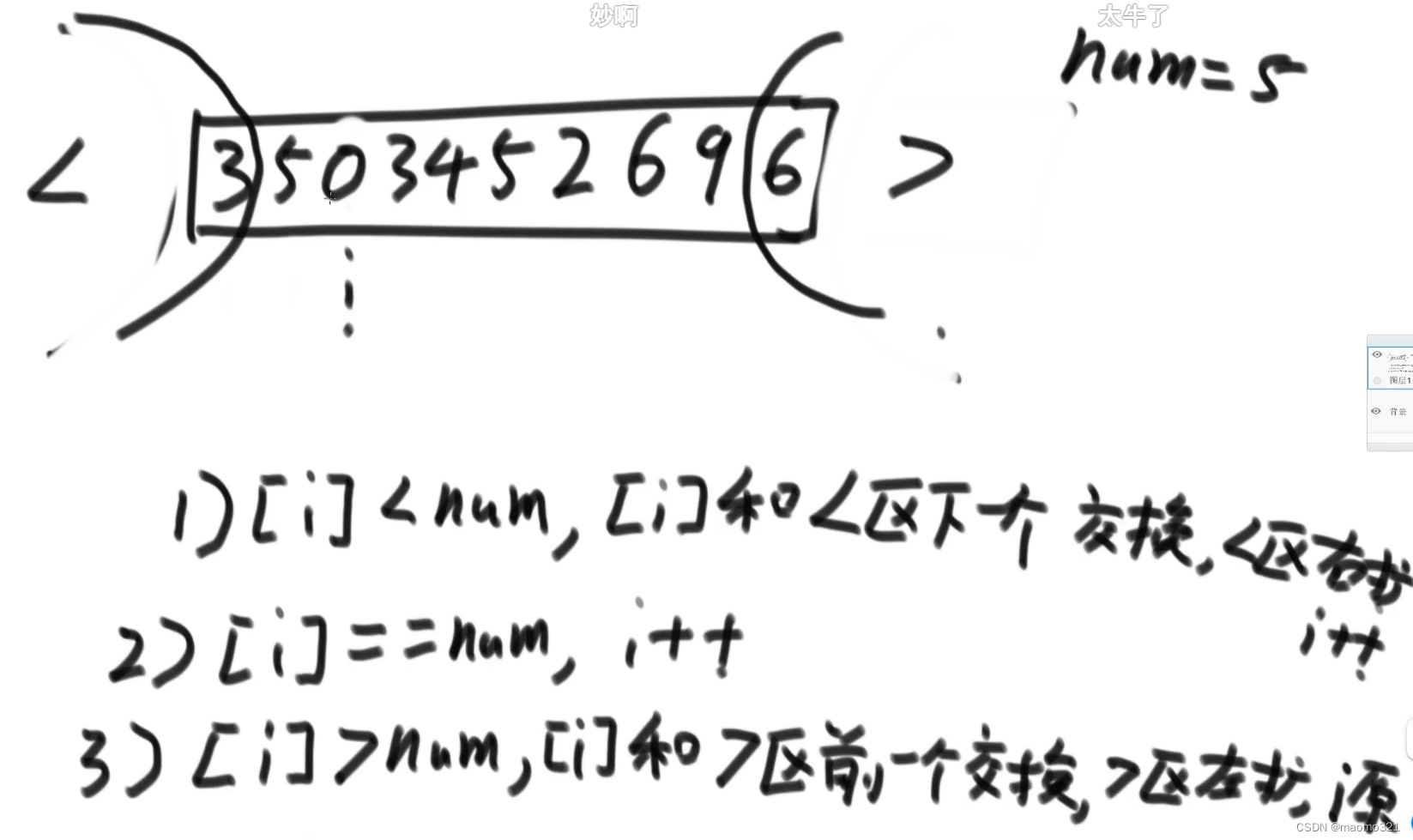
在这里插入图片描述

5、快速排序算法

荷兰国旗问题

问题：给出一个数组和num，比num小的放在左边，比num大的放在右边，和num相同的放在中间

在这里插入图片描述

也就是分出两个区域，一个大于一个小于，然后上面的规则

荷兰国旗进阶：快速排序

使用递归，在荷兰问题之后，根据小于部分右边界的数作为划分，再次进行荷兰国旗，大于部分也一样，以此类推

由于每次荷兰国旗问题都能出现一串或者一个准确的位置信息，所以终究是能排好的

改进之后可以使用random来提取随机数，根据这个数作为开始的划分数字，这样可以使时间复杂度随机

最优复杂度：O(N*logN)

最差复杂度：O(N^2)

空间复杂度：logN

代码

// 荷兰国旗问题
public static int[] netherlandsFlag(int[] arr, int L, int R) {
    if (L > R) {
        return new int[]{-1, -1};
    }
    if (L == R) {
        return new int[]{L, R};
    }
    int less = L - 1;
    int more = R;
    int index = L;
    while (index < more) {
        if (arr[index] == arr[R]) {
            index++;
        } else if (arr[index] < arr[R]) {
            swap(arr, index++, ++less);
        } else {
            // 这里不用index++，是因为把下标大的数换过来还需要验证他是否小于目标数
            swap(arr, index, --more); 
        }
        // System.out.println("less:" + less + ",more:" + more);
        // for (int j : arr) {
        //     System.out.print(j + ",");
        // }
        // System.out.println();
    }
    swap(arr, more, R); // 此时右边界已经不大于index，最后把目标数换到中间
    // for (int j : arr) {
    //     System.out.print(j+",");
    // }
    // System.out.println("");
    // 返回左边界和右边界，这里的“+1”是因为之前-1了
    return new int[]{less + 1, more};
}

public static void swap(int[] arr, int i, int j) {
   int tmp = arr[i];
   arr[i] = arr[j];
   arr[j] = tmp;
}


// 快排递归版本（结合上面的代码一起使用）
public static void quickSort1(int[] arr) {
    if (arr == null || arr.length < 2) {
        return;
    }
    process(arr, 0, arr.length - 1);
}

public static void process(int[] arr, int L, int R) {
    if (L >= R) {
        return;
    }
    // 生成随机的下标，将其所对应的数字和最后一个数交换
    // 左边界（会变）
    int ran = L + (int) (Math.random() * (R - L + 1));
    System.out.println("随机数：" + ran);
    swap(arr, ran, R);
    int[] res = netherlandsFlag(arr, L, R);
    process(arr, 0, res[0] - 1);
    process(arr, res[1] + 1, R);
}

P5 详解桶排序以及排序内容大总结

1、二叉树

完全二叉树和普通二叉树的区别

完全二叉树中每个节点要么是满的，要么有左节点，而且该左节点是最后一个节点

普通二叉树中就没有这么多要求

2、推结构（堆排序算法）

在这里插入图片描述

堆的高度也是logN级别的

题目

问1：如果给一串数字，要形成大根堆，那么应该怎么写？

答：二叉树中有个规律，左节点 = 父节点 * 2 + 1、右节点 = 父节点 * 2 + 2

比较左节点和右节点的大小，选出最大节点和父节点进行比较

如果父节点比较大，则不用操作，反之，需要让这个节点和父节点交换，之后再和下面的节点进行同样的操作

问2：如果给一个大根堆，去除其第一个节点，那么应该怎么做才能让这个堆依然是大根堆？

答：挑选最后一个节点，将其交换到已经去除的第一个节点上，然后堆总长度-1，之后就是和问1一样的操作了

问3：给一串数字，要求使用大根堆进行排序

答：先排序成为大根堆，之后大根堆的第一个节点和最后一个交换，交换之后，去除最后一个节点，再进行大根堆调整，把交换后的数字串变成大根堆，这样去除的节点就是最大值，以此类推，推出第二大，第三大。。。

代码

// 堆排序额外空间复杂度O(1)
public static void heapSort(int[] arr) {
    if (arr == null || arr.length < 2) {
        return; 
    }
    // O(N*logN)
    //		for (int i = 0; i < arr.length; i++) { // O(N)
    //			heapInsert(arr, i); // O(logN)
    //		}
    // O(N)
    // 排列成为大根堆，相比上面的，会快一点点，但时间复杂度是一样的
    for (int i = arr.length - 1; i >= 0; i--) {
        heapify(arr, i, arr.length);
    }
    int heapSize = arr.length;
    // 去除最大节点，之后交换最大节点和最小节点，这样最大值就排在了最后
    swap(arr, 0, --heapSize);
    // O(N*logN)
    while (heapSize > 0) { // O(N)
        heapify(arr, 0, heapSize); // O(logN)
        swap(arr, 0, --heapSize); // O(1)
    }
}

// arr[index]位置的数，能否往下移动
public static void heapify(int[] arr, int index, int heapSize) {
    int left = index * 2 + 1; // 左孩子的下标
    while (left < heapSize) { // 下方还有孩子的时候
        // 两个孩子中，谁的值大，把下标给largest
        // 1）只有左孩子，left -> largest
        // 2) 同时有左孩子和右孩子，右孩子的值<= 左孩子的值，left -> largest
        // 3) 同时有左孩子和右孩子并且右孩子的值> 左孩子的值， right -> largest
        int largest = left + 1 < heapSize && arr[left + 1] > arr[left] ? left + 1 : left;
        // 父和较大的孩子之间，谁的值大，把下标给largest
        largest = arr[largest] > arr[index] ? largest : index;
        if (largest == index) {
            break;
        }
        swap(arr, largest, index);
        index = largest;
        left = index * 2 + 1;
    }
}

public static void swap(int[] arr, int i, int j) {
    int tmp = arr[i];
    arr[i] = arr[j];
    arr[j] = tmp;
}

// arr[index]刚来的数，往上
public static void heapInsert(int[] arr, int index) {
    while (arr[index] > arr[(index - 1) / 2]) {
        swap(arr, index, (index - 1) / 2);
        index = (index - 1) / 2;
    }
}

问4：

在这里插入图片描述

答：使用小根堆进行操作，比如k = 4，数组为0123456789

此时先对0~3进行小根堆排序，得出的小根堆最小值放在0上

然后再对1~4进行小根堆排序，得出的小根堆最小值放在1上

以此类推，最后如果小根堆数目不够4个了，就直接把小根堆的值从上往下依次拿出即可

时间复杂度 = logk * N，因为N次实现小根堆，每次只有k个数字，固定有限个(k)步数

代码

public static void sortedArrDistanceLessK(int[] arr, int k) {
	if (k == 0) {
		return;
	}
	// 这里使用系统自带的小根堆（黑盒）
	// 底层是数组，当你一直添加东西时，数组会耗尽，这时候会成倍的扩容
	// 扩容时间复杂度：扩容次数 * 单个扩容时间复杂度
	//    N * logN     logN			N
	// 因为是成倍扩容：2 4 8 16，所以扩容次数为logN
	// 因为每次扩容都需要把原本数组的数拷贝一次，所以为N
    
    // 默认小根堆，如果想要使用大根堆，要改写比较规则，也就是比较器
    // PriorityQueue<Integer> heap = new PriorityQueue<>(new AComp());
	PriorityQueue<Integer> heap = new PriorityQueue<>();
	int index = 0;
	// 0...K-1
	for (; index <= Math.min(arr.length - 1, k - 1); index++) {
		heap.add(arr[index]);
	}
	int i = 0;
	for (; index < arr.length; i++, index++) {
		heap.add(arr[index]);
		arr[i] = heap.poll();
	}
	while (!heap.isEmpty()) {
		arr[i++] = heap.poll();
	}
}

黑盒

系统会提供一个推结构，可以理解为黑盒，你和黑盒沟通方式：你给他一个数（add），它返回一个数（poll）

它只能是提供一个数并且移除，例如max，但你不能要求改变黑盒数字的同时，还要黑盒给已经改变的堆结构

进行堆排序。

它也是能实现，但就是代价太高，不值得，宁愿自己写一个

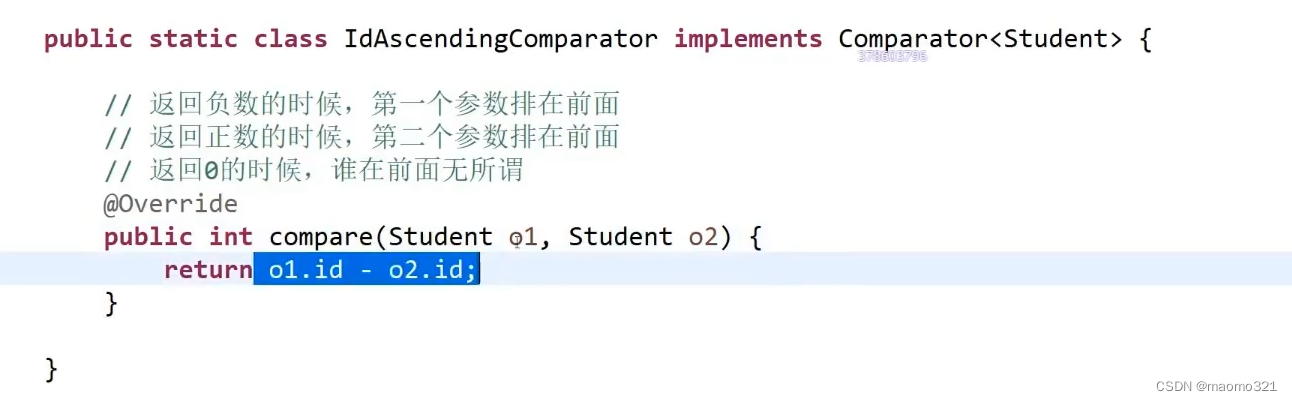
3、比较器

我们自己建造的常量，系统不能够帮我们比较，让他比较只会是比较两个的内存地址，没有意义

在这里插入图片描述

例如

在这里插入图片描述

这一串注释是所有比较器的潜规则

在这里插入图片描述

代码

// 比较器
public static class AComp implements Comparator<Integer> {
	// 如果返回负数，认为第一个参数应该拍在前面
	// 如果返回正数，认为第二个参数应该拍在前面
	// 如果返回0，认为谁放前面都行
	@Override
	public int compare(Integer arg0, Integer arg1) {
		return arg1 - arg0;
	}
}

// 比较器应用
public static void main(String[] args) {
	Integer[] arr = { 5, 4, 3, 2, 7, 9, 1, 0 };
	Arrays.sort(arr, new AComp());
    for (int i = 0; i < arr.length; i++) {
		System.out.println(arr[i]);
    }
}

// 输出
// 9 7 5 4 3 2 1 0

4、桶排序

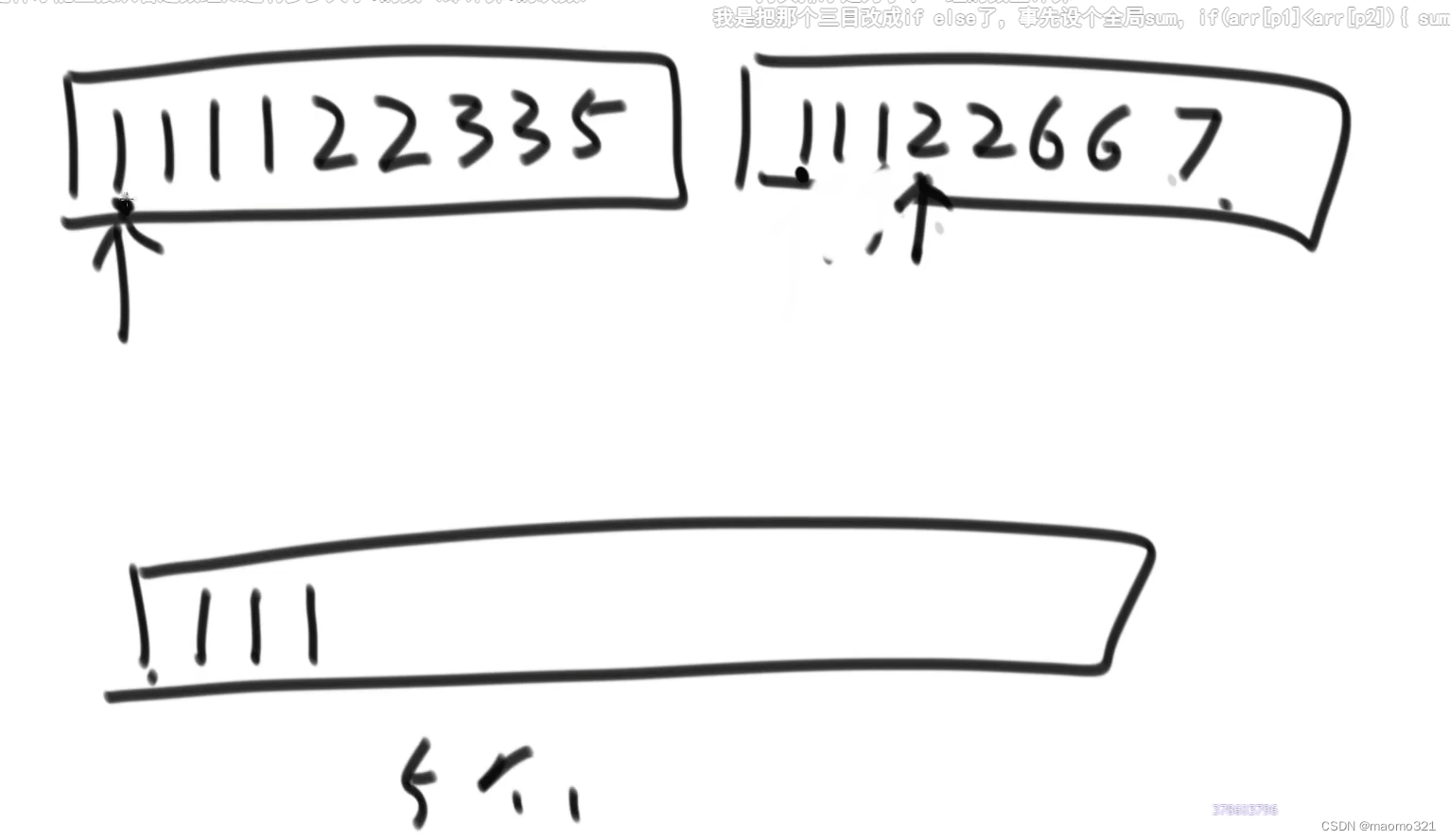
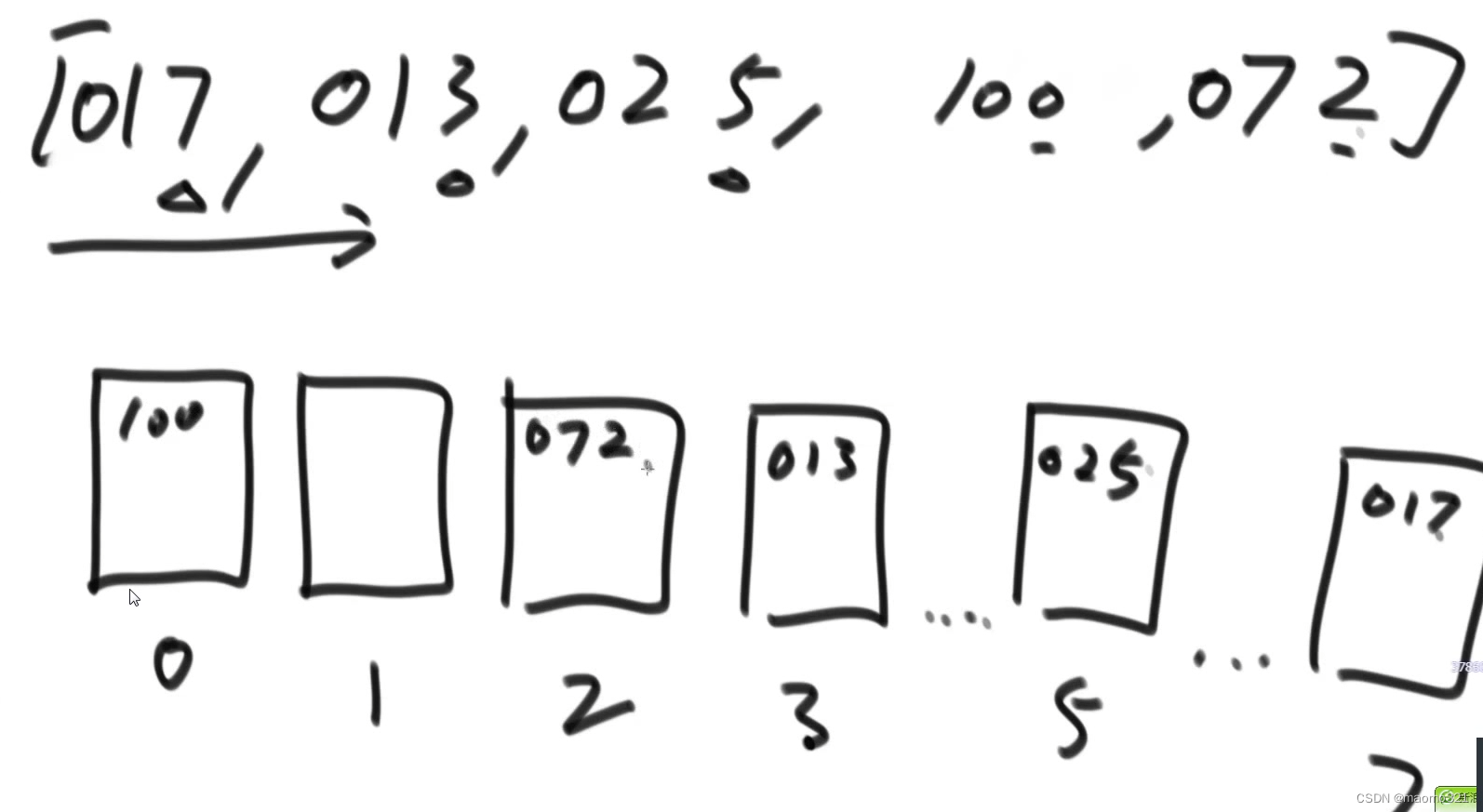
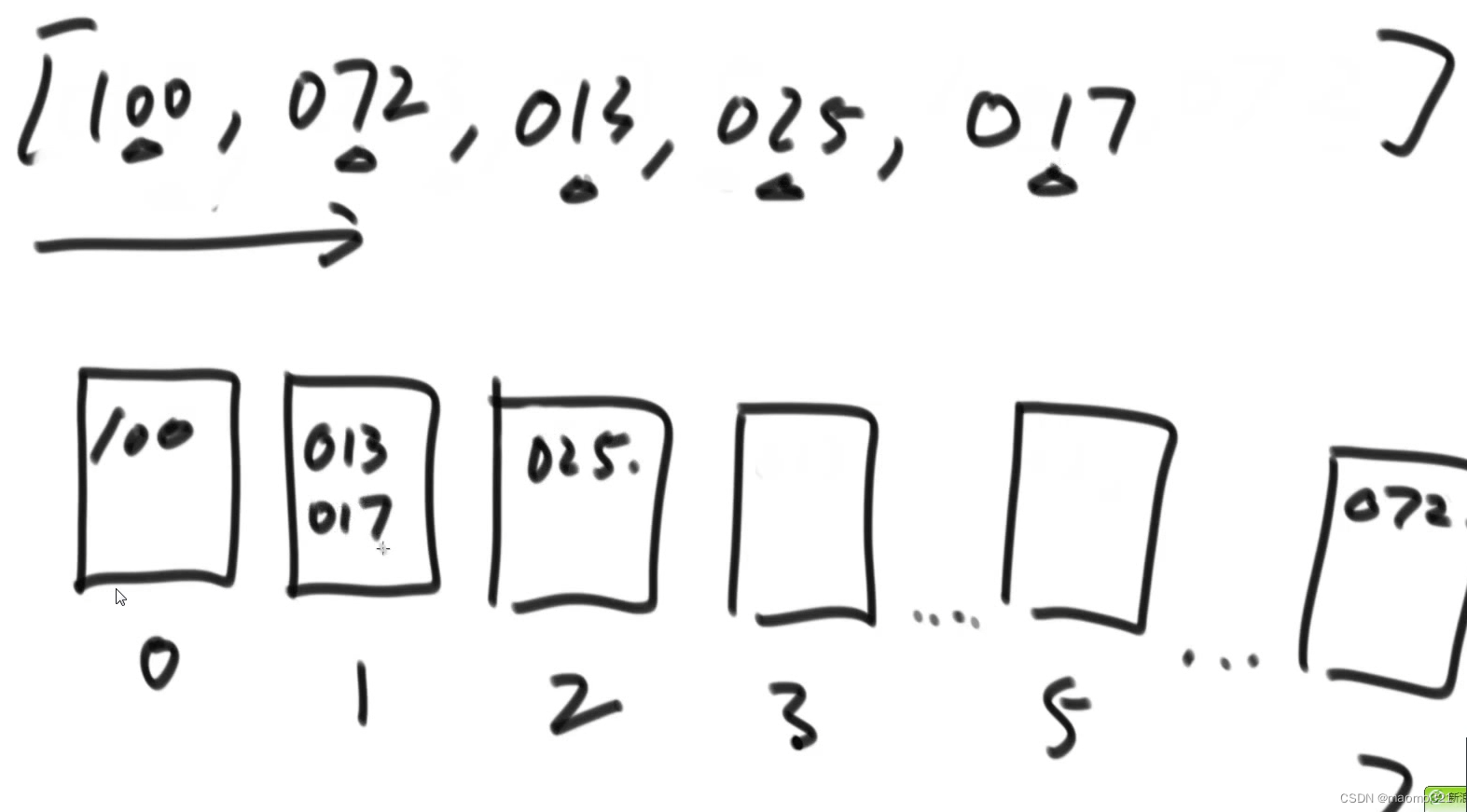
在这里插入图片描述

在应用之前，先把位数统一，如72->072

同一个桶里先放先出原则，不同桶当前比较的位数，谁较小谁先出

这里出来之后应该是[100、072、013、025、017]，再然后就是如下，直到位数达到最大

在这里插入图片描述

桶排序的代码实现原理：

先是按位填入桶中，从0开始看，发现个位是所对应数时，++，之后填下一位时，在上一位的基础上进行添加

在这里插入图片描述

之后按照后填入的先拿出的规则，从右往左，先拿出062，放在2所对应4 - 1 = 3上

代码

// only for no-negative value
public static void radixSort(int[] arr) {
	if (arr == null || arr.length < 2) {
		return;
	}
	radixSort(arr, 0, arr.length - 1, maxbits(arr));
}


// arr[L..R]排序  ,  最大值的十进制位数digit
public static void radixSort(int[] arr, int L, int R, int digit) {
   final int radix = 10;
   int i = 0, j = 0;
   // 有多少个数准备多少个辅助空间
   int[] help = new int[R - L + 1];
   for (int d = 1; d <= digit; d++) { // 有多少位就进出几次
      // 10个空间
      // count[0] 当前位(d位)是0的数字有多少个
      // count[1] 当前位(d位)是(0和1)的数字有多少个
      // count[2] 当前位(d位)是(0、1和2)的数字有多少个
      // count[i] 当前位(d位)是(0~i)的数字有多少个
      int[] count = new int[radix]; // count[0..9]
      for (i = L; i <= R; i++) {
         // 103  1   3
         // 209  1   9
         j = getDigit(arr[i], d);
         count[j]++;
      }
      for (i = 1; i < radix; i++) {
         count[i] = count[i] + count[i - 1];
      }
      for (i = R; i >= L; i--) {
         j = getDigit(arr[i], d);
         help[count[j] - 1] = arr[i];
         count[j]--;
      }
      for (i = L, j = 0; i <= R; i++, j++) {
         arr[i] = help[j];
      }
   }
}


public static int getDigit(int x, int d) {
	return ((x / ((int) Math.pow(10, d - 1))) % 10);
}

P6 链表

1、排序算法稳定性

表现在[0,4,5,1,2,1]中，排完序为[0,1,1,2,4,5]，此时第一个1依然在第二个1之前

选择排序：没有稳定性，是两个数直接进行交换，[3,3,3,3,1,3,3,3,3]，如果使用选择排序，第一个3会和1进行交换

冒泡排序：可以有稳定性，当遍历到相同的时候不交换位置就好了

插入排序：可以有稳定性，当遍历到相同的时候不交换位置就好了

归并排序：可以有稳定性，左边和右边相同时，先添加左边就好了

小和问题：没有稳定性，因为小和问题在数字相同的情况下是需要右边先进行向下操作的

快速排序：没有稳定性，因为是当发现比指定数小时，要和第一个数进行交换，例如：[3,3,3,1,7,5,4]，这里用2做分界值，前3个3不动，到1的时候，需要1和第一个3进行交换

堆排序：没有稳定性，比如[5,4,4,6]，形成大根堆，最开始堆结构：这里第一个4会和6进行交换
在这里插入图片描述

桶排序：一定有稳定性，因为入桶出桶就是按照规则来的，先入先出原则

2、算法总结

在这里插入图片描述

一般选择排序方法时，会选择快速排序，首先它的时间复杂度是最优的，其次它的常数项经过实验的速度是最快的

如果空间有限，很容易空间就超了，使用推排序

如果需要用到稳定性，使用归并排序

**问1：**现在的排序算法能不能做到空间复杂度在O(N * logN)或者以下？

答：不能，目前还没有发现这样的算法

**问2：**现在排序算法能不能同时实现时间复杂度O(N * logN)、空间复杂度O(N)及以下、还有算法稳定性？

答：不能，目前还没有发现这样的算法

时间复杂度和空间复杂度不能够同时拿下

3、常见坑

$[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-y3DISVQc-1681106852040)(C:\Users\卯末\AppData\Roaming\Typora\typora-user-images\image-20230316110005199.png)]$

**（1）**归并排序空间复杂度可以变成O(1)，但何必呢，变成O(1)的同时，会丧失它的稳定性，这样还不如用推排序，复杂度和稳定性都一样，还容易实现

**（2）**原地归并会让空间复杂度变成O(1)，但时间复杂度变O(N^2)，那为什么不用插入呢

**（3）**快排可以稳定，但空间复杂度会变成O(N)，那为什么不用归并呢

**（5）**是一个大坑，就是空间复杂度要求O(1)，时间复杂度要求O(N)，能做到是能做到，但很难，是论文级别算法，面试时就这样回答：经典快排做不到稳定性，但又是01标准（true、false），和奇偶问题一种调整策略，快排做不到，面试官我不清楚怎么做，请你教教我

4、综合排序

就是根据情况选择排序方法，

例子1：大样本量时，使用快速排序，因为时间复杂度O(N * logN)，但当小样本量时，使用的就是插入排序，因为小样本量他的时间复杂度O(N^2)也不会太高

例子2：系统给我们实现的Arrays.sort方法，当它发现你是基础类型，他会给你使用快排，当它发现是自己定义的类型，使用归并，就是出于稳定性的考虑。因为你基础类型稳定性是没用的，会给你使用空间复杂度小的快排，如果你是非基础类型，它不清楚你要不要稳定性，所以使用归并给你稳定性

5、哈希表

哈希表就是key - value，有Hashset（只有key）和HashMap（key和value都有）

哈希表认为增删改查的时间复杂度都是常数级别，比较大的常数

哈希表不是基础类型的保存，是把内存地址拷贝过去，一律都是8字节，和你本身的内存空间没有关系

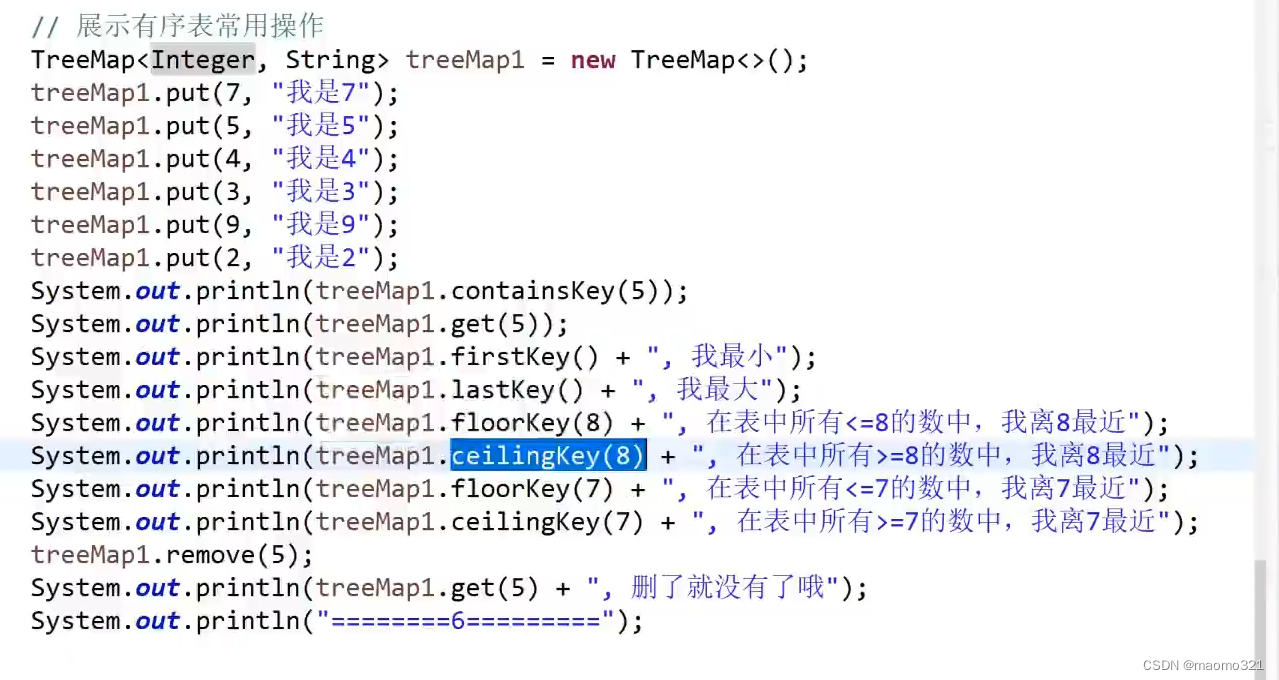
在这里插入图片描述

6、有序表

和哈希表类似，哈希表的key是无序的，有序表则是有序的，哈希表能实现的功能有序表都能够实现，而且由于多

出排序，可以有更多功能

有序表认为增删改查的时间复杂度都是logN级别的

有序表演示代码：

在这里插入图片描述

有序表简单介绍

（第6、7是有序表）

在这里插入图片描述

7、单链表和双链表

定义

单链表：值、一条next指针

双链表：值、一条next指针、一条last指针，分别指向后和前

// 单链表
public static class Node {
   public int value;
   public Node next;
}
// 双链表
public static class Node {
   public int value;
   public Node next;
   public Node last;
}

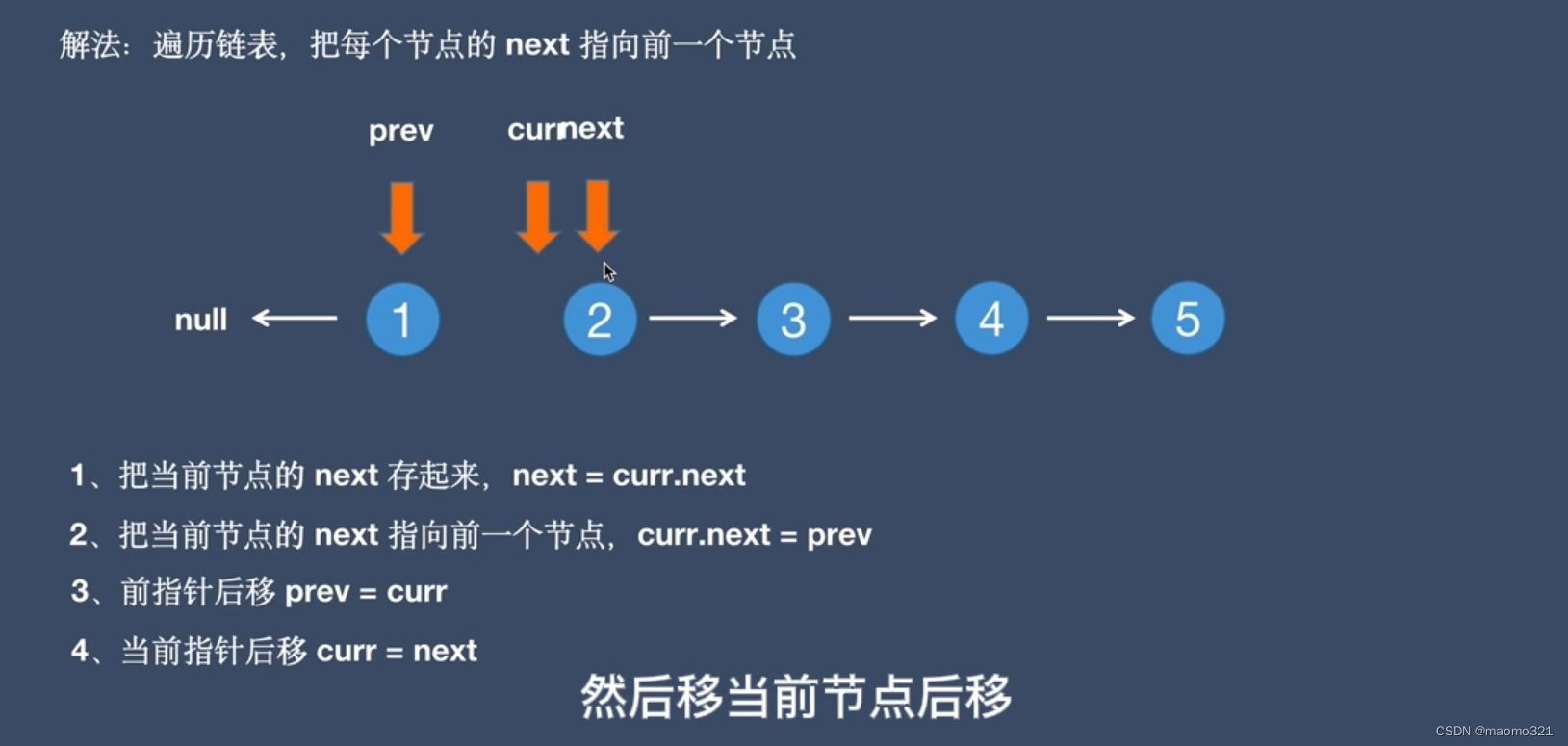
8、链表反转问题

在这里插入图片描述

代码

Node curr = head;
Node prev = null;
Node next = null;
while (curr){
   next = curr.next;
   curr.next = prev;
   prev = curr;
   curr = next;
}

9、链表回文数问题

笔试：

需要用到快慢指针，快指针一次跳2个，慢指针则是1个，当快指针到达终点时，慢指针刚好到中间，这样就能够

知道从哪里开始把链表右边一半存到栈中（从左到右开始存）

面试：

同样是使用快慢指针，但我们不创建额外空间，直接把原来的链表右半段反转，同时把中间数变成null：

1->2->3->2->1 => 1->2->null<-2<-1，两个指针分别从头和尾进行next，一样就同时向下，不一样就弹出，直到有

一个是null，就返回true

// 面试代码
// need O(1) extra space
public static boolean isPalindrome3(Node head) {
   if (head == null || head.next == null) {
      return true;
   }
   Node n1 = head;
   Node n2 = head;
   while (n2.next != null && n2.next.next != null) { // find mid node
      n1 = n1.next; // n1 -> mid
      n2 = n2.next.next; // n2 -> end
   }
   // n1 中点
   
   
   n2 = n1.next; // n2 -> right part first node
   n1.next = null; // mid.next -> null
   Node n3 = null;
   while (n2 != null) { // right part convert
      n3 = n2.next; // n3 -> save next node
      n2.next = n1; // next of right node convert
      n1 = n2; // n1 move
      n2 = n3; // n2 move
   }
   n3 = n1; // n3 -> save last node
   n2 = head;// n2 -> left first node
   boolean res = true;
   while (n1 != null && n2 != null) { // check palindrome
      if (n1.value != n2.value) {
         res = false;
         break;
      }
      n1 = n1.next; // left to mid
      n2 = n2.next; // right to mid
   }
   n1 = n3.next;
   n3.next = null;
   while (n1 != null) { // recover list
      n2 = n1.next;
      n1.next = n3;
      n3 = n1;
      n1 = n2;
   }
   return res;
}

这个问题有很多变式，可能需要快指针跑完，慢指针在中间（偶数个）的前一个数等等

需要自己去多写，不然面试很难搞

10、链表荷兰国旗问题

在这里插入图片描述

笔试：

创建一个Node数组，用来保存链表节点，再使用快速排序算法，将其排列完成之后，再把这几个点串起来即可

代码

public static Node listPartition1(Node head, int pivot) {
   if (head == null) {
      return head;
   }
   Node cur = head;
   int i = 0;
   while (cur != null) {
      i++;
      cur = cur.next;
   }
   Node[] nodeArr = new Node[i];
   i = 0;
   cur = head;
   for (i = 0; i != nodeArr.length; i++) {
      nodeArr[i] = cur;
      cur = cur.next;
   }
   arrPartition(nodeArr, pivot);
   for (i = 1; i != nodeArr.length; i++) {
      nodeArr[i - 1].next = nodeArr[i];
   }
   nodeArr[i - 1].next = null;
   return nodeArr[0];
}

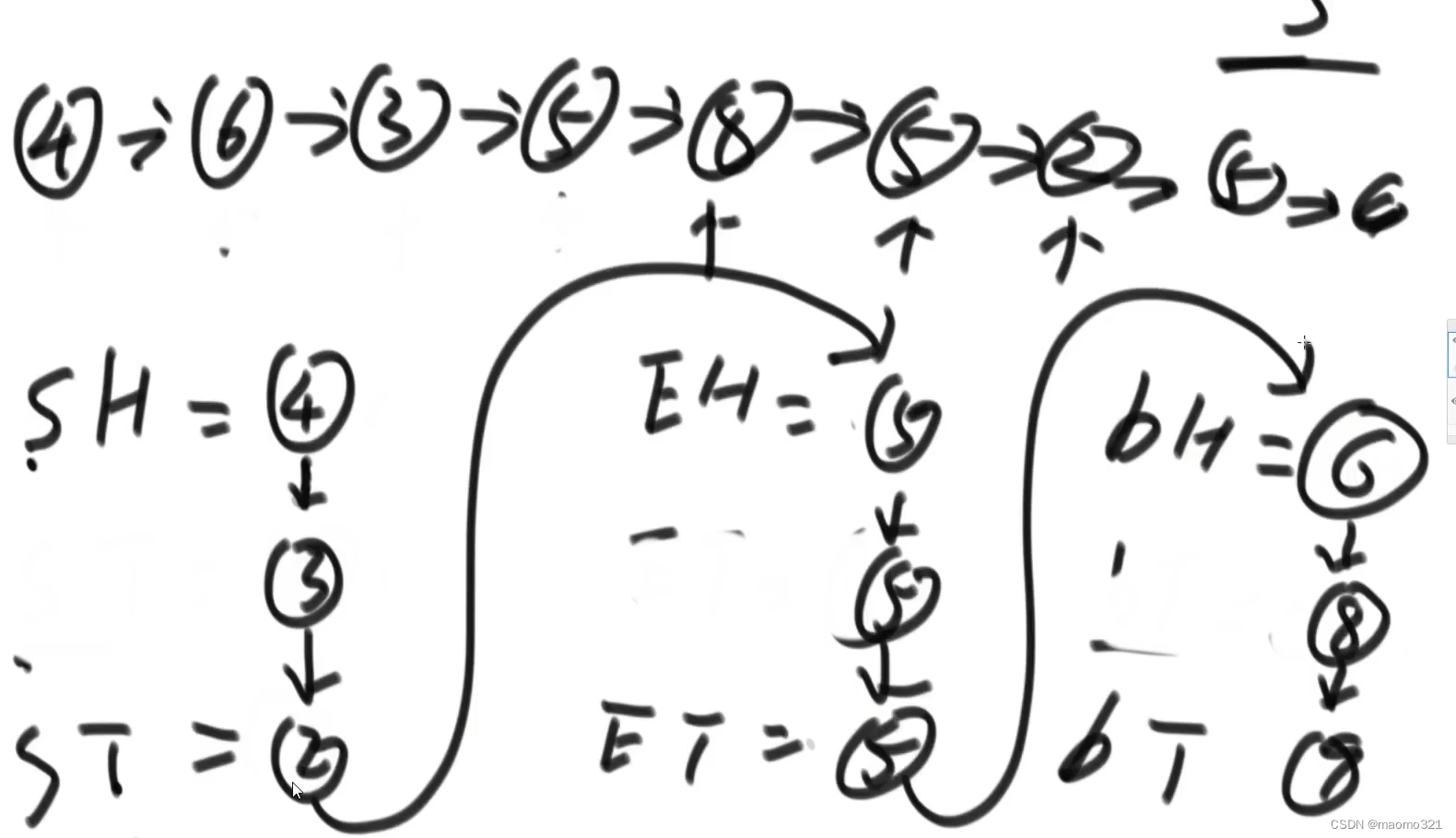
面试：

不能创建额外空间，只需要有六个变量，最开始都指向空，从开头开始查看每个节点，当节点小于规定数值（这里

是5），保存

例如下面，4：由于是刚刚开始，所以SH和ST都是4，

6：同理，BH、BT = 6

3：接到4的下面，SH = 4，ST = 3

5：EH、ET = 5

8：BH = 6，BT = 8

5：略

2：4->3->2

之后再把这3个串接起来即可形成所需要的链表

在这里插入图片描述

代码

public static Node listPartition2(Node head, int pivot) {
   Node sH = null; // small head
   Node sT = null; // small tail
   Node eH = null; // equal head
   Node eT = null; // equal tail
   Node mH = null; // big head
   Node mT = null; // big tail
   Node next = null; // save next node
   // every node distributed to three lists
   while (head != null) {
      next = head.next;
      head.next = null;
      if (head.value < pivot) {
         if (sH == null) {
            sH = head;
            sT = head;
         } else {
            sT.next = head;
            sT = head;
         }
      } else if (head.value == pivot) {
         if (eH == null) {
            eH = head;
            eT = head;
         } else {
            eT.next = head;
            eT = head;
         }
      } else {
         if (mH == null) {
            mH = head;
            mT = head;
         } else {
            mT.next = head;
            mT = head;
         }
      }
      head = next;
   }
   // 小于区域的尾巴，连等于区域的头，等于区域的尾巴连大于区域的头
   if (sT != null) { // 如果有小于区域
      sT.next = eH;
      eT = eT == null ? sT : eT; // 下一步，谁去连大于区域的头，谁就变成eT
   }
   // 下一步，一定是需要用eT 去接 大于区域的头
   // 有等于区域，eT -> 等于区域的尾结点
   // 无等于区域，eT -> 小于区域的尾结点
   // eT 尽量不为空的尾巴节点
   if (eT != null) { // 如果小于区域和等于区域，不是都没有
      eT.next = mH;
   }
   return sH != null ? sH : (eH != null ? eH : mH);
}

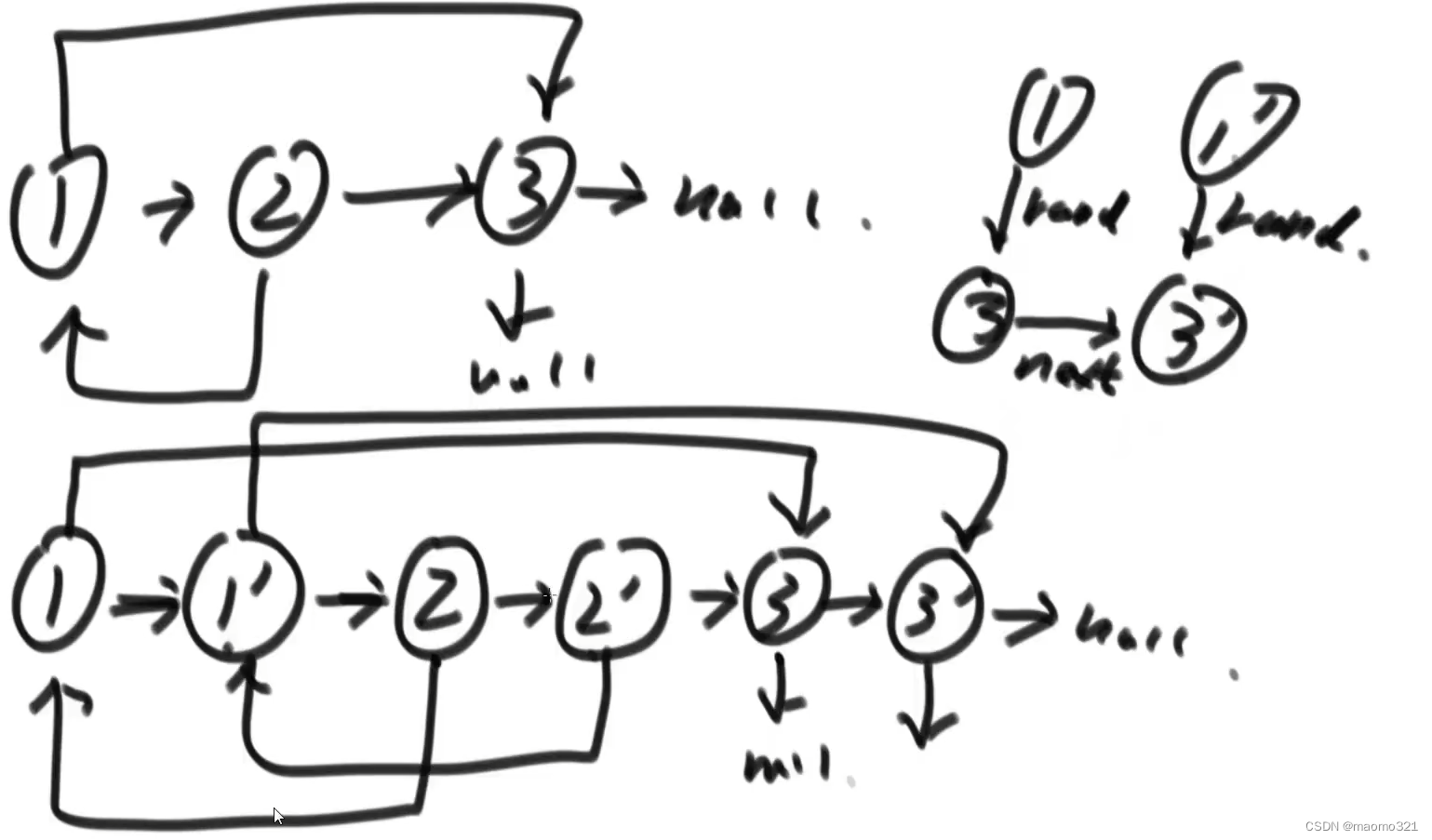
11、复制含有随机指针节点的链表

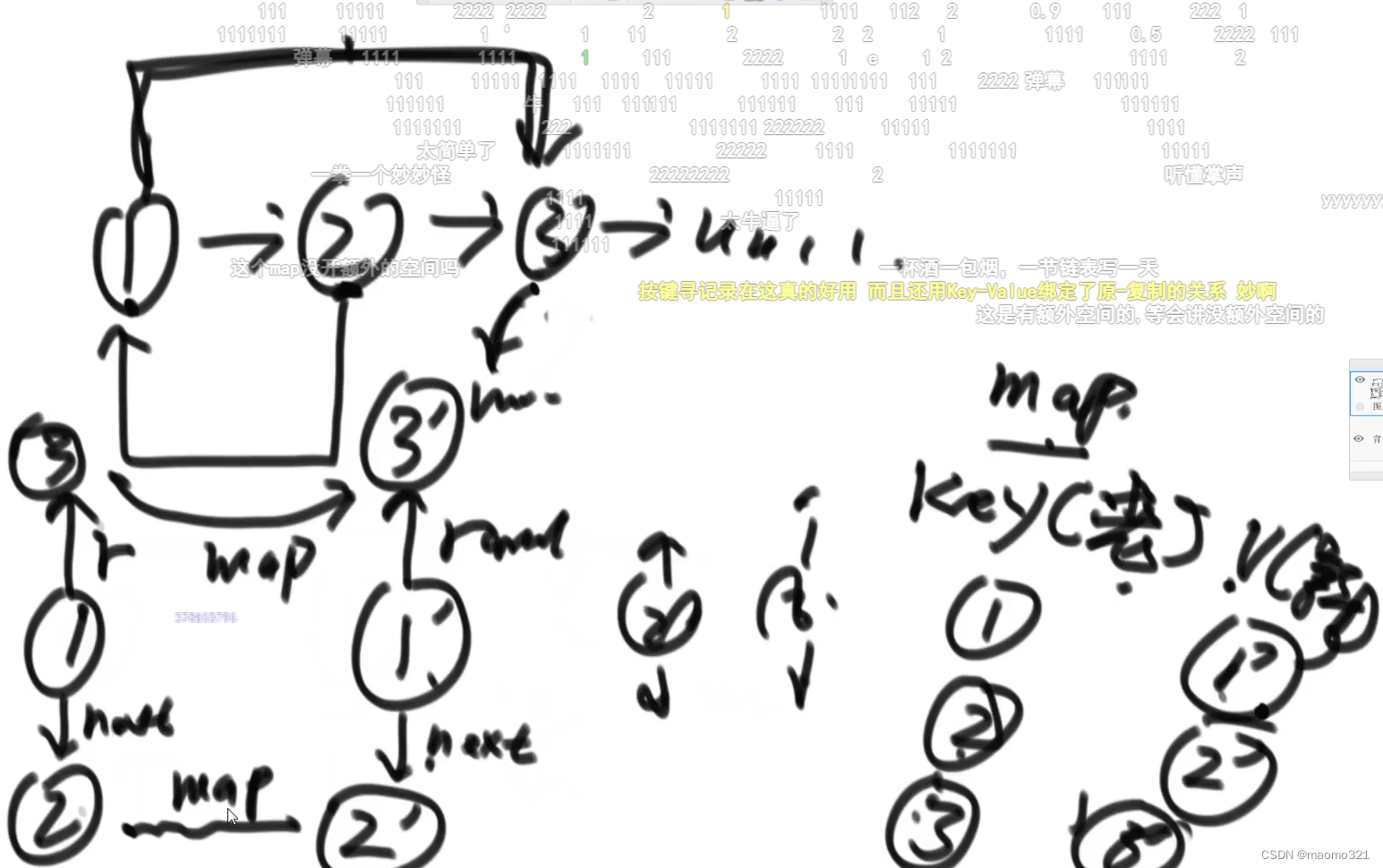
在这里插入图片描述

笔试：

创建额外空间：一个哈希表，key是原来的 1 节点，value是复制过后的 1‘ 节点，因为1节点对应的next是2节点，

2节点对应的value是 2’ 节点，所以 1‘ 节点的next就是 2’ 节点，再用相同的方法查找 1 节点对应的rand：3节点，

3节点再去查找value 3‘ 节点，接在 1’ 节点的rand上，同理进行 2 节点的next 和 rand

在这里插入图片描述

代码

public static Node copyRandomList1(Node head) {
   // key 老节点
   // value 新节点
   HashMap<Node, Node> map = new HashMap<Node, Node>();
   Node cur = head;
   while (cur != null) {
      map.put(cur, new Node(cur.val));
      cur = cur.next;
   }
   cur = head;
   while (cur != null) {
      // cur 老
      // map.get(cur) 新
      // 新.next ->  cur.next克隆节点找到
      map.get(cur).next = map.get(cur.next);
      map.get(cur).random = map.get(cur.random);
      cur = cur.next;
   }
    // 老头部所对应的克隆节点，也就是新结构的头
   return map.get(head);
}

面试：

不使用额外空间，在原链表的节点上进行操作，原节点的next上复制一个新节点，新节点next是原节点的next，

rand不进行设置，之后通过原节点的rand，求出复制节点的rand，例如：1的rand是3，3的复制节点（也就是

next是 3‘ ），这样就让1的复制节点rand指向3的复制节点

在这里插入图片描述

代码

public static Node copyRandomList2(Node head) {
   if (head == null) {
      return null;
   }
   Node cur = head;
   Node next = null;
   // 1 -> 2 -> 3 -> null
   // 1 -> 1' -> 2 -> 2' -> 3 -> 3'
   while (cur != null) {
      next = cur.next;
      cur.next = new Node(cur.val);
      cur.next.next = next;
      cur = next;
   }
   cur = head;
   Node copy = null;
   // 1 1' 2 2' 3 3'
   // 依次设置 1' 2' 3' random指针
   while (cur != null) {
      next = cur.next.next;
      copy = cur.next;
      copy.random = cur.random != null ? cur.random.next : null;
      cur = next;
   }
   Node res = head.next;
   cur = head;
   // 老 新 混在一起，next方向上，random正确
   // next方向上，把新老链表分离
   while (cur != null) {
      next = cur.next.next;
      copy = cur.next;
      cur.next = next;
      copy.next = next != null ? next.next : null;
      cur = next;
   }
   return res;
}

}

面试：

不使用额外空间，在原链表的节点上进行操作，原节点的next上复制一个新节点，新节点next是原节点的next，

rand不进行设置，之后通过原节点的rand，求出复制节点的rand，例如：1的rand是3，3的复制节点（也就是

next是 3‘ ），这样就让1的复制节点rand指向3的复制节点

[外链图片转存中…(img-15IGcOET-1681106852043)]

代码

public static Node copyRandomList2(Node head) {
   if (head == null) {
      return null;
   }
   Node cur = head;
   Node next = null;
   // 1 -> 2 -> 3 -> null
   // 1 -> 1' -> 2 -> 2' -> 3 -> 3'
   while (cur != null) {
      next = cur.next;
      cur.next = new Node(cur.val);
      cur.next.next = next;
      cur = next;
   }
   cur = head;
   Node copy = null;
   // 1 1' 2 2' 3 3'
   // 依次设置 1' 2' 3' random指针
   while (cur != null) {
      next = cur.next.next;
      copy = cur.next;
      copy.random = cur.random != null ? cur.random.next : null;
      cur = next;
   }
   Node res = head.next;
   cur = head;
   // 老 新 混在一起，next方向上，random正确
   // next方向上，把新老链表分离
   while (cur != null) {
      next = cur.next.next;
      copy = cur.next;
      cur.next = next;
      copy.next = next != null ? next.next : null;
      cur = next;
   }
   return res;
}